Azulejos de Girih
Los azulejos Girih son un conjunto de cinco azulejos que se utilizaron en la creación de patrones geométricos islámicos mediante el uso de la técnica de zunchos ( girih ) para la decoración de edificios en la arquitectura islámica . Se han utilizado desde aproximadamente el año 1200 y sus disposiciones experimentaron mejoras significativas a partir delsantuario Darb-i Imam en Isfahán, Irán, construido en 1453.
Cinco fichas
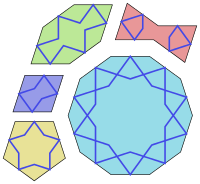
Las cinco formas de las baldosas y sus nombres persas son: [1]
| Nombre | Nombre persa | Número de esquinas | convexo | Especificaciones de ángulo |
|---|---|---|---|---|
| decágono regular | Tabla | 10 | Sí | 144° |
| hexágono alargado (convexo irregular) | Banda Shesh | 6 | Sí | [ 72°, 144°, 144° ] ×2 |
| pajarita (hexágono no convexo) | Sormeh Dan | 6 | No | [ 72°, 72°, 216° ] ×2 |
| rombo | Torán | 4 | Sí | [ 72°, 108° ] ×2 |
| pentágono regular | Pange | 5 | Sí | 108° |
Todos los lados de estas figuras tienen la misma longitud y todos sus ángulos son múltiplos de 36° (π/5 radianes ). Todas ellas, excepto el pentágono, tienen simetría bilateral (de reflexión) a través de dos líneas perpendiculares. Algunas tienen simetrías adicionales. En concreto, el decágono tiene simetría rotacional décuple (rotación de 36°); y el pentágono tiene simetría rotacional quíntuple (rotación de 72°).
La aparición de las baldosas girih
En el siglo XI, los islámicos descubrieron una nueva forma de construir el “mosaico de azulejos” debido al desarrollo del cálculo aritmético y la geometría: los azulejos girih. [2]
Girih
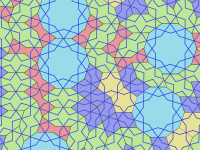
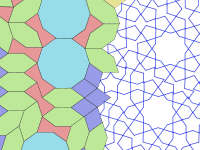
Los girih son líneas ( tiras ) que decoran las baldosas. Las baldosas se utilizan para formar patrones de girih, de la palabra persa گره , que significa "nudo". [3] En la mayoría de los casos, solo son visibles los girih (y otras decoraciones menores como las flores) en lugar de los límites de las baldosas en sí. Los girih son líneas rectas a trozos que cruzan los límites de las baldosas en el centro de un borde a 54° (3π/10 radianes) con respecto al borde. Dos girih que se cruzan cruzan cada borde de una baldosa. La mayoría de las baldosas tienen un patrón único de girih dentro de la baldosa que son continuos y siguen la simetría de la baldosa. Sin embargo, el decágono tiene dos posibles patrones de girih, uno de los cuales tiene solo simetría rotacional quíntuple en lugar de décuple.
Matemáticas de los mosaicos de girih
En 2007, los físicos Peter J. Lu y Paul J. Steinhardt sugirieron que los mosaicos girih poseen propiedades consistentes con mosaicos fractales cuasicristalinos autosimilares como los mosaicos de Penrose , precediéndolos por cinco siglos. [4] [5]
Este hallazgo fue respaldado tanto por el análisis de patrones en las estructuras supervivientes como por el examen de pergaminos persas del siglo XV. No hay ninguna indicación de cuánto más podían saber los arquitectos sobre las matemáticas involucradas. En general, se cree que estos diseños se construyeron trazando contornos en zigzag con solo una regla y un compás. Es posible que se hayan consultado las plantillas encontradas en pergaminos como el Pergamino de Topkapi de 97 pies (29,5 metros) de largo. Encontrado en el Palacio de Topkapi en Estambul, el centro administrativo del Imperio Otomano, y se cree que data de finales del siglo XV, el pergamino muestra una sucesión de patrones geométricos bidimensionales y tridimensionales. No hay texto, pero hay un patrón de cuadrícula y un código de colores utilizado para resaltar las simetrías y distinguir las proyecciones tridimensionales. Dibujos como el que se muestra en este pergamino habrían servido como libros de patrones para los artesanos que fabricaron los azulejos, y las formas de los azulejos girih dictaban cómo podían combinarse en patrones grandes. De esta manera, los artesanos podían realizar diseños altamente complejos sin recurrir a las matemáticas y sin comprender necesariamente sus principios subyacentes. [6]
Este uso de patrones repetidos creados a partir de un número limitado de formas geométricas disponibles para los artesanos de la época es similar a la práctica de los artesanos góticos europeos contemporáneos . Los diseñadores de ambos estilos se preocupaban por utilizar sus inventarios de formas geométricas para crear la máxima diversidad de formas. Esto exigía una habilidad y una práctica muy diferentes de las matemáticas. [6]
Construcción geométrica de un diseño de mosaico de polígonos y decagramas entrelazados
Primero, divide el ángulo recto A en cinco partes del mismo grado creando cuatro rayos que comiencen en A. Encuentra un punto arbitrario C en el segundo rayo y traza perpendiculares desde C a los lados del ángulo A en sentido antihorario. Este paso crea el rectángulo ABCD junto con cuatro segmentos que tienen cada uno un punto final en A; otros puntos finales son las intersecciones de los cuatro rayos con los dos lados de BC y DC del rectángulo ABCD. Luego, encuentra el punto medio del cuarto segmento creado a partir del punto E del cuarto rayo. Construye un arco con centro A y radio AE para intersecar AB en el punto F y el segundo rayo en el punto G. El segundo segmento ahora es parte de la diagonal del rectángulo. Haz una línea paralela a AD y que pase por el punto G que interseque el primer rayo en el punto H y el tercer rayo en el punto I. La línea HF pasa por el punto E e interseca el tercer rayo en L y la línea AD en J. Construye una línea que pase por J que sea paralela al tercer rayo. También se construye la línea EI y se encuentra M, que es la intersección de esta línea con AD. Desde el punto F se traza una línea paralela al tercer rayo para que se cruce con el primer rayo en K. Se construyen los segmentos GK, GL y EM. Se encuentra el punto N tal que GI = IN construyendo un círculo con centro I y radio IG. Se construye la línea DN, que es paralela a GK, para que se cruce con la línea que emana de J, y se encuentra P para completar el pentágono regular EINPJ. La línea DN se cruza con la bisectriz perpendicular de AB en Q. Desde Q se construye una línea paralela a FK para que se cruce con el rayo MI en R. Como se muestra en la figura, utilizando O, que es el centro del rectángulo ABCD, como centro de rotación de 180°, se puede hacer la región fundamental para el mosaico. [1]




Construcción geométrica de un teselado a partir de pergaminos arquitectónicos de Mirza Akbar
En primer lugar, se divide el ángulo recto en cinco ángulos congruentes. Se selecciona un punto arbitrario P en el primer rayo en sentido antihorario. Para el radio del círculo inscrito en el decagramo, se selecciona la mitad del segmento creado a partir del tercer rayo, el segmento AM. La siguiente figura ilustra una solución visual paso a paso con regla y compás para el problema planteada por el autor. [1] Nótese que la forma de dividir un ángulo recto en cinco ángulos congruentes no forma parte de las instrucciones proporcionadas, porque se considera un paso elemental para los diseñadores.

Ejemplos
- Diferentes patrones
- Patrones complejos de estrellas de 16, 10 y 8 puntas en diferentes escalas en el techo de la Tumba de Hafez en Shiraz , 1935
- Una ventana del apartamento del príncipe heredero en el Palacio de Topkapi , Estambul , Turquía, con estrellas de 6 puntas; los alrededores tienen azulejos arabescos florales.
- Arco interior en la apertura de la Logia del Sultán en la Mezquita Verde Otomana en Bursa , Turquía (1424), con estrellas de 10 puntas y pentágonos
El girih se ha aplicado ampliamente en la arquitectura. El girih en las ventanas geométricas persas cumple con los requisitos de la arquitectura persa. Los tipos específicos de adornos utilizados en orosi generalmente vinculaban las ventanas a la eminencia social y política del patrón. Cuanto más ornamentada sea una ventana, mayor será el estatus social y económico del propietario. Un buen ejemplo de esto es Azad Koliji, un jardín de Dowlatabad en Irán [ cita requerida ] . Los patrones girih en su ventana demuestran con éxito múltiples capas. La primera capa sería el jardín real, del cual las personas pueden echar un vistazo cuando abren la ventana. Luego está el primer patrón girih en el exterior de la ventana, el patrón tallado. Otra capa artificial está representada por el vidrio colorido de la ventana, cuyas capas multicolores crean la sensación de una masa de flores. Esta capa abstracta forma una clara contradicción con la capa real fuera de la ventana y da espacio para la imaginación. [7]
Véase también
Referencias
- ^ abc Sarhangi, Reza (2012). "Polígonos estelares entrelazados en la arquitectura persa: el caso especial del decagrama en los diseños de mosaicos". Nexus Netw J . 14 (2). pág. 350. doi :10.1007/s00004-012-0117-5. S2CID 253596464.
- ^ Lu, PJ; Steinhardt, PJ (2007). "Azulejos decagonales y cuasicristalinos en la arquitectura islámica medieval". Science . 315 (5815): 1106–1110. Bibcode :2007Sci...315.1106L. doi :10.1126/science.1135491. JSTOR 20039057. PMID 17322056. S2CID 10374218.
- ^ Sebastian R. Prange (septiembre-octubre de 2009). "The Tiles of Infinity". Saudi Aramco World : 24–31. Archivado desde el original el 13 de enero de 2010. Consultado el 8 de enero de 2010 .
- ^ Peter J. Lu y Paul J. Steinhardt (2007). "Azulejos decagonales y cuasicristalinos en la arquitectura islámica medieval". Science . 315 (5815): 1106–1110. Bibcode :2007Sci...315.1106L. doi :10.1126/science.1135491. PMID 17322056. S2CID 10374218.
- ^ Figuras suplementarias
- ^ ab Gulru Necipoglu (1995). El rollo de Topkapi: geometría y ornamentación en la arquitectura islámica . Getty Research Institute.
- ^ Koliji, Hooman (2015). "Construido sobre la luz: el 'astuto' arte de las ventanas con patrones geométricos". Revista internacional de arquitectura islámica . 4 : 75–108. doi : 10.1007/s00004-016-0288-6 .
Enlaces externos
- Patrones en la arquitectura árabe
- "La arquitectura islámica medieval presagia las matemáticas del siglo XX". Harvard University Gazette. 22 de febrero de 2007. Consultado el 14 de marzo de 2007 .
- "Los mosaicos islámicos medievales revelan conocimientos matemáticos". New Scientist. 22 de febrero de 2007. Consultado el 14 de marzo de 2007 .



