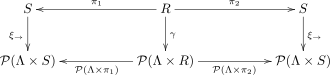Bisimulación

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Bisimulación» – noticias  · periódicos  · libros  · académico  · JSTOR ( febrero de 2017 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En informática teórica una bisimulación es una relación binaria entre sistemas de transición de estados , asociando sistemas que se comportan de la misma manera de modo que un sistema simula al otro y viceversa.

Intuitivamente, dos sistemas son bisimilares si, suponiendo que los consideramos como si jugaran un juego de acuerdo con ciertas reglas, sus movimientos son iguales. En este sentido, un observador no puede distinguir a cada uno de los sistemas del otro.

Dado un sistema de transición de estados etiquetado ( S , Λ, →) , donde S es un conjunto de estados, es un conjunto de etiquetas y → es un conjunto de transiciones etiquetadas (es decir, un subconjunto de ), una bisimulación es una relación binaria , tal que tanto R como su recíproca son simulaciones . De esto se deduce que el cierre simétrico de una bisimulación es una bisimulación, y que cada simulación simétrica es una bisimulación. Por ello, algunos autores definen la bisimulación como una simulación simétrica. ^[1]${\displaystyle \Lambda }$${\displaystyle S\times \Lambda \times S}$ ${\displaystyle R\subseteq S\times S}$ ${\displaystyle R^{T}}$

De manera equivalente, R es una bisimulación si y solo si para cada par de estados en R y todas las etiquetas λ en :${\displaystyle (p,q)}$${\displaystyle \Lambda }$

• si , entonces existe tal que ;${\displaystyle p\mathrel {\overset {\lambda }{\rightarrow }} p'}$${\displaystyle q\mathrel {\overset {\lambda }{\rightarrow }} q'}$${\displaystyle (p',q')\in R}$
• si , entonces existe tal que .${\displaystyle q\mathrel {\overset {\lambda }{\rightarrow }} q'}$${\displaystyle p\mathrel {\overset {\lambda }{\rightarrow }} p'}$${\displaystyle (p',q')\in R}$

Dados dos estados p y q en S , p es bisimilar a q , escrito , si y solo si existe una bisimulación R tal que . Esto significa que la relación de bisimilitud ∼ es la unión de todas las bisimulaciones: precisamente cuando para alguna bisimulación R .${\displaystyle p\,\sim \,q}$${\displaystyle (p,q)\in R}$${\displaystyle (p,q)\in \,\sim \,}$${\displaystyle (p,q)\in R}$

El conjunto de bisimulaciones está cerrado bajo la unión; ^{[Nota 1]} por lo tanto, la relación de bisimilitud es en sí misma una bisimulación. Puesto que es la unión de todas las bisimulaciones, es la única bisimulación más grande. Las bisimulaciones también están cerradas bajo clausura reflexiva, simétrica y transitiva; por lo tanto, la bisimulación más grande debe ser reflexiva, simétrica y transitiva. De esto se sigue que la bisimulación más grande —la bisimilitud— es una relación de equivalencia . ^[2]

La bisimulación se puede definir en términos de composición de relaciones de la siguiente manera.

Dado un sistema de transición de estado etiquetado , una relación de bisimulación es una relación binaria R sobre S (es decir, R ⊆ S × S ) tal que${\displaystyle (S,\Lambda ,\rightarrow )}$ ${\displaystyle \forall \lambda \in \Lambda }$

$${\displaystyle R\ ;\ {\overset {\lambda }{\rightarrow }}\quad {\subseteq }\quad {\overset {\lambda }{\rightarrow }}\ ;\ R}$$y$${\displaystyle R^{-1}\ ;\ {\overset {\lambda }{\rightarrow }}\quad {\subseteq }\quad {\overset {\lambda }{\rightarrow }}\ ;\ R^{-1}}$$

De la monotonía y continuidad de la composición de relaciones se sigue inmediatamente que el conjunto de bisimulaciones está cerrado bajo uniones ( joins en el conjunto de relaciones), y un cálculo algebraico simple muestra que la relación de bisimilaridad (join de todas las bisimulaciones) es una relación de equivalencia. Esta definición, y el tratamiento asociado de la bisimilaridad, se pueden interpretar en cualquier cuanto involutivo .

La bisimilaridad también puede definirse de manera teórica de orden , en términos de la teoría del punto fijo , más precisamente como el mayor punto fijo de una determinada función definida a continuación.

Dado un sistema de transición de estados etiquetado ( , Λ, →), defina como una función de relaciones binarias sobre a relaciones binarias sobre , de la siguiente manera:${\displaystyle S}$${\displaystyle F:{\mathcal {P}}(S\times S)\to {\mathcal {P}}(S\times S)}$${\displaystyle S}$${\displaystyle S}$

Sea cualquier relación binaria sobre . se define como el conjunto de todos los pares en × tales que:${\displaystyle R}$${\displaystyle S}$${\displaystyle F(R)}$${\displaystyle (p,q)}$${\displaystyle S}$${\displaystyle S}$

$${\displaystyle \forall \lambda \in \Lambda .\,\forall p'\in S.\,p{\overset {\lambda }{\rightarrow }}p'\,\Rightarrow \,\exists q'\in S.\,q{\overset {\lambda }{\rightarrow }}q'\,{\textrm {and}}\,(p',q')\in R}$$y$${\displaystyle \forall \lambda \in \Lambda .\,\forall q'\in S.\,q{\overset {\lambda }{\rightarrow }}q'\,\Rightarrow \,\exists p'\in S.\,p{\overset {\lambda }{\rightarrow }}p'\,{\textrm {and}}\,(p',q')\in R}$$

La bisimilaridad se define entonces como el mayor punto fijo de .${\displaystyle F}$

La bisimulación también puede pensarse en términos de un juego entre dos jugadores: atacante y defensor.

El "atacante" va primero y puede elegir cualquier transición válida, , desde . Es decir, o ${\displaystyle \lambda }$${\displaystyle (p,q)}$$${\displaystyle (p,q){\overset {\lambda }{\rightarrow }}(p',q)}$$$${\displaystyle (p,q){\overset {\lambda }{\rightarrow }}(p,q')}$$

El "Defensor" debe entonces intentar igualar esa transición, ya sea desde o desde, dependiendo del movimiento del atacante. Es decir, debe encontrar una manera tal que: o ${\displaystyle \lambda }$${\displaystyle (p',q)}$${\displaystyle (p,q')}$${\displaystyle \lambda }$$${\displaystyle (p',q){\overset {\lambda }{\rightarrow }}(p',q')}$$$${\displaystyle (p,q'){\overset {\lambda }{\rightarrow }}(p',q')}$$

El atacante y el defensor continúan turnándose hasta que:

• El defensor no puede encontrar ninguna transición válida que coincida con el movimiento del atacante. En este caso, el atacante gana.
• El juego llega a estados en los que ambos están "muertos" (es decir, no hay transiciones desde ninguno de los estados). En este caso, el defensor gana.${\displaystyle (p,q)}$
• El juego continúa indefinidamente, en cuyo caso gana el defensor.
• El juego alcanza los estados que ya se han visitado. Esto equivale a una jugada infinita y cuenta como una victoria para el defensor.${\displaystyle (p,q)}$

Según la definición anterior, el sistema es una bisimulación si y sólo si existe una estrategia ganadora para el defensor.

Una bisimulación para sistemas de transición de estados es un caso especial de bisimulación coalgebraica para el tipo de funtor de conjunto potencia covariante . Nótese que cada sistema de transición de estados se puede mapear biyectivamente a una función de al conjunto potencia de indexado por escrito como , definido por${\displaystyle (S,\Lambda ,\rightarrow )}$${\displaystyle \xi _{\rightarrow }}$${\displaystyle S}$${\displaystyle S}$${\displaystyle \Lambda }$${\displaystyle {\mathcal {P}}(\Lambda \times S)}$$${\displaystyle p\mapsto \{(\lambda ,q)\in \Lambda \times S:p{\overset {\lambda }{\rightarrow }}q\}.}$$

Sea -ésima proyección , que se asigna a y respectivamente para ; y la imagen hacia delante de se define eliminando el tercer componente donde es un subconjunto de . De manera similar para .${\displaystyle \pi _{i}\colon S\times S\to S}$${\displaystyle i}$${\displaystyle (p,q)}$${\displaystyle p}$${\displaystyle q}$${\displaystyle i=1,2}$${\displaystyle {\mathcal {P}}(\Lambda \times \pi _{1})}$${\displaystyle \pi _{1}}$$${\displaystyle P\mapsto \{(\lambda ,p)\in \Lambda \times S:\exists q.(\lambda ,p,q)\in P\}}$$${\displaystyle P}$${\displaystyle \Lambda \times S\times S}$${\displaystyle {\mathcal {P}}(\Lambda \times \pi _{2})}$

Usando las notaciones anteriores, una relación es una bisimulación en un sistema de transición si y solo si existe un sistema de transición en la relación tal que el diagrama${\displaystyle R\subseteq S\times S}$${\displaystyle (S,\Lambda ,\rightarrow )}$${\displaystyle \gamma \colon R\to {\mathcal {P}}(\Lambda \times R)}$${\displaystyle R}$

conmuta, es decir, para , las ecuaciones se cumplen donde es la representación funcional de .${\displaystyle i=1,2}$$${\displaystyle \xi _{\rightarrow }\circ \pi _{i}={\mathcal {P}}(\Lambda \times \pi _{i})\circ \gamma }$$${\displaystyle \xi _{\rightarrow }}$${\displaystyle (S,\Lambda ,\rightarrow )}$

En contextos especiales, la noción de bisimulación a veces se perfecciona añadiendo requisitos o restricciones adicionales. Un ejemplo es el de la bisimulación de tartamudeo , en la que una transición de un sistema puede coincidir con múltiples transiciones del otro, siempre que los estados intermedios sean equivalentes al estado inicial ("tartamudea"). ^[3]

Una variante diferente se aplica si el sistema de transición de estados incluye una noción de acción silenciosa (o interna ), a menudo denotada con , es decir, acciones que no son visibles para los observadores externos, entonces la bisimulación se puede relajar para ser bisimulación débil , en la que si dos estados y son bisimilares y hay algún número de acciones internas que conducen desde a algún estado , entonces debe existir un estado tal que haya algún número (posiblemente cero) de acciones internas que conducen desde a . Una relación sobre procesos es una bisimulación débil si se cumple lo siguiente (siendo , y una transición observable y muda respectivamente):${\displaystyle \tau }$${\displaystyle p}$${\displaystyle q}$${\displaystyle p}$${\displaystyle p'}$${\displaystyle q'}$${\displaystyle q}$${\displaystyle q'}$${\displaystyle {\mathcal {R}}}$${\displaystyle {\mathcal {S}}\in \{{\mathcal {R}},{\mathcal {R}}^{-1}\}}$${\displaystyle a,\tau }$

$${\displaystyle \forall p,q.\quad (p,q)\in {\mathcal {S}}\Rightarrow p{\stackrel {\tau }{\rightarrow }}p'\Rightarrow \exists q'.\quad q{\stackrel {\tau ^{\ast }}{\rightarrow }}q'\wedge (p',q')\in {\mathcal {S}}}$$$${\displaystyle \forall p,q.\quad (p,q)\in {\mathcal {S}}\Rightarrow p{\stackrel {a}{\rightarrow }}p'\Rightarrow \exists q'.\quad q{\stackrel {\tau ^{\ast }a\tau ^{\ast }}{\rightarrow }}q'\wedge (p',q')\in {\mathcal {S}}}$$

Esto está estrechamente relacionado ^{[ ¿cómo? ]} con la noción de bisimulación " hasta " una relación. ^[4]

Por lo general, si el sistema de transición de estados proporciona la semántica operacional de un lenguaje de programación , entonces la definición precisa de bisimulación será específica de las restricciones del lenguaje de programación. Por lo tanto, en general, puede haber más de un tipo de relación de bisimulación (o bisimilaridad) según el contexto.

Dado que los modelos de Kripke son un caso especial de sistemas de transición de estados (etiquetados), la bisimulación también es un tema de la lógica modal . De hecho, la lógica modal es el fragmento de la lógica de primer orden invariante bajo la bisimulación ( teorema de van Benthem ).

La comprobación de que dos sistemas de transición finitos son bisimilares se puede realizar en tiempo polinomial . ^[5] Los algoritmos más rápidos son los de tiempo cuasilineal que utilizan refinamiento de partición a través de una reducción al problema de partición más burdo.

• Pedido anticipado de simulación
• Relación de congruencia
• Bisimulación probabilística

• Park, David (1981). "Concurrencia y autómatas en secuencias infinitas". En Deussen, Peter (ed.). Ciencias de la computación teórica . Actas de la quinta conferencia GI, Karlsruhe. Apuntes de clase en ciencias de la computación . Vol. 104. Springer-Verlag . págs. 167–183. doi :10.1007/BFb0017309. ISBN. 978-3-540-10576-3.
• Milner, Robin (1989). Comunicación y concurrencia . Prentice Hall . ISBN. 0-13-114984-9.
• Sangiorgi, Davide (2011). Introducción a la bisimulación y la coinducción. Cambridge, Reino Unido: Cambridge University Press. ISBN 9781107003637.OCLC 773040572  .

• CADP : herramientas para minimizar y comparar sistemas de estados finitos según varias bisimulaciones
• mCRL2 : herramientas para minimizar y comparar sistemas de estados finitos según varias bisimulaciones
• El juego de la bisimulación