Línea de transmisión

En ingeniería eléctrica , una línea de transmisión es un cable especializado u otra estructura diseñada para conducir ondas electromagnéticas de manera contenida. El término se aplica cuando los conductores son lo suficientemente largos como para que se deba tener en cuenta la naturaleza ondulatoria de la transmisión. Esto se aplica especialmente a la ingeniería de radiofrecuencia porque las longitudes de onda cortas significan que los fenómenos de onda surgen en distancias muy cortas (que pueden ser tan cortas como milímetros dependiendo de la frecuencia). Sin embargo, la teoría de las líneas de transmisión se desarrolló históricamente para explicar los fenómenos en líneas telegráficas muy largas, especialmente los cables telegráficos submarinos .

Las líneas de transmisión se utilizan para fines tales como conectar transmisores y receptores de radio con sus antenas (entonces se denominan líneas de alimentación o alimentadores), distribuir señales de televisión por cable , líneas troncales que enrutan llamadas entre centros de conmutación telefónica, conexiones de redes informáticas y buses de datos informáticos de alta velocidad . Los ingenieros de RF suelen utilizar trozos cortos de línea de transmisión, normalmente en forma de líneas de transmisión planas impresas , dispuestas en ciertos patrones para construir circuitos como filtros . Estos circuitos, conocidos como circuitos de elementos distribuidos , son una alternativa a los circuitos tradicionales que utilizan condensadores e inductores discretos .

Los cables eléctricos ordinarios son suficientes para transportar corriente alterna (CA) de baja frecuencia, como la red eléctrica , que invierte la dirección de 100 a 120 veces por segundo, y señales de audio . Sin embargo, generalmente no se utilizan para transportar corrientes en el rango de radiofrecuencia , ^[1] por encima de aproximadamente 30 kHz, porque la energía tiende a irradiarse desde el cable como ondas de radio , lo que causa pérdidas de potencia. Las corrientes de radiofrecuencia también tienden a reflejarse desde discontinuidades en el cable, como conectores y uniones, y viajan de regreso por el cable hacia la fuente. ^{[1] [2]} Estas reflexiones actúan como cuellos de botella, evitando que la potencia de la señal llegue al destino. Las líneas de transmisión utilizan una construcción especializada y adaptación de impedancia para transportar señales electromagnéticas con reflexiones y pérdidas de potencia mínimas. La característica distintiva de la mayoría de las líneas de transmisión es que tienen dimensiones de sección transversal uniformes a lo largo de su longitud, lo que les da una impedancia uniforme , llamada impedancia característica , ^{[2] [3] [4]} para evitar reflexiones. Los tipos de líneas de transmisión incluyen líneas paralelas ( líneas en escalera , par trenzado ), cables coaxiales y líneas de transmisión planas como stripline y microstrip . ^{[5] [6]} Cuanto mayor sea la frecuencia de las ondas electromagnéticas que se mueven a través de un cable o medio determinado, más corta será la longitud de onda de las ondas. Las líneas de transmisión se vuelven necesarias cuando la longitud de onda de la frecuencia transmitida es lo suficientemente corta como para que la longitud del cable se convierta en una parte significativa de una longitud de onda.

A frecuencias de microondas y superiores, las pérdidas de potencia en las líneas de transmisión se vuelven excesivas y en su lugar se utilizan guías de ondas ^[1], que funcionan como "tuberías" para confinar y guiar las ondas electromagnéticas. ^[6] Algunas fuentes definen las guías de ondas como un tipo de línea de transmisión; ^[6] sin embargo, este artículo no las incluirá.

El análisis matemático del comportamiento de las líneas de transmisión eléctrica surgió del trabajo de James Clerk Maxwell , Lord Kelvin y Oliver Heaviside . En 1855, Lord Kelvin formuló un modelo de difusión de la corriente en un cable submarino. El modelo predijo correctamente el mal rendimiento del cable telegráfico submarino transatlántico de 1858. En 1885, Heaviside publicó los primeros artículos que describían su análisis de la propagación en cables y la forma moderna de las ecuaciones del telegrafista . ^[7]

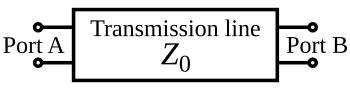
Para fines de análisis, una línea de transmisión eléctrica se puede modelar como una red de dos puertos (también llamada cuadripolo), de la siguiente manera:

En el caso más simple, se supone que la red es lineal (es decir, el voltaje complejo a través de cada puerto es proporcional a la corriente compleja que fluye hacia él cuando no hay reflexiones), y se supone que los dos puertos son intercambiables. Si la línea de transmisión es uniforme a lo largo de su longitud, entonces su comportamiento se describe en gran medida por dos parámetros llamados impedancia característica , símbolo Z ₀ y retardo de propagación , símbolo . Z ₀ es la relación entre el voltaje complejo de una onda dada y la corriente compleja de la misma onda en cualquier punto de la línea. Los valores típicos de Z ₀ son 50 o 75 ohmios para un cable coaxial , aproximadamente 100 ohmios para un par trenzado de cables y aproximadamente 300 ohmios para un tipo común de par no trenzado utilizado en la transmisión de radio. El retardo de propagación es proporcional a la longitud de la línea de transmisión y nunca es menor que la longitud dividida por la velocidad de la luz . Los retrasos típicos para las líneas de transmisión de comunicaciones modernas varían de${\displaystyle \tau_{p}}$3,33 ns/m a5ns/m .

Cuando se envía energía a través de una línea de transmisión, generalmente es deseable que la carga absorba la mayor cantidad posible de energía y que la menor cantidad posible se refleje de regreso a la fuente. Esto se puede garantizar haciendo que la impedancia de carga sea igual a Z ₀ , en cuyo caso se dice que la línea de transmisión está acoplada .

Parte de la potencia que se suministra a una línea de transmisión se pierde debido a su resistencia. Este efecto se denomina pérdida óhmica o resistiva (véase calentamiento óhmico ). A altas frecuencias, otro efecto llamado pérdida dieléctrica se vuelve significativo, sumándose a las pérdidas causadas por la resistencia. La pérdida dieléctrica se produce cuando el material aislante dentro de la línea de transmisión absorbe energía del campo eléctrico alterno y la convierte en calor (véase calentamiento dieléctrico ). La línea de transmisión se modela con una resistencia (R) y una inductancia (L) en serie con una capacitancia (C) y una conductancia (G) en paralelo. La resistencia y la conductancia contribuyen a la pérdida en una línea de transmisión.

La pérdida total de potencia en una línea de transmisión suele especificarse en decibelios por metro (dB/m) y suele depender de la frecuencia de la señal. El fabricante suele proporcionar un gráfico que muestra la pérdida en dB/m en un rango de frecuencias. Una pérdida de 3 dB corresponde aproximadamente a la mitad de la potencia.

El retardo de propagación suele especificarse en unidades de nanosegundos por metro. Si bien el retardo de propagación suele depender de la frecuencia de la señal, las líneas de transmisión suelen funcionar en rangos de frecuencia en los que el retardo de propagación es aproximadamente constante.

Las ecuaciones del telégrafo (o simplemente ecuaciones del telégrafo ) son un par de ecuaciones diferenciales lineales que describen el voltaje ( ) y la corriente ( ) en una línea de transmisión eléctrica con la distancia y el tiempo. Fueron desarrolladas por Oliver Heaviside , quien creó el modelo de línea de transmisión , y se basan en las ecuaciones de Maxwell .${\estilo de visualización V}$${\displaystyle I}$

El modelo de línea de transmisión es un ejemplo del modelo de elementos distribuidos . Representa la línea de transmisión como una serie infinita de componentes elementales de dos puertos, cada uno de los cuales representa un segmento infinitesimalmente corto de la línea de transmisión:

• La resistencia distribuida de los conductores está representada por una resistencia en serie (expresada en ohmios por unidad de longitud).${\estilo de visualización R}$
• La inductancia distribuida (debida al campo magnético alrededor de los cables, autoinducción , etc.) está representada por un inductor en serie (en henries por unidad de longitud).${\estilo de visualización L}$
• La capacitancia entre los dos conductores está representada por un condensador shunt (en faradios por unidad de longitud).${\estilo de visualización C}$
• La conductancia del material dieléctrico que separa los dos conductores está representada por una resistencia de derivación entre el cable de señal y el cable de retorno (en siemens por unidad de longitud).${\estilo de visualización G}$

El modelo consta de una serie infinita de los elementos que se muestran en la figura, y los valores de los componentes se especifican por unidad de longitud, por lo que la imagen del componente puede ser engañosa. , , , y también pueden ser funciones de frecuencia. Una notación alternativa es utilizar , , y para enfatizar que los valores son derivados con respecto a la longitud. Estas cantidades también se pueden conocer como las constantes de línea primarias para distinguirlas de las constantes de línea secundarias derivadas de ellas, siendo estas la constante de propagación , la constante de atenuación y la constante de fase .${\estilo de visualización R}$${\estilo de visualización L}$${\estilo de visualización C}$${\estilo de visualización G}$${\estilo de visualización R'}$${\estilo de visualización L'}$${\estilo de visualización C'}$${\estilo de visualización G'}$

El voltaje de línea y la corriente se pueden expresar en el dominio de la frecuencia como${\estilo de visualización V(x)}$${\displaystyle I(x)}$

${\displaystyle {\frac {\parcial V(x)}{\parcial x}}=-(R+j\,\omega \,L)\,I(x)}$

${\displaystyle {\frac {\parcial I(x)}{\parcial x}}=-(G+j\,\omega \,C)\,V(x)~\,.}$

(ver ecuación diferencial , frecuencia angular ω y unidad imaginaria j )

Cuando los elementos y son despreciablemente pequeños, la línea de transmisión se considera una estructura sin pérdidas. En este caso hipotético, el modelo depende únicamente de los elementos y, lo que simplifica enormemente el análisis. Para una línea de transmisión sin pérdidas, las ecuaciones de Telegrapher de estado estable de segundo orden son:${\estilo de visualización R}$${\estilo de visualización G}$${\estilo de visualización L}$${\estilo de visualización C}$

${\displaystyle {\frac {\parcial ^{2}V(x)}{\parcial x^{2}}}+\omega ^{2}L\,C\,V(x)=0}$

${\displaystyle {\frac {\parcial ^{2}I(x)}{\parcial x^{2}}}+\omega ^{2}L\,C\,I(x)=0~\,.}$

Se trata de ecuaciones de onda que tienen como solución ondas planas con la misma velocidad de propagación en las direcciones de avance y retroceso. El significado físico de esto es que las ondas electromagnéticas se propagan por las líneas de transmisión y, en general, hay un componente reflejado que interfiere con la señal original. Estas ecuaciones son fundamentales para la teoría de líneas de transmisión.

En el caso general, se incluyen los términos de pérdida, y , y la forma completa de las ecuaciones del Telegrapher se convierte en:${\estilo de visualización R}$${\estilo de visualización G}$

${\displaystyle {\frac {\parcial ^{2}V(x)}{\parcial x^{2}}}=\gamma ^{2}V(x)\,}$

${\displaystyle {\frac {\partial ^{2}I(x)}{\partial x^{2}}}=\gamma ^{2}I(x)\,}$

donde es la constante de propagación ( compleja ) . Estas ecuaciones son fundamentales para la teoría de líneas de transmisión. También son ecuaciones de onda y tienen soluciones similares al caso especial, pero que son una mezcla de senos y cosenos con factores de decaimiento exponencial. Al resolver la constante de propagación en términos de los parámetros primarios , , y se obtiene:${\displaystyle \gamma }$${\displaystyle \gamma }$${\displaystyle R}$${\displaystyle L}$${\displaystyle G}$${\displaystyle C}$

${\displaystyle \gamma ={\sqrt {(R+j\,\omega \,L)(G+j\,\omega \,C)\,}}}$

y la impedancia característica se puede expresar como

${\displaystyle Z_{0}={\sqrt {{\frac {R+j\,\omega \,L}{G+j\,\omega \,C}}\,}}~\,.}$

Las soluciones para y son:${\displaystyle V(x)}$${\displaystyle I(x)}$

${\displaystyle V(x)=V_{(+)}e^{-\gamma \,x}+V_{(-)}e^{+\gamma \,x}\,}$

${\displaystyle I(x)={\frac {1}{Z_{0}}}\,\left(V_{(+)}e^{-\gamma \,x}-V_{(-)}e^{+\gamma \,x}\right)~\,.}$

Las constantes deben determinarse a partir de las condiciones de contorno. Para un pulso de voltaje , que comienza en y se mueve en la  dirección positiva, entonces el pulso transmitido en la posición se puede obtener calculando la Transformada de Fourier, , de , atenuando cada componente de frecuencia en , adelantando su fase en , y tomando la Transformada de Fourier inversa . Las partes real e imaginaria de se pueden calcular como${\displaystyle V_{(\pm )}}$${\displaystyle V_{\mathrm {in} }(t)\,}$${\displaystyle x=0}$${\displaystyle x}$${\displaystyle V_{\mathrm {out} }(x,t)\,}$${\displaystyle x}$${\displaystyle {\tilde {V}}(\omega )}$${\displaystyle V_{\mathrm {in} }(t)\,}$${\displaystyle e^{-\operatorname {Re} (\gamma )\,x}\,}$${\displaystyle -\operatorname {Im} (\gamma )\,x\,}$${\displaystyle \gamma }$

${\displaystyle \operatorname {Re} (\gamma )=\alpha =(a^{2}+b^{2})^{1/4}\cos(\psi )\,}$

${\displaystyle \operatorname {Im} (\gamma )=\beta =(a^{2}+b^{2})^{1/4}\sin(\psi )\,}$

con

${\displaystyle a~\equiv ~R\,G\,-\omega ^{2}L\,C\ ~=~\omega ^{2}L\,C\,\left[\left({\frac {R}{\omega L}}\right)\left({\frac {G}{\omega C}}\right)-1\right]}$

${\displaystyle b~\equiv ~\omega \,C\,R+\omega \,L\,G~=~\omega ^{2}L\,C\,\left({\frac {R}{\omega \,L}}+{\frac {G}{\omega \,C}}\right)}$

las expresiones de la derecha se cumplen cuando ni , ni , ni es cero, y con${\displaystyle L}$${\displaystyle C}$${\displaystyle \omega }$

${\displaystyle \psi ~\equiv ~{\tfrac {1}{2}}\operatorname {atan2} (b,a)\,}$

donde atan2 es la forma definida en todas partes de la función arcotangente de dos parámetros, con valor arbitrario cero cuando ambos argumentos son cero.

Alternativamente, la raíz cuadrada compleja se puede evaluar algebraicamente, para obtener:

${\displaystyle \alpha ={\frac {\pm b}{\sqrt {2\left(-a+{\sqrt {a^{2}+b^{2}}}\right)~}}},}$

y

${\displaystyle \beta =\pm {\sqrt {{\tfrac {1}{2}}\left(-a+{\sqrt {a^{2}+b^{2}}}\right)~}},}$

con los signos más o menos elegidos opuestos a la dirección del movimiento de la onda a través del medio conductor. ( a es usualmente negativo, ya que y son típicamente mucho más pequeños que y , respectivamente, por lo que −a es usualmente positivo. b siempre es positivo.)${\displaystyle G}$${\displaystyle R}$${\displaystyle \omega C}$${\displaystyle \omega L}$

Para pequeñas pérdidas y altas frecuencias, las ecuaciones generales se pueden simplificar: Si y entonces${\displaystyle {\tfrac {R}{\omega \,L}}\ll 1}$${\displaystyle {\tfrac {G}{\omega \,C}}\ll 1}$

${\displaystyle \operatorname {Re} (\gamma )=\alpha \approx {\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,}$

${\displaystyle \operatorname {Im} (\gamma )=\beta \approx \omega \,{\sqrt {L\,C\,}}~.\,}$

Dado que un avance de fase de es equivalente a un retraso de tiempo de , se puede calcular simplemente como${\displaystyle -\omega \,\delta }$${\displaystyle \delta }$${\displaystyle V_{out}(t)}$

${\displaystyle V_{\mathrm {out} }(x,t)\approx V_{\mathrm {in} }(t-{\sqrt {L\,C\,}}\,x)\,e^{-{\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,x}.\,}$

La condición de Heaviside es . ${\displaystyle {\frac {G}{C}}={\frac {R}{L}}}$

Si R, G, L y C son constantes que no dependen de la frecuencia y se cumple la condición de Heaviside, entonces las ondas viajan por la línea de transmisión sin distorsión de dispersión .

La impedancia característica de una línea de transmisión es la relación entre la amplitud de una onda de tensión y su onda de corriente. Dado que la mayoría de las líneas de transmisión también tienen una onda reflejada, la impedancia característica no suele ser la impedancia que se mide en la línea.${\displaystyle Z_{0}}$

La impedancia medida a una distancia dada de la impedancia de carga puede expresarse como${\displaystyle \ell }$${\displaystyle Z_{\mathrm {L} }}$

${\displaystyle Z_{\mathrm {in} }\left(\ell \right)={\frac {V(\ell )}{I(\ell )}}=Z_{0}{\frac {1+{\mathit {\Gamma }}_{\mathrm {L} }e^{-2\gamma \ell }}{1-{\mathit {\Gamma }}_{\mathrm {L} }e^{-2\gamma \ell }}}}$,

donde es la constante de propagación y es el coeficiente de reflexión de voltaje medido en el extremo de carga de la línea de transmisión. Alternativamente, la fórmula anterior se puede reorganizar para expresar la impedancia de entrada en términos de la impedancia de carga en lugar del coeficiente de reflexión de voltaje de carga:${\displaystyle \gamma }$${\displaystyle {\mathit {\Gamma }}_{\mathrm {L} }={\frac {\,Z_{\mathrm {L} }-Z_{0}\,}{Z_{\mathrm {L} }+Z_{0}}}}$

${\displaystyle Z_{\mathrm {in} }(\ell )=Z_{0}\,{\frac {Z_{\mathrm {L} }+Z_{0}\tanh \left(\gamma \ell \right)}{Z_{0}+Z_{\mathrm {L} }\,\tanh \left(\gamma \ell \right)}}}$.

Para una línea de transmisión sin pérdidas, la constante de propagación es puramente imaginaria, por lo que las fórmulas anteriores se pueden reescribir como${\displaystyle \gamma =j\,\beta }$

${\displaystyle Z_{\mathrm {in} }(\ell )=Z_{0}{\frac {Z_{\mathrm {L} }+j\,Z_{0}\,\tan(\beta \ell )}{Z_{0}+j\,Z_{\mathrm {L} }\tan(\beta \ell )}}}$

¿Dónde está el número de onda ?${\displaystyle \beta ={\frac {\,2\pi \,}{\lambda }}}$

En el cálculo, la longitud de onda suele ser diferente dentro de la línea de transmisión de lo que sería en el espacio libre. Por lo tanto, al realizar dicho cálculo, se debe tener en cuenta el factor de velocidad del material del que está hecha la línea de transmisión.${\displaystyle \beta ,}$

Para el caso especial donde n es un entero (lo que significa que la longitud de la línea es un múltiplo de la mitad de una longitud de onda), la expresión se reduce a la impedancia de carga de modo que${\displaystyle \beta \,\ell =n\,\pi }$

${\displaystyle Z_{\mathrm {in} }=Z_{\mathrm {L} }\,}$

para todos Esto incluye el caso en el que , lo que significa que la longitud de la línea de transmisión es insignificantemente pequeña en comparación con la longitud de onda. El significado físico de esto es que la línea de transmisión se puede ignorar (es decir, tratar como un cable) en cualquier caso.${\displaystyle n\,.}$${\displaystyle n=0}$

Para el caso en que la longitud de la línea es un cuarto de longitud de onda, o un múltiplo impar de un cuarto de longitud de onda, la impedancia de entrada se convierte en

${\displaystyle Z_{\mathrm {in} }={\frac {Z_{0}^{2}}{Z_{\mathrm {L} }}}~\,.}$

Otro caso especial es cuando la impedancia de carga es igual a la impedancia característica de la línea (es decir, la línea está adaptada ), en cuyo caso la impedancia se reduce a la impedancia característica de la línea de modo que

${\displaystyle Z_{\mathrm {in} }=Z_{\mathrm {L} }=Z_{0}\,}$

para todos y todas .${\displaystyle \ell }$${\displaystyle \lambda }$

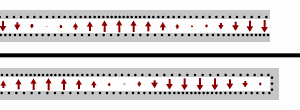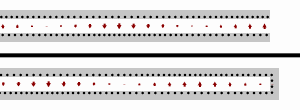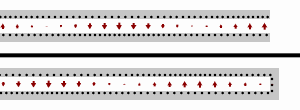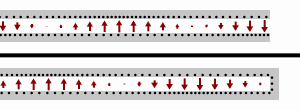
Para el caso de una carga en cortocircuito (es decir, ), la impedancia de entrada es puramente imaginaria y una función periódica de la posición y la longitud de onda (frecuencia).${\displaystyle Z_{\mathrm {L} }=0}$

${\displaystyle Z_{\mathrm {in} }(\ell )=j\,Z_{0}\,\tan(\beta \ell ).\,}$

Para el caso de una carga abierta (es decir, ), la impedancia de entrada es nuevamente imaginaria y periódica.${\displaystyle Z_{\mathrm {L} }=\infty }$

${\displaystyle Z_{\mathrm {in} }(\ell )=-j\,Z_{0}\cot(\beta \ell ).\,}$

La simulación de líneas de transmisión integradas en sistemas más grandes generalmente utiliza parámetros de admitancia (matriz Y), parámetros de impedancia (matriz Z) y/o parámetros de dispersión (matriz S) que incorporan el modelo de línea de transmisión completo necesario para respaldar la simulación.

Los parámetros de admitancia (Y) se pueden definir aplicando un voltaje fijo a un puerto (V1) de una línea de transmisión con el otro extremo en cortocircuito a tierra y midiendo la corriente resultante que fluye hacia cada puerto (I1, I2) ^{[8] [9]} y calculando la admitancia en cada puerto como una relación de I/V El parámetro de admitancia Y11 es I1/V1, y el parámetro de admitancia Y12 es I2/V1. Dado que las líneas de transmisión son dispositivos eléctricamente pasivos y simétricos, Y12 = Y21, e Y11 = Y22.

Para líneas de transmisión con y sin pérdidas respectivamente, la matriz de parámetros Y es la siguiente: ^{[10] [11]}

${\displaystyle Y_{\text{Lossless}}={\begin{bmatrix}{\frac {-jcot(\beta l)}{Z_{o}}}&{\frac {jcsc(\beta l)}{Z_{o}}}\\{\frac {jcsc(\beta l)}{Z_{o}}}&{\frac {-jcot(\beta l)}{Z_{o}}}\end{bmatrix}}{\text{ }}Y_{\text{Lossy}}={\begin{bmatrix}{\frac {coth(\gamma l)}{Z_{o}}}&{\frac {-csch(\gamma l)}{Z_{o}}}\\{\frac {-csch(\gamma l)}{Z_{o}}}&{\frac {coth(\gamma l)}{Z_{o}}}\end{bmatrix}}}$

El parámetro de impedancia (Z) se puede definir aplicando una corriente fija en un puerto (I1) de una línea de transmisión con el otro puerto abierto y midiendo el voltaje resultante en cada puerto (V1, V2) ^{[8] [9]} y calculando el parámetro de impedancia Z11 como V1/I1, y el parámetro de impedancia Z12 como V2/I1. Dado que las líneas de transmisión son dispositivos eléctricamente pasivos y simétricos, V12 = V21 y V11 = V22.

En las definiciones de matrices Y y Z, y . ^[12] A diferencia de los elementos ideales de 2 puertos concentrados ( resistencias , capacitores , inductores , etc.) que no tienen parámetros Z definidos, las líneas de transmisión tienen una ruta interna a tierra, que permite la definición de parámetros Z.${\displaystyle Y=Z^{-1}}$${\displaystyle Z=Y^{-1}}$

Para líneas de transmisión con y sin pérdidas respectivamente, la matriz de parámetros Z es la siguiente: ^{[10] [11]}

${\displaystyle Z_{\text{Lossless}}={\begin{bmatrix}-jZ_{o}cot(\beta l)&-jZ_{o}csc(\beta l)\\-jZ_{o}csc(\beta l)&-jZ_{o}cot(\beta l)\end{bmatrix}}{\text{ }}Z_{\text{Lossy}}={\begin{bmatrix}Z_{o}coth(\gamma l)&Z_{o}csch(\gamma l)\\Z_{o}csch(\gamma l)&Z_{o}coth(\gamma l)\end{bmatrix}}}$

Los parámetros de la matriz de dispersión (S) modelan el comportamiento eléctrico de la línea de transmisión con cargas adaptadas en cada terminación . ^[10]

Para las líneas de transmisión con y sin pérdidas respectivamente, la matriz de parámetros S es la siguiente, ^{[13] [14]} utilizando traducciones hiperbólicas estándar a complejas circulares .

${\displaystyle S_{\text{Lossless}}={\begin{bmatrix}{\frac {(Z_{o}^{2}-Z_{p}^{2})sin(\beta l)}{(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)-j2Z_{o}Z_{p}cos(\beta l)}}&{\frac {2Z_{o}Z_{p}}{j(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)+2Z_{o}Z_{p}cos(\beta l)}}\\{\frac {2Z_{o}Z_{p}}{j(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)+2Z_{o}Z_{p}cos(\beta l)}}&{\frac {(Z_{o}^{2}-Z_{p}^{2})sin(\beta l)}{(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)-j2Z_{o}Z_{p}cos(\beta l)}}\end{bmatrix}}{\text{ }}S_{\text{Lossy}}={\begin{bmatrix}{\frac {(Z_{o}^{2}-Z_{p}^{2})sinh(\gamma l)}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}&{\frac {2Z_{o}Z_{p}}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}\\{\frac {2Z_{o}Z_{p}}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}&{\frac {(Z_{o}^{2}-Z_{p}^{2})sinh(\gamma l)}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}\end{bmatrix}}}$

En todos los parámetros de matriz anteriores, se aplican las siguientes definiciones de variables:

${\displaystyle Z_{o}}$= impedancia característica

Zp = impedancia del puerto o impedancia de terminación

${\displaystyle \gamma =\alpha +j\beta }$= la constante de propagación por unidad de longitud

${\displaystyle \alpha }$= constante de atenuación en neperios por unidad de longitud

${\displaystyle \beta ={\frac {2\pi }{\lambda }}={\frac {\omega }{V}}}$= constante de número de onda o fase radianes por unidad de longitud

${\displaystyle \omega }$= frecuencia radianes / segundo

${\displaystyle V={\frac {1}{\sqrt {LC}}}={\frac {V_{C}}{\sqrt {E_{re}}}}}$= Velocidad de propagación

${\displaystyle \lambda }$= longitud de onda en unidad de longitud

L = inductancia por unidad de longitud

C = capacitancia por unidad de longitud

${\displaystyle E_{re}}$= constante dieléctrica efectiva

${\displaystyle V_{C}}$= 299.792.458 metros/segundo = Velocidad de la luz en el vacío

Las líneas de transmisión pueden colocarse cerca una de otra de tal manera que interactúen eléctricamente, como dos líneas de microbanda muy próximas. Se dice que dichas líneas de transmisión son líneas de transmisión acopladas. Las líneas de transmisión acopladas se caracterizan por un análisis de modo par e impar. El modo par se caracteriza por la excitación de los dos conductores con una señal de amplitud y fase iguales. El modo impar se caracteriza por la excitación con señales de magnitud igual y opuesta. Los modos par e impar tienen cada uno sus propias impedancias características (Zoe, Zoo) y constantes de fase ( ). Las líneas de transmisión acopladas con pérdida tienen sus propias constantes de atenuación de modo par e impar ( ), lo que a su vez conduce a constantes de propagación de modo par e impar ( ). ^{[15] [16] [17] [18] [19] [20]}${\displaystyle \beta _{e}{\text{, }}\beta _{o}}$${\displaystyle \alpha _{e}{\text{, }}\alpha _{o}}$${\displaystyle \gamma _{e}{\text{, }}\gamma _{o}}$

Las líneas de transmisión acopladas se pueden modelar utilizando parámetros de línea de transmisión de modo par e impar definidos en el párrafo anterior, como se muestra con los puertos 1 y 2 en la entrada y los puertos 3 y 4 en la salida, ^[21]

${\displaystyle {\begin{aligned}Y&={\begin{bmatrix}y11&y12&y13&y14\\y21&y22&y23&y24\\y31&y32&y33&y34\\y41&y42&y43&y44\\\end{bmatrix}}\\Z&=[Y]^{-1}\\&\\{\text{Where:}}&\\{\text{For lossless coupled lines:}}&\\y11&=y22=y33=y44={\frac {-j}{2}}{\bigg (}{\frac {cot(\beta _{e}l)}{Z_{oe}}}+{\frac {cot(\beta _{o}l)}{Z_{oo}}}{\bigg )}\\y12&=y22=y34=y43={\frac {-j}{2}}{\bigg (}{\frac {cot(\beta _{e}l)}{Z_{oe}}}-{\frac {cot(\beta _{o}l)}{Z_{oo}}}{\bigg )}\\y13&=y31=y24=y42={\frac {j}{2}}{\bigg (}{\frac {csc(\beta _{e}l)}{Z_{oe}}}+{\frac {csc(\beta _{o}l)}{Z_{oo}}}{\bigg )}\\y14&=y41=y23=y32={\frac {j}{2}}{\bigg (}{\frac {csc(\beta _{e}l)}{Z_{oe}}}-{\frac {csc(\beta _{o}l)}{Z_{oo}}}{\bigg )}\\{\text{For lossy coupled lines:}}&\\y11&=y22=y33=y44={\frac {1}{2}}{\bigg (}{\frac {coth(\gamma _{e}l)}{Z_{oe}}}+{\frac {coth(\gamma _{o}l)}{Z_{oo}}}{\bigg )}\\y12&=y22=y34=y43={\frac {1}{2}}{\bigg (}{\frac {coth(\gamma _{e}l)}{Z_{oe}}}-{\frac {coth(\gamma _{o}l)}{Z_{oo}}}{\bigg )}\\y13&=y31=y24=y42={\frac {-1}{2}}{\bigg (}{\frac {csch(\gamma _{e}l)}{Z_{oe}}}+{\frac {csch(\gamma _{o}l)}{Z_{oo}}}{\bigg )}\\y14&=y41=y23=y32={\frac {-1}{2}}{\bigg (}{\frac {csch(\gamma _{e}l)}{Z_{oe}}}-{\frac {csch(\gamma _{o}l)}{Z_{oo}}}{\bigg )}\\\end{aligned}}}$..

Las líneas coaxiales confinan prácticamente toda la onda electromagnética al área dentro del cable. Por lo tanto, las líneas coaxiales se pueden doblar y torcer (sujeto a límites) sin efectos negativos, y se pueden sujetar a soportes conductores sin inducir corrientes no deseadas en ellos. En aplicaciones de radiofrecuencia de hasta unos pocos gigahertz, la onda se propaga solo en el modo eléctrico y magnético transversal (TEM), lo que significa que los campos eléctrico y magnético son perpendiculares a la dirección de propagación (el campo eléctrico es radial y el campo magnético es circunferencial). Sin embargo, en frecuencias para las cuales la longitud de onda (en el dieléctrico) es significativamente más corta que la circunferencia del cable, se pueden propagar otros modos transversales . Estos modos se clasifican en dos grupos, modos de guía de ondas eléctricos transversales (TE) y magnéticos transversales (TM) . Cuando puede existir más de un modo, las curvas y otras irregularidades en la geometría del cable pueden hacer que la energía se transfiera de un modo a otro.

El uso más común de los cables coaxiales es para la televisión y otras señales con ancho de banda de varios megahercios. A mediados del siglo XX transportaban conexiones telefónicas de larga distancia .

Las líneas de transmisión planas son líneas de transmisión con conductores o, en algunos casos, tiras dieléctricas, que son líneas planas con forma de cinta. Se utilizan para interconectar componentes en circuitos impresos y circuitos integrados que funcionan a frecuencias de microondas porque el tipo plano se adapta bien a los métodos de fabricación de estos componentes. Existen varias formas de líneas de transmisión planas.

Un circuito de microbanda utiliza un conductor plano delgado que es paralelo a un plano de tierra . La microbanda se puede hacer colocando una tira de cobre en un lado de una placa de circuito impreso (PCB) o sustrato cerámico, mientras que el otro lado es un plano de tierra continuo. El ancho de la tira, el espesor de la capa aislante (PCB o cerámica) y la constante dieléctrica de la capa aislante determinan la impedancia característica. La microbanda es una estructura abierta, mientras que el cable coaxial es una estructura cerrada.

Un circuito de línea de transmisión utiliza una tira plana de metal que se coloca entre dos planos de tierra paralelos. El material aislante del sustrato forma un dieléctrico. El ancho de la tira, el espesor del sustrato y la permitividad relativa del sustrato determinan la impedancia característica de la tira, que es una línea de transmisión.

Una guía de ondas coplanar consta de una tira central y dos conductores exteriores adyacentes, los tres son estructuras planas que se depositan sobre el mismo sustrato aislante y, por lo tanto, se encuentran en el mismo plano ("coplanares"). El ancho del conductor central, la distancia entre los conductores interior y exterior y la permitividad relativa del sustrato determinan la impedancia característica de la línea de transmisión coplanar.

Una línea balanceada es una línea de transmisión que consta de dos conductores del mismo tipo y de igual impedancia a tierra y otros circuitos. Existen muchos formatos de líneas balanceadas, entre las más comunes se encuentran el par trenzado, el cuadrete en estrella y el bifilar.

Los pares trenzados se utilizan habitualmente para las comunicaciones telefónicas terrestres . En estos cables, se agrupan muchos pares en un solo cable, desde dos hasta varios miles. ^[22] El formato también se utiliza para la distribución de redes de datos dentro de edificios, pero el cable es más caro porque los parámetros de la línea de transmisión están estrictamente controlados.

El cable cuadrilátero en estrella es un cable de cuatro conductores en el que los cuatro conductores están trenzados juntos alrededor del eje del cable. A veces se utiliza para dos circuitos, como telefonía de 4 hilos y otras aplicaciones de telecomunicaciones. En esta configuración, cada par utiliza dos conductores no adyacentes. Otras veces se utiliza para una sola línea balanceada , como aplicaciones de audio y telefonía de 2 hilos . En esta configuración, dos conductores no adyacentes se terminan juntos en ambos extremos del cable, y los otros dos conductores también se terminan juntos.

Cuando se utiliza para dos circuitos, la diafonía se reduce en comparación con los cables con dos pares trenzados separados.

Cuando se utiliza para una única línea balanceada , la interferencia magnética captada por el cable llega como una señal de modo común prácticamente perfecta, que se elimina fácilmente mediante transformadores de acoplamiento.

Los beneficios combinados de la torsión, la señalización balanceada y el patrón cuadrupolo brindan una inmunidad al ruido excepcional, especialmente ventajosa para aplicaciones de bajo nivel de señal, como cables de micrófono, incluso cuando se instalan muy cerca de un cable de alimentación. ^{[23] [24]} La desventaja es que el cuadrupolo en estrella, al combinar dos conductores, generalmente tiene el doble de capacitancia que un cable de audio trenzado y blindado de dos conductores similar. Una alta capacitancia causa una distorsión creciente y una mayor pérdida de frecuencias altas a medida que aumenta la distancia. ^{[25] [26]}

El cable bifilar consiste en un par de conductores separados por un aislante continuo. Al mantener los conductores separados a una distancia conocida, la geometría es fija y las características de la línea son consistentes de manera confiable. Tiene menos pérdidas que el cable coaxial porque la impedancia característica del cable bifilar es generalmente más alta que la del cable coaxial, lo que genera menores pérdidas resistivas debido a la corriente reducida. Sin embargo, es más susceptible a las interferencias.

Las líneas de Lecher son una forma de conductor paralelo que se puede utilizar en UHF para crear circuitos resonantes. Son un formato práctico y conveniente que llena el espacio entre los componentes concentrados (utilizados en HF / VHF ) y las cavidades resonantes (utilizadas en UHF / SHF ).

Antiguamente, las líneas no balanceadas se utilizaban mucho para la transmisión telegráfica, pero esta forma de comunicación ha caído en desuso. Los cables son similares a los de par trenzado en el sentido de que muchos núcleos se agrupan en el mismo cable, pero solo se proporciona un conductor por circuito y no hay torsión. Todos los circuitos de la misma ruta utilizan una ruta común para la corriente de retorno (retorno a tierra). Existe una versión de transmisión de energía de retorno a tierra de un solo cable que se utiliza en muchos lugares.

Las líneas de transmisión eléctrica se utilizan ampliamente para transmitir señales de alta frecuencia a distancias cortas o largas con una pérdida mínima de potencia. Un ejemplo conocido es el cable que baja de una antena de TV o radio al receptor.

También se pueden construir una gran variedad de circuitos con líneas de transmisión, incluidos circuitos de adaptación de impedancia , filtros , divisores de potencia y acopladores direccionales .

Una línea de transmisión escalonada se utiliza para la adaptación de impedancia de amplio rango. Puede considerarse como múltiples segmentos de línea de transmisión conectados en serie, con la impedancia característica de cada elemento individual como . ^[27] La ​​impedancia de entrada se puede obtener a partir de la aplicación sucesiva de la relación de cadena${\displaystyle Z_{\mathrm {0,i} }}$

${\displaystyle Z_{\mathrm {i+1} }=Z_{\mathrm {0,i} }\,{\frac {\,Z_{\mathrm {i} }+j\,Z_{\mathrm {0,i} }\,\tan(\beta _{\mathrm {i} }\ell _{\mathrm {i} })\,}{Z_{\mathrm {0,i} }+j\,Z_{\mathrm {i} }\,\tan(\beta _{\mathrm {i} }\ell _{\mathrm {i} })}}\,}$

donde es el número de onda del -ésimo segmento de la línea de transmisión y es la longitud de este segmento, y es la impedancia del extremo frontal que carga el -ésimo segmento.${\displaystyle \beta _{\mathrm {i} }}$${\displaystyle \mathrm {i} }$${\displaystyle \ell _{\mathrm {i} }}$${\displaystyle Z_{\mathrm {i} }}$${\displaystyle \mathrm {i} }$

Debido a que la impedancia característica de cada segmento de la línea de transmisión a menudo es diferente de la impedancia del cuarto cable de entrada (que solo se muestra como una flecha marcada en el lado izquierdo del diagrama anterior), el círculo de transformación de impedancia está descentrado a lo largo del eje del diagrama de Smith, cuya representación de impedancia generalmente está normalizada contra .${\displaystyle Z_{\mathrm {0,i} }}$${\displaystyle Z_{0}}$${\displaystyle Z_{0}}$${\displaystyle x}$${\displaystyle Z_{0}}$

A frecuencias más altas, los efectos parásitos reactivos de los elementos agrupados del mundo real , incluidos los inductores y capacitores , limitan su utilidad. ^[28] Por lo tanto, a veces es útil aproximar las características eléctricas de los inductores y capacitores con líneas de transmisión a frecuencias más altas utilizando las transformaciones de Richards y luego sustituir las líneas de transmisión por los elementos agrupados. ^{[29] [30]}

Existen formas más precisas de modelado de inductores multimodo de alta frecuencia con líneas de transmisión para diseñadores avanzados. ^[31]

Si una línea de transmisión en cortocircuito o en circuito abierto se conecta en paralelo con una línea utilizada para transferir señales del punto A al punto B, funcionará como un filtro. El método para hacer los stubs es similar al método para usar líneas Lecher para la medición de frecuencias crudas, pero es "trabajar al revés". Un método recomendado en el manual de radiocomunicaciones de la RSGB es tomar un tramo de línea de transmisión en circuito abierto conectado en paralelo con el alimentador que entrega señales desde una antena. Al cortar el extremo libre de la línea de transmisión, se puede encontrar un mínimo en la intensidad de la señal observada en un receptor. En esta etapa, el filtro del stub rechazará esta frecuencia y los armónicos impares, pero si el extremo libre del stub se cortocircuita, el stub se convertirá en un filtro que rechazará los armónicos pares.

Se pueden lograr filtros de banda ancha utilizando múltiples stubs. Sin embargo, se trata de una técnica algo anticuada. Se pueden hacer filtros mucho más compactos con otros métodos, como los resonadores de líneas paralelas.

Las líneas de transmisión se utilizan como generadores de pulsos. Al cargar la línea de transmisión y luego descargarla en una carga resistiva , se puede obtener un pulso rectangular de una longitud igual al doble de la longitud eléctrica de la línea, aunque con la mitad del voltaje. Una línea de transmisión Blumlein es un dispositivo de formación de pulsos relacionado que supera esta limitación. A veces se utilizan como fuentes de energía pulsada para transmisores de radar y otros dispositivos.

La teoría de propagación de las ondas sonoras es muy similar matemáticamente a la de las ondas electromagnéticas, por lo que también se utilizan técnicas de la teoría de líneas de transmisión para construir estructuras para conducir ondas acústicas; y estas se denominan líneas de transmisión acústicas .

Wikimedia Commons tiene medios relacionados con Líneas de transmisión .

• Línea de transmisión artificial
• Onda electromagnética longitudinal
• Velocidad de propagación
• Transmisión de energía por radiofrecuencia
• Reflectómetro de dominio temporal

Parte de este artículo se deriva de la Norma Federal 1037C .

• Steinmetz, Charles Proteus (27 de agosto de 1898). "El período natural de una línea de transmisión y la frecuencia de descarga de rayos desde ella". The Electrical World : 203–205.
• Grant, IS; Phillips, WR (26 de agosto de 1991). Electromagnetismo (2.ª ed.). John Wiley. ISBN 978-0-471-92712-9.
• Ulaby, FT (2004). Fundamentos de electromagnetismo aplicado (edición de 2004). Prentice Hall. ISBN 978-0-13-185089-7.
• "Capítulo 17". Manual de comunicación por radio . Sociedad de Radio de Gran Bretaña . 1982. pág. 20. ISBN 978-0-900612-58-9.
• Naredo, JL; Soudack, AC; Marti, JR (enero de 1995). "Simulación de transitorios en líneas de transmisión con efecto corona mediante el método de características". Actas del IEE - Generación, transmisión y distribución . 142 (1): 81. doi :10.1049/ip-gtd:19951488. ISSN  1350-2360.

• Homenaje a Guglielmo Marconi. Cena anual del Instituto en el Waldorf-Astoria. Nueva York: American Institute of Electrical Engineers. 13 de enero de 1902.
• "Uso de ecuaciones y parámetros de líneas de transmisión". Manual de Star-Hspice. Software Avant!. Junio ​​de 2001. Archivado desde el original el 25 de septiembre de 2005.
• Cornille, P. (1990). "Sobre la propagación de ondas no homogéneas". Journal of Physics D: Applied Physics . 23 (2): 129–135. Bibcode :1990JPhD...23..129C. doi :10.1088/0022-3727/23/2/001. S2CID  250788839.
• Farlow, SJ (1982). Ecuaciones diferenciales parciales para científicos e ingenieros . J. Wiley and Sons. pág. 126. ISBN. 0-471-08639-8.
• Kupershmidt, Boris A. (1998). "Observaciones sobre evoluciones aleatorias en la representación hamiltoniana". J. Nonlinear Math. Phys . 5 (4): 383–395. arXiv : math-ph/9810020 . Código Bibliográfico :1998JNMP....5..483K. doi :10.2991/jnmp.1998.5.4.10. S2CID  14771417. Math-ph/9810020.
• "Adaptación de líneas de transmisión". Departamento de Ingeniería Electrónica e Informática. Diseño de circuitos de alta frecuencia. Universidad Politécnica de Hong Kong. EIE403. Archivado desde el original (PDF) el 2011-07-21 . Consultado el 2005-09-24 .
• Wilson, B. (19 de octubre de 2005). "Ecuaciones del telégrafo". Connexions. Archivado desde el original el 9 de enero de 2006.
• Wöhlbier, John Greaton (2000). Modelado y análisis de una onda viajera bajo excitación multitono (PDF) . Ingeniería eléctrica y de computación (MS). Madison, WI: Universidad de Wisconsin. §"Fundamental Equation" y §"Transforming the Telegrapher's Equations". Archivado desde el original (PDF) el 19 de junio de 2006.
• "Propagación de ondas a lo largo de una línea de transmisión" (Applet educativo de Java). Recursos educativos. Keysight Technologies.^{[ enlace muerto permanente ]} (Es posible que deba agregar "http://www.keysight.com" a su lista de sitios de excepción de Java).
• Qian, Chunqi; Brey, William W. (2009). "Adaptación de impedancia con una línea de transmisión segmentada ajustable". Journal of Magnetic Resonance . 199 (1): 104–110. Bibcode :2009JMagR.199..104Q. doi :10.1016/j.jmr.2009.04.005. PMID  19406676.

• "Calculadora de líneas de transmisión (incluidas pérdidas por radiación y excitación de ondas superficiales)". terahertz.tudelft.nl . Delft, NL: Universidad Técnica de Delft .
• "Calculadora de parámetros de líneas de transmisión". cecas.clemson.edu/cvel . Clemson, SC: Universidad de Clemson .