Matriz (estructura de datos)
Este artículo necesita citas adicionales para su verificación . ( septiembre de 2008 ) |
En informática , una matriz es una estructura de datos que consiste en una colección de elementos ( valores o variables ), del mismo tamaño de memoria, cada uno identificado por al menos un índice o clave de matriz . Una matriz se almacena de tal manera que la posición de cada elemento se puede calcular a partir de su tupla de índice mediante una fórmula matemática. [1] [2] [3] El tipo más simple de estructura de datos es una matriz lineal, también llamada matriz unidimensional.
Por ejemplo, una matriz de diez variables enteras de 32 bits (4 bytes), con índices del 0 al 9, se puede almacenar como diez palabras en las direcciones de memoria 2000, 2004, 2008, ..., 2036, (en hexadecimal : 0x7D0, 0x7D4, 0x7D8, ..., 0x7F4) de modo que el elemento con índice i tenga la dirección 2000 + ( i × 4). [4]
La dirección de memoria del primer elemento de una matriz se denomina primera dirección, dirección base o dirección de fundación.
Debido a que el concepto matemático de una matriz se puede representar como una cuadrícula bidimensional, las matrices bidimensionales también se denominan a veces "matrices". En algunos casos, el término "vector" se utiliza en informática para referirse a una matriz, aunque las tuplas en lugar de los vectores son el equivalente matemáticamente más correcto. Las tablas se implementan a menudo en forma de matrices, especialmente las tablas de búsqueda ; la palabra "tabla" a veces se utiliza como sinónimo de matriz.
Las matrices se encuentran entre las estructuras de datos más antiguas e importantes, y se utilizan en casi todos los programas. También se utilizan para implementar muchas otras estructuras de datos, como listas y cadenas . Explotan eficazmente la lógica de direccionamiento de las computadoras. En la mayoría de las computadoras modernas y en muchos dispositivos de almacenamiento externo , la memoria es una matriz unidimensional de palabras, cuyos índices son sus direcciones. Los procesadores , especialmente los procesadores vectoriales , suelen estar optimizados para operaciones con matrices.
Las matrices son útiles principalmente porque los índices de los elementos se pueden calcular en tiempo de ejecución . Entre otras cosas, esta característica permite que una única declaración iterativa procese arbitrariamente muchos elementos de una matriz. Por esa razón, se requiere que los elementos de una estructura de datos de matriz tengan el mismo tamaño y utilicen la misma representación de datos. El conjunto de tuplas de índice válidas y las direcciones de los elementos (y, por lo tanto, la fórmula de direccionamiento de elementos) suelen ser [3] [5] , pero no siempre [2], fijos mientras la matriz está en uso.
El término "matriz" también puede referirse a un tipo de datos de matriz , un tipo de datos proporcionado por la mayoría de los lenguajes de programación de alto nivel que consiste en una colección de valores o variables que pueden seleccionarse mediante uno o más índices calculados en tiempo de ejecución. Los tipos de matriz a menudo se implementan mediante estructuras de matriz; sin embargo, en algunos lenguajes pueden implementarse mediante tablas hash , listas enlazadas , árboles de búsqueda u otras estructuras de datos.
El término también se utiliza, especialmente en la descripción de algoritmos , para significar una matriz asociativa o "matriz abstracta", un modelo informático teórico (un tipo de datos abstractos o TAD) destinado a capturar las propiedades esenciales de las matrices.
Historia
Las primeras computadoras digitales usaban programación en lenguaje de máquina para configurar y acceder a estructuras de matrices para tablas de datos, cálculos de vectores y matrices y para muchos otros propósitos. John von Neumann escribió el primer programa de ordenamiento de matrices ( merge sort ) en 1945, durante la construcción de la primera computadora con programa almacenado . [6] La indexación de matrices se hacía originalmente mediante código automodificable y, más tarde, utilizando registros de índice y direccionamiento indirecto . Algunas computadoras centrales diseñadas en la década de 1960, como la Burroughs B5000 y sus sucesoras, usaban segmentación de memoria para realizar la comprobación de límites de índice en el hardware. [7]
Los lenguajes ensambladores no suelen ofrecer soporte especial para matrices, aparte del que ofrece la propia máquina. Los primeros lenguajes de programación de alto nivel, como FORTRAN (1957), Lisp (1958), COBOL (1960) y ALGOL 60 (1960), tenían soporte para matrices multidimensionales, al igual que C (1972). En C++ (1983), existen plantillas de clase para matrices multidimensionales cuya dimensión es fija en tiempo de ejecución [3] [5], así como para matrices flexibles en tiempo de ejecución. [2]
Aplicaciones
Los arreglos se utilizan para implementar vectores y matrices matemáticos , así como otros tipos de tablas rectangulares. Muchas bases de datos , pequeñas y grandes, consisten en (o incluyen) arreglos unidimensionales cuyos elementos son registros .
Las matrices se utilizan para implementar otras estructuras de datos, como listas, montones , tablas hash , deques , colas , pilas , cadenas y listas virtuales. Las implementaciones basadas en matrices de otras estructuras de datos suelen ser sencillas y eficientes en términos de espacio ( estructuras de datos implícitas ), y requieren poco espacio adicional , pero pueden tener una complejidad espacial pobre, en particular cuando se modifican, en comparación con las estructuras de datos basadas en árboles (compare una matriz ordenada con un árbol de búsqueda ).
A veces se utilizan uno o más arreglos grandes para emular la asignación de memoria dinámica dentro del programa , en particular la asignación de grupos de memoria . Históricamente, esta ha sido a veces la única forma de asignar "memoria dinámica" de forma portable.
Las matrices se pueden utilizar para determinar el flujo de control parcial o completo en los programas, como una alternativa compacta a IFlas instrucciones múltiples (que de otro modo serían repetitivas). En este contexto, se las conoce como tablas de control y se utilizan junto con un intérprete diseñado específicamente cuyo flujo de control se modifica según los valores contenidos en la matriz. La matriz puede contener punteros de subrutina (o números de subrutina relativos sobre los que se puede actuar mediante instrucciones SWITCH ) que dirigen la ruta de la ejecución.
Identificador de elementos y fórmulas de direccionamiento
Cuando los objetos de datos se almacenan en una matriz, los objetos individuales se seleccionan mediante un índice que suele ser un entero escalar no negativo . Los índices también se denominan subíndices. Un índice asigna el valor de la matriz a un objeto almacenado.
Hay tres formas en las que se pueden indexar los elementos de una matriz:
- 0 ( indexación basada en cero )
- El primer elemento de la matriz está indexado por el subíndice 0. [8]
- 1 ( indexación basada en uno )
- El primer elemento de la matriz está indexado por el subíndice 1.
- n ( indexación basada en n )
- El índice base de una matriz se puede elegir libremente. Por lo general, los lenguajes de programación que permiten la indexación basada en n también permiten valores de índice negativos y otros tipos de datos escalares , como enumeraciones o caracteres , se pueden usar como índice de matriz.
El uso de indexación basada en cero es la opción de diseño de muchos lenguajes de programación influyentes, incluidos C , Java y Lisp . Esto conduce a una implementación más simple donde el subíndice hace referencia a un desplazamiento desde la posición inicial de una matriz, por lo que el primer elemento tiene un desplazamiento de cero.
Las matrices pueden tener múltiples dimensiones, por lo que no es raro acceder a una matriz mediante múltiples índices. Por ejemplo, una matriz bidimensional Acon tres filas y cuatro columnas podría proporcionar acceso al elemento en la segunda fila y la cuarta columna mediante la expresión A[1][3]en el caso de un sistema de indexación basado en cero. Por lo tanto, se utilizan dos índices para una matriz bidimensional, tres para una matriz tridimensional y n para una matriz n -dimensional.
La cantidad de índices necesarios para especificar un elemento se denomina dimensión, dimensionalidad o rango de la matriz.
En las matrices estándar, cada índice está restringido a un cierto rango de números enteros consecutivos (o valores consecutivos de algún tipo enumerado ), y la dirección de un elemento se calcula mediante una fórmula "lineal" en los índices.
Matrices unidimensionales

Una matriz unidimensional (o matriz de una sola dimensión) es un tipo de matriz lineal. Para acceder a sus elementos se necesita un único subíndice que puede representar un índice de fila o de columna.
Como ejemplo, considere la declaración de C int anArrayName[10];que declara una matriz unidimensional de diez números enteros. Aquí, la matriz puede almacenar diez elementos de tipo int. Esta matriz tiene índices que comienzan desde cero hasta nueve. Por ejemplo, las expresiones anArrayName[0]y anArrayName[9]son el primer y el último elemento respectivamente.
Para un vector con direccionamiento lineal, el elemento con índice i se ubica en la dirección B + c · i , donde B es una dirección base fija y c una constante fija, a veces llamada incremento o paso de dirección .
Si los índices de elementos válidos comienzan en 0, la constante B es simplemente la dirección del primer elemento de la matriz. Por este motivo, el lenguaje de programación C especifica que los índices de las matrices siempre comienzan en 0; y muchos programadores llamarán a ese elemento " cero " en lugar de "primero".
Sin embargo, se puede elegir el índice del primer elemento mediante una elección adecuada de la dirección base B. Por ejemplo, si la matriz tiene cinco elementos, indexados del 1 al 5, y la dirección base B se reemplaza por B + 30 c , entonces los índices de esos mismos elementos serán del 31 al 35. Si la numeración no comienza en 0, la constante B puede no ser la dirección de ningún elemento.

Matrices multidimensionales

Para una matriz multidimensional, el elemento con índices i , j tendría la dirección B + c · i + d · j , donde los coeficientes c y d son los incrementos de las direcciones de fila y columna , respectivamente.
De manera más general, en una matriz k -dimensional, la dirección de un elemento con índices i 1 , i 2 , ..., i k es
- B + c 1 · i 1 + c 2 · i 2 + … + c k · i k .
Por ejemplo: int a[2][3];
Esto significa que la matriz a tiene 2 filas y 3 columnas, y la matriz es de tipo entero. Aquí podemos almacenar 6 elementos que se almacenarán de forma lineal, pero comenzando por la primera fila de forma lineal y luego continuando con la segunda fila. La matriz anterior se almacenará como a 11 , a 12 , a 13 , a 21 , a 22 , a 23 .
Esta fórmula requiere solo k multiplicaciones y k sumas para cualquier matriz que quepa en la memoria. Además, si algún coeficiente es una potencia fija de 2, la multiplicación se puede reemplazar por desplazamiento de bits .
Los coeficientes c k deben elegirse de manera que cada tupla de índice válida se asigne a la dirección de un elemento distinto.
Si el valor mínimo legal para cada índice es 0, entonces B es la dirección del elemento cuyos índices son todos cero. Como en el caso unidimensional, los índices de los elementos pueden cambiarse modificando la dirección base B. Por lo tanto, si una matriz bidimensional tiene filas y columnas indexadas de 1 a 10 y de 1 a 20, respectivamente, entonces reemplazar B por B + c 1 − 3 c 2 hará que se vuelvan a numerar de 0 a 9 y de 4 a 23, respectivamente. Aprovechando esta característica, algunos lenguajes (como FORTRAN 77) especifican que los índices de las matrices comiencen en 1, como en la tradición matemática, mientras que otros lenguajes (como Fortran 90, Pascal y Algol) permiten al usuario elegir el valor mínimo para cada índice.
Vectores de droga
La fórmula de direccionamiento está completamente definida por la dimensión d , la dirección base B y los incrementos c 1 , c 2 , ..., c k . A menudo es útil empaquetar estos parámetros en un registro llamado descriptor de la matriz, vector de paso o vector dope . [2] [3] El tamaño de cada elemento y los valores mínimos y máximos permitidos para cada índice también pueden incluirse en el vector dope. El vector dope es un controlador completo para la matriz y es una forma conveniente de pasar matrices como argumentos a procedimientos . Muchas operaciones útiles de segmentación de matrices (como seleccionar una submatriz, intercambiar índices o invertir la dirección de los índices) se pueden realizar de manera muy eficiente manipulando el vector dope. [2]
Diseños compactos
A menudo, los coeficientes se eligen de modo que los elementos ocupen un área contigua de la memoria. Sin embargo, esto no es necesario. Incluso si las matrices se crean siempre con elementos contiguos, algunas operaciones de segmentación de matrices pueden crear submatrices no contiguas a partir de ellas.

Existen dos diseños sistemáticos compactos para una matriz bidimensional. Por ejemplo, considere la matriz
En el diseño de orden de fila principal (adoptado por C para matrices declaradas estáticamente), los elementos de cada fila se almacenan en posiciones consecutivas y todos los elementos de una fila tienen una dirección menor que cualquiera de los elementos de una fila consecutiva:
1 2 3 4 5 6 7 8 9
En el orden de columna principal (tradicionalmente utilizado por Fortran), los elementos de cada columna son consecutivos en la memoria y todos los elementos de una columna tienen una dirección menor que cualquiera de los elementos de una columna consecutiva:
1 4 7 2 5 8 3 6 9
En el caso de matrices con tres o más índices, el "orden principal de fila" coloca en posiciones consecutivas dos elementos cualesquiera cuyas tuplas de índices difieren solo en uno en el último índice. El "orden principal de columna" es análogo con respecto al primer índice.
En sistemas que utilizan la memoria caché del procesador o la memoria virtual , el escaneo de una matriz es mucho más rápido si los elementos sucesivos se almacenan en posiciones consecutivas en la memoria, en lugar de estar dispersos de forma dispersa. Esto se conoce como localidad espacial, que es un tipo de localidad de referencia . Muchos algoritmos que utilizan matrices multidimensionales las escanearán en un orden predecible. Un programador (o un compilador sofisticado) puede utilizar esta información para elegir entre un diseño por filas o por columnas para cada matriz. Por ejemplo, al calcular el producto A · B de dos matrices, sería mejor tener A almacenada en orden por filas y B en orden por columnas.
Cambio de tamaño
Las matrices estáticas tienen un tamaño fijo cuando se crean y, en consecuencia, no permiten insertar ni eliminar elementos. Sin embargo, al asignar una nueva matriz y copiar el contenido de la matriz anterior en ella, es posible implementar de manera efectiva una versión dinámica de una matriz; consulte matriz dinámica . Si esta operación se realiza con poca frecuencia, las inserciones al final de la matriz solo requieren tiempo constante amortizado.
Algunas estructuras de datos de matriz no reasignan el almacenamiento, pero sí almacenan un recuento de la cantidad de elementos de la matriz en uso, denominado recuento o tamaño. Esto convierte a la matriz en una matriz dinámica con un tamaño o capacidad máximos fijos; las cadenas de Pascal son ejemplos de esto.
Fórmulas no lineales
En ocasiones se utilizan fórmulas más complicadas (no lineales). Por ejemplo, para una matriz triangular bidimensional compacta , la fórmula de direccionamiento es un polinomio de grado 2.
Eficiencia
Tanto el almacenamiento como la selección toman un tiempo constante (en el peor de los casos, determinista) . Las matrices ocupan un espacio lineal ( O ( n )) en la cantidad de elementos n que contienen.
En una matriz con un tamaño de elemento k y en una máquina con un tamaño de línea de caché de B bytes, iterar a través de una matriz de n elementos requiere el mínimo de errores de caché de ceiling( nk /B), porque sus elementos ocupan ubicaciones de memoria contiguas. Esto es aproximadamente un factor de B/ k mejor que el número de errores de caché necesarios para acceder a n elementos en ubicaciones de memoria aleatorias. Como consecuencia, la iteración secuencial sobre una matriz es notablemente más rápida en la práctica que la iteración sobre muchas otras estructuras de datos, una propiedad llamada localidad de referencia (esto no significa, sin embargo, que usar un hash perfecto o un hash trivial dentro de la misma matriz (local), no sea aún más rápido -y alcanzable en tiempo constante ). Las bibliotecas proporcionan facilidades optimizadas de bajo nivel para copiar rangos de memoria (como memcpy ) que se pueden usar para mover bloques contiguos de elementos de matriz significativamente más rápido de lo que se puede lograr a través del acceso a elementos individuales. La aceleración de tales rutinas optimizadas varía según el tamaño del elemento de la matriz, la arquitectura y la implementación.
En términos de memoria, las matrices son estructuras de datos compactas sin sobrecarga por elemento . Puede haber una sobrecarga por matriz (por ejemplo, para almacenar límites de índice), pero esto depende del lenguaje. También puede suceder que los elementos almacenados en una matriz requieran menos memoria que los mismos elementos almacenados en variables individuales, porque varios elementos de la matriz se pueden almacenar en una sola palabra ; a estas matrices se las suele llamar matrices empaquetadas . Un caso extremo (pero de uso común) es la matriz de bits , donde cada bit representa un solo elemento. Un solo octeto puede contener hasta 256 combinaciones diferentes de hasta 8 condiciones diferentes, en la forma más compacta.
Los accesos a matrices con patrones de acceso estáticamente predecibles son una fuente importante de paralelismo de datos .
Comparación con otras estructuras de datos
| Vistazo (índice) | Mutar (insertar o eliminar) en… | Exceso de espacio, promedio | |||
|---|---|---|---|---|---|
| Comienzo | Fin | Medio | |||
| Lista enlazada | Θ( n ) | Θ(1) | Θ(1), elemento final conocido; Θ( n ), elemento final desconocido | Θ( n ) | Θ( n ) |
| Formación | Θ(1) | — | — | — | 0 |
| Matriz dinámica | Θ(1) | Θ( n ) | Θ(1) amortizado | Θ( n ) | Θ( n ) [9] |
| Árbol equilibrado | Θ(log n) | Θ(log n) | Θ(log n ) | Θ(log n ) | Θ( n ) |
| Lista de acceso aleatorio | Θ(log n) [10] | Θ(1) | — [10] | — [10] | Θ( n ) |
| Árbol de matriz hash | Θ(1) | Θ( n ) | Θ(1) amortizado | Θ( n ) | Θ(√ n ) |
Las matrices dinámicas o ampliables son similares a las matrices, pero añaden la capacidad de insertar y eliminar elementos; la adición y eliminación al final es particularmente eficiente. Sin embargo, reservan almacenamiento adicional lineal ( Θ ( n )), mientras que las matrices no reservan almacenamiento adicional.
Las matrices asociativas proporcionan un mecanismo para una funcionalidad similar a la de las matrices sin grandes sobrecargas de almacenamiento cuando los valores de índice son escasos. Por ejemplo, una matriz que contiene valores solo en los índices 1 y 2 mil millones puede beneficiarse del uso de dicha estructura. Las matrices asociativas especializadas con claves enteras incluyen los intentos Patricia , las matrices Judy y los árboles de van Emde Boas .
Los árboles equilibrados requieren un tiempo O(log n ) para el acceso indexado, pero también permiten insertar o eliminar elementos en un tiempo O(log n ), [11] mientras que las matrices ampliables requieren un tiempo lineal (Θ( n )) para insertar o eliminar elementos en una posición arbitraria.
Las listas enlazadas permiten la eliminación e inserción en tiempo constante en el medio, pero requieren un tiempo lineal para el acceso indexado. Su uso de memoria suele ser peor que el de las matrices, pero sigue siendo lineal.
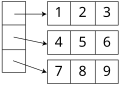
Un vector de Iliffe es una alternativa a una estructura de matriz multidimensional. Utiliza una matriz unidimensional de referencias a matrices de una dimensión menos. Para dos dimensiones, en particular, esta estructura alternativa sería un vector de punteros a vectores, uno para cada fila (puntero en c o c++). Por lo tanto, se accedería a un elemento en la fila i y la columna j de una matriz A mediante una doble indexación ( A [ i ][ j ] en la notación típica). Esta estructura alternativa permite matrices escalonadas , donde cada fila puede tener un tamaño diferente o, en general, donde el rango válido de cada índice depende de los valores de todos los índices anteriores. También ahorra una multiplicación (por el incremento de la dirección de la columna) reemplazándola por un desplazamiento de bit (para indexar el vector de punteros de fila) y un acceso de memoria adicional (obteniendo la dirección de fila), lo que puede valer la pena en algunas arquitecturas.
Dimensión
La dimensión de una matriz es el número de índices necesarios para seleccionar un elemento. Por lo tanto, si la matriz se considera como una función de un conjunto de posibles combinaciones de índices, es la dimensión del espacio cuyo dominio es un subconjunto discreto. Por lo tanto, una matriz unidimensional es una lista de datos, una matriz bidimensional es un rectángulo de datos, [12] una matriz tridimensional es un bloque de datos, etc.
Esto no debe confundirse con la dimensión del conjunto de todas las matrices con un dominio dado, es decir, el número de elementos de la matriz. Por ejemplo, una matriz con 5 filas y 4 columnas es bidimensional, pero tales matrices forman un espacio de 20 dimensiones. De manera similar, un vector tridimensional puede representarse mediante una matriz unidimensional de tamaño tres.
Véase también
Referencias
- ^ Black, Paul E. (13 de noviembre de 2008). "array". Diccionario de algoritmos y estructuras de datos . Instituto Nacional de Estándares y Tecnología . Consultado el 22 de agosto de 2010 .
- ^ abcde Bjoern Andres; Ullrich Koethe; Thorben Kroeger; Hamprecht (2010). "Matrices y vistas multidimensionales flexibles en tiempo de ejecución para C++98 y C++0x". arXiv : 1008.2909 [cs.DS].
- ^ abcd Garcia, Ronald; Lumsdaine, Andrew (2005). "MultiArray: una biblioteca C++ para programación genérica con arreglos". Software: Práctica y Experiencia . 35 (2): 159–188. doi :10.1002/spe.630. ISSN 0038-0644. S2CID 10890293.
- ^ David R. Richardson (2002), El libro sobre estructuras de datos. iUniverse, 112 páginas. ISBN 0-595-24039-9 , ISBN 978-0-595-24039-5 .
- ^ ab Veldhuizen, Todd L. (diciembre de 1998). Arrays in Blitz++ . Computing in Object-Oriented Parallel Environments. Lecture Notes in Computer Science. Vol. 1505. Berlín: Springer. págs. 223–230. doi :10.1007/3-540-49372-7_24. ISBN 978-3-540-65387-5.[ enlace muerto ]
- ^ Knuth, Donald (1998). Ordenación y búsqueda . El arte de la programación informática . Vol. 3. Reading, MA: Addison-Wesley Professional. pág. 159.
- ^ Levy, Henry M. (1984), Sistemas informáticos basados en capacidades , Digital Press, pág. 22, ISBN 9780932376220.
- ^ "Ejemplos de código de matriz - Funciones de matriz PHP - Código PHP". Consejos de programación web. Archivado desde el original el 13 de abril de 2011. Consultado el 8 de abril de 2011. En la mayoría de los lenguajes informáticos ,
el índice de la matriz (conteo) comienza desde 0, no desde 1. El índice del primer elemento de la matriz es 0, el índice del segundo elemento de la matriz es 1, y así sucesivamente. En la matriz de nombres a continuación, puede ver índices y valores.
- ^ Brodnik, Andrej; Carlsson, Svante; Sedgewick, Robert ; Munro, JI; Demaine, ED (1999), Matrices redimensionables en tiempo y espacio óptimos (Informe técnico CS-99-09) (PDF) , Departamento de Ciencias de la Computación, Universidad de Waterloo
- ^ abc Chris Okasaki (1995). "Listas de acceso aleatorio puramente funcionales". Actas de la Séptima Conferencia Internacional sobre Lenguajes de Programación Funcional y Arquitectura de Computadoras : 86–95. doi :10.1145/224164.224187.
- ^ "Árboles B contados".
- ^ "Matrices bidimensionales \ Processing.org". processing.org . Consultado el 1 de mayo de 2020 .




