Línea de campo

Una línea de campo es una ayuda visual gráfica para visualizar campos vectoriales . Consiste en una curva integral imaginaria que es tangente al vector de campo en cada punto a lo largo de su longitud. ^{[1] [2]} Un diagrama que muestra un conjunto representativo de líneas de campo vecinas es una forma común de representar un campo vectorial en la literatura científica y matemática; esto se llama diagrama de línea de campo . Se utilizan para mostrar campos eléctricos , campos magnéticos y campos gravitacionales entre muchos otros tipos. En mecánica de fluidos , las líneas de campo que muestran el campo de velocidad de un flujo de fluido se denominan líneas de corriente .

Un campo vectorial define una dirección y una magnitud en cada punto del espacio. Una línea de campo es una curva integral para ese campo vectorial y puede construirse comenzando en un punto y trazando una línea a través del espacio que siga la dirección del campo vectorial, haciendo que la línea de campo sea tangente al vector de campo en cada punto. ^{[3] [2] [1]} Una línea de campo se muestra generalmente como un segmento de línea dirigido, con una punta de flecha que indica la dirección del campo vectorial. Para campos bidimensionales, las líneas de campo son curvas planas; dado que un dibujo plano de un conjunto tridimensional de líneas de campo puede ser visualmente confuso, la mayoría de los diagramas de líneas de campo son de este tipo. Dado que en cada punto donde es distinto de cero y finito el campo vectorial tiene una dirección única, las líneas de campo nunca pueden intersecarse, por lo que hay exactamente una línea de campo que pasa por cada punto en el que el campo vectorial es distinto de cero y finito. ^{[3] [2]} Los puntos donde el campo es cero o infinito no tienen una línea de campo que los atraviese, ya que la dirección no se puede definir allí, pero pueden ser los puntos finales de las líneas de campo.

Como en cualquier región hay un número infinito de puntos, se puede dibujar un número infinito de líneas de campo, pero sólo se puede mostrar un número limitado de ellas en un diagrama de líneas de campo. Por lo tanto, la elección de las líneas de campo que se muestran depende de la persona o del programa informático que dibuja el diagrama, y ​​un único campo vectorial puede representarse mediante diferentes conjuntos de líneas de campo. Un diagrama de líneas de campo es necesariamente una descripción incompleta de un campo vectorial, ya que no proporciona información sobre el campo entre las líneas de campo dibujadas, y la elección de cuántas y cuáles líneas mostrar determina la cantidad de información útil que proporciona el diagrama.

Una línea de campo individual muestra la dirección del campo vectorial, pero no su magnitud . Para representar también la magnitud del campo, los diagramas de líneas de campo suelen dibujarse de modo que cada línea represente la misma cantidad de flujo . Entonces, la densidad de líneas de campo (número de líneas de campo por unidad de área perpendicular) en cualquier ubicación es proporcional a la magnitud del campo vectorial en ese punto. Las áreas en las que las líneas de campo vecinas convergen (se acercan) indican que el campo se está haciendo más intenso en esa dirección.

En los campos vectoriales que tienen divergencia distinta de cero , las líneas de campo comienzan en puntos de divergencia positiva ( fuentes ) y terminan en puntos de divergencia negativa ( sumideros ), o se extienden hasta el infinito. Por ejemplo, las líneas de campo eléctrico comienzan en cargas eléctricas positivas y terminan en cargas negativas. En campos sin divergencia ( solenoideos ), como los campos magnéticos , las líneas de campo no tienen puntos finales; son bucles cerrados o son infinitas. ^{[4] [5]}

En física, los dibujos de líneas de campo son principalmente útiles en casos en los que las fuentes y los sumideros, si los hay, tienen un significado físico, a diferencia de, por ejemplo, el caso de un campo de fuerza de un armónico radial . Por ejemplo, la ley de Gauss establece que un campo eléctrico tiene fuentes en cargas positivas , sumideros en cargas negativas y ninguno en otro lugar, por lo que las líneas de campo eléctrico comienzan en cargas positivas y terminan en cargas negativas. Un campo gravitacional no tiene fuentes, tiene sumideros en masas y no tiene ninguno en otro lugar, las líneas de campo gravitacional vienen del infinito y terminan en masas. Un campo magnético no tiene fuentes ni sumideros ( ley de Gauss para el magnetismo ), por lo que sus líneas de campo no tienen inicio ni fin: solo pueden formar bucles cerrados, extenderse hasta el infinito en ambas direcciones o continuar indefinidamente sin cruzarse nunca. Sin embargo, como se dijo anteriormente, puede ocurrir una situación especial alrededor de los puntos donde el campo es cero (que no pueden ser intersectados por líneas de campo, porque su dirección no estaría definida) y tiene lugar el inicio y el final simultáneos de las líneas de campo. Esta situación se da, por ejemplo, en el punto intermedio entre dos cargas eléctricas puntuales positivas idénticas. Allí, el campo desaparece y las líneas que salen axialmente de las cargas terminan. Al mismo tiempo, en el plano transversal que pasa por el punto intermedio, un número infinito de líneas de campo divergen radialmente. La presencia concomitante de las líneas que terminan y comienzan preserva el carácter libre de divergencia del campo en el punto. ^[5]

Tenga en cuenta que para este tipo de dibujo, donde se pretende que la densidad de líneas de campo sea proporcional a la magnitud del campo, es importante representar las tres dimensiones. Por ejemplo, considere el campo eléctrico que surge de una única carga puntual aislada . Las líneas de campo eléctrico en este caso son líneas rectas que emanan de la carga de manera uniforme en todas las direcciones en el espacio tridimensional. Esto significa que su densidad es proporcional a , el resultado correcto consistente con la ley de Coulomb para este caso. Sin embargo, si las líneas de campo eléctrico para esta configuración se dibujaran simplemente en un plano bidimensional, su densidad bidimensional sería proporcional a , un resultado incorrecto para esta situación. ^[6]$Estilo de visualización 1/r^{2}}$${\estilo de visualización 1/r}$

Dado un campo vectorial y un punto de partida, se puede construir una línea de campo de forma iterativa hallando el vector de campo en ese punto . El vector tangente unitario en ese punto es: . Moviéndose una distancia corta a lo largo de la dirección del campo se puede hallar un nuevo punto en la línea. Luego se halla el campo en ese punto y moviéndose una distancia más en esa dirección se halla el siguiente punto de la línea de campo. En cada punto se puede hallar el siguiente punto mediante Al repetir esto y conectar los puntos, la línea de campo se puede extender tanto como se desee. Esto es solo una aproximación a la línea de campo real, ya que cada segmento recto no es realmente tangente al campo a lo largo de su longitud, solo en su punto de partida. Pero al usar un valor lo suficientemente pequeño para , dando un mayor número de pasos más cortos, la línea de campo se puede aproximar tanto como se desee. La línea de campo se puede extender en la dirección opuesta de dando cada paso en la dirección opuesta mediante un paso negativo .${\displaystyle \mathbf {F} (\mathbf {x} )}$${\displaystyle \mathbf {x} _ {\text{0}}}$${\displaystyle \mathbf {F} (\mathbf {x} _ {\text{0}})}$${\displaystyle \mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|}$${\estilo de visualización ds}$$${\displaystyle \mathbf {x} _{\text{1}}=\mathbf {x} _{\text{0}}+{\mathbf {F} (\mathbf {x} _{\text{0}}) \sobre |\mathbf {F} (\mathbf {x} _{\text{0}})|}ds}$$${\displaystyle \mathbf {F} (\mathbf {x} _{\text{1}})}$${\estilo de visualización ds}$${\displaystyle \mathbf {F} (\mathbf {x} _{\text{2}})}$${\displaystyle \mathbf {x} _{\text{i}}}$$${\displaystyle \mathbf {x} _{\text{i+1}}=\mathbf {x} _{\text{i}}+{\mathbf {F} (\mathbf {x} _{\text{i}}) \sobre |\mathbf {F} (\mathbf {x} _{\text{i}})|}ds}$$${\estilo de visualización ds}$${\displaystyle \mathbf {x} _ {\text{0}}}$${\estilo de visualización -ds}$

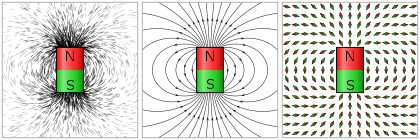
Si el campo vectorial describe un campo de velocidad , entonces las líneas de campo siguen las líneas de corriente en el flujo. Quizás el ejemplo más conocido de un campo vectorial descrito por líneas de campo es el campo magnético , que a menudo se representa utilizando líneas de campo que emanan de un imán .

Las líneas de campo se pueden utilizar para rastrear cantidades familiares del cálculo vectorial :

• La divergencia se puede ver fácilmente a través de las líneas de campo, suponiendo que las líneas se dibujan de manera que la densidad de las líneas de campo sea proporcional a la magnitud del campo (ver arriba). En este caso, la divergencia se puede ver como el comienzo y el final de las líneas de campo. Si el campo vectorial es el resultado de campos de ley radial del inverso del cuadrado con respecto a una o más fuentes, esto corresponde al hecho de que la divergencia de dicho campo es cero fuera de las fuentes. En un campo vectorial solenoidal (es decir, un campo vectorial donde la divergencia es cero en todas partes), las líneas de campo no comienzan ni terminan; forman bucles cerrados o se extienden hasta el infinito en ambas direcciones. Si un campo vectorial tiene divergencia positiva en algún área, habrá líneas de campo que comiencen en puntos de esa área. Si un campo vectorial tiene divergencia negativa en algún área, habrá líneas de campo que terminen en puntos de esa área.
• El teorema de Kelvin-Stokes muestra que las líneas de campo de un campo vectorial con rotacional cero (es decir, un campo vectorial conservativo , por ejemplo, un campo gravitacional o un campo electrostático ) no pueden ser bucles cerrados. En otras palabras, el rotacional siempre está presente cuando una línea de campo forma un bucle cerrado. También puede estar presente en otras situaciones, como una forma helicoidal de líneas de campo.

Si bien las líneas de campo son una "mera" construcción matemática, en algunas circunstancias adquieren importancia física. En mecánica de fluidos , las líneas de campo de velocidad ( líneas de corriente ) en flujo constante representan las trayectorias de las partículas del fluido. En el contexto de la física del plasma , los electrones o iones que se encuentran en la misma línea de campo interactúan fuertemente, mientras que las partículas en diferentes líneas de campo en general no interactúan. Este es el mismo comportamiento que exhiben las partículas de limaduras de hierro en un campo magnético.

Las limaduras de hierro de la fotografía parecen alinearse con líneas de campo discretas, pero la situación es más compleja. Es fácil visualizarla como un proceso de dos etapas: primero, las limaduras se distribuyen uniformemente sobre el campo magnético, pero todas están alineadas en la dirección del campo. Luego, en función de la escala y las propiedades ferromagnéticas de las limaduras, amortiguan el campo hacia ambos lados, creando los espacios aparentes entre las líneas que vemos. ^{[ cita requerida ]} Por supuesto, las dos etapas descritas aquí ocurren simultáneamente hasta que se alcanza un equilibrio. Debido a que el magnetismo intrínseco de las limaduras modifica el campo, las líneas que muestran las limaduras son solo una aproximación de las líneas de campo del campo magnético original. Los campos magnéticos son continuos y no tienen líneas discretas.

• Campo de fuerza (física)
• Líneas de campo de los conjuntos de Julia
• Rayos externos : líneas de campo del potencial de Douady-Hubbard del conjunto de Mandelbrot o conjuntos de Julia rellenados
• Línea de fuerza
• Campo vectorial
• Convolución integral de línea

Wikimedia Commons tiene medios relacionados con Diagramas de campo .

• Aplicación interactiva de Java que muestra las líneas de campo eléctrico de pares de cargas seleccionados Archivado el 13 de agosto de 2011 en Wayback Machine por Wolfgang Bauer
• "Visualización de campos, divergencia y rizo", notas del curso en el Instituto Tecnológico de Massachusetts.