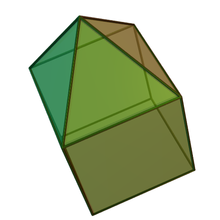
Pirámide cuadrada alargada

Pirámide cuadrada alargada
Tipo	Johnson J 7 – J 8 – J 9
Caras	4 triángulos 1+4 cuadrados
Bordes	16
Vértices	9
Configuración de vértice	${\displaystyle 4\veces (4^{3})}$ ${\displaystyle 1\veces (3^{4})}$ ${\displaystyle 4\veces (3^{2}\veces 4^{2})}$
Grupo de simetría	$Estilo de visualización C_{4v}$
Angulo diedro ( grados )	De triángulo a triángulo: 109,47° De cuadrado a cuadrado: 90° Triángulo a cuadrado: 144,74°
Propiedades	convexo , compuesto
Neto

En geometría , la pirámide cuadrada alargada es un poliedro convexo construido a partir de un cubo uniendo una pirámide cuadrada equilátera a una de sus caras. Es un ejemplo de sólido de Johnson .

La bipirámide cuadrada alargada es un compuesto , ya que se puede construir uniendo dos pirámides cuadradas equiláteras a las caras de un cubo que están opuestas entre sí, un proceso conocido como elongación . ^{[1] [2]} Esta construcción implica la eliminación de esos dos cuadrados y su reemplazo por esas pirámides, lo que da como resultado ocho triángulos equiláteros y cuatro cuadrados como sus caras. ^[3] Un poliedro convexo en el que todas sus caras son regulares es un sólido de Johnson , y la bipirámide cuadrada alargada es uno de ellos, denotado como , el decimoquinto sólido de Johnson. ^[4]$Estilo de visualización J_{15}}$

Dado que es la longitud del borde de una pirámide cuadrada alargada. La altura de una pirámide cuadrada alargada se puede calcular sumando la altura de una pirámide cuadrada equilátera y un cubo. La altura de un cubo es la misma que la longitud del borde del lado de un cubo, y la altura de una pirámide cuadrada equilátera es . Por lo tanto, la altura de una bipirámide cuadrada alargada es: ^[5] Su área de superficie se puede calcular sumando todas las áreas de cuatro triángulos equiláteros y cuatro cuadrados: ^[3] Su volumen se obtiene dividiendo la pirámide en una pirámide cuadrada equilátera y un cubo, y luego sumándolos: ^[3]${\estilo de visualización a}$${\displaystyle (1/{\sqrt {2}})a}$$${\displaystyle a+{\frac {1}{\sqrt {2}}}a=\left(1+{\frac {\sqrt {2}}{2}}\right)a\approx 1.707a.}$$$${\displaystyle \left(5+{\sqrt {3}}\right)a^{2}\aproximadamente 6,732a^{2}.}$$$${\displaystyle \left(1+{\frac {\sqrt {2}}{6}}\right)a^{3}\aproximadamente 1,236a^{3}.}$$

La pirámide cuadrada alargada tiene el mismo grupo de simetría tridimensional que la pirámide cuadrada equilátera, el grupo cíclico de orden ocho. Su ángulo diedro se puede obtener sumando el ángulo de una pirámide cuadrada equilátera y un cubo: ^[6]$Estilo de visualización C_{4v}$

• El ángulo diedro de una bipirámide cuadrada alargada entre dos triángulos adyacentes es el ángulo diedro de un triángulo equilátero entre sus caras laterales ,${\displaystyle \arccos(-1/3)\aproximadamente 109,47^{\circ }}$
• El ángulo diedro de una bipirámide cuadrada alargada entre dos cuadrados adyacentes es el ángulo diedro de un cubo entre aquellos ,${\displaystyle \pi /2=90^{\circ }}$
• El ángulo diedro de una pirámide cuadrada equilátera entre un cuadrado y un triángulo es . Por lo tanto, el ángulo diedro de una bipirámide cuadrada alargada entre un triángulo y un cuadrado, en el borde donde las pirámides cuadradas equiláteras se unen al cubo, es${\displaystyle \arctan \left({\sqrt {2}}\right)\aproximadamente 54,74^{\circ }}$$${\displaystyle \arctan \left({\sqrt {2}}\right)+{\frac {\pi }{2}}\approx 144.74^{\circ }.}$$

• Bipirámide cuadrada alargada

• Weisstein, Eric W. , "Sólido de Johnson" ("Pirámide cuadrada alargada") en MathWorld .