Muestreo (procesamiento de señales)
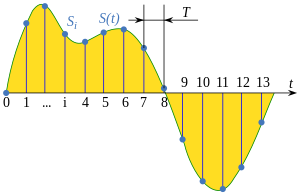
En el procesamiento de señales , el muestreo es la reducción de una señal de tiempo continuo a una señal de tiempo discreto . Un ejemplo común es la conversión de una onda de sonido en una secuencia de "muestras". Una muestra es un valor de la señal en un punto en el tiempo y/o el espacio; esta definición difiere del uso del término en estadística , que se refiere a un conjunto de dichos valores. [A]
Un muestreador es un subsistema u operación que extrae muestras de una señal continua . Un muestreador ideal teórico produce muestras equivalentes al valor instantáneo de la señal continua en los puntos deseados.
La señal original se puede reconstruir a partir de una secuencia de muestras, hasta el límite de Nyquist , pasando la secuencia de muestras a través de un filtro de reconstrucción .
Teoría
Se pueden muestrear funciones de espacio, tiempo o cualquier otra dimensión, y lo mismo ocurre en dos o más dimensiones.
Para funciones que varían con el tiempo, sea una función continua (o "señal") a muestrear, y sea que el muestreo se realice midiendo el valor de la función continua cada segundos, lo que se denomina intervalo de muestreo o período de muestreo . [1] [2] Entonces la función muestreada está dada por la secuencia:
- , para valores enteros de .
La frecuencia de muestreo o tasa de muestreo , , es el número promedio de muestras obtenidas en un segundo, por lo tanto , con la unidad muestras por segundo , a veces denominada hercio , por ejemplo 48 kHz son 48.000 muestras por segundo .
La reconstrucción de una función continua a partir de muestras se realiza mediante algoritmos de interpolación. La fórmula de interpolación de Whittaker-Shannon es matemáticamente equivalente a un filtro de paso bajo ideal cuya entrada es una secuencia de funciones delta de Dirac que se modulan (multiplican) por los valores de la muestra. Cuando el intervalo de tiempo entre muestras adyacentes es una constante , la secuencia de funciones delta se denomina peine de Dirac . Matemáticamente, el peine de Dirac modulado es equivalente al producto de la función peine por . Esa abstracción matemática a veces se denomina muestreo por impulsos . [3]
La mayoría de las señales muestreadas no se almacenan y reconstruyen simplemente. La fidelidad de una reconstrucción teórica es una medida común de la eficacia del muestreo. Esa fidelidad se reduce cuando contiene componentes de frecuencia cuya longitud de ciclo (periodo) es inferior a 2 intervalos de muestra (véase Aliasing ). El límite de frecuencia correspondiente, en ciclos por segundo ( hertz ), es ciclo/muestra × muestras/segundo = , conocida como la frecuencia de Nyquist del muestreador. Por lo tanto, suele ser la salida de un filtro de paso bajo , conocido funcionalmente como filtro anti-aliasing . Sin un filtro anti-aliasing, las frecuencias superiores a la frecuencia de Nyquist influirán en las muestras de una forma que será malinterpretada por el proceso de interpolación. [4]
Consideraciones prácticas
En la práctica, la señal continua se muestrea mediante un convertidor analógico a digital (ADC), un dispositivo con varias limitaciones físicas. Esto da como resultado desviaciones de la reconstrucción teóricamente perfecta, denominadas colectivamente como distorsión .
Pueden ocurrir varios tipos de distorsión, entre ellos:
- Aliasing . Es inevitable que se produzca cierto grado de aliasing, ya que solo las funciones teóricas, infinitamente largas, pueden no tener un contenido de frecuencia superior a la frecuencia de Nyquist. El aliasing se puede reducir de forma arbitraria utilizando un orden suficientemente grande del filtro antialiasing.
- El error de apertura resulta del hecho de que la muestra se obtiene como un promedio temporal dentro de una región de muestreo, en lugar de ser simplemente igual al valor de la señal en el instante de muestreo. [5] En un circuito de muestreo y retención basado en capacitores , los errores de apertura se introducen por múltiples mecanismos. Por ejemplo, el capacitor no puede rastrear instantáneamente la señal de entrada y no puede aislarse instantáneamente de la señal de entrada.
- Fluctuación o desviación de los intervalos de tiempo de muestra precisos.
- Ruido , incluido ruido del sensor térmico, ruido del circuito analógico , etc.
- Error de límite de velocidad de respuesta , causado por la incapacidad del valor de entrada del ADC de cambiar con la suficiente rapidez.
- Cuantización como consecuencia de la precisión finita de las palabras que representan los valores convertidos.
- Error debido a otros efectos no lineales del mapeo del voltaje de entrada al valor de salida convertido (además de los efectos de la cuantificación).
Aunque el uso del sobremuestreo puede eliminar por completo el error de apertura y el aliasing al desplazarlos fuera de la banda de paso, esta técnica no se puede utilizar en la práctica por encima de unos pocos GHz y puede resultar prohibitivamente cara a frecuencias mucho más bajas. Además, aunque el sobremuestreo puede reducir el error de cuantificación y la no linealidad, no puede eliminarlos por completo. En consecuencia, los ADC prácticos en frecuencias de audio normalmente no presentan aliasing, error de apertura y no están limitados por el error de cuantificación. En cambio, predomina el ruido analógico. En frecuencias de RF y microondas donde el sobremuestreo es poco práctico y los filtros son caros, el error de apertura, el error de cuantificación y el aliasing pueden ser limitaciones significativas.
El jitter, el ruido y la cuantificación se suelen analizar modelándolos como errores aleatorios añadidos a los valores de muestra. Los efectos de integración y retención de orden cero se pueden analizar como una forma de filtrado de paso bajo . Las no linealidades de los convertidores analógico-digitales (ADC) o analógico-digitales (DAC) se analizan reemplazando la función lineal ideal por una función no lineal propuesta .
Aplicaciones
Muestreo de audio
El audio digital utiliza modulación por código de pulsos (PCM) y señales digitales para la reproducción de sonido. Esto incluye la conversión de analógico a digital (ADC), la conversión de digital a analógico (DAC), el almacenamiento y la transmisión. En efecto, el sistema al que comúnmente se hace referencia como digital es, de hecho, un análogo discreto en tiempo y nivel de un análogo eléctrico anterior. Si bien los sistemas modernos pueden ser bastante sutiles en sus métodos, la principal utilidad de un sistema digital es la capacidad de almacenar, recuperar y transmitir señales sin ninguna pérdida de calidad.
Cuando es necesario capturar audio que cubra todo el rango de 20 a 20 000 Hz de la audición humana [6], como cuando se graba música o muchos tipos de eventos acústicos, las formas de onda de audio se muestrean típicamente a 44,1 kHz ( CD ), 48 kHz, 88,2 kHz o 96 kHz. [7] El requisito de aproximadamente el doble de frecuencia es una consecuencia del teorema de Nyquist . Las frecuencias de muestreo superiores a aproximadamente 50 kHz a 60 kHz no pueden proporcionar más información utilizable para los oyentes humanos. Los primeros fabricantes de equipos de audio profesionales eligieron frecuencias de muestreo en la región de 40 a 50 kHz por este motivo.
Ha habido una tendencia en la industria hacia frecuencias de muestreo mucho más allá de los requisitos básicos: como 96 kHz e incluso 192 kHz [8] Aunque las frecuencias ultrasónicas son inaudibles para los humanos, la grabación y mezcla a frecuencias de muestreo más altas es eficaz para eliminar la distorsión que puede ser causada por el aliasing de retroceso . Por el contrario, los sonidos ultrasónicos pueden interactuar con y modular la parte audible del espectro de frecuencia ( distorsión de intermodulación ), degradando la fidelidad. [9] Una ventaja de las frecuencias de muestreo más altas es que pueden relajar los requisitos de diseño de filtro de paso bajo para ADC y DAC , pero con los modernos convertidores delta-sigma de sobremuestreo esta ventaja es menos importante.
La Audio Engineering Society recomienda una frecuencia de muestreo de 48 kHz para la mayoría de las aplicaciones, pero reconoce 44,1 kHz para CD y otros usos de consumo, 32 kHz para aplicaciones relacionadas con la transmisión y 96 kHz para un mayor ancho de banda o un filtrado anti-aliasing relajado . [10] Tanto Lavry Engineering como J. Robert Stuart afirman que la frecuencia de muestreo ideal sería de unos 60 kHz, pero como no es una frecuencia estándar, recomiendan 88,2 o 96 kHz para fines de grabación. [11] [12] [13] [14]
Una lista más completa de frecuencias de muestreo de audio comunes es:
| Frecuencia de muestreo | Usar |
|---|---|
| 8.000 Hz | Teléfono y walkie-talkie encriptado , intercomunicador inalámbrico y transmisión por micrófono inalámbrico ; adecuado para el habla humana pero sin sibilancia ( ess suena como eff ( / s / , / f / )). |
| 11.025 Hz | Una cuarta parte de la frecuencia de muestreo de los CD de audio; se utiliza para audio PCM y MPEG de menor calidad y para el análisis de audio de los pasos de banda de subwoofer. [ cita requerida ] |
| 16.000 Hz | Extensión de frecuencia de banda ancha sobre la banda estrecha telefónica estándar de 8000 Hz. Se utiliza en la mayoría de los productos de comunicación VoIP y VVoIP modernos. [15] [ ¿ Fuente poco confiable? ] |
| 22.050 Hz | La mitad de la frecuencia de muestreo de los CD de audio; se utiliza para audio PCM y MPEG de menor calidad y para análisis de audio de energía de baja frecuencia. Adecuado para digitalizar formatos de audio de principios del siglo XX, como los de 78 rpm y la radio AM . [16] |
| 32.000 Hz | videocámara digital miniDV , cintas de video con canales de audio adicionales (por ejemplo, DVCAM con cuatro canales de audio), DAT (modo LP), radio satelital digital alemana, audio digital NICAM , utilizado junto con el sonido de televisión analógica en algunos países. Micrófonos inalámbricos digitales de alta calidad . [17] Adecuado para digitalizar radio FM . [ cita requerida ] |
| 37.800 Hz | Audio en CD-XA |
| 44.056 Hz | Utilizado por audio digital bloqueado en señales de video en color NTSC (3 muestras por línea, 245 líneas por campo, 59,94 campos por segundo = 29,97 cuadros por segundo ). |
| 44.100 Hz | CD de audio , también más comúnmente utilizado con audio MPEG-1 ( VCD , SVCD , MP3 ). Originalmente elegido por Sony porque podía grabarse en equipos de video modificados que funcionaran a 25 cuadros por segundo (PAL) o 30 cuadros por segundo (usando una grabadora de video monocromática NTSC ) y cubrir el ancho de banda de 20 kHz que se creía necesario para que coincidiera con el equipo de grabación analógico profesional de la época. Un adaptador PCM encajaría muestras de audio digital en el canal de video analógico de, por ejemplo, cintas de video PAL usando 3 muestras por línea, 588 líneas por cuadro, 25 cuadros por segundo. |
| 47.250 Hz | El primer grabador de sonido PCM comercial del mundo de Nippon Columbia (Denon) |
| 48.000 Hz | Frecuencia de muestreo de audio estándar utilizada por equipos de video digital profesionales, como grabadoras de cinta, servidores de video, mezcladores de visión, etc. Se eligió esta frecuencia porque podía reconstruir frecuencias de hasta 22 kHz y funcionar con video NTSC de 29,97 cuadros por segundo, así como con sistemas de 25 cuadros/s, 30 cuadros/s y 24 cuadros/s. Con sistemas de 29,97 cuadros/s es necesario manejar 1601,6 muestras de audio por cuadro, entregando un número entero de muestras de audio solo cada quinto cuadro de video. [10] También se usa para sonido con formatos de video de consumo como DV, TV digital , DVD y películas. La interfaz digital en serie profesional (SDI) y la interfaz digital en serie de alta definición (HD-SDI) que se usan para conectar equipos de televisión de transmisión usan esta frecuencia de muestreo de audio. La mayoría de los equipos de audio profesionales usan un muestreo de 48 kHz, incluidas las consolas de mezcla y los dispositivos de grabación digital . |
| 50.000 Hz | Primeras grabadoras de audio digitales comerciales de finales de los años 70 de 3M y Soundstream . |
| 50.400 Hz | Frecuencia de muestreo utilizada por la grabadora de audio digital Mitsubishi X-80 . |
| 64.000 Hz | De uso poco común, pero compatible con algunos hardware [18] [19] y software. [20] [21] |
| 88.200 Hz | Frecuencia de muestreo utilizada por algunos equipos de grabación profesionales cuando el destino es un CD (múltiplos de 44.100 Hz). Algunos equipos de audio profesionales utilizan (o pueden seleccionar) un muestreo de 88,2 kHz, incluidos mezcladores, ecualizadores, compresores, reverberaciones, filtros de cruce y dispositivos de grabación. |
| 96.000 Hz | DVD-Audio , algunas pistas de DVD LPCM , pistas de audio de BD-ROM (disco Blu-ray), pistas de audio de HD DVD (DVD de alta definición). Algunos equipos de grabación y producción profesionales pueden seleccionar un muestreo de 96 kHz. Esta frecuencia de muestreo es el doble del estándar de 48 kHz que se utiliza habitualmente con el audio en equipos profesionales. |
| 176.400 Hz | Frecuencia de muestreo utilizada por grabadoras HDCD y otras aplicaciones profesionales para la producción de CD. Cuatro veces la frecuencia de 44,1 kHz. |
| 192.000 Hz | DVD-Audio , algunas pistas de DVD LPCM , pistas de audio de BD-ROM (disco Blu-ray) y pistas de audio de HD DVD (DVD de alta definición), dispositivos de grabación de audio de alta definición y software de edición de audio. Esta frecuencia de muestreo es cuatro veces el estándar de 48 kHz que se utiliza habitualmente con el audio en equipos de vídeo profesionales. |
| 352.800 Hz | Definición Digital eXtreme , utilizada para grabar y editar Super Audio CD , ya que Direct Stream Digital (DSD) de 1 bit no es adecuado para la edición. 8 veces la frecuencia de 44,1 kHz. |
| 2.822.400 Hz | SACD , proceso de modulación delta-sigma de 1 bit conocido como Direct Stream Digital , desarrollado conjuntamente por Sony y Philips . |
| 5.644.800 Hz | DSD de doble velocidad, transmisión digital directa de 1 bit a una velocidad dos veces superior a la del SACD. Se utiliza en algunas grabadoras DSD profesionales. |
| 11.289.600 Hz | DSD de cuatro velocidades, transmisión digital directa de 1 bit a una velocidad cuatro veces superior a la del SACD. Se utiliza en algunas grabadoras DSD profesionales poco comunes. |
| 22.579.200 Hz | DSD de frecuencia óctuple, transmisión digital directa de 1 bit a una frecuencia 8 veces superior a la del SACD. Se utiliza en grabadoras DSD experimentales poco comunes. También se conoce como DSD512. |
| 45.158.400 Hz | DSD de frecuencia sexdecuple, flujo directo digital de 1 bit a una frecuencia 16 veces mayor que la del SACD. Se utiliza en grabadoras DSD experimentales poco comunes. También se conoce como DSD1024. [B] |
Profundidad de bits
El audio se graba típicamente a una profundidad de 8, 16 y 24 bits, lo que produce una relación señal-ruido de cuantificación (SQNR) máxima teórica para una onda sinusoidal pura de, aproximadamente, 49,93 dB , 98,09 dB y 122,17 dB. [22] El audio con calidad de CD utiliza muestras de 16 bits. El ruido térmico limita la cantidad real de bits que se pueden usar en la cuantificación. Pocos sistemas analógicos tienen relaciones señal-ruido (SNR) que superen los 120 dB. Sin embargo, las operaciones de procesamiento de señales digitales pueden tener un rango dinámico muy alto, por lo que es común realizar operaciones de mezcla y masterización con una precisión de 32 bits y luego convertir a 16 o 24 bits para su distribución.
Muestreo de voz
Las señales de voz, es decir, las señales destinadas a transmitir únicamente el habla humana , normalmente se pueden muestrear a una velocidad mucho menor. Para la mayoría de los fonemas , casi toda la energía está contenida en el rango de 100 Hz a 4 kHz, lo que permite una velocidad de muestreo de 8 kHz. Esta es la velocidad de muestreo utilizada por casi todos los sistemas de telefonía , que utilizan las especificaciones de muestreo y cuantificación G.711 . [ cita requerida ]
Muestreo de video
Esta sección necesita citas adicionales para su verificación . ( Junio de 2007 ) |
La televisión de definición estándar (SDTV) utiliza 720 por 480 píxeles ( NTSC de EE. UU. de 525 líneas) o 720 por 576 píxeles ( PAL del Reino Unido de 625 líneas) para el área de imagen visible.
La televisión de alta definición (HDTV) utiliza 720p (progresivo), 1080i (entrelazado) y 1080p (progresivo, también conocido como Full-HD).
En el vídeo digital , la frecuencia de muestreo temporal se define como la frecuencia de cuadros (o más bien, la frecuencia de campo ) en lugar del reloj de píxeles teórico. La frecuencia de muestreo de la imagen es la tasa de repetición del período de integración del sensor. Dado que el período de integración puede ser significativamente más corto que el tiempo entre repeticiones, la frecuencia de muestreo puede ser diferente de la inversa del tiempo de muestreo:
Los convertidores de video digital a analógico operan en el rango de megahercios (desde ~3 MHz para escaladores de video compuesto de baja calidad en las primeras consolas de juegos, hasta 250 MHz o más para la salida VGA de mayor resolución).
Cuando el vídeo analógico se convierte en vídeo digital , se produce un proceso de muestreo diferente, esta vez en la frecuencia de píxeles, correspondiente a una frecuencia de muestreo espacial a lo largo de las líneas de exploración . Una frecuencia de muestreo de píxeles común es:
El muestreo espacial en la otra dirección está determinado por el espaciado de las líneas de escaneo en la trama . Las velocidades de muestreo y las resoluciones en ambas direcciones espaciales se pueden medir en unidades de líneas por altura de imagen.
El aliasing espacial de los componentes de vídeo de luminancia o croma de alta frecuencia se muestra como un patrón muaré .
Muestreo 3D
El proceso de renderización de volumen toma muestras de una cuadrícula 3D de vóxeles para producir representaciones 3D de datos en rodajas (tomográficos). Se supone que la cuadrícula 3D representa una región continua del espacio 3D. La renderización de volumen es común en imágenes médicas; la tomografía computarizada con rayos X (TC/CAT), la resonancia magnética (IRM) y la tomografía por emisión de positrones (PET) son algunos ejemplos. También se utiliza para la tomografía sísmica y otras aplicaciones.

Submuestreo
Cuando una señal de paso de banda se muestrea más lentamente que su tasa de Nyquist , las muestras son indistinguibles de las muestras de un alias de baja frecuencia de la señal de alta frecuencia. Esto se hace a menudo a propósito de tal manera que el alias de frecuencia más baja satisface el criterio de Nyquist , porque la señal de paso de banda todavía está representada de manera única y es recuperable. Este submuestreo también se conoce como muestreo de paso de banda , muestreo armónico , muestreo de FI y conversión directa de FI a digital. [23]
Sobremuestreo
El sobremuestreo se utiliza en la mayoría de los convertidores analógico-digitales modernos para reducir la distorsión introducida por los convertidores digitales-analógicos prácticos , como una retención de orden cero en lugar de idealizaciones como la fórmula de interpolación de Whittaker-Shannon . [24]
Muestreo complejo
El muestreo complejo (o muestreo I/Q ) es el muestreo simultáneo de dos formas de onda diferentes, pero relacionadas, lo que da como resultado pares de muestras que posteriormente se tratan como números complejos . [C] Cuando una forma de onda, , es la transformada de Hilbert de la otra forma de onda, , la función de valor complejo, , se denomina señal analítica , cuya transformada de Fourier es cero para todos los valores negativos de frecuencia. En ese caso, la tasa de Nyquist para una forma de onda sin frecuencias ≥ B se puede reducir a solo B (muestras complejas/seg), en lugar de (muestras reales/seg). [D] De manera más aparente, la forma de onda de banda base equivalente , , también tiene una tasa de Nyquist de , porque todo su contenido de frecuencia distinto de cero se desplaza al intervalo .
Aunque las muestras de valor complejo se pueden obtener como se describió anteriormente, también se crean manipulando muestras de una forma de onda de valor real. Por ejemplo, la forma de onda de banda base equivalente se puede crear sin calcular explícitamente , procesando la secuencia de producto, , [E] a través de un filtro de paso bajo digital cuya frecuencia de corte es . [F] Calcular solo cada dos muestras de la secuencia de salida reduce la frecuencia de muestreo proporcional a la frecuencia de Nyquist reducida. El resultado es la mitad de muestras de valor complejo que el número original de muestras reales. No se pierde información y se puede recuperar la forma de onda original, si es necesario.
Véase también
- Frecuencias del oscilador de cristal
- Reducción de muestreo
- Muestreo ascendente
- Muestreo multidimensional
- Componentes en fase y en cuadratura y datos I/Q
- Conversión de frecuencia de muestreo
- Digitalización
- Muestrear y mantener
- Codificador beta
- Factor Kell
- Tasa de bits
- Frecuencia normalizada
Notas
- ^ Por ejemplo, "número de muestras" en el procesamiento de señales es aproximadamente equivalente a " tamaño de muestra " en estadística.
- ^ Existen frecuencias de muestreo DSD incluso más altas, pero sus beneficios probablemente sean imperceptibles y el tamaño de esos archivos sería enorme.
- ^ Los pares de muestras a veces también se consideran puntos en un diagrama de constelación .
- ^ Cuando la frecuencia de muestreo compleja es B , un componente de frecuencia en 0,6 B , por ejemplo, tendrá un alias en −0,4 B , lo cual es inequívoco debido a la restricción de que la señal premuestreada era analítica. Véase también Aliasing § Sinusoides complejas .
- ^ Cuando s ( t ) se muestrea en la frecuencia de Nyquist (1/ T = 2 B ), la secuencia del producto se simplifica a
- ^ La secuencia de números complejos se convoluciona con la respuesta al impulso de un filtro con coeficientes de valor real. Esto equivale a filtrar por separado las secuencias de partes reales y partes imaginarias y reformar pares complejos en las salidas.
Referencias
- ^ Martin H. Weik (1996). Diccionario estándar de comunicaciones. Springer. ISBN 0412083914.
- ^ Tom J. Moir (2022). Rudimentos de procesamiento de señales y sistemas. Springer International Publishing AG. pág. 459. doi :10.1007/978-3-030-76947-5. ISBN 9783030769475.
- ^ Rao, R. (2008). Señales y sistemas. Prentice-Hall Of India Pvt. Limited. ISBN 9788120338593.
- ^ CE Shannon , "Comunicación en presencia de ruido", Proc. Institute of Radio Engineers , vol. 37, n.º 1, págs. 10-21, enero de 1949. Reimpresión como artículo clásico en: Proc. IEEE, vol. 86, n.º 2, (febrero de 1998) Archivado el 8 de febrero de 2010 en Wayback Machine.
- ^ HO Johansson y C. Svensson, "Resolución temporal de conmutadores de muestreo NMOS", IEEE J. Solid-State Circuits Volumen: 33, Número: 2, págs. 237–245, febrero de 1998.
- ^ D'Ambrose, Christoper; Choudhary, Rizwan (2003). Elert, Glenn (ed.). "Rango de frecuencia de la audición humana". The Physics Factbook . Consultado el 22 de enero de 2022 .
- ^ Self, Douglas (2012). Ingeniería de audio explicada. Taylor & Francis US. págs. 200, 446. ISBN 978-0240812731.
- ^ "Digital Pro Sound" . Consultado el 8 de enero de 2014 .
- ^ Colletti, Justin (4 de febrero de 2013). "La ciencia de las frecuencias de muestreo (cuándo una frecuencia más alta es mejor y cuándo no)". Trust Me I'm a Scientist ( Confía en mí, soy un científico) . Consultado el 6 de febrero de 2013.
En muchos casos, podemos oír el sonido de frecuencias de muestreo más altas no porque sean más transparentes, sino porque lo son menos. En realidad, pueden introducir una distorsión no deseada en el espectro audible.
- ^ ab AES5-2008: Práctica recomendada por AES para audio digital profesional: frecuencias de muestreo preferidas para aplicaciones que emplean modulación por código de pulsos, Audio Engineering Society, 2008 , consultado el 18 de enero de 2010
- ^ Lavry, Dan (3 de mayo de 2012). "La frecuencia de muestreo óptima para un audio de calidad" (PDF) . Lavry Engineering Inc. Aunque
60 KHz estaría más cerca del ideal, dadas las normas existentes, 88,2 KHz y 96 KHz son las frecuencias de muestreo más cercanas a la óptima.
- ^ Lavry, Dan. "La frecuencia de muestreo óptima para un audio de calidad". Gearslutz . Consultado el 10 de noviembre de 2018. Estoy
intentando adaptarme a todos los oídos y hay informes de pocas personas que realmente pueden escuchar ligeramente por encima de los 20 KHz. Creo que 48 KHz es un compromiso bastante bueno, pero 88,2 o 96 KHz ofrecen un margen adicional.
- ^ Lavry, Dan. "¿Mezclar a 96k o no?". Gearslutz . Consultado el 10 de noviembre de 2018. Hoy en día ,
hay una serie de buenos diseñadores y personas que se preocupan por el oído que consideran que la frecuencia de muestreo de 60-70 KHz es la frecuencia óptima para el oído. Es lo suficientemente rápida para incluir lo que podemos escuchar, pero lo suficientemente lenta para hacerlo con bastante precisión.
- ^ Stuart, J. Robert (1998). Codificación de audio digital de alta calidad . CiteSeerX 10.1.1.501.6731 .
Tanto el análisis psicoacústico como la experiencia nos indican que el canal rectangular mínimo necesario para garantizar la transparencia utiliza PCM lineal con muestras de 18,2 bits a 58 kHz. ... existen argumentos sólidos para mantener las relaciones de números enteros con las frecuencias de muestreo existentes, lo que sugiere que se deberían adoptar 88,2 kHz o 96 kHz.
- ^ "Teléfonos VoIP de Cisco, redes y accesorios - Suministro de VoIP".
- ^ "El procedimiento de restauración – parte 1". Restoring78s.co.uk. Archivado desde el original el 14 de septiembre de 2009. Consultado el 18 de enero de 2011.
Para la mayoría de los discos, una frecuencia de muestreo de 22050 en estéreo es adecuada. Es probable que una excepción sean las grabaciones realizadas en la segunda mitad del siglo, que pueden necesitar una frecuencia de muestreo de 44100.
- ^ "Transmisores inalámbricos digitales Zaxcom". Zaxcom.com. Archivado desde el original el 2011-02-09 . Consultado el 2011-01-18 .
- ^ "RME: Hammerfall DSP 9632". www.rme-audio.de . Consultado el 18 de diciembre de 2018 .
Frecuencias de muestreo admitidas: internamente 32, 44,1, 48, 64, 88,2, 96, 176,4, 192 kHz.
- ^ "SX-S30DAB | Pioneer". www.pioneer-audiovisual.eu . Consultado el 18 de diciembre de 2018 .
Frecuencias de muestreo admitidas: 44,1 kHz, 48 kHz, 64 kHz, 88,2 kHz, 96 kHz, 176,4 kHz, 192 kHz
- ^ Cristina Bachmann, Heiko Bischoff; Schütte, Benjamin. "Menú de personalización de frecuencia de muestreo". Steinberg WaveLab Pro . Consultado el 18 de diciembre de 2018.
Frecuencias de muestreo habituales: 64 000 Hz
- ^ "M Track 2x2M Cubase Pro 9 no puede cambiar la frecuencia de muestreo". M-Audio . Consultado el 18 de diciembre de 2018 .
[Captura de pantalla de Cubase]
- ^ "MT-001: Desmitificando la infame fórmula "SNR=6,02N + 1,76dB" y por qué debería importarte" (PDF) .
- ^ Walt Kester (2003). Técnicas de diseño de señales mixtas y DSP. Newnes. p. 20. ISBN 978-0-7506-7611-3. Recuperado el 8 de enero de 2014 .
- ^ William Morris Hartmann (1997). Señales, sonido y sensación. Springer. ISBN 1563962837.
Lectura adicional
- Matt Pharr, Wenzel Jakob y Greg Humphreys, Physically Based Rendering: From Theory to Implementation, 3.ª ed. , Morgan Kaufmann, noviembre de 2016. ISBN 978-0128006450 . El capítulo sobre muestreo (disponible en línea) está muy bien escrito, con diagramas, teoría básica y ejemplos de código.
Enlaces externos
- Revista dedicada a la teoría del muestreo
- Datos I/Q para principiantes: una página que intenta responder a la pregunta ¿Por qué datos I/Q?
- Muestreo de señales analógicas: una presentación interactiva en una demostración web en el Instituto de Telecomunicaciones de la Universidad de Stuttgart















![{\estilo de visualización [-B/2,B/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eaba70af89480aab78d7c35025882696835bcb7)
![{\displaystyle \left[s(nT)\cdot e^{-i2\pi {\frac {B}{2}}Tn}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ae973e6561275c7668442cbdd54557d6a377cec)

![{\displaystyle \left[s(nT)\cdot (-i)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e0394ce8648cfa875d6274242b21368a4ded905)