Interferómetro de Fabry-Pérot

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Interferómetro de Fabry-Pérot» – noticias  · periódicos  · libros  · académico  · JSTOR ( mayo de 2016 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En óptica , un interferómetro Fabry-Pérot ( FPI ) o etalón es una cavidad óptica hecha de dos superficies reflectantes paralelas (es decir, espejos delgados ). Las ondas ópticas pueden pasar a través de la cavidad óptica solo cuando están en resonancia con ella. Recibe su nombre en honor a Charles Fabry y Alfred Perot , quienes desarrollaron el instrumento en 1899. ^{[1] [2] [3]} Etalon proviene del francés étalon , que significa "calibre de medición" o "estándar". ^[4]

Los etalones se utilizan ampliamente en telecomunicaciones , láseres y espectroscopia para controlar y medir las longitudes de onda de la luz. Los recientes avances en la técnica de fabricación permiten la creación de interferómetros Fabry-Pérot sintonizables muy precisos. El dispositivo es técnicamente un interferómetro cuando la distancia entre las dos superficies (y con ello la longitud de resonancia) se puede cambiar, y un etalón cuando la distancia es fija (sin embargo, los dos términos se usan a menudo indistintamente).

El corazón del interferómetro Fabry-Pérot es un par de planos ópticos de vidrio parcialmente reflectantes espaciados entre micrómetros y centímetros, con las superficies reflectantes enfrentadas. (Alternativamente, un etalón Fabry-Pérot utiliza una sola placa con dos superficies reflectantes paralelas). Los planos de un interferómetro suelen estar hechos en forma de cuña para evitar que las superficies traseras produzcan franjas de interferencia; las superficies traseras a menudo también tienen un revestimiento antirreflectante .

En un sistema típico, la iluminación es proporcionada por una fuente difusa situada en el plano focal de una lente colimadora . Una lente de enfoque después del par de planos produciría una imagen invertida de la fuente si los planos no estuvieran presentes; toda la luz emitida desde un punto de la fuente se enfoca en un solo punto en el plano de imagen del sistema. En la ilustración adjunta, solo se traza un rayo emitido desde el punto A en la fuente. A medida que el rayo pasa a través de los planos emparejados, se refleja repetidamente para producir múltiples rayos transmitidos que son recogidos por la lente de enfoque y llevados al punto A' en la pantalla. El patrón de interferencia completo toma la apariencia de un conjunto de anillos concéntricos. La nitidez de los anillos depende de la reflectividad de los planos. Si la reflectividad es alta, lo que resulta en un factor Q alto , la luz monocromática produce un conjunto de anillos brillantes estrechos contra un fondo oscuro. Se dice que un interferómetro de Fabry-Pérot con Q alto tiene alta fineza .

Las redes de telecomunicaciones que emplean multiplexación por división de longitud de onda tienen multiplexores de inserción y extracción con bancos de etalones de diamante o sílice fundido sintonizados en miniatura . Se trata de pequeños cubos iridiscentes de unos 2 mm de lado, montados en pequeños bastidores de alta precisión. Los materiales se eligen para mantener distancias estables entre espejos y frecuencias estables incluso cuando varía la temperatura. Se prefiere el diamante porque tiene una mayor conducción del calor y aún tiene un bajo coeficiente de expansión. En 2005, algunas empresas de equipos de telecomunicaciones comenzaron a utilizar etalones sólidos que son en sí mismos fibras ópticas. Esto elimina la mayoría de las dificultades de montaje, alineación y refrigeración.

Los filtros dicroicos se fabrican depositando una serie de capas etalónicas sobre una superficie óptica mediante deposición de vapor . Estos filtros ópticos suelen tener bandas de reflexión y paso más exactas que los filtros absorbentes. Cuando están diseñados correctamente, funcionan a menor temperatura que los filtros absorbentes porque reflejan longitudes de onda no deseadas en lugar de absorberlas. Los filtros dicroicos se utilizan ampliamente en equipos ópticos como fuentes de luz, cámaras, equipos astronómicos y sistemas láser.

Los medidores de ondas ópticos y algunos analizadores de espectro óptico utilizan interferómetros Fabry-Pérot con diferentes rangos espectrales libres para determinar la longitud de onda de la luz con gran precisión.

Los resonadores láser se describen a menudo como resonadores Fabry-Pérot, aunque para muchos tipos de láser la reflectividad de un espejo es cercana al 100%, lo que lo hace más similar a un interferómetro de Gires-Tournois . Los láseres de diodo semiconductor a veces utilizan una verdadera geometría Fabry-Pérot, debido a la dificultad de recubrir las facetas finales del chip. Los láseres de cascada cuántica a menudo emplean cavidades Fabry-Pérot para sostener la emisión láser sin la necesidad de ningún recubrimiento de facetas, debido a la alta ganancia de la región activa. ^[5]

Los etalones se colocan a menudo dentro del resonador láser cuando se construyen láseres monomodo. Sin un etalón, un láser generalmente producirá luz en un rango de longitud de onda correspondiente a una serie de modos de cavidad , que son similares a los modos Fabry-Pérot. Insertar un etalón en la cavidad láser, con una delicadeza bien elegida y un rango espectral libre, puede suprimir todos los modos de cavidad excepto uno, cambiando así el funcionamiento del láser de multimodo a monomodo.

Los interferómetros Fabry-Pérot estables se utilizan a menudo para estabilizar la frecuencia de la luz emitida por un láser (que a menudo fluctúa debido a vibraciones mecánicas o cambios de temperatura) mediante el bloqueo de la misma en un modo de la cavidad. Existen muchas técnicas para producir una señal de error, como la técnica de Pound-Drever-Hall, ampliamente utilizada .

Los etalones de Fabry-Pérot se pueden utilizar para prolongar la longitud de interacción en la espectrometría de absorción láser , en particular en las técnicas de cavidad ring-down . Un etalón de espesor creciente se puede utilizar como filtro óptico lineal variable para lograr espectroscopia . Se puede hacer increíblemente pequeño utilizando películas delgadas de espesores nanométricos. ^[6]

Se puede utilizar un etalón de Fabry-Pérot para fabricar un espectrómetro capaz de observar el efecto Zeeman , donde las líneas espectrales están demasiado juntas para distinguirlas con un espectrómetro normal.

En astronomía, se utiliza un etalón para seleccionar una única transición atómica para la toma de imágenes. La más común es la línea H-alfa del Sol . La línea Ca-K del Sol también se suele fotografiar con etalones.

El sensor de metano para Marte (MSM) a bordo de la sonda india Mangalyaan es un ejemplo de instrumento Fabry-Pérot. Fue el primer instrumento Fabry-Pérot en el espacio cuando se lanzó el Mangalyaan. ^[7] Como no distinguía la radiación absorbida por el metano de la radiación absorbida por el dióxido de carbono y otros gases, más tarde se lo denominó mapeador de albedo. ^[8]

En la detección de ondas gravitacionales , se utiliza una cavidad Fabry-Pérot para almacenar fotones durante casi un milisegundo mientras rebotan hacia arriba y hacia abajo entre los espejos. Esto aumenta el tiempo que una onda gravitacional puede interactuar con la luz, lo que resulta en una mejor sensibilidad a bajas frecuencias. Este principio es utilizado por detectores como LIGO y Virgo , que consisten en un interferómetro de Michelson con una cavidad Fabry-Pérot con una longitud de varios kilómetros en ambos brazos. Cavidades más pequeñas, generalmente llamadas limpiadores de modos , se utilizan para el filtrado espacial y la estabilización de frecuencia del láser principal. ^[9]

La respuesta espectral de un resonador Fabry-Pérot se basa en la interferencia entre la luz que se lanza hacia él y la luz que circula en el resonador. La interferencia constructiva se produce si los dos haces están en fase , lo que provoca un aumento resonante de la luz dentro del resonador. Si los dos haces están desfasados, solo una pequeña parte de la luz lanzada se almacena dentro del resonador. La luz almacenada, transmitida y reflejada se modifica espectralmente en comparación con la luz incidente.

Supongamos un resonador Fabry-Pérot de dos espejos de longitud geométrica , homogéneamente lleno con un medio de índice de refracción . La luz se lanza al resonador bajo incidencia normal. El tiempo de ida y vuelta de la luz que viaja en el resonador con velocidad , donde es la velocidad de la luz en el vacío, y el rango espectral libre están dados por${\displaystyle \ell}$${\estilo de visualización n}$${\displaystyle t_{\rm {RT}}}$$estilo de visualización c=c_{0}/n$$estilo de visualización c_{0}}$ ${\displaystyle \Delta \nu _ {\rm {FSR}}}$

${\displaystyle t_{\rm {RT}}={\frac {1}{\Delta \nu _{\rm {FSR}}}}={\frac {2\ell }{c}}.}$

Las reflectividades del campo eléctrico y de la intensidad y , respectivamente, en el espejo son${\displaystyle r_{i}}$${\displaystyle R_{i}}$${\estilo de visualización i}$

${\displaystyle |r_{i}|^{2}=R_{i}.}$

Si no hay otras pérdidas del resonador, la disminución de la intensidad de la luz por cada viaje de ida y vuelta se cuantifica mediante la constante de tasa de disminución del acoplamiento.${\displaystyle 1/\tau _{\rm {fuera}},}$

${\displaystyle R_{1}R_{2}=e^{-t_{\rm {RT}}/\tau _{\rm {salida}}},}$

y el tiempo de desintegración del fotón del resonador se expresa entonces mediante ^[10]${\displaystyle \tau_{c}}$

${\displaystyle {\frac {1}{\tau _{c}}}={\frac {1}{\tau _{\rm {salida}}}}={\frac {-\ln {(R_{1}R_{2})}}{t_{\rm {RT}}}}.}$

Al cuantificar el cambio de fase de un solo paso que exhibe la luz al propagarse de un espejo al otro, el cambio de fase de ida y vuelta en la frecuencia se acumula en ^[10]${\displaystyle \phi (\nu )}$${\estilo de visualización \nu}$

${\displaystyle 2\phi (\nu )=2\pi \nu t_{\rm {RT}}.}$

Las resonancias se producen en frecuencias en las que la luz presenta interferencia constructiva después de un viaje de ida y vuelta. Cada modo de resonador con su índice de modo , donde es un entero en el intervalo , está asociado con una frecuencia de resonancia y un número de onda ,${\estilo de visualización q}$${\estilo de visualización q}$${\displaystyle [-\infty,\infty]}$${\displaystyle \nu_{q}}$$estilo de visualización k_{q}}$

${\displaystyle \nu_{q}=q\Delta \nu_{\rm {FSR}}\Rightarrow k_{q}={\frac {2\pi q\Delta \nu_{\rm {FSR}}}{c}}.}$

Dos modos con valores opuestos de índice modal y número de onda, respectivamente, que representan físicamente direcciones de propagación opuestas, ocurren en el mismo valor absoluto de frecuencia. ^[11]${\displaystyle \pm q}$${\displaystyle \pm k}$${\displaystyle \izquierda|\nu _{q}\derecha|}$

El campo eléctrico en decaimiento a frecuencia se representa mediante una oscilación armónica amortiguada con una amplitud inicial de y una constante de tiempo de decaimiento de . En notación fasorial, se puede expresar como ^[10]${\displaystyle \nu_{q}}$${\displaystyle E_{q,s}}$${\displaystyle 2\tau_{c}}$

${\displaystyle E_{q}(t)=E_{q,s}e^{i2\pi \nu _{q}t}e^{-{\frac {t}{2\tau _{c}}}}.}$

La transformada de Fourier del campo eléctrico en el tiempo proporciona el campo eléctrico por intervalo de frecuencia unitario,

${\displaystyle {\tilde {E}}_{q}(\nu )=\int _{-\infty }^{+\infty }E_{q}(t)e^{-i2\pi \nu t}\,dt=E_{q,s}{\frac {1}{(2\tau _{c})^{-1}+i2\pi (\nu -\nu _{q})}}.}$

Cada modo tiene una forma de línea espectral normalizada por intervalo de frecuencia unitario dada por

${\displaystyle {\tilde {\gamma }}_{q}(\nu )={\frac {1}{\tau _{c}}}\left|{\frac {{\tilde {E}}_{q}(\nu )}{E_{q,s}}}\right|^{2}={\frac {1}{\tau _{c}}}{\frac {1}{(2\tau _{c})^{-2}+4\pi ^{2}(\nu -\nu _{q})^{2}}},}$

cuya integral de frecuencia es la unidad. Introduciendo el ancho completo a la mitad del ancho máximo (FWHM) de la línea espectral de Lorentz, obtenemos${\displaystyle \Delta \nu _{c}}$

${\displaystyle \Delta \nu _{c}={\frac {1}{2\pi \tau _{c}}}\Rightarrow {\tilde {\gamma }}_{q}(\nu )={\frac {1}{\pi }}{\frac {\Delta \nu _{c}/2}{(\Delta \nu _{c}/2)^{2}+(\nu -\nu _{q})^{2}}}={\frac {2}{\pi }}{\frac {\Delta \nu _{c}}{(\Delta \nu _{c})^{2}+4(\nu -\nu _{q})^{2}}},}$

Expresado en términos de la línea de ancho medio a la mitad del máximo (HWHM) o la línea de ancho FWHM . Calibradas a una altura de pico de la unidad, obtenemos las líneas de Lorentz:${\displaystyle \Delta \nu _{c}/2}$${\displaystyle \Delta \nu _{c}}$

${\displaystyle \gamma _{q,L}(\nu )={\frac {\pi }{2}}\Delta \nu _{c}{\tilde {\gamma }}_{q}(\nu )={\frac {(\Delta \nu _{c}/2)^{2}}{(\Delta \nu _{c}/2)^{2}+(\nu -\nu _{q})^{2}}}={\frac {(\Delta \nu _{c})^{2}}{(\Delta \nu _{c})^{2}+4(\nu -\nu _{q})^{2}}}.}$

Al repetir la transformación de Fourier anterior para todos los modos con índice de modo en el resonador, se obtiene el espectro de modos completo del resonador.${\displaystyle q}$

Dado que el ancho de línea y el rango espectral libre son independientes de la frecuencia, mientras que en el espacio de longitud de onda el ancho de línea no se puede definir adecuadamente y el rango espectral libre depende de la longitud de onda, y dado que las frecuencias de resonancia escalan proporcionalmente a la frecuencia, la respuesta espectral de un resonador Fabry-Pérot se analiza y muestra naturalmente en el espacio de frecuencia.${\displaystyle \Delta \nu _{c}}$${\displaystyle \Delta \nu _{\rm {FSR}}}$${\displaystyle \nu _{q}}$

La respuesta del resonador Fabry-Pérot a un campo eléctrico incidente sobre el espejo 1 se describe mediante varias distribuciones de Airy (nombradas en honor al matemático y astrónomo George Biddell Airy ) que cuantifican la intensidad de la luz en la dirección de propagación hacia adelante o hacia atrás en diferentes posiciones dentro o fuera del resonador con respecto a la intensidad de la luz emitida o incidente. La respuesta del resonador Fabry-Pérot se deriva más fácilmente mediante el uso del enfoque del campo circulante. ^[12] Este enfoque supone un estado estable y relaciona los diversos campos eléctricos entre sí (consulte la figura "Campos eléctricos en un resonador Fabry-Pérot").

El campo puede estar relacionado con el campo que se lanza al resonador por${\displaystyle E_{\rm {circ}}}$${\displaystyle E_{\rm {laun}}}$

${\displaystyle E_{\rm {circ}}=E_{\rm {laun}}+E_{\rm {RT}}=E_{\rm {laun}}+r_{1}r_{2}e^{-i2\phi }E_{\rm {circ}}\Rightarrow {\frac {E_{\rm {circ}}}{E_{\rm {laun}}}}={\frac {1}{1-r_{1}r_{2}e^{-i2\phi }}}.}$

La distribución genérica de Airy, que considera únicamente los procesos físicos exhibidos por la luz dentro del resonador, se deriva entonces como la intensidad que circula en el resonador en relación con la intensidad lanzada, ^[10]

${\displaystyle A_{\rm {circ}}={\frac {I_{\rm {circ}}}{I_{\rm {laun}}}}={\frac {\left|E_{\rm {circ}}\right|^{2}}{\left|E_{\rm {laun}}\right|^{2}}}={\frac {1}{\left|1-r_{1}r_{2}e^{-i2\phi }\right|^{2}}}={\frac {1}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}.}$

${\displaystyle A_{\rm {circ}}}$representa la mejora de resonancia interna dependiente del espectro que proporciona el resonador a la luz que se le lanza (véase la figura "Mejora de resonancia en un resonador Fabry-Pérot"). En las frecuencias de resonancia , donde es igual a cero, el factor de mejora de resonancia interna es${\displaystyle \nu _{q}}$${\displaystyle \sin(\phi )}$

${\displaystyle A_{\rm {circ}}(\nu _{q})={\frac {1}{\left(1-{\sqrt {R_{1}R_{2}}}\right)^{2}}}.}$

Una vez establecida la mejora de resonancia interna, la distribución genérica de Airy, todas las demás distribuciones de Airy se pueden deducir mediante factores de escala simples. ^[10] Dado que la intensidad lanzada al resonador es igual a la fracción transmitida de la intensidad incidente sobre el espejo 1,

${\displaystyle I_{\text{laun}}=\left(1-R_{1}\right)I_{\text{inc}},}$

y las intensidades transmitidas a través del espejo 2, reflejadas en el espejo 2 y transmitidas a través del espejo 1 son las fracciones transmitidas y reflejadas/transmitidas de la intensidad que circula dentro del resonador,

${\displaystyle {\begin{aligned}I_{\text{trans}}&=\left(1-R_{2}\right)I_{\text{circ}},\\I_{\text{b-circ}}&=R_{2}I_{\text{circ}},\\I_{\text{back}}&=\left(1-R_{1}\right)I_{\text{b-circ}},\end{aligned}}}$

respectivamente, las otras distribuciones de Airy con respecto a la intensidad lanzada y con respecto a la intensidad incidente son ^[10]${\displaystyle A}$${\displaystyle I_{\text{laun}}}$${\displaystyle A^{\prime }}$${\displaystyle I_{\text{inc}}}$

${\displaystyle {\begin{aligned}A_{\text{circ}}&={\frac {1}{R_{2}}}A_{\text{b-circ}}={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}={\frac {1}{1-R_{2}}}A_{\text{trans}}={\frac {1}{(1-R_{1})R_{2}}}A_{\text{back}}={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}},\\A_{\text{circ}}'&={\frac {1}{R_{2}}}A_{\text{b-circ}}'={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}'={\frac {1}{1-R_{2}}}A_{\text{trans}}'={\frac {1}{(1-R_{1})R_{2}}}A_{\text{back}}'={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}}',\\A_{\text{circ}}'&=\left(1-R_{1}\right)A_{\text{circ}}.\end{aligned}}}$

El índice "emitir" denota distribuciones de Airy que consideran la suma de intensidades emitidas en ambos lados del resonador.

La intensidad retrotransmitida no se puede medir, ya que la luz retrorreflejada inicial se suma a la señal que se propaga hacia atrás. El caso medible de la intensidad resultante de la interferencia de ambos campos eléctricos que se propagan hacia atrás da como resultado la distribución de Airy ^[10].${\displaystyle I_{\text{back}}}$

${\displaystyle A_{\text{refl}}^{\prime }={\frac {I_{\text{refl}}}{I_{\text{inc}}}}={\frac {\left|E_{\text{refl}}\right|^{2}}{\left|E_{\text{inc}}\right|^{2}}}={\frac {\left({{\sqrt {R_{1}}}-{\sqrt {R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}.}$

Se puede demostrar fácilmente que en un resonador Fabry-Pérot, a pesar de la aparición de interferencias constructivas y destructivas, la energía se conserva en todas las frecuencias:

${\displaystyle A_{\text{trans}}^{\prime }+A_{\text{refl}}^{\prime }={\frac {I_{\text{trans}}+I_{\text{refl}}}{I_{\text{inc}}}}=1.}$

El factor de mejora de la resonancia externa (ver figura "Mejora de la resonancia en un resonador Fabry-Pérot") es ^[10]

${\displaystyle A_{\text{circ}}^{\prime }={\frac {I_{\text{circ}}}{I_{\text{inc}}}}=(1-R_{1})A_{\text{circ}}={\frac {1-R_{1}}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}.}$

En las frecuencias de resonancia , donde es igual a cero, el factor de mejora de resonancia externa es${\displaystyle \nu _{q}}$${\displaystyle \sin(\phi )}$

${\displaystyle A_{\text{circ}}^{\prime }(\nu _{q})={\frac {1-R_{1}}{\left(1-{\sqrt {R_{1}R_{2}}}\right)^{2}}}.}$

Generalmente la luz se transmite a través de un resonador Fabry-Pérot. Por lo tanto, una distribución de Airy que se aplica con frecuencia es ^[10]

${\displaystyle A_{\text{trans}}^{\prime }={\frac {I_{\text{trans}}}{I_{\text{inc}}}}=(1-R_{1})(1-R_{2})A_{\text{circ}}={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}.}$

Describe la fracción de la intensidad de una fuente de luz que incide sobre el espejo 1 y que se transmite a través del espejo 2 (véase la figura "Distribución de Airy "). Su valor pico en las frecuencias de resonancia es${\displaystyle I_{\text{trans}}}$${\displaystyle I_{\text{inc}}}$${\displaystyle A_{\text{trans}}^{\prime }}$${\displaystyle \nu _{q}}$

${\displaystyle A_{\text{trans}}^{\prime }(\nu _{q})={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}}}.}$

El valor pico es igual a la unidad, es decir, toda la luz que incide sobre el resonador se transmite. En consecuencia, no se refleja luz, como resultado de la interferencia destructiva entre los campos y .${\displaystyle R_{1}=R_{2}}$${\displaystyle A_{\text{refl}}^{\prime }=0}$${\displaystyle E_{{\text{refl}},1}}$${\displaystyle E_{\text{back}}}$

${\displaystyle A_{\text{trans}}^{\prime }}$Se ha derivado en el enfoque de campo circulante ^[12] considerando un cambio de fase adicional durante cada transmisión a través de un espejo,${\displaystyle e^{i\pi /2}}$

${\displaystyle {\begin{aligned}E_{\text{circ}}=it_{1}E_{\text{inc}}+r_{1}r_{2}e^{-i2\phi }E_{\text{circ}}&\Rightarrow {\frac {E_{\text{circ}}}{E_{\text{inc}}}}={\frac {it_{1}}{1-r_{1}r_{2}e^{-i2\phi }}},\\E_{\text{trans}}=it_{2}E_{\text{circ}}e^{-i\phi }&\Rightarrow {\frac {E_{\text{trans}}}{E_{\text{inc}}}}={\frac {-t_{1}t_{2}e^{-i\phi }}{1-r_{1}r_{2}e^{-i2\phi }}},\end{aligned}}}$

Resultando en

${\displaystyle A_{\text{trans}}^{\prime }={\frac {I_{\text{trans}}}{I_{\text{inc}}}}={\frac {\left|E_{\text{trans}}\right|^{2}}{\left|E_{\text{inc}}\right|^{2}}}={\frac {\left|-t_{1}t_{2}e^{-i\phi }\right|^{2}}{\left|1-r_{1}r_{2}e^{-i2\phi }\right|^{2}}}={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}.}$

Alternativamente, se puede obtener a través del enfoque de decaimiento de ida y vuelta ^[13] rastreando el número infinito de viajes de ida y vuelta que exhibe el campo eléctrico incidente después de ingresar al resonador y acumulando el campo eléctrico transmitido en todos los viajes de ida y vuelta. El campo transmitido después de la primera propagación y los campos cada vez más pequeños transmitidos después de cada propagación consecutiva a través del resonador son${\displaystyle A_{\text{trans}}^{\prime }}$${\displaystyle E_{\text{inc}}}$${\displaystyle E_{\text{trans}}}$

${\displaystyle {\begin{aligned}E_{\text{trans,1}}&=E_{\text{inc}}it_{1}it_{2}e^{-i\phi }=-E_{\text{inc}}t_{1}t_{2}e^{-i\phi },\\E_{{\text{trans}},m+1}&=E_{{\text{trans}},m}r_{1}r_{2}e^{-i2\phi },\end{aligned}}}$

respectivamente. Explotando

${\displaystyle \sum _{m=0}^{\infty }x^{m}={\frac {1}{1-x}}\Rightarrow E_{\text{trans}}=\sum _{m=1}^{\infty }E_{{\text{trans}},m}=E_{\text{inc}}{\frac {-t_{1}t_{2}e^{-i\phi }}{1-r_{1}r_{2}e^{-i2\phi }}}}$

El resultado es el mismo que el anterior, por lo tanto, se deriva la misma distribución de Airy . Sin embargo, este enfoque es físicamente engañoso, porque supone que la interferencia se produce entre los haces desacoplados después del espejo 2, fuera del resonador, en lugar de los haces lanzados y circulantes después del espejo 1, dentro del resonador. Dado que es la interferencia la que modifica los contenidos espectrales, la distribución de intensidad espectral dentro del resonador sería la misma que la distribución de intensidad espectral incidente, y no se produciría ninguna mejora de resonancia dentro del resonador.${\displaystyle E_{\text{trans}}/E_{\text{inc}}}$${\displaystyle A_{\text{trans}}^{\prime }}$

Físicamente, la distribución de Airy es la suma de los perfiles de modo de los modos del resonador longitudinal. ^[10] A partir del campo eléctrico que circula dentro del resonador, se considera la descomposición exponencial en el tiempo de este campo a través de ambos espejos del resonador, Fourier lo transforma a espacio de frecuencia para obtener las formas de línea espectral normalizadas , lo divide por el tiempo de ida y vuelta para tener en cuenta cómo la intensidad total del campo eléctrico circulante se distribuye longitudinalmente en el resonador y se acopla por unidad de tiempo, lo que da como resultado los perfiles de modo emitidos,${\displaystyle E_{circ}}$${\displaystyle {\tilde {\gamma }}_{q}(\nu )}$${\displaystyle t_{\rm {RT}}}$

${\displaystyle \gamma _{q,{\rm {emit}}}(\nu )={\frac {1}{t_{\rm {RT}}}}{\tilde {\gamma }}_{q}(\nu ),}$

y luego suma los perfiles de modo emitidos de todos los modos longitudinales ^[10]

${\displaystyle \sum _{q=-\infty }^{\infty }\gamma _{q,{\rm {emit}}}(\nu )={\frac {1-R_{1}R_{2}}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}=A_{\rm {emit}},}$

por lo que se iguala la distribución de Airy .${\displaystyle A_{\rm {emit}}}$

Los mismos factores de escala simples que proporcionan las relaciones entre las distribuciones de Airy individuales también proporcionan las relaciones entre y los otros perfiles de modo: ^[10]${\displaystyle \gamma _{q,{\rm {emit}}}(\nu )}$

${\displaystyle \gamma _{q,{\rm {circ}}}={\frac {1}{R_{2}}}\gamma _{q,{\text{b-circ}}}={\frac {1}{R_{1}R_{2}}}\gamma _{q,{\rm {RT}}}={\frac {1}{1-R_{2}}}\gamma _{q,{\rm {trans}}}={\frac {1}{(1-R_{1})R_{2}}}\gamma _{q,{\rm {back}}}={\frac {1}{1-R_{1}R_{2}}}\gamma _{q,{\rm {emit}}},}$

${\displaystyle \gamma _{q,{\rm {circ}}}^{\prime }={\frac {1}{R_{2}}}\gamma _{q,{\text{b-circ}}}^{\prime }={\frac {1}{R_{1}R_{2}}}\gamma _{q,{\rm {RT}}}^{\prime }={\frac {1}{1-R_{2}}}\gamma _{q,{\rm {trans}}}^{\prime }={\frac {1}{(1-R_{1})R_{2}}}\gamma _{q,{\rm {back}}}^{\prime }={\frac {1}{1-R_{1}R_{2}}}\gamma _{q,{\rm {emit}}}^{\prime },}$

${\displaystyle \gamma _{q,{\rm {circ}}}^{\prime }=(1-R_{1})\gamma _{q,{\rm {circ}}}.}$

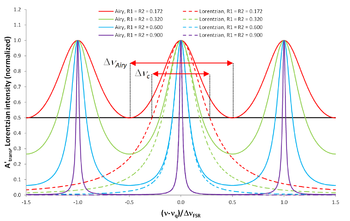
El criterio de Taylor de resolución espectral propone que dos líneas espectrales pueden resolverse si las líneas individuales se cruzan a la mitad de la intensidad. Al introducir luz en el resonador Fabry-Pérot, midiendo la distribución de Airy, se puede derivar la pérdida total del resonador Fabry-Pérot mediante el recálculo del ancho de línea de Lorentz , que se muestra (línea azul) en relación con el rango espectral libre en la figura "Ancho de línea y fineza de Lorentz versus ancho de línea y fineza de Airy de un resonador Fabry-Pérot".${\displaystyle \Delta \nu _{c}}$

Las líneas lorentzianas subyacentes pueden resolverse siempre que se respete el criterio de Taylor (véase la figura "El significado físico de la fineza lorentziana"). En consecuencia, se puede definir la fineza lorentziana de un resonador Fabry-Pérot: ^[10]

${\displaystyle {\mathcal {F}}_{c}={\frac {\Delta \nu _{\rm {FSR}}}{\Delta \nu _{c}}}={\frac {2\pi }{-\ln(R_{1}R_{2})}}.}$

Se muestra como la línea azul en la figura "El significado físico de la fineza de Lorentz". La fineza de Lorentz tiene un significado físico fundamental: describe qué tan bien se pueden resolver las líneas de Lorentz que subyacen a la distribución de Airy al medir la distribución de Airy. En el punto donde${\displaystyle {\mathcal {F}}_{c}}$

${\displaystyle \Delta \nu _{c}=\Delta \nu _{\rm {FSR}}\Rightarrow R_{1}R_{2}=e^{-2\pi }\approx 0.001867,}$

equivalente a , se alcanza el criterio de Taylor para la resolución espectral de una única distribución de Airy. En este punto, , no se pueden distinguir dos líneas espectrales. Para reflectividades especulares iguales, este punto se produce cuando . Por lo tanto, el ancho de línea de las líneas de Lorentz subyacentes a la distribución de Airy de un resonador de Fabry-Pérot se puede resolver midiendo la distribución de Airy, por lo tanto, sus pérdidas de resonador se pueden determinar espectroscópicamente, hasta este punto.${\displaystyle {\mathcal {F}}_{c}=1}$${\displaystyle {\mathcal {F}}_{c}<1}$${\displaystyle R_{1}=R_{2}\approx 4.32\%}$

Cuando el resonador Fabry-Pérot se utiliza como interferómetro de barrido, es decir, con una longitud de resonador variable (o ángulo de incidencia), se pueden distinguir espectroscópicamente líneas espectrales a diferentes frecuencias dentro de un rango espectral libre. Se deben resolver varias distribuciones de Airy, cada una creada por una línea espectral individual. Por lo tanto, la distribución de Airy se convierte en la función fundamental subyacente y la medición proporciona una suma de distribuciones de Airy. Los parámetros que cuantifican adecuadamente esta situación son el ancho de línea de Airy y la fineza de Airy . El ancho de línea FWHM de la distribución de Airy es ^[10]${\displaystyle A_{\rm {trans}}^{\prime }(\nu )}$${\displaystyle \Delta \nu _{\rm {Airy}}}$${\displaystyle {\mathcal {F}}_{\rm {Airy}}}$${\displaystyle \Delta \nu _{\rm {Airy}}}$${\displaystyle A_{\rm {trans}}^{\prime }(\nu )}$

${\displaystyle \Delta \nu _{\rm {Airy}}=\Delta \nu _{\rm {FSR}}{\frac {2}{\pi }}\arcsin \left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right).}$

El ancho de línea de Airy se muestra como una curva verde en la figura "Ancho de línea y fineza de Lorentz versus ancho de línea y fineza de Airy de un resonador Fabry-Pérot".${\displaystyle \Delta \nu _{\rm {Airy}}}$

El concepto de definir el ancho de línea de los picos de Airy como FWHM se rompe en (línea roja continua en la figura "Distribución de Airy "), porque en este punto el ancho de línea de Airy salta instantáneamente a un valor infinito para la función. Para valores de reflectividad más bajos de , el ancho de línea FWHM de los picos de Airy no está definido. El caso límite ocurre en${\displaystyle \Delta \nu _{\rm {Airy}}=\Delta \nu _{\rm {FSR}}}$${\displaystyle A_{\rm {trans}}^{\prime }}$${\displaystyle \arcsin }$${\displaystyle R_{1}R_{2}}$

${\displaystyle \Delta \nu _{\rm {Airy}}=\Delta \nu _{\rm {FSR}}\Rightarrow {\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}=1\Rightarrow R_{1}R_{2}\approx 0.02944.}$

Para reflectividades de espejo iguales, este punto se alcanza cuando (línea roja continua en la figura "Distribución de Airy ").${\displaystyle R_{1}=R_{2}\approx 17.2\%}$${\displaystyle A_{\rm {trans}}^{\prime }}$

La finura de la distribución de Airy de un resonador Fabry-Pérot, que se muestra como la curva verde en la figura "Ancho de línea y finura de Lorentz versus ancho de línea y finura de Airy de un resonador Fabry-Pérot" en comparación directa con la finura de Lorentz , se define como ^[10]${\displaystyle {\mathcal {F}}_{c}}$

${\displaystyle {\mathcal {F}}_{\rm {Airy}}={\frac {\Delta \nu _{\rm {FSR}}}{\Delta \nu _{\rm {Airy}}}}={\frac {\pi }{2}}\left[\arcsin \left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right)\right]^{-1}.}$

Al escanear la longitud del resonador Fabry-Pérot (o el ángulo de la luz incidente), la fineza de Airy cuantifica el número máximo de distribuciones de Airy creadas por la luz en frecuencias individuales dentro del rango espectral libre del resonador Fabry-Pérot, cuyos picos adyacentes se pueden distinguir inequívocamente espectroscópicamente, es decir, no se superponen en su FWHM (ver figura "El significado físico de la fineza de Airy"). Esta definición de la fineza de Airy es consistente con el criterio de Taylor de la resolución de un espectrómetro. Dado que el concepto de ancho de línea FWHM se rompe en , en consecuencia, la fineza de Airy se define solo hasta , ver la figura "Ancho de línea y fineza de Lorentz versus ancho de línea y fineza de Airy de un resonador Fabry-Pérot".${\displaystyle \nu _{m}}$${\displaystyle \Delta \nu _{\rm {Airy}}=\Delta \nu _{\rm {FSR}}}$${\displaystyle {\mathcal {F}}_{\rm {Airy}}=1}$

A menudo se realiza una aproximación innecesaria al derivar del ancho de línea de Airy . A diferencia de la solución exacta anterior, conduce a${\displaystyle \sin {(\phi )}\approx \phi }$${\displaystyle A_{\rm {trans}}^{\prime }}$${\displaystyle \Delta \nu _{\rm {Airy}}}$

${\displaystyle \Delta \nu _{\rm {Airy}}\approx \Delta \nu _{\rm {FSR}}{\frac {1}{\pi }}{\frac {1-{\sqrt {R_{1}R_{2}}}}{\sqrt[{4}]{R_{1}R_{2}}}}\Rightarrow {\mathcal {F}}_{\rm {Airy}}={\frac {\Delta \nu _{\rm {FSR}}}{\Delta \nu _{\rm {Airy}}}}\approx \pi {\frac {\sqrt[{4}]{R_{1}R_{2}}}{1-{\sqrt {R_{1}R_{2}}}}}.}$

Esta aproximación del ancho de línea de Airy, que se muestra como la curva roja en la figura "Ancho de línea y fineza de Lorentz versus ancho de línea y fineza de Airy de un resonador Fabry-Pérot", se desvía de la curva correcta en reflectividades bajas y no se descompone incorrectamente cuando . Esta aproximación se suele utilizar también para calcular la fineza de Airy.${\displaystyle \Delta \nu _{\rm {Airy}}>\Delta \nu _{\rm {FSR}}}$

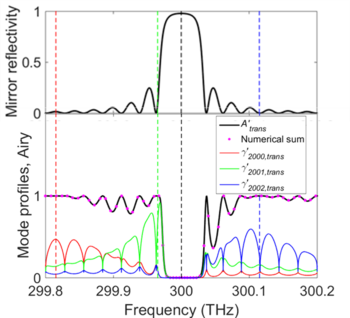
El caso más general de un resonador Fabry-Pérot con reflectividades de espejo dependientes de la frecuencia se puede tratar con las mismas ecuaciones que antes, excepto que el tiempo de decaimiento del fotón y el ancho de línea ahora se convierten en funciones locales de la frecuencia. Mientras que el tiempo de decaimiento del fotón sigue siendo una cantidad bien definida, el ancho de línea pierde su significado, porque se asemeja a un ancho de banda espectral, cuyo valor ahora cambia dentro de ese mismo ancho de banda. También en este caso, cada distribución de Airy es la suma de todos los perfiles de modos subyacentes que pueden distorsionarse fuertemente. ^[10] Un ejemplo de la distribución de Airy y algunos de los perfiles de modos subyacentes se da en la figura "Ejemplo de un resonador Fabry-Pérot con reflectividad de espejo dependiente de la frecuencia".${\displaystyle \tau _{c}(\nu )}$${\displaystyle \Delta \nu _{c}(\nu )}$${\displaystyle A_{\rm {trans}}^{\prime }}$${\displaystyle \gamma _{q,{\rm {trans}}}^{\prime }(\nu )}$

Las pérdidas de propagación intrínsecas dentro del resonador se pueden cuantificar mediante un coeficiente de pérdida de intensidad por unidad de longitud o, equivalentemente, mediante la pérdida de ida y vuelta intrínseca tal que ^[14]${\displaystyle \alpha _{\rm {loss}}}$${\displaystyle L_{\rm {RT}},}$

${\displaystyle 1-L_{\rm {RT}}=e^{-\alpha _{\rm {loss}}2\ell }=e^{-t_{\rm {RT}}/\tau _{\rm {loss}}}.}$

La pérdida adicional acorta el tiempo de desintegración de fotones del resonador: ^[14]${\displaystyle \tau _{c}}$

${\displaystyle {\frac {1}{\tau _{c}}}={\frac {1}{\tau _{\rm {out}}}}+{\frac {1}{\tau _{\rm {loss}}}}={\frac {-\ln {[R_{1}R_{2}(1-L_{\rm {RT}})]}}{t_{\rm {RT}}}}={\frac {-\ln {[R_{1}R_{2}]}}{t_{\rm {RT}}}}+c\alpha _{\rm {loss}}.}$

donde es la velocidad de la luz en la cavidad. La distribución genérica de Airy o factor de mejora de resonancia interna se deriva entonces como se indicó anteriormente incluyendo las pérdidas de propagación a través del coeficiente de pérdida de amplitud : ^[14]${\displaystyle c}$${\displaystyle A_{\rm {circ}}}$${\displaystyle \alpha _{\rm {loss}}/2}$

${\displaystyle E_{\rm {circ}}=E_{\rm {laun}}+E_{\rm {RT}}=E_{\rm {laun}}+r_{1}r_{2}e^{-(\alpha _{\rm {loss}}/2)2\ell }e^{-i2\phi }E_{\rm {circ}}\Rightarrow {\frac {E_{\rm {circ}}}{E_{\rm {laun}}}}={\frac {1}{1-r_{1}r_{2}e^{-\alpha _{\rm {loss}}\ell }e^{-i2\phi }}}\Rightarrow }$

${\displaystyle A_{\rm {circ}}={\frac {I_{\rm {circ}}}{I_{\rm {laun}}}}={\frac {\left|E_{\rm {circ}}\right|^{2}}{\left|E_{\rm {laun}}\right|^{2}}}={\frac {1}{\left|1-r_{1}r_{2}e^{-\alpha _{\rm {loss}}\ell }e^{-i2\phi }\right|^{2}}}={\frac {1}{\left({1-{\sqrt {R_{1}R_{2}}}e^{-\alpha _{\rm {loss}}\ell }}\right)^{2}+4{\sqrt {R_{1}R_{2}}}e^{-\alpha _{\rm {loss}}\ell }\sin ^{2}(\phi )}}.}$

Las demás distribuciones de Airy se pueden derivar como se indicó anteriormente, teniendo en cuenta además las pérdidas de propagación. En particular, la función de transferencia con pérdida se convierte en ^[14]

${\displaystyle A_{\text{trans}}^{\prime }={\frac {I_{\rm {trans}}}{I_{\rm {inc}}}}=(1-R_{1})(1-R_{2})e^{-\alpha _{\rm {loss}}\ell }A_{\rm {circ}}={\frac {(1-R_{1})(1-R_{2})e^{-\alpha _{\rm {loss}}\ell }}{\left({1-{\sqrt {R_{1}R_{2}}}e^{-\alpha _{\rm {loss}}\ell }}\right)^{2}+4{\sqrt {R_{1}R_{2}}}e^{-\alpha _{\rm {loss}}\ell }\sin ^{2}(\phi )}}.}$

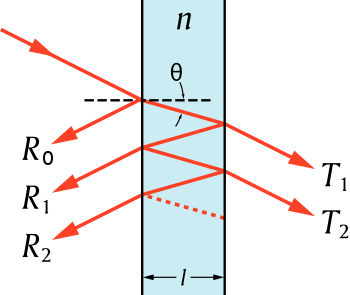
La función de transmisión variable de un etalón se debe a la interferencia entre las múltiples reflexiones de luz entre las dos superficies reflectantes. La interferencia constructiva se produce si los rayos transmitidos están en fase , y esto corresponde a un pico de alta transmisión del etalón. Si los rayos transmitidos están desfasados, se produce una interferencia destructiva, y esto corresponde a un mínimo de transmisión. El que los rayos reflejados múltiples estén en fase o no depende de la longitud de onda (λ) de la luz (en el vacío), el ángulo en el que la luz viaja a través del etalón (θ), el espesor del etalón ( ℓ ) y el índice de refracción del material entre las superficies reflectantes ( n ).

La diferencia de fase entre cada par transmitido sucesivo (es decir, T ₂ y T ₁ en el diagrama) se da por ^[15]

${\displaystyle \delta =\left({\frac {2\pi }{\lambda }}\right)2n\ell \cos \theta .}$

Si ambas superficies tienen una reflectancia R , la función de transmitancia del etalón viene dada por

${\displaystyle T_{e}={\frac {(1-R)^{2}}{1-2R\cos \delta +R^{2}}}={\frac {1}{1+F\sin ^{2}\left({\frac {\delta }{2}}\right)}},}$

dónde

${\displaystyle F={\frac {4R}{(1-R)^{2}}}}$

es el coeficiente de finura .

La transmisión máxima ( ) ocurre cuando la diferencia de longitud del camino óptico ( ) entre cada haz transmitido es un múltiplo entero de la longitud de onda. En ausencia de absorción, la reflectancia del etalón R _e es el complemento de la transmitancia, de modo que . La reflectividad máxima está dada por${\displaystyle T_{e}=1}$${\displaystyle 2nl\cos \theta }$${\displaystyle T_{e}+R_{e}=1}$

${\displaystyle R_{\max }=1-{\frac {1}{1+F}}={\frac {4R}{(1+R)^{2}}},}$

y esto ocurre cuando la diferencia de longitud de trayectoria es igual a la mitad de un múltiplo impar de la longitud de onda.

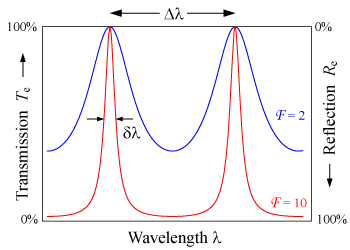
La separación de longitud de onda entre picos de transmisión adyacentes se denomina rango espectral libre (FSR) del etalón, Δλ, y viene dada por:

${\displaystyle \Delta \lambda ={\frac {\lambda _{0}^{2}}{2n_{\mathrm {g} }\ell \cos \theta +\lambda _{0}}}\approx {\frac {\lambda _{0}^{2}}{2n_{\mathrm {g} }\ell \cos \theta }},}$

donde λ ₀ es la longitud de onda central del pico de transmisión más cercano y es el índice de refracción del grupo . ^[16] El FSR está relacionado con el semimáximo de ancho completo, δλ, de cualquier banda de transmisión por una cantidad conocida como finesse :${\displaystyle n_{\mathrm {g} }}$

${\displaystyle {\mathcal {F}}={\frac {\Delta \lambda }{\delta \lambda }}={\frac {\pi }{2\arcsin \left({\frac {1}{\sqrt {F}}}\right)}}.}$

Esto se aproxima comúnmente (para R  > 0,5) mediante

${\displaystyle {\mathcal {F}}\approx {\frac {\pi {\sqrt {F}}}{2}}={\frac {\pi R^{\frac {1}{2}}}{1-R}}.}$

Si los dos espejos no son iguales, la finura se convierte en

${\displaystyle {\mathcal {F}}\approx {\frac {\pi \left(R_{1}R_{2}\right)^{\frac {1}{4}}}{1-\left(R_{1}R_{2}\right)^{\frac {1}{2}}}}.}$

Los etalones con alta fineza muestran picos de transmisión más agudos con coeficientes de transmisión mínimos más bajos. En el caso de incidencia oblicua, la fineza dependerá del estado de polarización del haz, ya que el valor de R , dado por las ecuaciones de Fresnel , es generalmente diferente para polarizaciones p y s .

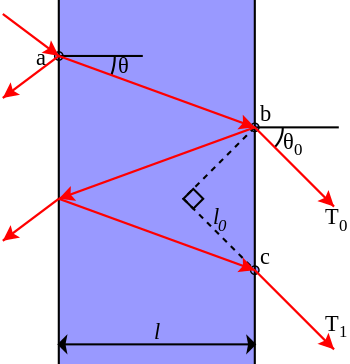
En el diagrama de la derecha se muestran dos haces, uno de los cuales (T ₀ ) se transmite a través del etalón y el otro (T ₁ ) se refleja dos veces antes de transmitirse. En cada reflexión, la amplitud se reduce en , mientras que en cada transmisión a través de una interfaz la amplitud se reduce en . Suponiendo que no hay absorción, la conservación de la energía requiere T  +  R  = 1. En la derivación siguiente, n es el índice de refracción dentro del etalón y n ₀ es el exterior del etalón. Se supone que n > n ₀ . La amplitud incidente en el punto a se toma como uno y se utilizan fasores para representar la amplitud de la radiación. La amplitud transmitida en el punto b será entonces${\displaystyle {\sqrt {R}}}$${\displaystyle {\sqrt {T}}}$

${\displaystyle t_{0}=T\,e^{ik\ell /\cos \theta },}$

donde es el número de onda dentro del etalón y λ es la longitud de onda del vacío. En el punto c la amplitud transmitida será${\displaystyle k=2\pi n/\lambda }$

${\displaystyle t'_{1}=TR\,e^{3ik\ell /\cos \theta }.}$

La amplitud total de ambos haces será la suma de las amplitudes de los dos haces medidas a lo largo de una línea perpendicular a la dirección del haz. Por lo tanto, la amplitud t ₀ en el punto b se puede sumar a t ' ₁ retardada en fase por una cantidad , donde es el número de onda fuera del etalón. Por lo tanto,${\displaystyle k_{0}\ell _{0}}$${\displaystyle k_{0}=2\pi n_{0}/\lambda }$

${\displaystyle t_{1}=TR\,e^{\left(3ik\ell /\cos \theta \right)-ik_{0}\ell _{0}},}$

donde ℓ ₀ es

${\displaystyle \ell _{0}=2\ell \tan \theta \sin \theta _{0}.}$

La diferencia de fase entre los dos haces es

${\displaystyle \delta ={2k\ell \over \cos \theta }-k_{0}\ell _{0}.}$

La relación entre θ y θ ₀ viene dada por la ley de Snell :

${\displaystyle n\sin \theta =n_{0}\sin \theta _{0},}$

de modo que la diferencia de fase puede escribirse como

${\displaystyle \delta =2k\ell \,\cos \theta .}$

Dentro de un factor de fase multiplicativo constante, la amplitud del haz transmitido m se puede escribir como

${\displaystyle t_{m}=TR^{m}e^{im\delta }.}$

La amplitud total transmitida es la suma de las amplitudes de todos los haces individuales:

${\displaystyle t=\sum _{m=0}^{\infty }t_{m}=T\sum _{m=0}^{\infty }R^{m}\,e^{im\delta }.}$

La serie es una serie geométrica , cuya suma puede expresarse analíticamente. La amplitud puede reescribirse como

${\displaystyle t={\frac {T}{1-Re^{i\delta }}}.}$

La intensidad del haz será exactamente t veces su conjugado complejo . Como se supuso que el haz incidente tenía una intensidad de uno, esto también dará la función de transmisión:

${\displaystyle T_{e}=tt^{*}={\frac {T^{2}}{1+R^{2}-2R\cos \delta }}.}$

Para una cavidad asimétrica, es decir, una con dos espejos diferentes, la forma general de la función de transmisión es

${\displaystyle T_{e}={\frac {T_{1}T_{2}}{1+R_{1}R_{2}-2{\sqrt {R_{1}R_{2}}}\cos \delta }}.}$

Un interferómetro Fabry-Pérot se diferencia de un etalón Fabry-Pérot en que la distancia ℓ entre las placas se puede ajustar para cambiar las longitudes de onda en las que se producen los picos de transmisión en el interferómetro. Debido a la dependencia del ángulo de la transmisión, los picos también se pueden desplazar girando el etalón con respecto al haz.

Otra expresión para la función de transmisión ya se derivó en la descripción en el espacio de frecuencia como la suma infinita de todos los perfiles de modos longitudinales. La definición de la expresión anterior se puede escribir como${\displaystyle \gamma =\ln \left({\frac {1}{R}}\right)}$

${\displaystyle T_{e}={\frac {T^{2}}{1-R^{2}}}\left({\frac {\sinh \gamma }{\cosh \gamma -\cos \delta }}\right).}$

El segundo término es proporcional a una distribución lorentziana envuelta, de modo que la función de transmisión puede escribirse como una serie de funciones lorentzianas :

${\displaystyle T_{e}={\frac {2\pi \,T^{2}}{1-R^{2}}}\,\sum _{\ell =-\infty }^{\infty }L(\delta -2\pi \ell ;\gamma ),}$

dónde

${\displaystyle L(x;\gamma )={\frac {\gamma }{\pi \left(x^{2}+\gamma ^{2}\right)}}.}$

• Interferómetro de Lummer-Gehrcke
• Étalón de Gires-Tournois
• Filtro de línea atómico
• Guía de ondas ARROW
• Reflector Bragg distribuido
• Rejilla de Bragg de fibra
• Microcavidad óptica
• Interferencia de película delgada
• Ancho de línea del láser

• Hernández, G. (1986). Interferómetros Fabry-Perot . Cambridge: Cambridge University Press . ISBN. 0-521-32238-3.

• Diseño avanzado de etalones por Precision Photonics Corporation