Paralaje estelar

La paralaje estelar es el cambio aparente de posición ( paralaje ) de cualquier estrella cercana (u otro objeto) con respecto al fondo de estrellas distantes. Por extensión, es un método para determinar la distancia a la estrella a través de la trigonometría, el método de paralaje estelar . Creado por las diferentes posiciones orbitales de la Tierra , el cambio observado extremadamente pequeño es mayor en intervalos de tiempo de aproximadamente seis meses, cuando la Tierra llega a lados opuestos del Sol en su órbita, dando una distancia de referencia de aproximadamente dos unidades astronómicas entre observaciones. Se considera que el paralaje en sí es la mitad de este máximo, aproximadamente equivalente al cambio de observación que se produciría debido a las diferentes posiciones de la Tierra y el Sol, una línea de base de una unidad astronómica (UA).

La paralaje estelar es tan difícil de detectar que su existencia fue objeto de mucho debate en astronomía durante cientos de años. Thomas Henderson , Friedrich Georg Wilhelm von Struve y Friedrich Bessel realizaron las primeras mediciones exitosas de paralaje en 1832-1838, para las estrellas Alpha Centauri , Vega y 61 Cygni .

La paralaje estelar es tan pequeña que no se pudo observar hasta el siglo XIX, y su aparente ausencia se utilizó como argumento científico contra el heliocentrismo durante la temprana edad moderna . De la geometría de Euclides se desprende claramente que el efecto sería indetectable si las estrellas estuvieran lo suficientemente lejos, pero por diversas razones, distancias tan gigantescas parecían completamente improbables: una de las principales objeciones de Tycho Brahe al heliocentrismo copernicano era que para que fuera compatible con la falta de paralaje estelar observable, tendría que haber un enorme e improbable vacío entre la órbita de Saturno y la octava esfera (las estrellas fijas). ^[1]

James Bradley intentó por primera vez medir las paralajes estelares en 1729. El movimiento estelar resultó demasiado insignificante para su telescopio , pero en su lugar descubrió la aberración de la luz ^[2] y la nutación del eje de la Tierra, y catalogó 3.222 estrellas.

La medición de la paralaje anual fue la primera forma fiable de determinar las distancias a las estrellas más cercanas. En el segundo cuarto del siglo XIX, el progreso tecnológico alcanzó un nivel que proporcionó suficiente exactitud y precisión para las mediciones de paralaje estelar. Giuseppe Calandrelli observó el paralaje estelar en 1805-6 y llegó a un valor de 4 segundos para la estrella Vega que era una sobreestimación enorme. ^[3] Las primeras mediciones exitosas de paralaje estelar fueron realizadas por Thomas Henderson en Ciudad del Cabo , Sudáfrica, en 1832-1833, donde midió el paralaje de una de las estrellas más cercanas, Alpha Centauri . ^{[4] [5]} Entre 1835 y 1836, el astrónomo Friedrich Georg Wilhelm von Struve en el observatorio de la universidad de Dorpat midió la distancia de Vega , publicando sus resultados en 1837. ^[6] Friedrich Bessel , un amigo de Struve, llevó a cabo una intensa campaña de observación en 1837-1838 en el Observatorio de Koenigsberg para la estrella 61 Cygni usando un heliómetro , y publicó sus resultados en 1838. ^{[7] [8]} Henderson publicó sus resultados en 1839, después de regresar de Sudáfrica.

Estos tres resultados, dos de los cuales fueron medidos con los mejores instrumentos de la época (el gran refractor Fraunhofer utilizado por Struve y el heliómetro Fraunhofer de Bessel), fueron los primeros en la historia en establecer la escala fiable de distancias a las estrellas. ^[9]

En 1896 se instaló un gran heliómetro en el Observatorio Kuffner (Viena) y se utilizó para medir la distancia a otras estrellas mediante paralaje trigonométrico. ^[10] En 1910, había calculado 16 distancias de paralaje a otras estrellas, de un total de solo 108 conocidas por la ciencia en ese momento. ^[10]

Al ser muy difícil de medir, a finales del siglo XIX sólo se habían obtenido unas 60 paralajes estelares, en su mayoría mediante el uso del micrómetro filar . Los astrógrafos que utilizaban placas fotográficas astronómicas aceleraron el proceso a principios del siglo XX. Las máquinas de medición de placas automatizadas ^[11] y la tecnología informática más sofisticada de la década de 1960 permitieron una compilación más eficiente de catálogos de estrellas . En la década de 1980, los dispositivos acoplados a carga (CCD) sustituyeron a las placas fotográficas y redujeron las incertidumbres ópticas a un milisegundo de arco. ^{[ cita requerida ]}

La paralaje estelar sigue siendo el estándar para calibrar otros métodos de medición (véase Escala de distancias cósmicas ). Los cálculos precisos de la distancia basados ​​en la paralaje estelar requieren una medición de la distancia entre la Tierra y el Sol, que ahora se conoce con una precisión exquisita basada en la reflexión del radar en las superficies de los planetas. ^[12]

En 1989 se lanzó el satélite Hipparcos , cuyo principal objetivo era obtener paralajes y movimientos propios de estrellas cercanas, aumentando mil veces el número de paralajes estelares medidos con una precisión de milisegundos de arco. Aun así, Hipparcos solo puede medir ángulos de paralaje de estrellas situadas hasta unos 1.600 años luz de distancia, un poco más del uno por ciento del diámetro de la Vía Láctea .

El telescopio Hubble WFC3 tiene ahora una precisión de 20 a 40 microsegundos de arco, lo que permite realizar mediciones de distancias fiables de hasta 3.066 parsecs (10.000 años luz) para un pequeño número de estrellas. ^[14] Esto da más precisión a la escala de distancias cósmicas y mejora el conocimiento de las distancias en el Universo, basándose en las dimensiones de la órbita de la Tierra.

A medida que aumentan las distancias entre los dos puntos de observación, el efecto visual del paralaje también se hace más visible. La sonda espacial New Horizons de la NASA realizó la primera medición de paralaje interestelar el 22 de abril de 2020, tomando imágenes de Proxima Centauri y Wolf 359 en conjunto con observatorios terrestres. La proximidad relativa de las dos estrellas combinada con la distancia de 6.500 millones de kilómetros (aproximadamente 43 UA) de la sonda a la Tierra produjo un paralaje discernible de minutos de arco, lo que permitió ver el paralaje visualmente sin instrumentación. ^[15]

Se espera que la misión Gaia de la Agencia Espacial Europea , lanzada el 19 de diciembre de 2013, mida los ángulos de paralaje con una precisión de 10 microsegundos de arco para todas las estrellas moderadamente brillantes, cartografiando así las estrellas cercanas (y potencialmente los planetas) hasta una distancia de decenas de miles de años luz de la Tierra. ^[17] La ​​publicación de datos 2 de 2018 afirma que los errores medios para los paralajes de magnitud 15 y estrellas más brillantes son de 20 a 40 microsegundos de arco. ^[18]

La interferometría de línea de base muy larga en la banda de radio puede producir imágenes con resoluciones angulares de aproximadamente 1 milisegundo de arco y, por lo tanto, para fuentes de radio brillantes, la precisión de las mediciones de paralaje realizadas en la radio puede superar fácilmente ^{[ dudoso – discutir ]} las de los telescopios ópticos como Gaia. Estas mediciones tienden a tener una sensibilidad limitada y deben realizarse una a la vez, por lo que el trabajo generalmente se realiza solo para fuentes como púlsares y sistemas binarios de rayos X, donde la emisión de radio es fuerte en relación con la emisión óptica. ^{[ cita requerida ]}

Esta sección necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables en esta sección. El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Paralaje estelar» – noticias  · periódicos  · libros  · académico  · JSTOR ( junio de 2020 ) ( Aprenda cómo y cuándo eliminar este mensaje )

A lo largo del año se anota la posición de una estrella S en relación con otras estrellas en su vecindad aparente:

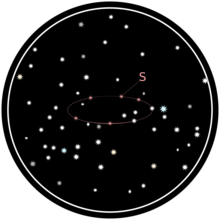
Las estrellas que no parecen moverse entre sí se utilizan como puntos de referencia para determinar la trayectoria de S.

La trayectoria observada es una elipse: la proyección de la órbita de la Tierra alrededor del Sol a través de S sobre el fondo distante de estrellas inmóviles. Cuanto más se aleja S del eje orbital de la Tierra, mayor es la excentricidad de la trayectoria de S. El centro de la elipse corresponde al punto en el que S se vería desde el Sol:

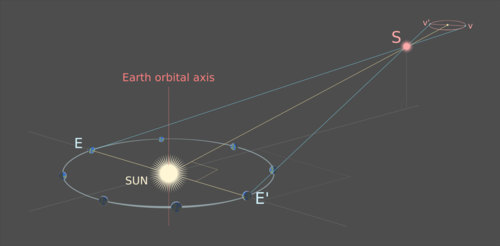
El plano de la órbita de la Tierra forma un ángulo con una línea que va del Sol a través de S. Los vértices v y v' de la proyección elíptica de la trayectoria de S son proyecciones de las posiciones de la Tierra E y E ′ tales que una línea EE ′ interseca la línea Sol-S en un ángulo recto; el triángulo creado por los puntos E, E ′ y S es un triángulo isósceles con la línea Sol-S como su eje de simetría.

Las estrellas que no se han movido entre las observaciones están, a efectos de la precisión de la medición, infinitamente lejanas. Esto significa que la distancia del movimiento de la Tierra en comparación con la distancia a estas estrellas infinitamente lejanas es, dentro de la precisión de la medición, 0. Por lo tanto, una línea de visión desde la primera posición de la Tierra E hasta el vértice v será esencialmente la misma que una línea de visión desde la segunda posición de la Tierra E ′ hasta el mismo vértice v y, por lo tanto, correrá paralela a ella, lo que es imposible de representar de manera convincente en una imagen de tamaño limitado:

Como la línea E ′ -v ′ es una transversal en el mismo plano (aproximadamente euclidiano) que las líneas paralelas Ev y E ′ -v, se deduce que los ángulos correspondientes de intersección de estas líneas paralelas con esta transversal son congruentes: el ángulo θ entre las líneas de visión Ev y E ′ -v ′ es igual al ángulo θ entre E ′ -v y E ′ -v ′ , que es el ángulo θ entre las posiciones observadas de S en relación con su entorno estelar aparentemente inmóvil.

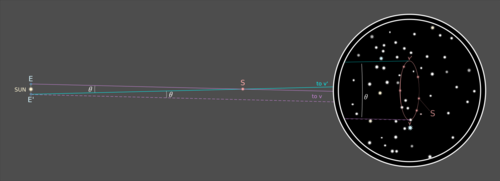
La distancia d del Sol a S se deduce ahora de una simple trigonometría:

 bronceado (1/2⁠ θ) = E-Sol / d,

de modo que d = E-Sol / tan( ⁠1/2⁠ θ), donde E-Sol es 1 UA.

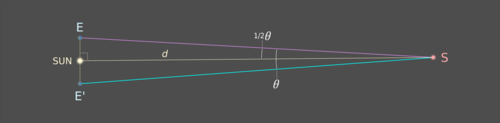
Cuanto más distante esté un objeto, menor será su paralaje.

Las medidas de paralaje estelar se dan en las minúsculas unidades de segundos de arco , o incluso en milésimas de segundos de arco (milisegundos de arco). La unidad de distancia parsec se define como la longitud del cateto de un triángulo rectángulo adyacente al ángulo de un segundo de arco en un vértice , donde el otro cateto tiene una longitud de 1 UA. Debido a que los paralajes estelares y las distancias implican todos estos delgados triángulos rectángulos , se puede utilizar una aproximación trigonométrica conveniente para convertir paralajes (en segundos de arco) a distancia (en parsecs). La distancia aproximada es simplemente el recíproco del paralaje: por ejemplo, Proxima Centauri (la estrella más cercana a la Tierra aparte del Sol), cuyo paralaje es 0,7685, está a 1 / 0,7685 parsecs = 1,301 parsecs (4,24 años luz) de distancia. ^[19]${\displaystyle d{\text{ (pc)}}\approx 1/p{\text{ (arcosegundo)}}.}$

La paralaje estelar se mide con mayor frecuencia utilizando el paralaje anual , definido como la diferencia en la posición de una estrella vista desde la Tierra y el Sol, es decir, el ángulo subtendido en una estrella por el radio medio de la órbita de la Tierra alrededor del Sol. El pársec (3,26 años luz ) se define como la distancia para la cual el paralaje anual es 1  segundo de arco . El paralaje anual normalmente se mide observando la posición de una estrella en diferentes momentos del año a medida que la Tierra se mueve a través de su órbita.

Los ángulos involucrados en estos cálculos son muy pequeños y por lo tanto difíciles de medir. La estrella más cercana al Sol (y también la estrella con la mayor paralaje), Próxima Centauri , tiene un paralaje de 0,7685 ± 0,0002 segundos de arco. ^[19] Este ángulo es aproximadamente el que forma un objeto de 2 centímetros de diámetro ubicado a 5,3 kilómetros de distancia.

Para un triángulo rectángulo ,

${\displaystyle \tan p={\frac {1\,{\text{au}}}{d}},}$

donde es la paralaje, 1 ua (149.600.000 km) es aproximadamente la distancia media del Sol a la Tierra, y es la distancia a la estrella. Utilizando aproximaciones de ángulos pequeños (válidos cuando el ángulo es pequeño en comparación con 1 radián ),${\estilo de visualización p}$${\estilo de visualización d}$

${\displaystyle \tan x\approx x{\text{ radianes}}=x\cdot {\frac {180}{\pi }}{\text{ grados}}=x\cdot 180\cdot {\frac {3600}{\pi }}{\text{ segundos de arco}},}$

Entonces la paralaje, medida en segundos de arco, es

${\displaystyle p''\approx {\frac {1{\text{ au}}}{d}}\cdot 180\cdot {\frac {3600}{\pi }}.}$

Si el paralaje es 1", entonces la distancia es

${\displaystyle d=1{\text{ au}}\cdot 180\cdot {\frac {3600}{\pi }}\aproximadamente 206 265{\text{ au}}\aproximadamente 3,2616{\text{ ly}}\equiv 1{\text{ parsec}}.}$

Esto define el parsec , una unidad conveniente para medir la distancia utilizando paralaje. Por lo tanto, la distancia, medida en parsecs, es simplemente , cuando el paralaje se da en segundos de arco. ^[20]${\displaystyle d=1/p}$

Las mediciones precisas de paralaje de la distancia tienen un error asociado. Este error en el ángulo de paralaje medido no se traduce directamente en un error de distancia, excepto en el caso de errores relativamente pequeños. La razón de esto es que un error hacia un ángulo menor da como resultado un error mayor en la distancia que un error hacia un ángulo mayor.

Sin embargo, se puede calcular una aproximación del error de distancia mediante

${\displaystyle \delta d=\delta \left({1 \sobre p}\right)=\left|{\parcial \sobre \parcial p}\left({1 \sobre p}\right)\right|\delta p={\delta p \sobre p^{2}}}$

donde d es la distancia y p es el paralaje. La aproximación es mucho más precisa para errores de paralaje que son pequeños en relación con el paralaje que para errores relativamente grandes. Para obtener resultados significativos en astronomía estelar , el astrónomo holandés Floor van Leeuwen recomienda que el error de paralaje no sea más del 10% del paralaje total al calcular esta estimación de error. ^[21]

• Lugar aparente
• TAU (nave espacial) (un proyecto de misión espacial abandonado que habría utilizado paralaje)

• Dyson, FW (1915). "Medición de las distancias de las estrellas". El Observatorio . 38 : 292. Bibcode :1915Obs....38..292D.