Respuesta al impulso infinito

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Infinite impulse response" – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this message)

La respuesta al impulso infinita ( IIR ) es una propiedad que se aplica a muchos sistemas lineales invariantes en el tiempo que se distinguen por tener una respuesta al impulso que no se vuelve exactamente cero después de un cierto punto, sino que continúa indefinidamente. Esto contrasta con un sistema de respuesta al impulso finito (FIR), en el que la respuesta al impulso se vuelve exactamente cero en momentos durante un tiempo finito , por lo que tiene una duración finita. Ejemplos comunes de sistemas lineales invariantes en el tiempo son la mayoría de los filtros electrónicos y digitales . Los sistemas con esta propiedad se conocen como sistemas IIR o filtros IIR .${\displaystyle h(t)}$${\displaystyle t>T}$${\displaystyle T}$

En la práctica, la respuesta al impulso, incluso de los sistemas IIR, suele aproximarse a cero y puede despreciarse más allá de cierto punto. Sin embargo, los sistemas físicos que dan lugar a respuestas IIR o FIR son distintos, y ahí radica la importancia de la distinción. Por ejemplo, los filtros electrónicos analógicos compuestos de resistencias, condensadores y/o inductores (y quizás amplificadores lineales) son generalmente filtros IIR. Por otro lado, los filtros de tiempo discreto (normalmente filtros digitales) basados ​​en una línea de retardo con tomas que no emplean realimentación son necesariamente filtros FIR. Los condensadores (o inductores) del filtro analógico tienen una "memoria" y su estado interno nunca se relaja por completo después de un impulso (suponiendo el modelo clásico de condensadores e inductores donde se ignoran los efectos cuánticos). Pero en el último caso, después de que un impulso ha llegado al final de la línea de retardo con tomas, el sistema ya no tiene memoria de ese impulso y ha vuelto a su estado inicial; su respuesta al impulso más allá de ese punto es exactamente cero.

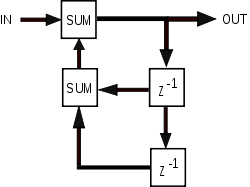
Aunque casi todos los filtros electrónicos analógicos son IIR, los filtros digitales pueden ser IIR o FIR. La presencia de retroalimentación en la topología de un filtro de tiempo discreto (como el diagrama de bloques que se muestra a continuación) generalmente crea una respuesta IIR. La función de transferencia del dominio z de un filtro IIR contiene un denominador no trivial, que describe esos términos de retroalimentación. La función de transferencia de un filtro FIR, por otro lado, solo tiene un numerador, como se expresa en la forma general derivada a continuación. Todos los coeficientes con (términos de retroalimentación) son cero y el filtro no tiene polos finitos .${\displaystyle a_{i}}$${\displaystyle i>0}$

Las funciones de transferencia pertenecientes a los filtros electrónicos analógicos IIR han sido ampliamente estudiadas y optimizadas para sus características de amplitud y fase. Estas funciones de filtro de tiempo continuo se describen en el dominio de Laplace . Las soluciones deseadas se pueden transferir al caso de filtros de tiempo discreto cuyas funciones de transferencia se expresan en el dominio z, mediante el uso de ciertas técnicas matemáticas como la transformada bilineal , la invariancia de impulsos o el método de coincidencia de polos y ceros . De este modo, los filtros IIR digitales se pueden basar en soluciones bien conocidas para filtros analógicos como el filtro de Chebyshev , el filtro Butterworth y el filtro elíptico , heredando las características de esas soluciones.

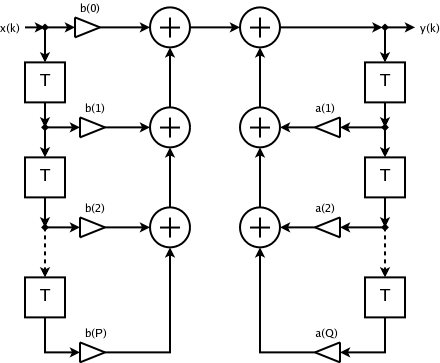
Los filtros digitales a menudo se describen e implementan en términos de la ecuación diferencial que define cómo se relaciona la señal de salida con la señal de entrada:

${\displaystyle {\begin{aligned}y[n]{}=&b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]\\&{}+a_{1}y[n-1]+a_{2}y[n-2]-\cdots +a_{Q}y[n-Q]\end{aligned}}}$

dónde:

• ${\displaystyle \ P}$¿Es el orden del filtro de avance?
• ${\displaystyle \ b_{i}}$son los coeficientes del filtro de avance
• ${\displaystyle \ Q}$¿Es el orden del filtro de retroalimentación?
• ${\displaystyle \ a_{i}}$son los coeficientes del filtro de retroalimentación
• ${\displaystyle \ x[n]}$es la señal de entrada
• ${\displaystyle \ y[n]}$es la señal de salida.

Una forma más condensada de la ecuación diferencial es:

${\displaystyle \ y[n]=\sum _{i=0}^{P}b_{i}x[n-i]+\sum _{i=1}^{Q}a_{i}y[n-i]}$

Para encontrar la función de transferencia del filtro, primero tomamos la transformada Z de cada lado de la ecuación anterior para obtener:

${\displaystyle \ Y(z)=X(z)\sum _{i=0}^{P}b_{i}z^{-i}+Y(z)\sum _{i=1}^{Q}a_{i}z^{-i}}$

Después de reorganizar:

${\displaystyle \ Y(z)\left[1-\sum _{i=1}^{Q}a_{i}z^{-i}\right]=X(z)\sum _{i=0}^{P}b_{i}z^{-i}}$

Luego definimos la función de transferencia como:

${\displaystyle H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{1-\sum _{i=1}^{Q}a_{i}z^{-i}}}}$

La función de transferencia permite juzgar si un sistema es estable en términos de entrada y salida acotadas (BIBO, por sus siglas en inglés) . Para ser más específicos, el criterio de estabilidad BIBO requiere que la ROC del sistema incluya el círculo unitario. Por ejemplo, para un sistema causal, todos los polos de la función de transferencia deben tener un valor absoluto menor que uno. En otras palabras, todos los polos deben estar ubicados dentro de un círculo unitario en el plano .${\displaystyle z}$

Los polos se definen como los valores cuyos denominador son iguales a 0:${\displaystyle z}$${\displaystyle H(z)}$

${\displaystyle \ 0=\sum _{j=0}^{Q}a_{j}z^{-j}}$

Es claro que, si los polos no están ubicados en el origen del plano , esto contrasta con el filtro FIR , donde todos los polos están ubicados en el origen y, por lo tanto, siempre es estable.${\displaystyle a_{j}\neq 0}$${\displaystyle z}$

A veces se prefieren los filtros IIR a los filtros FIR porque un filtro IIR puede lograr una reducción de la región de transición mucho más pronunciada que un filtro FIR del mismo orden.

Sea la función de transferencia de un filtro de tiempo discreto dada por:${\displaystyle H(z)}$

${\displaystyle H(z)={\frac {B(z)}{A(z)}}={\frac {1}{1-az^{-1}}}}$

gobernado por el parámetro , un número real con . es estable y causal con un polo en . Se puede demostrar que la respuesta al impulso en el dominio del tiempo está dada por:${\displaystyle a}$${\displaystyle 0<|a|<1}$${\displaystyle H(z)}$${\displaystyle a}$

${\displaystyle h(n)=a^{n}u(n)}$

donde es la función escalón unitario . Se puede ver que no es cero para todos , por lo tanto, una respuesta al impulso que continúa infinitamente.${\displaystyle u(n)}$${\displaystyle h(n)}$${\displaystyle n\geq 0}$

La principal ventaja que tienen los filtros IIR digitales sobre los filtros FIR es su eficiencia en la implementación, para cumplir con una especificación en términos de banda de paso, banda de rechazo, rizado y/o reducción gradual. Este conjunto de especificaciones se puede lograr con un filtro IIR de orden inferior ( Q en las fórmulas anteriores) al que se requeriría para un filtro FIR que cumpla con los mismos requisitos. Si se implementa en un procesador de señales, esto implica un número correspondientemente menor de cálculos por paso de tiempo; el ahorro computacional suele ser un factor bastante grande.

Por otra parte, los filtros FIR pueden ser más fáciles de diseñar, por ejemplo, para que se ajusten a un requisito de respuesta de frecuencia particular. Esto es particularmente cierto cuando el requisito no es uno de los casos habituales (paso alto, paso bajo, muesca, etc.) que se han estudiado y optimizado para filtros analógicos. Además, los filtros FIR se pueden hacer fácilmente para que sean de fase lineal ( retardo de grupo constante frente a frecuencia), una propiedad que no se cumple fácilmente utilizando filtros IIR y, en ese caso, solo como una aproximación (por ejemplo, con el filtro Bessel ). Otro problema con los filtros IIR digitales es el potencial de comportamiento de ciclo límite cuando están inactivos, debido al sistema de retroalimentación junto con la cuantificación.

La invariancia de impulso es una técnica para diseñar filtros de respuesta al impulso infinito (IIR) de tiempo discreto a partir de filtros de tiempo continuo en los que se muestrea la respuesta al impulso del sistema de tiempo continuo para producir la respuesta al impulso del sistema de tiempo discreto. La invariancia de impulso es uno de los métodos comúnmente utilizados para cumplir con los dos requisitos básicos del mapeo del plano s al plano z. Esto se obtiene resolviendo el T(z) que tiene el mismo valor de salida en el mismo tiempo de muestreo que el filtro analógico, y solo es aplicable cuando las entradas están en un pulso.
Tenga en cuenta que todas las entradas del filtro digital generado por este método son valores aproximados, excepto las entradas de pulso que son muy precisas. Este es el método de diseño de filtro IIR más simple. Es el más preciso a bajas frecuencias, por lo que generalmente se usa en filtros de paso bajo.

En el caso de la transformada de Laplace o transformada z, la salida después de la transformación es simplemente la entrada multiplicada por la función de transformación correspondiente, T(s) o T(z). Y(s) e Y(z) son la salida convertida de la entrada X(s) y la entrada X(z), respectivamente.

${\displaystyle Y(s)=T(s)X(s)}$

${\displaystyle Y(z)=T(z)X(z)}$

Al aplicar la transformada de Laplace o la transformada z en el impulso unitario, el resultado es 1. Por lo tanto, los resultados de salida después de la conversión son

${\displaystyle Y(s)=T(s)}$

${\displaystyle Y(z)=T(z)}$

Ahora la salida del filtro analógico es simplemente la transformada de Laplace inversa en el dominio del tiempo.

${\displaystyle y(t)=L^{-1}[Y(s)]=L^{-1}[T(s)]}$

Si usamos nT en lugar de t, podemos obtener la salida y(nT) derivada del pulso en el momento del muestreo. También se puede expresar como y(n)

${\displaystyle y(n)=y(nT)=y(t)|_{t=sT}}$

A esta señal de tiempo discreto se le puede aplicar la transformada z para obtener T(z)

${\displaystyle T(z)=Y(z)=Z[y(n)]}$

${\displaystyle T(z)=Z[y(n)]=Z[y(nT)]}$

${\displaystyle T(z)=Z\left\{L^{-1}[T(s)]_{t=nT}\right\}}$

La última ecuación describe matemáticamente que un filtro IIR digital debe realizar una transformación z en la señal analógica que ha sido muestreada y convertida a T(s) por Laplace, que generalmente se simplifica a

${\displaystyle T(z)=Z[T(s)]*T}$

Preste atención al hecho de que aparece un multiplicador T en la fórmula. Esto se debe a que, incluso si la transformada de Laplace y la transformada z para el pulso unitario son 1, el pulso en sí no es necesariamente el mismo. Para las señales analógicas, el pulso tiene un valor infinito, pero el área es 1 en t = 0, pero es 1 en el pulso de tiempo discreto t = 0, por lo que se requiere la existencia de un multiplicador T.

La invariancia de paso es un mejor método de diseño que la invariancia de impulso. El filtro digital tiene varios segmentos de entrada con diferentes constantes cuando se muestrea, que se compone de pasos discretos. El filtro IIR invariante de paso es menos preciso que la misma señal de paso de entrada al ADC. Sin embargo, es una mejor aproximación para cualquier entrada que el invariante de impulso.
La invariancia de paso resuelve el problema de los mismos valores de muestra cuando T(z) y T(s) son ambas entradas de paso. La entrada al filtro digital es u(n), y la entrada al filtro analógico es u(t). Aplique la transformada z y la transformada de Laplace en estas dos entradas para obtener la señal de salida convertida.
Realice la transformada z en la entrada de paso Salida convertida después de la transformada z Realice la transformada de Laplace en la entrada de paso Salida convertida después de la transformada de Laplace La salida del filtro analógico es y(t), que es la transformada de Laplace inversa de Y(s). Si se muestrea cada T segundos, es y(n), que es la conversión inversa de Y(z). Estas señales se utilizan para resolver el filtro digital y el filtro analógico y tienen la misma salida en el momento del muestreo. La siguiente ecuación señala la solución de T(z), que es la fórmula aproximada para el filtro analógico.${\displaystyle Z[u(n)]={\dfrac {z}{z-1}}}$
${\displaystyle Y(z)=T(z)U(z)=T(z){\dfrac {z}{z-1}}}$
${\displaystyle L[u(t)]={\dfrac {1}{s}}}$
${\displaystyle Y(s)=T(s)U(s)={\dfrac {T(s)}{s}}}$

${\displaystyle T(z)={\dfrac {z-1}{z}}Y(z)}$

${\displaystyle T(z)={\dfrac {z-1}{z}}Z[y(n)]}$

${\displaystyle T(z)={\dfrac {z-1}{z}}Z[Y(s)]}$

${\displaystyle T(z)={\dfrac {z-1}{z}}Z[{\dfrac {T(s)}{s}}]}$

La transformada bilineal es un caso especial de una aplicación conforme, que se utiliza a menudo para convertir una función de transferencia de un filtro lineal invariante en el tiempo (LTI) en el dominio del tiempo continuo (a menudo llamado filtro analógico) en una función de transferencia de un filtro lineal invariante en el desplazamiento en el dominio del tiempo discreto. La transformada bilineal es una aproximación de primer orden de la función logaritmo natural que es una aplicación exacta del plano z al plano s . Cuando se realiza la transformada de Laplace en una señal de tiempo discreto (con cada elemento de la secuencia de tiempo discreto unido a un impulso unitario retardado correspondiente), el resultado es precisamente la transformada Z de la secuencia de tiempo discreto con la sustitución de${\displaystyle H_{a}(s)}$${\displaystyle H_{d}(z)}$

${\displaystyle {\begin{aligned}z&=e^{sT}\\&={\frac {e^{sT/2}}{e^{-sT/2}}}\\&\approx {\frac {1+sT/2}{1-sT/2}}\end{aligned}}}$

donde es el tamaño del paso de integración numérica de la regla trapezoidal utilizada en la derivación de la transformada bilineal; o, en otras palabras, el período de muestreo. La aproximación bilineal anterior se puede resolver para o se puede realizar una aproximación similar para .${\displaystyle T}$${\displaystyle s}$${\displaystyle s=(1/T)\ln(z)}$

La inversa de esta aplicación (y su aproximación bilineal de primer orden) es

${\displaystyle {\begin{aligned}s&={\frac {1}{T}}\ln(z)\\&={\frac {2}{T}}\left[{\frac {z-1}{z+1}}+{\frac {1}{3}}\left({\frac {z-1}{z+1}}\right)^{3}+{\frac {1}{5}}\left({\frac {z-1}{z+1}}\right)^{5}+{\frac {1}{7}}\left({\frac {z-1}{z+1}}\right)^{7}+\cdots \right]\\&\approx {\frac {2}{T}}{\frac {z-1}{z+1}}\\&={\frac {2}{T}}{\frac {1-z^{-1}}{1+z^{-1}}}\end{aligned}}}$

Esta relación se utiliza en la función de transferencia de Laplace de cualquier filtro analógico o en el filtro de respuesta al impulso infinito (IIR) digital T(z) del filtro analógico.
La transformada bilineal utiliza esencialmente esta aproximación de primer orden y la sustituye en la función de transferencia de tiempo continuo,${\displaystyle H_{a}(s)}$

${\displaystyle s\leftarrow {\frac {2}{T}}{\frac {z-1}{z+1}}.}$

Eso es

${\displaystyle H_{d}(z)=H_{a}(s){\bigg |}_{s={\frac {2}{T}}{\frac {z-1}{z+1}}}=H_{a}\left({\frac {2}{T}}{\frac {z-1}{z+1}}\right).\ }$

que se utiliza para calcular el filtro digital IIR, a partir de la función de transferencia de Laplace del filtro analógico.

• Modelo autorregresivo
• Filtro electrónico
• Respuesta de impulso finito
• Relación de recurrencia , formalización matemática
• Análisis del sistema

• El quinto módulo del curso de procesamiento de señales DSP de BORES: Introducción al DSP] ​​en ​​Wayback Machine (archivado el 2 de julio de 2016)
• Subprograma de diseño de filtros digitales IIR en Wayback Machine (archivado el 13 de febrero de 2010)
• Herramienta de diseño de filtros digitales IIR Archivado el 30 de agosto de 2020 en Wayback Machine : produce coeficientes, gráficos, polos, ceros y código C
• Herramienta de diseño IIR en línea EngineerJS: no requiere Java