Inferencia algorítmica

La inferencia algorítmica recoge los nuevos desarrollos en los métodos de inferencia estadística que se han hecho posibles gracias a los potentes dispositivos informáticos de los que dispone cualquier analista de datos. Las piedras angulares de este campo son la teoría del aprendizaje computacional , la computación granular , la bioinformática y, hace mucho tiempo, la probabilidad estructural (Fraser 1966). El enfoque principal se centra en los algoritmos que calculan las estadísticas que fundamentan el estudio de un fenómeno aleatorio, junto con la cantidad de datos que deben alimentar para producir resultados fiables. Esto desplaza el interés de los matemáticos desde el estudio de las leyes de distribución hacia las propiedades funcionales de las estadísticas , y el interés de los informáticos desde los algoritmos para procesar datos hacia la información que procesan.

En lo que respecta a la identificación de los parámetros de una ley de distribución, el lector maduro puede recordar largas disputas a mediados del siglo XX sobre la interpretación de su variabilidad en términos de distribución fiducial (Fisher 1956), probabilidades estructurales (Fraser 1966), probabilidades previas/posteriores (Ramsey 1925), etc. Desde un punto de vista epistemológico , esto implicó una disputa paralela sobre la naturaleza de la probabilidad : ¿es una característica física de los fenómenos que se describe a través de variables aleatorias o una forma de sintetizar datos sobre un fenómeno? Optando por esto último, Fisher define una ley de distribución fiducial de los parámetros de una variable aleatoria dada que deduce de una muestra de sus especificaciones. Con esta ley calcula, por ejemplo, "la probabilidad de que μ (media de una variable gaussiana - nota al pie) sea menor que cualquier valor asignado, o la probabilidad de que se encuentre entre cualquier valor asignado, o, en resumen, su distribución de probabilidad, a la luz de la muestra observada".

Fisher luchó mucho para defender la diferencia y superioridad de su noción de distribución de parámetros en comparación con nociones análogas, como la distribución posterior de Bayes , la probabilidad constructiva de Fraser y los intervalos de confianza de Neyman . Durante medio siglo, los intervalos de confianza de Neyman ganaron para todos los fines prácticos, dando crédito a la naturaleza fenomenológica de la probabilidad. Con esta perspectiva, cuando se trabaja con una variable gaussiana, su media μ está fijada por las características físicas del fenómeno que se está observando, donde las observaciones son operadores aleatorios, por lo tanto, los valores observados son especificaciones de una muestra aleatoria . Debido a su aleatoriedad, se pueden calcular a partir de la muestra intervalos específicos que contienen el μ fijo con una probabilidad dada que denota confianza .

Sea X una variable gaussiana ^[1] con parámetros y y una muestra extraída de ella. Trabajar con estadísticas${\estilo de visualización \mu}$${\displaystyle \sigma ^{2}}$${\displaystyle \{X_{1},\ldots ,X_{m}\}}$

${\displaystyle S_{\mu}=\sum _{i=1}^{m}X_{i}}$

y

${\displaystyle S_{\sigma ^{2}}=\sum _{i=1}^{m}(X_{i}-{\overline {X}})^{2},{\text{ donde }}{\overline {X}}={\frac {S_{\mu }}{m}}}$

es la media de la muestra, reconocemos que

${\displaystyle T={\frac {S_{\mu }-m\mu }{\sqrt {S_{\sigma ^{2}}}}}{\sqrt {\frac {m-1}{m}}}={\frac {{\overline {X}}-\mu }{\sqrt {S_{\sigma ^{2}}/(m(m-1))}}}}$

sigue una distribución t de Student (Wilks 1962) con parámetro (grados de libertad) m  − 1, de modo que

${\displaystyle f_{T}(t)={\frac {\Gamma (m/2)}{\Gamma ((m-1)/2)}}{\frac {1}{\sqrt {\pi (m-1)}}}\left(1+{\frac {t^{2}}{m-1}}\right)^{m/2}.}$

Al medir T entre dos cuantiles e invertir su expresión en función de se obtienen intervalos de confianza para .${\estilo de visualización \mu}$${\estilo de visualización \mu}$

Con la especificación de muestra:

${\displaystyle \mathbf {x} =\{7,14,6,3,3,9,6,46,0,2,2,94,4,14,4,69,6,02,1,58\}}$

teniendo un tamaño m = 10, calcula las estadísticas y , y obtiene un intervalo de confianza de 0,90 para con extremos (3,03, 5,65).${\displaystyle s_{\mu}=43,37}$${\displaystyle s_{\sigma ^{2}}=46,07}$${\estilo de visualización \mu}$

Desde una perspectiva de modelado, toda la disputa parece un dilema del huevo y la gallina: o bien los datos fijos como primer paso y la distribución de probabilidad de sus propiedades como consecuencia, o bien las propiedades fijas como primer paso y la distribución de probabilidad de los datos observados como corolario. La solución clásica tiene un beneficio y un inconveniente. La primera era apreciada particularmente cuando la gente todavía hacía cálculos con papel y lápiz. En sí, la tarea de calcular un intervalo de confianza de Neyman para el parámetro fijo θ es difícil: no se conoce θ, pero se busca disponer alrededor de él un intervalo con una probabilidad posiblemente muy baja de fallar. La solución analítica está permitida para un número muy limitado de casos teóricos. Viceversa, una gran variedad de casos se pueden resolver rápidamente de manera aproximada a través del teorema del límite central en términos de intervalo de confianza alrededor de una distribución gaussiana: esa es la ventaja. El inconveniente es que el teorema del límite central es aplicable cuando el tamaño de la muestra es suficientemente grande. Por lo tanto, es cada vez menos aplicable con la muestra involucrada en los casos de inferencia modernos. La falla no está en el tamaño de la muestra en sí. Más bien, este tamaño no es suficientemente grande debido a la complejidad del problema de inferencia.

Con la disponibilidad de grandes instalaciones informáticas, los científicos reorientaron su enfoque desde la inferencia de parámetros aislados hacia la inferencia de funciones complejas, es decir, conjuntos de parámetros altamente anidados que identifican funciones. En estos casos hablamos de aprendizaje de funciones (en términos, por ejemplo, de regresión , sistema neurodifuso o aprendizaje computacional ) sobre la base de muestras altamente informativas. Un primer efecto de tener una estructura compleja que vincula los datos es la reducción del número de grados de libertad de la muestra , es decir, la quema de una parte de los puntos de muestra, de modo que el tamaño de muestra efectivo a considerar en el teorema del límite central es demasiado pequeño. Al centrarse en el tamaño de la muestra que garantiza un error de aprendizaje limitado con un nivel de confianza dado , la consecuencia es que el límite inferior de este tamaño crece con los índices de complejidad, como la dimensión VC o el detalle de una clase a la que pertenece la función que queremos aprender.

Una muestra de 1.000 bits independientes es suficiente para asegurar un error absoluto de como máximo 0,081 en la estimación del parámetro p de la variable de Bernoulli subyacente con una confianza de al menos 0,99. El mismo tamaño no puede garantizar un umbral inferior a 0,088 con la misma confianza 0,99 cuando el error se identifica con la probabilidad de que un hombre de 20 años que vive en Nueva York no se ajuste a los rangos de altura, peso y cintura observados en 1.000 habitantes de la Gran Manzana. La falta de precisión se produce porque tanto la dimensión del VC como el detalle de la clase de paralelepípedos, entre los que se encuentra el observado a partir de los rangos de 1.000 habitantes, son iguales a 6.

Con muestras insuficientemente grandes, el enfoque muestra fija – propiedades aleatorias sugiere procedimientos de inferencia en tres pasos:

1.	Mecanismo de muestreo . Consiste en un par , donde la semilla Z es una variable aleatoria sin parámetros desconocidos, mientras que la función explicativa es una función que mapea de muestras de Z a muestras de la variable aleatoria X que nos interesa. El vector de parámetros es una especificación del parámetro aleatorio . Sus componentes son los parámetros de la ley de distribución X. El Teorema de la Transformada Integral asegura la existencia de tal mecanismo para cada X (escalar o vectorial) cuando la semilla coincide con la variable aleatoria U uniformemente distribuida en .${\displaystyle (Z,g_{\boldsymbol {\theta }})}$${\displaystyle g_{\boldsymbol {\theta}}}$${\displaystyle {\boldsymbol {\theta }}}$${\displaystyle \mathbf {\Theta}}$ ${\estilo de visualización [0,1]}$ Ejemplo. Para X que sigue una distribución de Pareto con parámetros a y k , es decir ${\displaystyle F_{X}(x)=\left(1-{\frac {k}{x}}^{a}\right)I_{[k,\infty )}(x),}$ Un mecanismo de muestreo para X con semilla U dice:${\displaystyle (U,g_{(a,k)})}$ ${\displaystyle g_{(a,k)}(u)=k(1-u)^{-{\frac {1}{a}}},}$ o, equivalentemente,${\displaystyle g_{(a,k)}(u)=ku^{-1/a}.}$
2.	Ecuaciones maestras . La conexión real entre el modelo y los datos observados se plantea en términos de un conjunto de relaciones entre las estadísticas de los datos y los parámetros desconocidos que surgen como corolario de los mecanismos de muestreo. Llamamos a estas relaciones ecuaciones maestras . En torno a la estadística , la forma general de una ecuación maestra es:${\displaystyle s=h(x_{1},\ldots ,x_{m})=h(g_{\boldsymbol {\theta }}(z_{1}),\ldots ,g_{\boldsymbol {\theta }}(z_{m}))}$ ${\displaystyle s=\rho ({\boldsymbol {\theta }};z_{1},\ldots ,z_{m})}$. Con estas relaciones podemos inspeccionar los valores de los parámetros que podrían haber generado una muestra con la estadística observada a partir de un conjunto particular de semillas que representan la semilla de la muestra. Por lo tanto, a la población de semillas de la muestra le corresponde una población de parámetros. Para asegurar que esta población tenga propiedades limpias, es suficiente extraer aleatoriamente los valores de las semillas e involucrar estadísticas suficientes o, simplemente, estadísticas que se comporten bien con respecto a los parámetros, en las ecuaciones maestras. Por ejemplo, las estadísticas y resultan suficientes para los parámetros a y k de una variable aleatoria de Pareto X. Gracias al mecanismo de muestreo (forma equivalente del) podemos leerlas como${\displaystyle s_{1}=\suma _{i=1}^{m}\log x_{i}}$${\displaystyle s_{2}=\min _{i=1,\ldots ,m}\{x_{i}\}}$$estilo de visualización g_{(a,k)}}$ ${\displaystyle s_{1}=m\log k+1/a\sum _{i=1}^{m}\log u_{i}}$ ${\displaystyle s_{2}=\min _{i=1,\ldots ,m}\{ku_{i}^{-{\frac {1}{a}}}\},}$ respectivamente.
3.	Población de parámetros . Una vez que se ha fijado un conjunto de ecuaciones maestras, se pueden asignar semillas de muestra a parámetros, ya sea numéricamente a través de un bootstrap de población o analíticamente a través de un argumento de torsión . Por lo tanto, a partir de una población de semillas se obtiene una población de parámetros. Ejemplo. De la ecuación maestra anterior podemos extraer un par de parámetros, , compatibles con la muestra observada, resolviendo el siguiente sistema de ecuaciones:${\estilo de visualización (a,k)}$ ${\displaystyle a={\frac {\sum \log u_{i}-m\log \min\{u_{i}\}}{s_{1}-m\log s_{2}}}.}$ ${\displaystyle k=\mathrm {e} ^{\frac {as_{1}-\sum \log u_{i}}{ma}}}$ donde y son las estadísticas observadas y un conjunto de semillas uniformes. Al transferir a los parámetros la probabilidad (densidad) que afecta a las semillas, se obtiene la ley de distribución de los parámetros aleatorios A y K compatible con las estadísticas que se han observado.$estilo de visualización s_{1}$$estilo de visualización s_{2}$${\displaystyle u_{1},\ldots ,u_{m}}$ La compatibilidad denota parámetros de poblaciones compatibles, es decir, de poblaciones que podrían haber generado una muestra que dé lugar a las estadísticas observadas. Se puede formalizar esta noción de la siguiente manera:

Para una variable aleatoria y una muestra extraída de ella,Una distribución compatible es una distribución que tiene el mismo mecanismo de muestreo de X con un valor del parámetro aleatorio derivado de una ecuación maestra basada en una estadística de buen comportamiento s .${\displaystyle {\mathcal {M}}_{X}=(Z,g_{\boldsymbol {\theta }})}$${\displaystyle {\boldsymbol {\theta }}}$${\displaystyle \mathbf {\Theta}}$

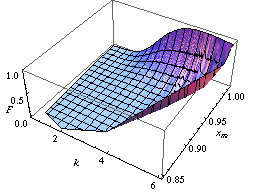
Puede encontrar la ley de distribución de los parámetros de Pareto A  y K  como un ejemplo de implementación del método bootstrap de población  como en la figura de la izquierda.

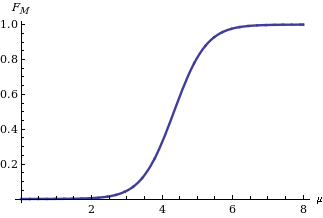
Implementando el método de argumentos torcidos  , se obtiene la ley de distribución  de la media M  de una variable gaussiana X  sobre la base del estadístico  cuando  se sabe que es igual a  (Apolloni, Malchiodi y Gaito 2006). Su expresión es:${\displaystyle F_{M}(\mu )}$${\displaystyle s_{M}=\sum _{i=1}^{m}x_{i}}$$Estilo de visualización: Sigma ^{2}}$${\displaystyle \sigma ^{2}}$

${\displaystyle F_{M}(\mu )=\Phi \left({\frac {m\mu -s_{M}}{\sigma {\sqrt {m}}}}\right),}$

Como se muestra en la figura de la derecha, donde es la función de distribución acumulativa de una distribución normal estándar .${\estilo de visualización \Phi}$

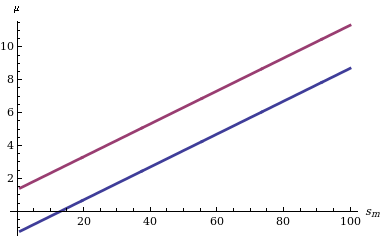
Calcular un intervalo de confianza  para M  dada su función de distribución es sencillo: solo necesitamos encontrar dos cuantiles (por ejemplo,  y  cuantiles en caso de que estemos interesados ​​en un intervalo de confianza de nivel δ simétrico en las probabilidades de la cola) como se indica a la izquierda en el diagrama que muestra el comportamiento de los dos límites para diferentes valores del estadístico s _m .${\displaystyle \delta /2}$${\displaystyle 1-\delta /2}$

El talón de Aquiles del enfoque de Fisher reside en la distribución conjunta de más de un parámetro, por ejemplo, la media y la varianza de una distribución gaussiana. Por el contrario, con el último enfoque (y los métodos mencionados anteriormente: el bootstrap de población y el argumento de torsión ) podemos aprender la distribución conjunta de muchos parámetros. Por ejemplo, centrándonos en la distribución de dos o más parámetros, en las figuras siguientes informamos de dos regiones de confianza en las que la función que se va a aprender cae con una confianza del 90%. La primera se refiere a la probabilidad con la que una máquina de vectores de soporte extendida atribuye una etiqueta binaria 1 a los puntos del plano. Las dos superficies se dibujan sobre la base de un conjunto de puntos de muestra etiquetados a su vez de acuerdo con una ley de distribución específica (Apolloni et al. 2008). La última se refiere a la región de confianza de la tasa de riesgo de recurrencia del cáncer de mama calculada a partir de una muestra censurada (Apolloni, Malchiodi y Gaito 2006).${\estilo de visualización (x,y)}$

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2011) (Learn how and when to remove this message)

• Fraser, DAS (1966), "Probabilidad estructural y generalización", Biometrika , 53 (1/2): 1–9, doi :10.2307/2334048, JSTOR  2334048.
• Fisher, MA (1956), Métodos estadísticos e inferencia científica, Edimburgo y Londres: Oliver y Boyd
• Apolloni, B.; Malchiodi, D.; Gaito, S. (2006), Inferencia algorítmica en aprendizaje automático , International Series on Advanced Intelligence, vol. 5 (2.ª ed.), Adelaide: Magill, Advanced Knowledge International
• Apolloni, B.; Bassis, S.; Malchiodi, D.; Witold, P. (2008), El rompecabezas de la computación granular, Estudios en inteligencia computacional, vol. 138, Berlín: Springer, ISBN 9783540798637
• Ramsey, FP (1925), "Los fundamentos de las matemáticas", Actas de la London Mathematical Society : 338–384, doi :10.1112/plms/s2-25.1.338.
• Wilks, SS (1962), Estadística matemática , Wiley Publications in Statistics, Nueva York: John Wiley