Sistema de navegación inercial

La introducción de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave . Considere ampliar la introducción para brindar una descripción general accesible de todos los aspectos importantes del artículo. ( Septiembre de 2023 )

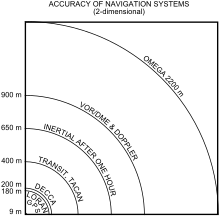
Un sistema de navegación inercial ( INS ; también sistema de guía inercial , instrumento inercial ) es un dispositivo de navegación que utiliza sensores de movimiento ( acelerómetros ), sensores de rotación ( giroscopios ) y una computadora para calcular continuamente por estima la posición, la orientación y la velocidad (dirección y velocidad de movimiento) de un objeto en movimiento sin la necesidad de referencias externas. ^[1] A menudo, los sensores inerciales se complementan con un altímetro barométrico y, a veces, con sensores magnéticos ( magnetómetros ) y/o dispositivos de medición de velocidad. Los INS se utilizan en robots móviles ^{[2] [3]} y en vehículos como barcos , aviones , submarinos , misiles guiados y naves espaciales . ^[4] Los sistemas INS más antiguos generalmente usaban una plataforma inercial como punto de montaje en el vehículo y, a veces, los términos se consideran sinónimos.

Las integrales en el dominio del tiempo exigen implícitamente un reloj estable y preciso para la cuantificación del tiempo transcurrido.

La navegación inercial es una técnica de navegación autónoma en la que se utilizan las mediciones proporcionadas por acelerómetros y giroscopios para rastrear la posición y la orientación de un objeto en relación con un punto de partida, una orientación y una velocidad conocidos. Las unidades de medición inercial (IMU) suelen contener tres giroscopios de velocidad ortogonal y tres acelerómetros ortogonales, que miden la velocidad angular y la aceleración lineal respectivamente. Al procesar las señales de estos dispositivos, es posible rastrear la posición y la orientación de un dispositivo.

Un sistema de navegación inercial incluye al menos un ordenador y una plataforma o módulo que contiene acelerómetros , giroscopios u otros dispositivos de detección de movimiento. El INS recibe inicialmente su posición y velocidad de otra fuente (un operador humano, un receptor de satélite GPS, etc.) acompañada de la orientación inicial y, a continuación, calcula su propia posición y velocidad actualizadas integrando la información recibida de los sensores de movimiento. La ventaja de un INS es que no requiere referencias externas para determinar su posición, orientación o velocidad una vez que se ha inicializado.

Un INS puede detectar un cambio en su posición geográfica (un movimiento hacia el este o el norte, por ejemplo), un cambio en su velocidad (velocidad y dirección del movimiento) y un cambio en su orientación (rotación sobre un eje). Lo hace midiendo la aceleración lineal y la velocidad angular aplicadas al sistema. Como no requiere ninguna referencia externa (después de la inicialización), es inmune a interferencias y engaños.

Los giroscopios miden el desplazamiento angular del marco del sensor con respecto al marco de referencia inercial . Al utilizar la orientación original del sistema en el marco de referencia inercial como condición inicial e integrar el desplazamiento angular, se conoce en todo momento la orientación actual del sistema. Esto se puede considerar como la capacidad de un pasajero con los ojos vendados en un automóvil de sentir que el automóvil gira a la izquierda y a la derecha o se inclina hacia arriba y hacia abajo a medida que asciende o desciende colinas. Basándose únicamente en esta información, el pasajero sabe en qué dirección está orientado el automóvil, pero no a qué velocidad o a qué lentitud se mueve, o si se desliza hacia los lados.

Los acelerómetros miden la aceleración lineal del vehículo en movimiento en el sensor o en el marco de la carrocería, pero en direcciones que solo se pueden medir en relación con el sistema en movimiento (ya que los acelerómetros están fijados al sistema y giran con el sistema, pero no son conscientes de su propia orientación). Esto se puede considerar como la capacidad de un pasajero con los ojos vendados en un automóvil de sentirse presionado hacia atrás en su asiento cuando el vehículo acelera hacia adelante o tirado hacia adelante cuando disminuye la velocidad; y sentirse presionado hacia abajo en su asiento cuando el vehículo acelera cuesta arriba o levantarse de su asiento cuando el automóvil pasa por la cresta de una colina y comienza a descender. Basándose solo en esta información, saben cómo acelera el vehículo en relación con sí mismo; es decir, si está acelerando hacia adelante, hacia atrás, hacia la izquierda, hacia la derecha, hacia arriba (hacia el techo del automóvil) o hacia abajo (hacia el piso del automóvil), medido en relación con el automóvil, pero no la dirección relativa a la Tierra, ya que no sabían en qué dirección estaba orientado el automóvil en relación con la Tierra cuando sintieron las aceleraciones.

Sin embargo, al rastrear tanto la velocidad angular actual del sistema como la aceleración lineal actual del sistema medida en relación con el sistema en movimiento, es posible determinar la aceleración lineal del sistema en el marco de referencia inercial. Realizar la integración en las aceleraciones inerciales (usando la velocidad original como condición inicial) utilizando las ecuaciones cinemáticas correctas produce las velocidades inerciales del sistema y la integración nuevamente (usando la posición original como condición inicial) produce la posición inercial. En nuestro ejemplo, si el pasajero con los ojos vendados sabía cómo apuntaba el automóvil y cuál era su velocidad antes de que le vendaran los ojos, y si puede realizar un seguimiento tanto de cómo ha girado el automóvil como de cómo ha acelerado y desacelerado desde entonces, entonces puede saber con precisión la orientación, posición y velocidad actuales del automóvil en cualquier momento.

La navegación inercial se utiliza en una amplia gama de aplicaciones, incluida la navegación de aeronaves, misiles tácticos y estratégicos, naves espaciales, submarinos y barcos. También está integrada en algunos teléfonos móviles con fines de localización y seguimiento de teléfonos móviles. ^{[5] [6]} Los avances recientes en la construcción de sistemas microelectromecánicos (MEMS) han hecho posible la fabricación de sistemas de navegación inercial pequeños y ligeros. Estos avances han ampliado la gama de posibles aplicaciones para incluir áreas como la captura de movimiento humano y animal .

Los sistemas de navegación inercial se utilizan en muchos objetos móviles diferentes. Sin embargo, su coste y complejidad imponen limitaciones a los entornos en los que se pueden utilizar de forma práctica.

Para apoyar el uso de la tecnología inercial de la mejor manera, ya en 1965 se creó en Alemania un grupo de trabajo técnico sobre sensores inerciales que reunía a los usuarios, fabricantes e investigadores de sensores inerciales. Este grupo de trabajo se ha ido desarrollando continuamente y hoy se conoce como DGON ISA Inertial Sensors and Application Symposium, la conferencia líder sobre tecnologías inerciales desde hace más de 60 años. Este simposio DGON / IEEE ISA con alrededor de 200 asistentes internacionales se celebra anualmente en octubre en Alemania. Las publicaciones de todas las conferencias DGON ISA de los últimos más de 60 años están disponibles.

Todos los sistemas de navegación inercial sufren de deriva de integración: pequeños errores en la medición de la aceleración y la velocidad angular se integran en errores progresivamente mayores en la velocidad, que se combinan para generar errores aún mayores en la posición. ^{[7] [8]} Dado que la nueva posición se calcula a partir de la posición calculada previamente y la aceleración y la velocidad angular medidas, estos errores se acumulan aproximadamente de manera proporcional al tiempo transcurrido desde que se introdujo la posición inicial. Incluso los mejores acelerómetros, con un error estándar de 10 micro-g, acumularían un error de 50 metros (164 pies) en 17 minutos. ^[9] Por lo tanto, la posición debe corregirse periódicamente mediante la entrada de algún otro tipo de sistema de navegación.

En consecuencia, la navegación inercial se utiliza habitualmente para complementar otros sistemas de navegación, proporcionando un mayor grado de precisión que el que es posible con el uso de un solo sistema. Por ejemplo, si, en el uso terrestre, la velocidad rastreada inercialmente se actualiza intermitentemente a cero mediante una parada, la posición permanecerá precisa durante un tiempo mucho más largo, una llamada actualización de velocidad cero . En el sector aeroespacial en particular, se utilizan otros sistemas de medición para determinar las imprecisiones del INS, por ejemplo, los sistemas de navegación inercial Honeywell LaseRefV utilizan salidas de computadora de datos aéreos y GPS para mantener el rendimiento de navegación requerido . El error de navegación aumenta con la menor sensibilidad de los sensores utilizados. Actualmente, se están desarrollando dispositivos que combinan diferentes sensores, por ejemplo, el sistema de referencia de actitud y rumbo . Debido a que el error de navegación está influenciado principalmente por la integración numérica de las velocidades angulares y las aceleraciones, el sistema de referencia de presión se desarrolló para utilizar una integración numérica de las mediciones de velocidad angular.

La teoría de estimación en general y el filtrado de Kalman en particular, ^[10] proporcionan un marco teórico para combinar información de varios sensores. Uno de los sensores alternativos más comunes es una radio de navegación por satélite como GPS , que se puede utilizar para todo tipo de vehículos con visibilidad directa del cielo. Las aplicaciones en interiores pueden utilizar podómetros , equipos de medición de distancia u otros tipos de sensores de posición . Al combinar adecuadamente la información de un INS y otros sistemas ( GPS ), los errores de posición y velocidad son estables . Además, el INS se puede utilizar como una alternativa a corto plazo mientras las señales GPS no están disponibles, por ejemplo, cuando un vehículo pasa por un túnel.

En 2011, la interferencia del GPS a nivel civil se convirtió en una preocupación gubernamental. ^[11] La relativa facilidad para interferir estos sistemas ha motivado a los militares a reducir la dependencia de la tecnología GPS en la navegación. ^[12] Debido a que los sensores de navegación inercial no dependen de señales de radio a diferencia del GPS, no pueden ser interferidos. ^[13] En 2012, el Laboratorio de Investigación del Ejército de los EE. UU. informó sobre un método para fusionar mediciones de 10 pares de giroscopios y acelerómetros MEMS (más GPS ocasional), reduciendo el error de posición en dos tercios para un proyectil. El algoritmo puede corregir sesgos sistémicos en sensores individuales, utilizando tanto el GPS como una heurística basada en la fuerza de aceleración del disparo del arma. Si un sensor sobreestima o subestima constantemente la distancia, el sistema puede ajustar las contribuciones del sensor dañado al cálculo final. ^[14]

The examples and perspective in this section deal primarily with the United States and do not represent a worldwide view of the subject. You may improve this section, discuss the issue on the talk page, or create a new section, as appropriate. (January 2015) (Learn how and when to remove this message)

Los sistemas de navegación inercial se desarrollaron originalmente para cohetes . El pionero estadounidense de la cohetería Robert Goddard experimentó con sistemas giroscópicos rudimentarios. Los sistemas de Goddard fueron de gran interés para los pioneros alemanes contemporáneos, entre ellos Wernher von Braun . Los sistemas entraron en un uso más generalizado con la llegada de las naves espaciales , los misiles guiados y los aviones comerciales .

Los primeros sistemas de guía alemanes V2 de la Segunda Guerra Mundial combinaban dos giroscopios y un acelerómetro lateral con una computadora analógica simple para ajustar el acimut del cohete en vuelo. Las señales de la computadora analógica se usaban para impulsar cuatro timones de grafito en el escape del cohete para el control del vuelo. El sistema GN&C (Guía, Navegación y Control) para el V2 proporcionó muchas innovaciones como plataforma integrada con guía de bucle cerrado. Al final de la guerra, von Braun diseñó la rendición de 500 de sus principales científicos de cohetes, junto con planes y vehículos de prueba, a los estadounidenses. Llegaron a Fort Bliss, Texas, en 1945 bajo las disposiciones de la Operación Paperclip y posteriormente fueron trasladados a Huntsville, Alabama , en 1950 ^[15] donde trabajaron para los programas de investigación de cohetes del Ejército de los EE. UU.

A principios de los años 50, el gobierno de Estados Unidos quería protegerse de una dependencia excesiva del equipo alemán para aplicaciones militares, incluido el desarrollo de un programa de guía de misiles totalmente nacional. El Laboratorio de Instrumentación del MIT (que más tarde se convertiría en el Laboratorio Charles Stark Draper , Inc.) fue elegido por la División de Desarrollo Occidental de la Fuerza Aérea para proporcionar un sistema de guía autónomo de respaldo a Convair en San Diego para el nuevo misil balístico intercontinental Atlas ^{[16] [17] [18] [19]} (La construcción y las pruebas fueron completadas por la División Arma de AmBosch Arma). El supervisor técnico de la tarea del MIT fue el ingeniero Jim Fletcher, quien más tarde se desempeñó como administrador de la NASA. El sistema de guía Atlas iba a ser una combinación de un sistema autónomo de a bordo y un sistema de seguimiento y comando basado en tierra. El sistema autónomo finalmente prevaleció en aplicaciones de misiles balísticos por razones obvias. En la exploración espacial, sigue habiendo una mezcla de los dos.

En el verano de 1952, el Dr. Richard Battin y el Dr. J. Halcombe "Hal" Laning, Jr. investigaron soluciones basadas en computación para el guiado y emprendieron el trabajo analítico inicial sobre el guiado inercial Atlas en 1954. Otras figuras clave en Convair fueron Charlie Bossart, el ingeniero jefe, y Walter Schweidetzky, jefe del grupo de guiado. Schweidetzky había trabajado con von Braun en Peenemünde durante la Segunda Guerra Mundial.

El sistema de guía inicial de Delta evaluó la diferencia de posición con respecto a una trayectoria de referencia. Se realizó un cálculo de velocidad a ganar (VGO) para corregir la trayectoria actual con el objetivo de llevar la VGO a cero. Las matemáticas de este enfoque eran fundamentalmente válidas, pero se abandonaron debido a los desafíos en la guía inercial precisa y la potencia de cálculo analógica. Los desafíos que enfrentaron los esfuerzos de Delta fueron superados por el sistema Q (ver Q-guidance ) de guía. La revolución del sistema Q fue unir los desafíos de la guía de misiles (y las ecuaciones de movimiento asociadas) en la matriz Q. La matriz Q representa las derivadas parciales de la velocidad con respecto al vector de posición. Una característica clave de este enfoque permitió que los componentes del producto vectorial (v, xdv, /dt) se usaran como señales básicas de velocidad del piloto automático, una técnica que se conoció como dirección de producto vectorial . El sistema Q se presentó en el primer Simposio Técnico sobre Misiles Balísticos, celebrado en la Corporación Ramo-Wooldridge en Los Ángeles los días 21 y 22 de junio de 1956. El sistema Q fue información clasificada hasta la década de 1960. Las derivaciones de esta guía se utilizan para los misiles actuales.

En febrero de 1961, la NASA le otorgó al MIT un contrato para el estudio preliminar del diseño de un sistema de guía y navegación para el programa Apolo . El MIT y la División Electrónica Delco de General Motors Corp. obtuvieron el contrato conjunto para el diseño y la producción de los sistemas de guía y navegación Apolo para el módulo de mando y el módulo lunar. Delco produjo las IMU ( unidades de medición inercial ) para estos sistemas, Kollsman Instrument Corp. produjo los sistemas ópticos y la computadora de guía Apolo fue construida por Raytheon bajo subcontrato. ^{[20] [21]}

En el caso del transbordador espacial , se utilizó un sistema de guía de bucle abierto para guiar al transbordador desde el despegue hasta la separación del cohete propulsor sólido (SRB). Después de la separación del SRB, el sistema de guía principal del transbordador espacial se denomina PEG (Powered Explicit Guidance). El PEG tiene en cuenta tanto el sistema Q como los atributos predictores-correctores del sistema "Delta" original (PEG Guidance). Aunque se han realizado muchas actualizaciones del sistema de navegación del transbordador en los últimos 30 años (por ejemplo, el GPS en la versión OI-22), el núcleo de guía del sistema GN&C del transbordador había evolucionado poco. En un sistema tripulado, se necesita una interfaz humana para el sistema de guía. Como los astronautas son los clientes del sistema, se formaron muchos equipos nuevos que tocan GN&C, ya que es una interfaz principal para "volar" el vehículo.

Un ejemplo de un INS popular para aviones comerciales fue el Delco Carousel , que proporcionó una automatización parcial de la navegación en los días anteriores a que los sistemas completos de gestión de vuelo se volvieran comunes. El Carousel permitía a los pilotos ingresar 9 puntos de referencia a la vez y luego guiar la aeronave de un punto de referencia al siguiente utilizando un INS para determinar la posición y la velocidad de la aeronave. Boeing Corporation subcontrató a la División de Electrónica Delco de General Motors para diseñar y construir los primeros sistemas Carousel de producción para los primeros modelos (-100, -200 y -300) del avión 747. El 747 utilizó tres sistemas Carousel que operaban en conjunto para fines de confiabilidad. El sistema Carousel y sus derivados se adoptaron posteriormente para su uso en muchos otros aviones comerciales y militares. El C-141 de la USAF fue el primer avión militar en utilizar el Carousel en una configuración de sistema dual, seguido por el C-5A que utilizó la configuración triple INS, similar al 747. La flota KC-135A estaba equipada con un solo sistema Carousel IV-E que podía funcionar como un INS independiente o podía ser asistido por el radar Doppler AN/APN-81 o AN/APN-218 . Algunas variantes de misión especial del C-135 estaban equipadas con INS Carousel IV-E duales. La característica 704 de ARINC define el INS utilizado en el transporte aéreo comercial.

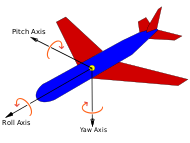
Los INS contienen unidades de medición inercial (IMU) que tienen acelerómetros angulares y lineales (para cambios de posición); algunas IMU incluyen un elemento giroscópico (para mantener una referencia angular absoluta).

Los acelerómetros angulares miden la rotación del vehículo en el espacio. Generalmente, hay al menos un sensor para cada uno de los tres ejes: cabeceo (morro hacia arriba y hacia abajo), guiñada (morro hacia la izquierda y hacia la derecha) y balanceo (en el sentido de las agujas del reloj o en sentido contrario a las agujas del reloj desde la cabina).

Los acelerómetros lineales miden las aceleraciones no gravitacionales ^[22] del vehículo. Dado que puede moverse en tres ejes (arriba y abajo, izquierda y derecha, adelante y atrás), hay un acelerómetro lineal para cada eje.

Una computadora calcula continuamente la posición actual del vehículo. Primero, para cada uno de los seis grados de libertad (x, y, z y θ _x , θ _y y θ _z ), integra a lo largo del tiempo la aceleración detectada, junto con una estimación de la gravedad, para calcular la velocidad actual. Luego integra la velocidad para calcular la posición actual.

La guía inercial es difícil sin computadoras. El deseo de utilizar guía inercial en el misil Minuteman y el Proyecto Apolo impulsó los primeros intentos de miniaturizar las computadoras.

En la actualidad, los sistemas de guiado inercial suelen combinarse con sistemas de navegación por satélite mediante un sistema de filtrado digital. El sistema inercial proporciona datos a corto plazo, mientras que el sistema por satélite corrige los errores acumulados del sistema inercial.

Un sistema de guía inercial que operará cerca de la superficie de la Tierra debe incorporar un ajuste Schuler para que su plataforma continúe apuntando hacia el centro de la Tierra a medida que un vehículo se mueve de un lugar a otro.

Algunos sistemas colocan los acelerómetros lineales sobre una plataforma giroestabilizada con cardán. Los cardanes son un conjunto de tres anillos, cada uno con un par de cojinetes inicialmente en ángulo recto. Permiten que la plataforma gire sobre cualquier eje de rotación (o, más bien, permiten que la plataforma mantenga la misma orientación mientras el vehículo gira alrededor de ella). Hay dos giroscopios (normalmente) en la plataforma.

Se utilizan dos giroscopios para cancelar la precesión giroscópica , la tendencia de un giroscopio a girar en ángulo recto con respecto a un par de entrada. Al montar un par de giroscopios (con la misma inercia rotacional y girando a la misma velocidad en direcciones opuestas) en ángulo recto, se cancelan las precesiones y la plataforma resistirá la torsión. ^{[ cita requerida ]}

Este sistema permite medir los ángulos de balanceo, cabeceo y guiñada de un vehículo directamente en los cojinetes de los cardanes. Se pueden utilizar circuitos electrónicos relativamente simples para sumar las aceleraciones lineales, ya que las direcciones de los acelerómetros lineales no cambian.

La gran desventaja de este esquema es que utiliza muchas piezas mecánicas de precisión costosas. También tiene partes móviles que pueden desgastarse o atascarse y es vulnerable al bloqueo del cardán . El sistema de guía principal de la nave espacial Apolo utilizaba una plataforma giroestabilizada de tres ejes, que alimentaba datos a la computadora de guía Apolo . Las maniobras debían planificarse cuidadosamente para evitar el bloqueo del cardán.

El bloqueo del cardán limita las maniobras y sería beneficioso eliminar los anillos colectores y los cojinetes de los cardanes. Por lo tanto, algunos sistemas utilizan cojinetes de fluido o una cámara de flotación para montar una plataforma giroestabilizada. Estos sistemas pueden tener precisiones muy altas (por ejemplo, Advanced Inertial Reference Sphere ). Como todas las plataformas giroestabilizadas, este sistema funciona bien con computadoras relativamente lentas y de bajo consumo.

Los cojinetes de fluido son almohadillas con orificios a través de los cuales se presiona gas inerte presurizado (como helio) o aceite contra la carcasa esférica de la plataforma. Los cojinetes de fluido son muy resbaladizos y la plataforma esférica puede girar libremente. Normalmente hay cuatro almohadillas de cojinete, montadas en una disposición tetraédrica para sostener la plataforma.

En los sistemas premium, los sensores angulares suelen ser bobinas de transformador especializadas fabricadas en una tira sobre una placa de circuito impreso flexible . Varias tiras de bobinas están montadas en círculos máximos alrededor de la carcasa esférica de la plataforma giroestabilizada. La electrónica fuera de la plataforma utiliza transformadores similares en forma de tira para leer los campos magnéticos variables producidos por los transformadores envueltos alrededor de la plataforma esférica. Siempre que un campo magnético cambia de forma o se mueve, cortará los cables de las bobinas en las tiras externas del transformador. El corte genera una corriente eléctrica en las bobinas externas en forma de tira y la electrónica puede medir esa corriente para derivar ángulos.

Los sistemas baratos a veces utilizan códigos de barras para detectar las orientaciones y utilizan células solares o un solo transformador para alimentar la plataforma. Algunos misiles pequeños han alimentado la plataforma con luz procedente de una ventana o fibras ópticas que llegan al motor. Un tema de investigación es suspender la plataforma con presión de los gases de escape. Los datos se devuelven al mundo exterior a través de los transformadores o, a veces, de los LED que se comunican con fotodiodos externos .

Las computadoras digitales livianas permiten que el sistema elimine los cardanes, creando sistemas de sujeción , llamados así porque sus sensores simplemente se sujetan al vehículo. Esto reduce el costo, elimina el bloqueo del cardán , elimina la necesidad de algunas calibraciones y aumenta la confiabilidad al eliminar algunas de las partes móviles. Los sensores de velocidad angular llamados giroscopios de velocidad miden la velocidad angular del vehículo.

Un sistema con correas necesita un rango de medición dinámico varios cientos de veces superior al requerido por un sistema con cardán. Es decir, debe integrar los cambios de actitud del vehículo en cabeceo, balanceo y guiñada, así como los movimientos generales. Los sistemas con cardán normalmente pueden funcionar bien con tasas de actualización de 50-60 Hz. Sin embargo, los sistemas con correas normalmente se actualizan alrededor de 2000 Hz. Se necesita una tasa más alta para permitir que el sistema de navegación integre la tasa angular en una actitud con precisión.

Los algoritmos de actualización de datos ( coseno de dirección o cuaterniones ) implicados son demasiado complejos para ser realizados con precisión, salvo por la electrónica digital. Sin embargo, las computadoras digitales son ahora tan económicas y rápidas que los sistemas de giroscopios de velocidad pueden utilizarse en la práctica y producirse en masa. El módulo lunar Apolo utilizó un sistema de sujeción en su sistema de guía de aborto (AGS) de respaldo .

Los sistemas strapdown se utilizan hoy en día en aplicaciones comerciales y militares (aeronaves, barcos, vehículos teledirigidos , misiles , etc.). Los sistemas strapdown de última generación se basan en giroscopios láser de anillo , giroscopios de fibra óptica o giroscopios de resonador hemisférico . Utilizan electrónica digital y técnicas avanzadas de filtrado digital, como el filtro Kalman .

La orientación de un sistema de giroscopio también puede inferirse a veces simplemente a partir de su historial de posición (por ejemplo, GPS). Este es el caso, en particular, de los aviones y los automóviles, donde el vector de velocidad suele implicar la orientación de la carrocería del vehículo.

Por ejemplo, el proceso de inicialización Align in Motion ^[23] de Honeywell se realiza mientras la aeronave está en movimiento, en el aire o en tierra. Esto se logra utilizando GPS y una prueba de razonabilidad inercial, lo que permite cumplir con los requisitos de integridad de datos comerciales. Este proceso ha sido certificado por la FAA para recuperar un rendimiento INS puro equivalente a los procedimientos de alineación estacionaria para tiempos de vuelo civiles de hasta 18 horas. Evita la necesidad de baterías de giroscopio en las aeronaves.

Los sistemas de navegación menos costosos, destinados a su uso en automóviles, pueden utilizar un giroscopio de estructura vibratoria para detectar cambios en el rumbo y el captador del odómetro para medir la distancia recorrida a lo largo de la trayectoria del vehículo. Este tipo de sistema es mucho menos preciso que un INS de gama alta, pero es adecuado para la aplicación típica de automóviles donde el GPS es el sistema de navegación principal y la estimación de la posición solo se necesita para llenar los vacíos en la cobertura del GPS cuando los edificios o el terreno bloquean las señales satelitales.

Si se induce una onda estacionaria en una estructura resonante hemisférica y luego se hace girar dicha estructura, la onda estacionaria armónica esférica gira en un ángulo diferente al de la estructura del resonador de cuarzo debido a la fuerza de Coriolis. El movimiento de la carcasa exterior con respecto al patrón de onda estacionaria es proporcional al ángulo de rotación total y puede detectarse mediante la electrónica adecuada. Los resonadores del sistema están fabricados a partir de cuarzo fundido debido a sus excelentes propiedades mecánicas. Los electrodos que impulsan y detectan las ondas estacionarias se depositan directamente sobre estructuras de cuarzo separadas que rodean al resonador. Estos giroscopios pueden funcionar en modo de ángulo completo (lo que les da una capacidad de velocidad casi ilimitada) o en modo de reequilibrio de fuerza que mantiene la onda estacionaria en una orientación fija con respecto a la carcasa del giroscopio (lo que les da una precisión mucho mejor).

Este sistema casi no tiene partes móviles y es muy preciso. Sin embargo, sigue siendo relativamente caro debido al costo de los hemisferios huecos de cuarzo pulidos y esmerilados con precisión. Northrop Grumman fabrica actualmente IMU ( unidades de medición inercial ) para naves espaciales que utilizan HRG. Estas IMU han demostrado una confiabilidad extremadamente alta desde su uso inicial en 1996. ^[24] Safran fabrica una gran cantidad de sistemas de navegación inercial basados ​​en HRG dedicados a una amplia gama de aplicaciones. ^[25]

This section needs to be updated. Please help update this article to reflect recent events or newly available information. (October 2018)

Entre estos productos se encuentran los "giroscopios de diapasón", que están diseñados como diapasones accionados electrónicamente y que suelen estar fabricados a partir de una única pieza de cuarzo o silicio. Estos giroscopios funcionan de acuerdo con la teoría dinámica según la cual, cuando se aplica una velocidad angular a un cuerpo que se desplaza, se genera una fuerza de Coriolis .

Este sistema suele estar integrado en un chip de silicio. Tiene dos diapasones de cuarzo con masa equilibrada, dispuestos "mango con mango" de modo que las fuerzas se cancelan. Los electrodos de aluminio evaporados sobre los diapasones y el chip subyacente impulsan y detectan el movimiento. El sistema se puede fabricar y es económico. Dado que el cuarzo es dimensionalmente estable, el sistema puede ser preciso.

A medida que las horquillas giran alrededor del eje del mango, la vibración de las púas tiende a continuar en el mismo plano de movimiento. Este movimiento debe ser resistido por fuerzas electrostáticas de los electrodos que se encuentran debajo de las púas. Al medir la diferencia de capacitancia entre las dos púas de una horquilla, el sistema puede determinar la velocidad del movimiento angular.

La tecnología no militar de última generación (a fecha de 2005 ^[update]) permite construir pequeños sensores de estado sólido que pueden medir los movimientos del cuerpo humano. Estos dispositivos no tienen partes móviles y pesan unos 50 gramos (2 onzas).

Para la estabilización de imágenes en cámaras o videocámaras pequeñas se utilizan dispositivos de estado sólido que utilizan los mismos principios físicos . Estos pueden ser extremadamente pequeños, de alrededor de 5 milímetros (0,20 pulgadas) y están construidos con tecnologías de sistemas microelectromecánicos (MEMS). ^[26]

Se pueden utilizar sensores basados ​​en principios magnetohidrodinámicos para medir velocidades angulares.

Los giroscopios MEMS suelen basarse en el efecto Coriolis para medir la velocidad angular. Consisten en una masa de prueba resonante montada en silicio. El giroscopio es, a diferencia de un acelerómetro, un sensor activo. La masa de prueba es empujada hacia adelante y hacia atrás por peines de accionamiento. Una rotación del giroscopio genera una fuerza de Coriolis que actúa sobre la masa, lo que da como resultado un movimiento en una dirección diferente. El movimiento en esta dirección se mide mediante electrodos y representa la velocidad de giro. ^[27]

Un giroscopio láser de anillo (RLG) divide un haz de luz láser en dos haces en direcciones opuestas a través de túneles estrechos en un camino óptico circular cerrado alrededor del perímetro de un bloque triangular de vidrio Cervit estable a la temperatura con espejos reflectantes colocados en cada esquina. Cuando el giroscopio gira a una cierta velocidad angular, la distancia recorrida por cada haz será diferente, siendo el camino más corto opuesto a la rotación. El cambio de fase entre los dos haces se puede medir con un interferómetro y es proporcional a la velocidad de rotación ( efecto Sagnac ).

En la práctica, a bajas velocidades de rotación, la frecuencia de salida puede caer a cero como resultado de la retrodispersión, que hace que los haces se sincronicen y se bloqueen entre sí. Esto se conoce como bloqueo o bloqueo láser . El resultado es que no hay cambios en el patrón de interferencia y, por lo tanto, no hay cambios en la medición.

Para desbloquear los rayos de luz contrarrotativos, los giroscopios láser tienen trayectorias de luz independientes para las dos direcciones (generalmente en giroscopios de fibra óptica) o el giroscopio láser está montado en un motor piezoeléctrico que hace vibrar rápidamente el anillo láser hacia adelante y hacia atrás sobre su eje de entrada a través de la región de bloqueo para desacoplar las ondas de luz.

El vibrador es el más preciso, porque ambos rayos de luz siguen exactamente el mismo camino. Por lo tanto, los giroscopios láser conservan partes móviles, pero no se mueven tan lejos.

Una variación más reciente del giroscopio óptico, el giroscopio de fibra óptica (FOG), utiliza un láser externo y dos haces que van en direcciones opuestas (contrapropagación) en carretes largos (de varios kilómetros) de filamento de fibra óptica, comparándose la diferencia de fase de los dos haces después de su viaje a través de los carretes de fibra.

El mecanismo básico, la luz láser monocromática que viaja en trayectorias opuestas y el efecto Sagnac , es el mismo en un FOG y un RLG, pero los detalles de ingeniería son sustancialmente diferentes en el FOG en comparación con los giroscopios láser anteriores.

Se requiere un bobinado preciso de la bobina de fibra óptica para garantizar que las trayectorias que toma la luz en direcciones opuestas sean lo más similares posibles. El FOG requiere calibraciones más complejas que un giroscopio de anillo láser, lo que hace que el desarrollo y la fabricación de FOG sean más desafiantes técnicamente que para un RLG. Sin embargo, los FOG no sufren bloqueos láser a bajas velocidades y no necesitan contener partes móviles, lo que aumenta la precisión potencial máxima y la vida útil de un FOG en comparación con un RLG equivalente.

El acelerómetro básico de circuito abierto consta de una masa unida a un resorte. La masa está limitada a moverse solo en línea con el resorte. La aceleración provoca la deflexión de la masa y se mide la distancia de desplazamiento. La aceleración se deriva de los valores de la distancia de deflexión, la masa y la constante del resorte. El sistema también debe amortiguarse para evitar la oscilación. Un acelerómetro de circuito cerrado logra un mayor rendimiento al utilizar un bucle de retroalimentación para cancelar la deflexión, manteniendo así la masa casi estacionaria. Siempre que la masa se desvía, el bucle de retroalimentación hace que una bobina eléctrica aplique una fuerza igualmente negativa sobre la masa, cancelando el movimiento. La aceleración se deriva de la cantidad de fuerza negativa aplicada. Debido a que la masa apenas se mueve, los efectos de las no linealidades del resorte y el sistema de amortiguación se reducen en gran medida. Además, este acelerómetro proporciona un mayor ancho de banda más allá de la frecuencia natural del elemento sensor.

Ambos tipos de acelerómetros se han fabricado como micromaquinaria integrada en chips de silicio.

El departamento de la Oficina de Tecnología de Microsistemas (MTO) de DARPA está trabajando en un programa Micro-PNT (Microtecnología para Posicionamiento, Navegación y Temporización) para diseñar chips de Unidad de Medición Inercial y de Temporización (TIMU) que realicen un seguimiento de la posición absoluta en un solo chip sin navegación asistida por GPS. ^{[28] [29] [30]}

Micro-PNT agrega un reloj de sincronización maestro de alta precisión ^[31] integrado en un chip IMU (Unidad de medición inercial), lo que lo convierte en un chip de unidad de medición inercial y de sincronización. Un chip TIMU integra un giroscopio de 3 ejes, un acelerómetro de 3 ejes y un magnetómetro de 3 ejes junto con un reloj de sincronización maestro de alta precisión, de modo que puede medir simultáneamente el movimiento rastreado y combinarlo con la sincronización del reloj sincronizado. ^{[28] [29]}

En una forma, el sistema de ecuaciones de navegación adquiere medidas lineales y angulares del marco inercial y del cuerpo, respectivamente, y calcula la actitud y posición finales en el marco de referencia NED .

Donde f es la fuerza específica, a es la velocidad angular, a es la aceleración, R es la posición y V es la velocidad, g es la aceleración debida a la gravedad y h son los parámetros de ubicación NED. Además, los superíndices/subíndices de E, I y B representan variables en el marco de referencia centrado en la Tierra, inercial o corporal, respectivamente, y C es una transformación de los marcos de referencia. ^{[ cita requerida ]}${\displaystyle \omega }$${\displaystyle {\dot {R}}}$${\displaystyle \Omega }$${\displaystyle \Phi ,\lambda }$

• Índice de artículos sobre aviación
• Control de actitud de naves espaciales  : proceso de control de la orientación de un vehículo aeroespacial
• Sistema de navegación inercial LN-3

• Zanetti, Renato; d'Souza, Christopher (2020), "Navegación inercial", Enciclopedia de sistemas y control , págs. 1–7, doi :10.1007/978-1-4471-5102-9_100036-1, ISBN 978-1-4471-5102-9
• AD King (1998). "Navegación inercial: cuarenta años de evolución" (PDF) . GEC Review . 13 (3). General Electric Company plc : 140–149.
• E. v. Hinueber (iMAR Navigation) (2011). "Diseño de un sistema de referencia de actitud de aeronave sin ayuda con giroscopios de precisión media para requisitos de actitud de alto rendimiento". Inertial Sensors and Systems, Symposium Gyro Technology, Karlsruhe / Alemania . 2011. iMAR Navigation / DGON.

• Sistema de Navegación Inercial Ferranti (INAS)
• Sistema de navegación inercial
• Principio de funcionamiento de un acelerómetro
• Descripción general de los tipos de instrumentos inerciales
• Guía de navegación inercial de Oxford Technical Solutions
• Listado de sistemas de navegación inercial de código abierto
• Impacto de los errores de los sensores inerciales en los errores de posición y actitud del sistema de navegación inercial
• Introducción a los sistemas de navegación inercial en aplicaciones UAV/drones