Reconstrucción 3D

Este artículo necesita ser actualizado . Por favor, ayude a actualizar este artículo para reflejar eventos recientes o nueva información disponible. ( Octubre de 2019 )

En visión artificial y gráficos por computadora , la reconstrucción 3D es el proceso de capturar la forma y apariencia de objetos reales. Este proceso puede llevarse a cabo mediante métodos activos o pasivos. ^[1] Si se permite que el modelo cambie su forma en el tiempo, esto se conoce como reconstrucción no rígida o espacio-temporal . ^[2]

La investigación de la reconstrucción 3D siempre ha sido un objetivo difícil. Mediante el uso de la reconstrucción 3D se puede determinar el perfil 3D de cualquier objeto, así como conocer la coordenada 3D de cualquier punto del perfil. La reconstrucción 3D de objetos es un problema generalmente científico y una tecnología central de una amplia variedad de campos, como el diseño geométrico asistido por computadora ( CAGD ), los gráficos por computadora , la animación por computadora , la visión por computadora , las imágenes médicas , la ciencia computacional , la realidad virtual , los medios digitales , etc. ^[3] Por ejemplo, la información de las lesiones de los pacientes se puede presentar en 3D en la computadora, lo que ofrece un enfoque nuevo y preciso en el diagnóstico y, por lo tanto, tiene un valor clínico vital. ^[4] Los modelos de elevación digitales se pueden reconstruir utilizando métodos como la altimetría láser aerotransportada ^[5] o el radar de apertura sintética . ^[6]

Los métodos activos, es decir, los métodos de datos de rango, dado el mapa de profundidad , reconstruyen el perfil 3D mediante un enfoque de aproximación numérica y construyen el objeto en un escenario basado en el modelo. Estos métodos interfieren activamente con el objeto reconstruido, ya sea mecánicamente o radiométricamente utilizando telémetros , para adquirir el mapa de profundidad, por ejemplo, luz estructurada , telémetro láser y otras técnicas de detección activa. Un ejemplo simple de un método mecánico utilizaría un medidor de profundidad para medir una distancia a un objeto giratorio colocado en una plataforma giratoria. Los métodos radiométricos más aplicables emiten radiancia hacia el objeto y luego miden su parte reflejada. Los ejemplos van desde fuentes de luz en movimiento, luz visible coloreada, láseres de tiempo de vuelo ^[7] hasta microondas o ultrasonido 3D . Consulte escaneo 3D para obtener más detalles.

Los métodos pasivos de reconstrucción 3D no interfieren con el objeto reconstruido; solo utilizan un sensor para medir la radiancia reflejada o emitida por la superficie del objeto para inferir su estructura 3D a través de la comprensión de la imagen . ^[8] Normalmente, el sensor es un sensor de imagen en una cámara sensible a la luz visible y la entrada al método es un conjunto de imágenes digitales (una, dos o más) o vídeo. En este caso hablamos de reconstrucción basada en imágenes y la salida es un modelo 3D . En comparación con los métodos activos, los métodos pasivos se pueden aplicar a una gama más amplia de situaciones. ^[9]

Los métodos de señales monoculares se refieren al uso de una o más imágenes desde un punto de vista (cámara) para proceder a la construcción 3D. Hace uso de características 2D (por ejemplo, siluetas, sombreado y textura) para medir la forma 3D, y es por eso que también se denomina Forma-a-partir-de-X, donde X puede ser siluetas , sombreado , textura, etc. La reconstrucción 3D a través de señales monoculares es simple y rápida, y solo se necesita una imagen digital apropiada, por lo que solo una cámara es adecuada. Técnicamente, evita la correspondencia estéreo , que es bastante compleja. ^[10]

Forma a partir del sombreado Debido al análisis de la información de sombra en la imagen, mediante el uso de la reflectancia lambertiana , se restaura la profundidad de la información normal de la superficie del objeto para reconstruirlo. ^[12]

Estereofotometría Este enfoque es más sofisticado que el método de la forma del sombreado. Se utilizan imágenes tomadas en diferentes condiciones de iluminación para resolver la información de profundidad. Vale la pena mencionar que este enfoque requiere más de una imagen. ^[13]

Forma a partir de textura Supongamos que un objeto tiene una superficie lisa cubierta por unidades de textura replicadas y su proyección de 3D a 2D provoca distorsión y perspectiva . La distorsión y la perspectiva medidas en imágenes 2D proporcionan la pista para resolver de manera inversa la profundidad de la información normal de la superficie del objeto. ^[14]

Soluciones basadas en aprendizaje automático El aprendizaje automático permite aprender la correspondencia entre las características sutiles en la entrada y el equivalente 3D respectivo. Las redes neuronales profundas han demostrado ser muy eficaces para la reconstrucción 3D a partir de una imagen de un solo color. ^[15] Esto funciona incluso para imágenes de entrada no fotorrealistas, como bocetos. ^[16] Gracias al alto nivel de precisión en las características 3D reconstruidas, el método basado en aprendizaje profundo se ha empleado para aplicaciones de ingeniería biomédica para reconstruir imágenes de TC a partir de rayos X. ^[17]

Se ha sugerido que esta sección se divida en otro artículo titulado Visión estereoscópica por computadora . ( Discutir ) (octubre de 2021)

La visión estereoscópica obtiene la información geométrica tridimensional de un objeto a partir de múltiples imágenes basándose en la investigación del sistema visual humano . ^[18] Los resultados se presentan en forma de mapas de profundidad. Las imágenes de un objeto adquiridas por dos cámaras simultáneamente en diferentes ángulos de visión , o por una sola cámara en diferentes momentos en diferentes ángulos de visión, se utilizan para restaurar su información geométrica tridimensional y reconstruir su perfil y ubicación tridimensionales. Esto es más directo que los métodos monoculares como la forma a partir del sombreado.

El método de visión estereoscópica binocular requiere dos cámaras idénticas con ejes ópticos paralelos para observar un mismo objeto y obtener dos imágenes desde diferentes puntos de vista. En términos de relaciones trigonométricas, la información de profundidad se puede calcular a partir de la disparidad. El método de visión estereoscópica binocular está bien desarrollado y contribuye de manera estable a una reconstrucción 3D favorable, lo que conduce a un mejor rendimiento en comparación con otras construcciones 3D. Desafortunadamente, requiere un gran esfuerzo computacional y, además, su rendimiento es bastante deficiente cuando la distancia de referencia es grande.

El enfoque de utilizar la visión estéreo binocular para adquirir información geométrica 3D de los objetos se basa en la disparidad visual . ^[19] La siguiente imagen proporciona un diagrama esquemático simple de la visión estéreo binocular con visión horizontal, donde b es la línea de base entre los centros proyectivos de dos cámaras.

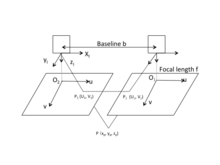
El origen del sistema de coordenadas de la cámara está en el centro óptico de la lente de la cámara, como se muestra en la figura. En realidad, el plano de imagen de la cámara está detrás del centro óptico de la lente de la cámara. Sin embargo, para simplificar el cálculo, las imágenes se dibujan delante del centro óptico de la lente mediante f. El eje u y el eje v del sistema de coordenadas de la imagen están en la misma dirección que el eje x y el eje y del sistema de coordenadas de la cámara, respectivamente. El origen del sistema de coordenadas de la imagen se encuentra en la intersección del plano de imagen y el eje óptico. Supongamos que existe un punto del mundo cuyos puntos de imagen correspondientes están y respectivamente en el plano de imagen izquierdo y derecho. Supongamos que dos cámaras están en el mismo plano, entonces las coordenadas y de y son idénticas, es decir, . Según las relaciones trigonométricas ,$Estilo de visualización O_{1}uv$${\estilo de visualización P}$${\ Displaystyle P_ {1} (u_ {1}, v_ {1})}$${\ Displaystyle P_ {2} (u_ {2}, v_ {2})}$$Estilo de visualización P_{1}$$Estilo de visualización P_{2}$${\displaystyle v_{1}=v_{2}}$

${\displaystyle u_{1}=f{\frac {x_{p}}{z_{p}}}}$

${\displaystyle u_{2}=f{\frac {x_{p}-b}{z_{p}}}}$

${\displaystyle v_{1}=v_{2}=f{\frac {y_{p}}{z_{p}}}}$

donde son las coordenadas de en el sistema de coordenadas de la cámara izquierda, es la distancia focal de la cámara. La disparidad visual se define como la diferencia en la ubicación del punto de imagen de un cierto punto del mundo adquirido por dos cámaras,${\ Displaystyle (x_ {p}, y_ {p}, z_ {p})}$${\estilo de visualización P}$${\estilo de visualización f}$

${\displaystyle d=u_{1}-u_{2}=f{\frac {b}{z_{p}}}}$

en base a lo cual se pueden calcular las coordenadas de .${\estilo de visualización P}$

Por lo tanto, una vez conocidas las coordenadas de los puntos de la imagen, además de los parámetros de dos cámaras, se puede determinar la coordenada 3D del punto.

${\displaystyle x_{p}={\frac {bu_{1}}{d}}}$

${\displaystyle y_{p}={\frac {bv_{1}}{d}}}$

${\displaystyle z_{p}={\frac {bf}{d}}}$

La reconstrucción 3D consta de las siguientes secciones:

La adquisición de imágenes digitales 2D es la fuente de información de la reconstrucción 3D. La reconstrucción 3D que se utiliza habitualmente se basa en dos o más imágenes, aunque en algunos casos puede emplear solo una imagen. Existen varios tipos de métodos para la adquisición de imágenes que dependen de las ocasiones y los propósitos de la aplicación específica. No solo se deben cumplir los requisitos de la aplicación, sino que también se deben considerar la disparidad visual, la iluminación, el rendimiento de la cámara y las características del escenario.

La calibración de la cámara en la visión estereoscópica binocular se refiere a la determinación de la relación de mapeo entre los puntos de la imagen y las coordenadas espaciales en el escenario 3D. La calibración de la cámara es una parte básica y esencial en la reconstrucción 3D mediante la visión estereoscópica binocular.${\ Displaystyle P_ {1} (u_ {1}, v_ {1})}$${\ Displaystyle P_ {2} (u_ {2}, v_ {2})}$${\ Displaystyle P (x_ {p}, y_ {p}, z_ {p})}$

El objetivo de la extracción de características es obtener las características de las imágenes, a través de las cuales se procesa la correspondencia estereoscópica. Como resultado, las características de las imágenes están estrechamente vinculadas a la elección de los métodos de comparación. No existe una teoría de aplicación universal para la extracción de características, lo que conduce a una gran diversidad de correspondencias estereoscópicas en la investigación de la visión estereoscópica binocular.

La correspondencia estéreo consiste en establecer la correspondencia entre factores primitivos en imágenes, es decir, hacer coincidir y a partir de dos imágenes. Se deben tener en cuenta ciertos factores de interferencia en el escenario, por ejemplo, iluminación, ruido, características físicas de la superficie, etc.${\ Displaystyle P_ {1} (u_ {1}, v_ {1})}$${\ Displaystyle P_ {2} (u_ {2}, v_ {2})}$

De acuerdo con la correspondencia precisa, combinada con los parámetros de ubicación de la cámara, se puede recuperar información geométrica 3D sin dificultades. Debido a que la precisión de la reconstrucción 3D depende de la precisión de la correspondencia, el error de los parámetros de ubicación de la cámara, etc., los procedimientos anteriores deben realizarse con cuidado para lograr una reconstrucción 3D relativamente precisa.

La rutina clínica de diagnóstico, el seguimiento del paciente, la cirugía asistida por computadora, la planificación quirúrgica, etc. se facilitan con modelos 3D precisos de la parte deseada de la anatomía humana. La motivación principal detrás de la reconstrucción 3D incluye

• Precisión mejorada gracias a la agregación de múltiples vistas.
• Estimaciones de superficie detalladas.
• Se puede utilizar para planificar, simular, guiar o ayudar de otro modo a un cirujano a realizar un procedimiento médico.
• Se puede determinar la posición y orientación precisas de la anatomía del paciente.
• Ayuda en diversas áreas clínicas, como planificación de radioterapia y verificación del tratamiento, cirugía de columna, reemplazo de cadera, neurointervenciones y colocación de stents aórticos.

Aplicaciones:

La reconstrucción 3D tiene aplicaciones en muchos campos, entre ellos:

• Ingeniería de pavimentos ^{[7] [20]}
• Medicina ^[4]
• Reconstrucción de vídeo desde un punto de vista libre ^[21]
• Mapeo robótico ^[22]
• Planificación urbana ^[23]
• Reconstrucción tomográfica ^[24]
• Juegos ^[25]
• Entornos virtuales y turismo virtual ^[25]
• Observación de la Tierra
• Arqueología ^[26]
• Realidad aumentada ^[27]
• Ingeniería inversa ^[28]
• Captura de movimiento ^[29]
• Reconocimiento de objetos 3D , ^[30] reconocimiento de gestos y seguimiento de manos ^[31]

Planteamiento del problema:

La mayoría de los algoritmos disponibles para la reconstrucción 3D son extremadamente lentos y no se pueden utilizar en tiempo real. Aunque los algoritmos presentados aún están en sus primeras etapas, tienen potencial para realizar cálculos rápidos.

Enfoques existentes:

Delaunay y las formas alfa

• El método de Delaunay implica la extracción de superficies tetraédricas a partir de una nube de puntos inicial. La idea de "forma" para un conjunto de puntos en el espacio viene dada por el concepto de formas alfa. Dado un conjunto finito de puntos S y el parámetro real alfa, la forma alfa de S es un politopo (la generalización a cualquier dimensión de un polígono bidimensional y un poliedro tridimensional) que no es convexo ni necesariamente conectado. ^[32] Para un valor grande, la forma alfa es idéntica a la envoltura convexa de S. El algoritmo propuesto por Edelsbrunner y Mucke ^[33] elimina todos los tetraedros que están delimitados por una esfera circundante más pequeña que α. La superficie se obtiene entonces con los triángulos externos del tetraedro resultante. ^[33]
• Otro algoritmo llamado Tight Cocone ^[34] etiqueta los tetraedros iniciales como interiores y exteriores. Los triángulos que se encuentran dentro y fuera generan la superficie resultante.

Ambos métodos se han ampliado recientemente para reconstruir nubes de puntos con ruido. ^[34] En este método, la calidad de los puntos determina la viabilidad del método. Para una triangulación precisa, dado que utilizamos todo el conjunto de nubes de puntos, los puntos de la superficie con un error superior al umbral se representarán explícitamente en la geometría reconstruida. ^[32]

Métodos de puesta a cero

La reconstrucción de la superficie se realiza utilizando una función de distancia que asigna a cada punto en el espacio una distancia con signo a la superficie S . Se utiliza un algoritmo de contorno para extraer un conjunto de ceros que se utiliza para obtener la representación poligonal del objeto. Por lo tanto, el problema de reconstruir una superficie a partir de una nube de puntos desorganizada se reduce a la definición de la función apropiada f con un valor cero para los puntos muestreados y diferente al valor cero para el resto. Un algoritmo llamado cubos de marcha estableció el uso de tales métodos. ^[35] Hay diferentes variantes para un algoritmo dado, algunas utilizan una función discreta f , mientras que otras utilizan una función de base radial poliarmónica que se utiliza para ajustar el conjunto de puntos inicial. ^{[36] [37]} También se han utilizado funciones como Mínimos Cuadrados Móviles, funciones básicas con soporte local, ^[38] basadas en la ecuación de Poisson. La pérdida de la precisión de la geometría en áreas con curvatura extrema, es decir, esquinas, bordes es uno de los principales problemas encontrados. Además, el pretratamiento de la información, mediante la aplicación de algún tipo de técnica de filtrado, también afecta a la definición de las esquinas suavizándolas. Existen varios estudios relacionados con las técnicas de postprocesamiento utilizadas en la reconstrucción para la detección y refinamiento de esquinas pero estos métodos incrementan la complejidad de la solución. ^[39]

Técnica de realidad virtual

La transparencia total del volumen del objeto se visualiza mediante la técnica de realidad virtual. Las imágenes se obtienen proyectando rayos a través de los datos de volumen. A lo largo de cada rayo, se debe calcular la opacidad y el color en cada vóxel. Luego, la información calculada a lo largo de cada rayo se agregará a un píxel en el plano de la imagen. Esta técnica nos ayuda a ver de manera integral una estructura compacta completa del objeto. Dado que la técnica requiere una enorme cantidad de cálculos, lo que requiere computadoras de configuración sólida, es adecuada para datos de bajo contraste. Se pueden considerar dos métodos principales para la proyección de rayos, a saber:

• Método de orden de objetos: los rayos proyectados atraviesan el volumen de atrás hacia adelante (desde el volumen hasta el plano de la imagen).
• Método de proyección de rayos o de orden de imagen: los rayos proyectados atraviesan el volumen de adelante hacia atrás (desde el plano de la imagen hasta el volumen). Existen otros métodos para componer imágenes, métodos apropiados según los propósitos del usuario. Algunos métodos habituales en imágenes médicas son MIP (proyección de máxima intensidad), MinIP (proyección de mínima intensidad), AC ( composición alfa ) y NPVR ( representación de volumen no fotorrealista ).

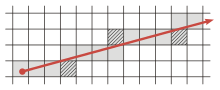
Cuadrícula de vóxeles

En esta técnica de filtrado se muestrea el espacio de entrada utilizando una rejilla de vóxeles 3D para reducir el número de puntos. ^[40] Para cada vóxel se elige un centroide como representante de todos los puntos. Existen dos enfoques, la selección del centroide del vóxel o la selección del centroide de los puntos que se encuentran dentro del vóxel. Obtener el promedio interno de puntos tiene un mayor coste computacional, pero ofrece mejores resultados. De esta forma, se obtiene un subconjunto del espacio de entrada que representa aproximadamente la superficie subyacente. El método de la rejilla de vóxeles presenta los mismos problemas que otras técnicas de filtrado: imposibilidad de definir el número final de puntos que representan la superficie, pérdida de información geométrica debido a la reducción de los puntos dentro de un vóxel y sensibilidad a espacios de entrada ruidosos.

• Modelado 3D
• Adquisición de datos 3D y reconstrucción de objetos
• Reconstrucción 3D a partir de múltiples imágenes
• Escáner 3D
• Reconstrucción de superficies mediante SEM 3D
• Reconstrucción 4D
• Mapa de profundidad
• Kinect
• Fotogrametría
• Estereoscopia
• Estructura a partir del movimiento

Busque reconstrucción 3D en Wikcionario, el diccionario libre.

• Sintetización de formas 3D mediante el modelado de siluetas y mapas de profundidad de múltiples vistas con redes generativas profundas: genere y reconstruya formas 3D mediante el modelado de siluetas o mapas de profundidad de múltiples vistas.

• http://www.nature.com/subjects/3d-reconstruction#news-and-comment
• http://6.869.csail.mit.edu/fa13/lectures/lecture11shapefromX.pdf
• http://research.microsoft.com/apps/search/default.aspx?q=3d+reconstruction
• https://research.google.com/search.html#q=3D%20reconstrucción