Ilustración del teorema del límite central
En teoría de la probabilidad, el teorema del límite central (TLC) establece que, en muchas situaciones, cuando se suman variables aleatorias independientes e idénticamente distribuidas, su suma correctamente normalizada tiende a una distribución normal. Este artículo ofrece dos ejemplos de este teorema. Ambos implican la suma de variables aleatorias independientes e idénticamente distribuidas y muestran cómo la distribución de probabilidad de la suma se acerca a la distribución normal a medida que aumenta el número de términos en la suma.
La primera ilustración implica una distribución de probabilidad continua , para la cual las variables aleatorias tienen una función de densidad de probabilidad . La segunda ilustración, para la cual la mayor parte del cálculo se puede hacer a mano, implica una distribución de probabilidad discreta , que se caracteriza por una función de masa de probabilidad .
Ilustración del caso continuo
La densidad de la suma de dos variables aleatorias independientes de valor real es igual a la convolución de las funciones de densidad de las variables originales.
Así, la densidad de la suma de m + n términos de una secuencia de variables independientes idénticamente distribuidas es igual a la convolución de las densidades de las sumas de m términos y de n términos. En particular, la densidad de la suma de n + 1 términos es igual a la convolución de la densidad de la suma de n términos con la densidad original (la "suma" de 1 término).
En la primera figura que figura a continuación se muestra una función de densidad de probabilidad . A continuación, en las siguientes figuras se muestran las densidades de las sumas de dos, tres y cuatro variables independientes distribuidas de forma idéntica , cada una con la densidad original. Si la densidad original es un polinomio por partes , como en el ejemplo, también lo son las densidades de las sumas, de grado cada vez mayor. Aunque la densidad original está lejos de ser normal, la densidad de la suma de unas pocas variables con esa densidad es mucho más suave y tiene algunas de las características cualitativas de la densidad normal .
Las convoluciones se calcularon mediante la transformada de Fourier discreta . Se construyó una lista de valores y = f ( x 0 + k Δ x ), donde f es la función de densidad original, Δ x es aproximadamente igual a 0,002 y k es igual a 0 a 1000. Se calculó la transformada de Fourier discreta Y de y . Luego, la convolución de f consigo misma es proporcional a la transformada de Fourier discreta inversa del producto puntual de Y consigo misma.
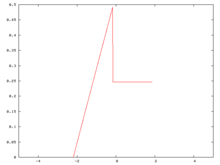
Función de densidad de probabilidad original
Empecemos con una función de densidad de probabilidad. Esta función, aunque discontinua, está lejos de ser el ejemplo más patológico que se podría crear. Se trata de un polinomio por partes, con partes de grados 0 y 1. La media de esta distribución es 0 y su desviación típica es 1.

Función de densidad de probabilidad de la suma de dos términos
A continuación, calculamos la densidad de la suma de dos variables independientes , cada una con la densidad anterior. La densidad de la suma es la convolución de la densidad anterior consigo misma.
La suma de dos variables tiene media 0. La densidad mostrada en la figura de la derecha ha sido reescalada por , de modo que su desviación estándar es 1.
Esta densidad ya es más suave que la original. Hay grumos evidentes que corresponden a los intervalos en los que se definió la densidad original.

Función de densidad de probabilidad de la suma de tres términos
Luego calculamos la densidad de la suma de tres variables independientes, cada una con la densidad anterior. La densidad de la suma es la convolución de la primera densidad con la segunda.
La suma de tres variables tiene media 0. La densidad mostrada en la figura de la derecha ha sido reescalada por √ 3 , de modo que su desviación estándar es 1.
Esta densidad es aún más suave que la anterior. En esta figura apenas se pueden detectar los grumos.

Función de densidad de probabilidad de la suma de cuatro términos
Por último, calculamos la densidad de la suma de cuatro variables independientes, cada una con la densidad indicada anteriormente. La densidad de la suma es la convolución de la primera densidad con la tercera (o de la segunda densidad consigo misma).
La suma de cuatro variables tiene media 0. La densidad mostrada en la figura de la derecha ha sido reescalada por √ 4 , de modo que su desviación estándar es 1.
Esta densidad parece cualitativamente muy similar a una densidad normal . No se pueden distinguir grumos a simple vista.
Ilustración del caso discreto
Esta sección ilustra el teorema del límite central mediante un ejemplo en el que el cálculo se puede realizar rápidamente a mano en papel, a diferencia del ejemplo que requiere un uso más intensivo de recursos informáticos de la sección anterior.

Función de masa de probabilidad original
Supongamos que la distribución de probabilidad de una variable aleatoria discreta X asigna pesos iguales a 1, 2 y 3:
La función de masa de probabilidad de la variable aleatoria X se puede representar mediante el siguiente gráfico de barras :
Es evidente que no se parece en nada a la curva en forma de campana de la distribución normal. Compare lo anterior con las representaciones que aparecen a continuación.

Función de masa de probabilidad de la suma de dos términos
Consideremos ahora la suma de dos copias independientes de X :
La función de masa de probabilidad de esta suma se puede representar así:
Esto todavía no se parece mucho a la curva en forma de campana, pero, al igual que la curva en forma de campana y a diferencia de la función de masa de probabilidad de X en sí, es más alta en el medio que en las dos colas.

Función de masa de probabilidad de la suma de tres términos
Ahora consideremos la suma de tres copias independientes de esta variable aleatoria:
La función de masa de probabilidad de esta suma se puede representar así:
No sólo es más grande en el centro que en las colas, sino que a medida que uno se mueve hacia el centro desde cualquiera de las colas, la pendiente primero aumenta y luego disminuye, tal como ocurre con la curva en forma de campana.
El grado de semejanza con la curva en forma de campana se puede cuantificar de la siguiente manera. Consideremos
- Pr( X 1 + X 2 + X 3 ≤ 7) = 1/27 + 3/27 + 6/27 + 7/27 + 6/27 = 23/27 = 0,85185... .
¿Qué tan cerca está esto de lo que daría una aproximación normal ? Se puede ver fácilmente que el valor esperado de Y = X 1 + X 2 + X 3 es 6 y la desviación estándar de Y es la raíz cuadrada de 2. Como Y ≤ 7 (desigualdad débil) si y solo si Y < 8 (desigualdad estricta), usamos una corrección de continuidad y buscamos
donde Z tiene una distribución normal estándar. La diferencia entre 0,85185... y 0,85558... parece notablemente pequeña si se considera que el número de variables aleatorias independientes que se agregaron fue solo tres.
Función de masa de probabilidad de la suma de 1.000 términos

La siguiente imagen muestra el resultado de una simulación basada en el ejemplo presentado en esta página. La extracción de la distribución uniforme se repite 1.000 veces y los resultados se suman.
Como la simulación se basa en el método de Monte Carlo , el proceso se repite 10.000 veces. Los resultados muestran que la distribución de la suma de 1.000 extracciones uniformes se asemeja mucho a la curva en forma de campana.
Enlaces externos
- Suma uniforme en Mathworld
- Ejemplos animados del CLT
- Actividad SOCR CLT de dinámica general
- Simulación interactiva del teorema del límite central para Windows
- La actividad SOCR CLT proporciona una demostración práctica de la teoría y las aplicaciones de este teorema de límite.
- Un vídeo musical que demuestra el teorema del límite central con un tablero de Galton por Carl McTague




