Funciones hiperbólicas inversas

En matemáticas , las funciones hiperbólicas inversas son inversas de las funciones hiperbólicas , análogas a las funciones circulares inversas . Hay seis de uso común: seno hiperbólico inverso, coseno hiperbólico inverso, tangente hiperbólica inversa, cosecante hiperbólica inversa, secante hiperbólica inversa y cotangente hiperbólica inversa. Se denotan comúnmente por los símbolos de las funciones hiperbólicas, prefijados con arc- o ar- .

Para un valor dado de una función hiperbólica, la función hiperbólica inversa proporciona la medida del ángulo hiperbólico correspondiente , por ejemplo , y La medida del ángulo hiperbólico es la longitud de un arco de una hipérbola unitaria medida en el plano de Lorentz ( no la longitud de un arco hiperbólico en el plano euclidiano ), y el doble del área del sector hiperbólico correspondiente . Esto es análogo a la forma en que la medida del ángulo circular es la longitud de arco de un arco del círculo unitario en el plano euclidiano o el doble del área del sector circular correspondiente . Alternativamente, el ángulo hiperbólico es el área de un sector de la hipérbola. Algunos autores llaman a las funciones hiperbólicas inversas funciones de área hiperbólica . ^[1]${\displaystyle \operatorname {arsinh} (\sinh a)=a}$${\displaystyle \sinh(\operatorname {arsinh} x)=x.}$ ${\displaystyle x^{2}-y^{2}=1}$${\displaystyle xy=1.}$

Las funciones hiperbólicas se utilizan en el cálculo de ángulos y distancias en la geometría hiperbólica . También se utilizan en las soluciones de muchas ecuaciones diferenciales lineales (como la ecuación que define una catenaria ), ecuaciones cúbicas y la ecuación de Laplace en coordenadas cartesianas . Las ecuaciones de Laplace son importantes en muchas áreas de la física , incluidas la teoría electromagnética , la transferencia de calor , la dinámica de fluidos y la relatividad especial .

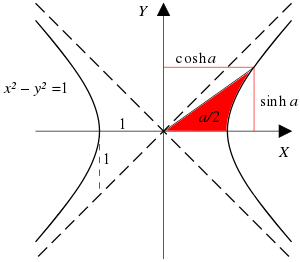
Los símbolos más antiguos y más ampliamente adoptados utilizan el prefijo arc- (es decir: arcsinh , arccosh , arctanh , arcsech , arccsch , arccoth ), por analogía con las funciones circulares inversas ( arcsin , etc.). Para una hipérbola unitaria ("círculo lorentziano") en el plano lorentziano ( plano pseudoeuclidiano de signatura (1, 1) ) ^[2] o en el plano numérico hiperbólico , ^[3] la medida del ángulo hiperbólico (argumento de las funciones hiperbólicas) es de hecho la longitud de arco de un arco hiperbólico.

También es común la notación etc., ^{[4] [5]} aunque se debe tener cuidado para evitar malas interpretaciones del superíndice −1 como exponente. La convención estándar es que o significa la función inversa mientras que o significa el recíproco Especialmente inconsistente es el uso convencional de superíndices enteros positivos para indicar un exponente en lugar de la composición de funciones, por ejemplo, convencionalmente significa y no${\displaystyle \sinh ^{-1},}$ ${\displaystyle \cosh ^{-1},}$$estilo de visualización {\sinh ^{-1}x}$${\displaystyle \sinh ^{-1}(x)}$${\displaystyle (\sinh x)^{-1}}$${\displaystyle \sinh(x)^{-1}}$ ${\displaystyle 1/\sinh x.}$$Estilo de visualización: sinh ^{2}x$${\displaystyle (\sinh x)^{2}}$ ${\displaystyle \sinh(\sinh x).}$

Debido a que el argumento de las funciones hiperbólicas no es la longitud de arco de un arco hiperbólico en el plano euclidiano , algunos autores han condenado el prefijo arc- , argumentando que debería preferirse el prefijo ar- (para área ) o arg- (para argumento ). ^[6] Siguiendo esta recomendación, las abreviaturas del estándar ISO 80000-2 utilizan el prefijo ar- (es decir: arsinh , arcosh , artanh , arsech , arcsch , arcoth ).

En los lenguajes de programación informática, las funciones circulares inversas e hiperbólicas a menudo se nombran con el prefijo más corto a- ( asinh , etc.).

En este artículo se adoptará sistemáticamente el prefijo ar- para mayor comodidad.

Dado que las funciones hiperbólicas son funciones racionales cuadráticas de la función exponencial, pueden resolverse utilizando la fórmula cuadrática y luego escribirse en términos del logaritmo natural .${\estilo de visualización \exp x,}$

${\displaystyle {\begin{aligned}\operatorname {arsinh} x&=\ln \left(x+{\sqrt {x^{2}+1}}\right)&-\infty &<x<\infty ,\\[10mu]\operatorname {arcosh} x&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&1&\leq x<\infty ,\\[10mu]\operatorname {artanh} x&={\frac {1}{2}}\ln {\frac {1+x}{1-x}}&-1&<x<1,\\[10mu]\operatorname {arcsch} x&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)&-\infty &<x<\infty ,\ x\neq 0,\\[10mu]\operatorname {arsech} x&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)&0&<x\leq 1,\\[10mu]\operatorname {arcoth} x&={\frac {1}{2}}\ln {\frac {x+1}{x-1}}&-\infty &<x<-1\ \ {\text{or}}\ \ 1<x<\infty .\end{aligned}}}$

Para argumentos complejos , las funciones circulares e hiperbólicas inversas, la raíz cuadrada y el logaritmo natural son todas funciones multivaluadas .

${\displaystyle \operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)}$

${\displaystyle \operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)}$

${\displaystyle \operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)}$

${\displaystyle \operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)}$

${\displaystyle {\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}}$

${\displaystyle {\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\pm \operatorname {arcosh} (2x^{2}+1)\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{aligned}}}$

${\displaystyle \ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)}$

${\displaystyle {\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{for}}\quad |x|>1\end{aligned}}}$

${\displaystyle \operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)}$

${\displaystyle \ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)}$^[7]

${\displaystyle \ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)}$

${\displaystyle \operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)}$

${\displaystyle \operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)}$

${\displaystyle \operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|}$

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ for all real }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ for all real }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ for all real }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ for all real }}x{\text{, except }}0\\\end{aligned}}}$

Estas fórmulas se pueden derivar en términos de las derivadas de funciones hiperbólicas. Por ejemplo, si , entonces${\displaystyle x=\sinh \theta }$${\textstyle dx/d\theta =\cosh \theta ={\sqrt {1+x^{2}}},}$

${\displaystyle {\frac {d}{dx}}\operatorname {arsinh} (x)={\frac {d\theta }{dx}}={\frac {1}{dx/d\theta }}={\frac {1}{\sqrt {1+x^{2}}}}.}$

Se pueden obtener series de expansión para las funciones anteriores:

${\displaystyle {\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}$

Una expansión asintótica para arsinh está dada por

${\displaystyle \operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}}$

Como funciones de una variable compleja , las funciones hiperbólicas inversas son funciones multivaluadas que son analíticas excepto en un número finito de puntos. Para una función de este tipo, es común definir un valor principal , que es una función analítica de un solo valor que coincide con una rama específica de la función multivaluada, sobre un dominio que consiste en el plano complejo en el que se han eliminado un número finito de arcos (generalmente semirrectas o segmentos de recta ). Estos arcos se denominan cortes de rama . El valor principal de la multifunción se elige en un punto particular y los valores en otras partes del dominio de definición se definen para que coincidan con los encontrados por continuación analítica .

Por ejemplo, para la raíz cuadrada, el valor principal se define como la raíz cuadrada que tiene una parte real positiva . Esto define una función analítica de valor único, que se define en todas partes, excepto para valores reales no positivos de las variables (donde las dos raíces cuadradas tienen una parte real cero). Este valor principal de la función raíz cuadrada se denota en lo que sigue. De manera similar, el valor principal del logaritmo, denotado en lo que sigue, se define como el valor para el cual la parte imaginaria tiene el valor absoluto más pequeño. Se define en todas partes excepto para valores reales no positivos de la variable, para los cuales dos valores diferentes del logaritmo alcanzan el mínimo.${\displaystyle {\sqrt {x}}}$${\displaystyle \operatorname {Log} }$

Para todas las funciones hiperbólicas inversas, el valor principal puede definirse en términos de los valores principales de la raíz cuadrada y de la función logaritmo. Sin embargo, en algunos casos, las fórmulas de § Definiciones en términos de logaritmos no dan un valor principal correcto, ya que dan un dominio de definición demasiado pequeño y, en un caso, no conexo .

El valor principal del seno hiperbólico inverso está dado por

${\displaystyle \operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.}$

El argumento de la raíz cuadrada es un número real no positivo, si y solo si z pertenece a uno de los intervalos [ i , + i ∞) y (− i ∞, − i ] del eje imaginario. Si el argumento del logaritmo es real, entonces es positivo. Por lo tanto, esta fórmula define un valor principal para arsinh, con cortes de rama [ i , + i ∞) y (− i ∞, − i ] . Esto es óptimo, ya que los cortes de rama deben conectar los puntos singulares i y − i hasta el infinito.

La fórmula para el coseno hiperbólico inverso dada en § Coseno hiperbólico inverso no es conveniente, ya que, de manera similar a los valores principales del logaritmo y la raíz cuadrada, el valor principal de arcosh no estaría definido para z imaginario . Por lo tanto, la raíz cuadrada debe factorizarse, lo que conduce a

${\displaystyle \operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.}$

Los valores principales de las raíces cuadradas están ambos definidos, excepto si z pertenece al intervalo real (−∞, 1] . Si el argumento del logaritmo es real, entonces z es real y tiene el mismo signo. Por lo tanto, la fórmula anterior define un valor principal de arcosh fuera del intervalo real (−∞, 1] , que es, por tanto, el único corte de rama.

Las fórmulas dadas en § Definiciones en términos de logaritmos sugieren

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right)\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned}}}$

para la definición de los valores principales de la tangente y cotangente hiperbólicas inversas. En estas fórmulas, el argumento del logaritmo es real si y solo si z es real. Para artanh, este argumento está en el intervalo real (−∞, 0] , si z pertenece a (−∞, −1] o a [1, ∞) . Para arcoth, el argumento del logaritmo está en (−∞, 0] , si y solo si z pertenece al intervalo real [−1, 1] .

Por lo tanto, estas fórmulas definen valores principales convenientes, para los cuales los cortes de rama son (−∞, −1] y [1, ∞) para la tangente hiperbólica inversa, y [−1, 1] para la cotangente hiperbólica inversa.

En vista de una mejor evaluación numérica cerca de los cortes de las ramas, algunos autores ^{[ cita requerida ]} utilizan las siguientes definiciones de los valores principales, aunque la segunda introduce una singularidad removible en z = 0 . Las dos definiciones de difieren para valores reales de con . Las de difieren para valores reales de con .${\displaystyle \operatorname {artanh} }$${\displaystyle z}$${\displaystyle z>1}$${\displaystyle \operatorname {arcoth} }$${\displaystyle z}$${\displaystyle z\in [0,1)}$

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+z}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-z}\right)\\\operatorname {arcoth} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+{\frac {1}{z}}}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-{\frac {1}{z}}}\right)\end{aligned}}}$

Para la cosecante hiperbólica inversa, el valor principal se define como

${\displaystyle \operatorname {arcsch} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1}}\,\right)}$.

Se define excepto cuando los argumentos del logaritmo y la raíz cuadrada son números reales no positivos. El valor principal de la raíz cuadrada se define entonces fuera del intervalo [− i , i ] de la recta imaginaria. Si el argumento del logaritmo es real, entonces z es un número real distinto de cero, y esto implica que el argumento del logaritmo es positivo.

Por tanto, el valor principal se define mediante la fórmula anterior fuera del corte de la rama , que consiste en el intervalo [− i , i ] de la línea imaginaria.

(En z = 0 , hay un punto singular que está incluido en el corte de la rama).

Aquí, como en el caso del coseno hiperbólico inverso, tenemos que factorizar la raíz cuadrada. Esto nos da el valor principal

${\displaystyle \operatorname {arsech} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{\sqrt {{\frac {1}{z}}-1}}\right).}$

Si el argumento de una raíz cuadrada es real, entonces z es real, y se deduce que ambos valores principales de raíces cuadradas están definidos, excepto si z es real y pertenece a uno de los intervalos (−∞, 0] y [1, +∞) . Si el argumento del logaritmo es real y negativo, entonces z también es real y negativo. Se deduce que el valor principal de arsech está bien definido, por la fórmula anterior fuera de dos cortes de rama , los intervalos reales (−∞, 0] y [1, +∞) .

Para z = 0 , hay un punto singular que está incluido en uno de los cortes de rama.

En la siguiente representación gráfica de los valores principales de las funciones hiperbólicas inversas, los cortes de las ramas aparecen como discontinuidades del color. El hecho de que todos los cortes de las ramas aparezcan como discontinuidades muestra que estos valores principales no pueden extenderse a funciones analíticas definidas en dominios más amplios. En otras palabras, los cortes de las ramas definidos anteriormente son mínimos.

• Logaritmo complejo
• Distribución secante hiperbólica
• ISO 80000-2
• Lista de integrales de funciones hiperbólicas inversas

• Herbert Busemann y Paul J. Kelly (1953) Geometría proyectiva y métrica proyectiva , página 207, Academic Press .

• "Funciones hiperbólicas inversas", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]