Grado de Turing

En informática y lógica matemática, el grado de Turing (llamado así por Alan Turing ) o grado de irresolubilidad de un conjunto de números naturales mide el nivel de irresolubilidad algorítmica del conjunto.

El concepto de grado de Turing es fundamental en la teoría de la computabilidad , donde los conjuntos de números naturales suelen considerarse problemas de decisión . El grado de Turing de un conjunto es una medida de lo difícil que es resolver el problema de decisión asociado con el conjunto, es decir, determinar si un número arbitrario está en el conjunto dado.

Dos conjuntos son equivalentes de Turing si tienen el mismo nivel de insolubilidad; cada grado de Turing es una colección de conjuntos equivalentes de Turing, de modo que dos conjuntos están en diferentes grados de Turing exactamente cuando no son equivalentes de Turing. Además, los grados de Turing están parcialmente ordenados , de modo que si el grado de Turing de un conjunto X es menor que el grado de Turing de un conjunto Y , entonces cualquier procedimiento (posiblemente no computable) que decida correctamente si los números están en Y puede convertirse efectivamente en un procedimiento que decida correctamente si los números están en X. Es en este sentido que el grado de Turing de un conjunto corresponde a su nivel de insolubilidad algorítmica.

Los grados de Turing fueron introducidos por Post (1944) y muchos resultados fundamentales fueron establecidos por Kleene y Post (1954). Los grados de Turing han sido un área de intensa investigación desde entonces. Muchas demostraciones en el área hacen uso de una técnica de demostración conocida como el método de prioridad .

En el resto de este artículo, la palabra conjunto se referirá a un conjunto de números naturales. Se dice que un conjunto X es reducible mediante el método de Turing a un conjunto Y si existe una máquina de Turing oráculo que decide la pertenencia a X cuando se le da un oráculo para la pertenencia a Y. La notación X ≤ _T Y indica que X es reducible mediante el método de Turing a Y.

Dos conjuntos X e Y se definen como equivalentes de Turing si X es reducible a Y mediante el método de Turing e Y es reducible a X mediante el método de Turing . La notación X ≡ _T Y indica que X e Y son equivalentes de Turing. La relación ≡ _T puede considerarse una relación de equivalencia , lo que significa que para todos los conjuntos X , Y y Z :

• X ≡ _TX ​
• X ≡ _T Y implica Y ≡ _T X
• Si X ≡ _T Y e Y ≡ _T Z entonces X ≡ _T Z .

Un grado de Turing es una clase de equivalencia de la relación ≡ _T . La notación [ X ] denota la clase de equivalencia que contiene un conjunto X . La colección completa de grados de Turing se denota .${\displaystyle {\mathcal {D}}}$

Los grados de Turing tienen un orden parcial ≤ definido de modo que [ X ] ≤ [ Y ] si y solo si X ≤ _T Y . Existe un único grado de Turing que contiene todos los conjuntos computables, y este grado es menor que cualquier otro grado. Se denota 0 (cero) porque es el elemento menor del conjunto parcial . (Es común usar la notación en negrita para los grados de Turing, con el fin de distinguirlos de los conjuntos. Cuando no puede producirse ninguna confusión, como con [ X ], la negrita no es necesaria).${\displaystyle {\mathcal {D}}}$

Para cualesquiera conjuntos X e Y , X join Y , escrito X ⊕ Y , se define como la unión de los conjuntos {2 n  : n ∈ X } y {2 m +1 : m ∈ Y }. El grado de Turing de X ⊕ Y es el límite superior mínimo de los grados de X e Y . Por lo tanto, es un semirretículo de unión . El límite superior mínimo de los grados a y b se denota a ∪ b . Se sabe que no es un retículo , ya que hay pares de grados sin límite inferior máximo.${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$

Para cualquier conjunto X, la notación X ′ denota el conjunto de índices de máquinas oráculo que se detienen (cuando se les da su índice como entrada) al usar X como oráculo. El conjunto X ′ se llama salto de Turing de X . El salto de Turing de un grado [ X ] se define como el grado [ X ′]; esta es una definición válida porque X ′ ≡ _T Y ′ siempre que X ≡ _T Y . Un ejemplo clave es 0 ′, el grado del problema de detención .

• Cada grado de Turing es infinito contable , es decir, contiene exactamente conjuntos.$estilo de visualización {\aleph _{0}}$
• Existen distintos grados de Turing.${\displaystyle 2^{\aleph _ {0}}}$
• Para cada grado a se cumple la desigualdad estricta a < a ′.
• Para cada grado a , el conjunto de grados inferiores a a es contable . El conjunto de grados superiores a a tiene tamaño .${\displaystyle 2^{\aleph _ {0}}}$

Se han realizado muchas investigaciones sobre la estructura de los grados de Turing. El siguiente estudio enumera solo algunos de los numerosos resultados conocidos. Una conclusión general que se puede extraer de la investigación es que la estructura de los grados de Turing es extremadamente complicada.

• Existen grados mínimos . Un grado a es mínimo si a es distinto de cero y no existe ningún grado entre 0 y a . Por lo tanto, la relación de orden en los grados no es un orden denso .
• Los grados de Turing no están ordenados linealmente por ≤ _T . ^[1]
• De hecho, por cada grado a distinto de cero hay un grado b incomparable con a .
• Hay un conjunto de grados de Turing incomparables entre pares.${\displaystyle 2^{\aleph _ {0}}}$
• Hay pares de grados sin límite inferior máximo. Por lo tanto, no es una red .${\displaystyle {\mathcal {D}}}$
• Todo conjunto parcialmente ordenado contable puede ser incluido en los grados de Turing.
• Una secuencia infinita estrictamente creciente a ₁ , a ₂ , ... de grados de Turing no puede tener un límite superior mínimo, pero siempre tiene un par exacto c , d tal que ∀ e ( e < c ∧ e < d ⇔ ∃ i e ≤ a _i ), y por lo tanto tiene límites superiores mínimos (no únicos).
• Suponiendo el axioma de constructibilidad , se puede demostrar que existe una cadena máxima de grados de tipo de orden . ^[2]${\displaystyle \omega _{1}}$

• Para cada grado a existe un grado estrictamente entre a y a′ . De hecho, existe una familia numerable de grados incomparables entre a y a′ .
• Inversión de salto: un grado a es de la forma b′ si y sólo si 0′ ≤ a .
• Para cualquier grado a existe un grado b tal que a < b y b′ = a′ ; un grado b de este tipo se llama bajo en relación a .
• Existe una secuencia infinita a _i de grados tal que a ′ _{i +1} ≤ a _i para cada i .
• El teorema de Post establece una correspondencia estrecha entre la jerarquía aritmética y los saltos de Turing finitamente iterados del conjunto vacío.

• Simpson (1977b) demostró que la teoría de primer orden de en el lenguaje ⟨ ≤, = ⟩ o ⟨ ≤, ′, = ⟩ es equivalente en muchos-uno a la teoría de la verdadera aritmética de segundo orden . Esto indica que la estructura de es extremadamente complicada.${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$
• Shore y Slaman (1999) demostraron que el operador de salto es definible en la estructura de primer orden con el lenguaje ⟨ ≤, = ⟩ .${\displaystyle {\mathcal {D}}}$

Un grado se denomina recursivamente enumerable (re) o computablemente enumerable (ce) si contiene un conjunto recursivamente enumerable . Todo grado re está por debajo de 0′ , pero no todo grado por debajo de 0′ es re. Sin embargo, un conjunto es reducible a 0′ mediante muchos-uno si y solo si es re. ^[3]${\estilo de visualización A}$${\estilo de visualización A}$

• Sacks (1964): Los grados re son densos; entre dos grados re hay un tercer grado re.
• Lachlan (1966a) y Yates (1966): Hay dos grados re sin límite inferior máximo en los grados re.
• Lachlan (1966a) y Yates (1966): Hay un par de grados re distintos de cero cuyo límite inferior máximo es 0 .
• Lachlan (1966b): No existe ningún par de grados re cuyo límite inferior máximo sea 0 y cuyo límite superior mínimo sea 0′ . Este resultado se denomina informalmente teorema del no diamante .
• Thomason (1971): Toda red distributiva finita puede ser incorporada en los grados re. De hecho, el álgebra booleana numerable y sin átomos puede ser incorporada de una manera que preserve suprema e ínfima .
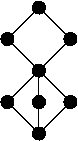
• Lachlan y Soare (1980): No todas las redes finitas pueden ser incrustadas en los grados re (a través de una incrustación que preserva suprema e ínfima). Un ejemplo particular se muestra a la derecha. LA Harrington y TA Slaman (ver Nies, Shore y Slaman (1998)): La teoría de primer orden de los grados re en el lenguaje ⟨ 0 , ≤, = ⟩ es equivalente en muchos-uno a la teoría de la verdadera aritmética de primer orden .

Además, existe el lema del límite de Shoenfield, que establece que un conjunto A satisface si y solo si existe una "aproximación recursiva" a su función característica: una función g tal que para s suficientemente grande , . ^[4]${\displaystyle [A]\leq _{T}\conjunto vacío '}$${\displaystyle g(s)=\chi_{A}(s)}$

Un conjunto A se llama n -r e. si existe una familia de funciones tales que: ^[4]${\displaystyle (A_{s})_{s\in \mathbb {N} }}$

• A _s es una aproximación recursiva de A : para algún t , para cualquier s ≥ t tenemos A _s ( x ) = A ( x ), en particular confundiendo A con su función característica. (Si eliminamos esta condición obtenemos una definición de A como "débilmente n -re" )
• A _s es un " predicado de n -ensayos": para todo x , A ₀ ( x )=0 y la cardinalidad de es ≤n.${\displaystyle \{s\mid A_{s}(x)\neq A_{s+1}(x)\}}$

Propiedades de los grados n -re: ^[4]

• La clase de conjuntos de grado n -re es una subclase estricta de la clase de conjuntos de grado ( n + 1)-re.
• Para todo n > 1 hay dos ( n +1)-re grados a , b con , tales que el segmento no contiene ningún n -re grados.${\displaystyle \mathbf {a} \leq _{T}\mathbf {b} }$${\displaystyle \{\mathbf {c} \mid \mathbf {a} \leq _{T}\mathbf {c} \leq _{T}\mathbf {b} \}}$
• ${\estilo de visualización A}$y son ( n + 1)-re si y solo si ambos conjuntos son débilmente- n -re${\displaystyle {\overline {A}}}$

Emil Post estudió los grados de Turing de re y se preguntó si existe algún grado de re estrictamente entre 0 y 0′ . El problema de construir dicho grado (o demostrar que no existe) se conoció como el problema de Post . Este problema fue resuelto independientemente por Friedberg y Muchnik en la década de 1950, quienes demostraron que estos grados intermedios de re existen ( teorema de Friedberg-Muchnik ). Sus demostraciones desarrollaron el mismo nuevo método para construir grados de re, que llegó a conocerse como el método de prioridad . El método de prioridad es ahora la técnica principal para establecer resultados sobre conjuntos de re.

La idea del método de prioridad para construir un re-set X es listar una secuencia contable de requisitos que X debe satisfacer. Por ejemplo, para construir un re-set X entre 0 y 0′ es suficiente satisfacer los requisitos A _e y B _e para cada número natural e , donde A _e requiere que la máquina oráculo con índice e no calcule 0′ a partir de X y B _e requiere que la máquina de Turing con índice e (y sin oráculo) no calcule X . Estos requisitos se colocan en un orden de prioridad , que es una biyección explícita de los requisitos y los números naturales. La prueba procede inductivamente con una etapa para cada número natural; estas etapas pueden considerarse como pasos de tiempo durante los cuales se enumera el conjunto X. En cada etapa, se pueden colocar números en X o se puede evitar para siempre (si no se daña) que entren en X en un intento de satisfacer los requisitos (es decir, forzarlos a que se mantengan una vez que se haya enumerado todo X ). A veces, se puede enumerar un número en X para satisfacer un requisito, pero al hacerlo se provocaría que un requisito previamente satisfecho se volviera insatisfecho (es decir, se lesionara ). El orden de prioridad de los requisitos se utiliza para determinar qué requisito satisfacer en este caso. La idea informal es que si un requisito se lesiona, eventualmente dejará de lesionarse después de que todos los requisitos de mayor prioridad hayan dejado de lesionarse, aunque no todos los argumentos de prioridad tienen esta propiedad. Se debe argumentar que el conjunto general X es re y satisface todos los requisitos. Los argumentos de prioridad se pueden utilizar para probar muchos hechos sobre los conjuntos re; los requisitos utilizados y la manera en que se satisfacen deben elegirse cuidadosamente para producir el resultado requerido.

Por ejemplo, una simple (y por lo tanto no computable re) baja X (baja significa X ′=0′) se puede construir en infinitas etapas de la siguiente manera. Al comienzo de la etapa n , sea T _n la cinta de salida (binaria), identificada con el conjunto de índices de celda donde colocamos 1 hasta ahora (por lo que X =∪ _n T _n ; T ₀ =∅); y sea P _n ( m ) la prioridad para no emitir 1 en la ubicación m ; P ₀ ( m )=∞. En la etapa n , si es posible (de lo contrario, no haga nada en la etapa), elija el menor i < n tal que ∀ m P _n ( m )≠ i y la máquina de Turing i se detenga en < n pasos en alguna entrada S ⊇ T _n con ∀ m ∈ S \ T _n P _n ( m )≥ i . Elija cualquiera de estos (finitos) S , establezca T _{n +1} = S , y para cada celda m visitada por la máquina i en S , establezca P _{n +1} ( m ) = min( i , P _n ( m )), y establezca todas las prioridades > i a ∞, y luego establezca una celda de prioridad ∞ (cualquiera servirá) que no esté en S a la prioridad i . Esencialmente, hacemos que la máquina i se detenga si podemos hacerlo sin alterar las prioridades < i , y luego establecemos prioridades para evitar que las máquinas > i interrumpan la detención; todas las prioridades son eventualmente constantes.

Para ver que X es bajo, la máquina i se detiene en X si y solo si se detiene en < n pasos en algún T _n tal que las máquinas < i que se detienen en X lo hacen en < n - i pasos (por recursión, esto es uniformemente computable desde 0′). X no es computable ya que de lo contrario una máquina de Turing podría detenerse en Y si y solo si Y \ X no está vacío, lo que contradice la construcción ya que X excluye algunas celdas de prioridad i para i arbitrariamente grande ; y X es simple porque para cada i el número de celdas de prioridad i es finito.

• Medida de Martín

• Cooper, SB (2004). Teoría de la computabilidad . Boca Raton, FL: Chapman & Hall/CRC. pág. 424. ISBN 1-58488-237-9.
• Cutland, Nigel J. (1980). Computabilidad, una introducción a la teoría de funciones recursivas . Cambridge-Nueva York: Cambridge University Press. pág. 251. ISBN 0-521-22384-9.; ISBN 0-521-29465-7 

• Ambos-Spies, Klaus; Fejer, Peter (20 de marzo de 2006). "Grados de insolubilidad" (PDF) . Consultado el 20 de agosto de 2023. Inédito .
• Epstein, RL; Haas, R; Kramer, LR (1981). Leman, M; Schmerl, J.; Soare, R. (eds.). Jerarquías de conjuntos y grados por debajo de 0. Apuntes de clase en matemáticas. Vol. 859. Springer-Verlag.
• Lerman, M. (1983). Grados de insolubilidad. Perspectivas en lógica matemática . Berlín: Springer-Verlag. ISBN 3-540-12155-2.
• Odifreddi, Piergiorgio (1989). Teoría de la recursión clásica . Estudios de lógica y fundamentos de las matemáticas. Vol. 125. Ámsterdam: Holanda Septentrional. ISBN 978-0-444-87295-1.Sr .  0982269.
• Odifreddi, Piergiorgio (1999). Teoría clásica de la recursión. Vol. II . Estudios de lógica y fundamentos de las matemáticas. Vol. 143. Ámsterdam: Holanda Septentrional. ISBN 978-0-444-50205-6.Señor 1718169  .
• Rogers, Hartley (1967). Teoría de funciones recursivas y computabilidad efectiva . Cambridge, Massachusetts : MIT Press . ISBN. 9780262680523. OCLC  933975989 . Consultado el 6 de mayo de 2020 .
• Sacks, GE (1966). Grados de insolubilidad . Anales de estudios matemáticos. Princeton University Press. ISBN 978-0-6910-7941-7.JSTOR j.ctt1b9x0r8  .
• Simpson, Steven G. (1977a). "Grados de insolubilidad : un estudio de los resultados". Anales de estudios matemáticos . Estudios de lógica y fundamentos de las matemáticas. 90. Elsevier : 631–652. doi :10.1016/S0049-237X(08)71117-0. ISBN 9780444863881.
• Shoenfield, Joseph R. (1971). Grados de insolubilidad . North-Holland/Elsevier. ISBN 978-0-7204-2061-6.
• Shore, R. (1993). "Las teorías de los grados T, tt y wtt: indecidibilidad y más allá". En Univ. Nac. del Sur, Bahía Blanca (ed.). Actas del IX Simposio Latinoamericano de Lógica Matemática, Parte 1 (Bahía Blanca, 1992) . Notas Lógica Mat. Vol. 38. pp. 61–70.
• Soare, Robert Irving (1987). Conjuntos y grados recursivamente enumerables: un estudio de funciones computables y conjuntos generados computacionalmente . Perspectivas en lógica matemática. Berlín: Springer-Verlag. ISBN 3-540-15299-7.
• Soare, Robert Irving (1978). "Conjuntos y grados enumerables recursivamente". Bull. Amer. Math. Soc . 84 (6): 1149–1181. doi : 10.1090/S0002-9904-1978-14552-2 . MR  0508451. S2CID  29549997.

• Chong, CT; Yu, Liang (diciembre de 2007). "Cadenas máximas en los grados de Turing". Journal of Symbolic Logic . 72 (4): 1219–1227. doi :10.2178/jsl/1203350783. JSTOR  27588601. S2CID  38576214.
• DeAntonio, Jasper (24 de septiembre de 2010). "Los grados de Turing y su falta de orden lineal" (PDF) . Consultado el 20 de agosto de 2023 .
• Kleene, Stephen Cole ; Post, Emil L. (1954), "La semired superior de grados de irresolubilidad recursiva", Anales de Matemáticas , Segunda serie, 59 (3): 379–407, doi :10.2307/1969708, ISSN  0003-486X, JSTOR  1969708, MR  0061078
• Lachlan, Alistair H. (1966a), "Límites inferiores para pares de grados recursivamente enumerables", Actas de la London Mathematical Society , 3 (1): 537–569, CiteSeerX  10.1.1.106.7893 , doi :10.1112/plms/s3-16.1.537.
• Lachlan, Alistair H. (1966b), "La imposibilidad de encontrar complementos relativos para grados recursivamente enumerables", J. Symb. Log. , 31 (3): 434–454, doi :10.2307/2270459, JSTOR  2270459, S2CID  30992462.
• Lachlan, Alistair H.; Soare, Robert Irving (1980), "No todas las redes finitas son integrables en los grados recursivamente enumerables", Advances in Mathematics , 37 : 78–82, doi : 10.1016/0001-8708(80)90027-4
• Nies, André; Shore, Richard A.; Slaman, Theodore A. (1998), "Interpretabilidad y definibilidad en los grados recursivamente enumerables", Actas de la London Mathematical Society , 77 (2): 241–291, CiteSeerX  10.1.1.29.9588 , doi :10.1112/S002461159800046X, ISSN  0024-6115, MR  1635141, S2CID  16488410
• Post, Emil L. (1944), "Conjuntos enumerables recursivamente de números enteros positivos y sus problemas de decisión", Boletín de la American Mathematical Society , 50 (5): 284–316, doi : 10.1090/S0002-9904-1944-08111-1 , ISSN  0002-9904, MR  0010514
• Sacks, GE (1964), "Los grados recursivamente enumerables son densos", Anales de Matemáticas , Segunda Serie, 80 (2): 300–312, doi :10.2307/1970393, JSTOR  1970393
• Shore, Richard A. ; Slaman, Theodore A. (1999), "Definición del salto de Turing", Mathematical Research Letters , 6 (6): 711–722, doi : 10.4310/mrl.1999.v6.n6.a10 , ISSN  1073-2780, MR  1739227
• Simpson, Stephen G. (1977b). "Teoría de primer orden de los grados de irresolubilidad recursiva". Anales de Matemáticas . Segunda serie. 105 (1): 121–139. doi :10.2307/1971028. ISSN  0003-486X. JSTOR  1971028. MR  0432435.
• Thomason, SK (1971), "Subredes de los grados recursivamente enumerables", Z. Math. Logik Grundlag. Math. , 17 : 273–280, doi :10.1002/malq.19710170131
• Yates, CEM (1966), "Un par mínimo de grados enumerables recursivamente", Journal of Symbolic Logic , 31 (2): 159–168, doi :10.2307/2269807, JSTOR  2269807, S2CID  38778059