Enrejado (orden)

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Por favor, ayude a mejorar este artículo introduciendo citas más precisas. ( Mayo de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Relaciones binarias transitivas en a mi
Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Total, Semiconnex Anti- reflexivo Relación de equivalencia Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado (cuasi pedido) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Orden parcial ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado total ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Pedido total ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Preordenamiento de pozos ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Bien-cuasi-ordenamiento ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Buen orden ✗ Y Y Y ✗ ✗ Y ✗ ✗ Enrejado ✗ Y ✗ ✗ Y Y Y ✗ ✗ Unión de semirrejilla ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Conocer-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Orden parcial estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden débil estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden total estricta ✗ Y Y ✗ ✗ ✗ ✗ Y Y Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Definiciones, para todos y${\estilo de visualización a,b}$${\displaystyle S\neq \varnothing :}$ ${\displaystyle {\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}aRb{\text{ y }}&bRa\\\Rightarrow a={}&b\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ o }}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}\min S\\{\text{existe}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\vee b\\{\text{existe}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\wedge b\\{\text{existe}}\end{aligned}}}$ ${\estilo de visualización aRa}$ ${\displaystyle {\text{no }}aRa}$ ${\displaystyle {\begin{aligned}aRb\Rightarrow \\{\text{no }}bRa\end{aligned}}}$
Yindica que la propiedad de la columna siempre es verdadera para el término de la fila (a la izquierda), mientras que ✗ indica que la propiedad no está garantizada en general (puede cumplirse o no). Por ejemplo, que toda relación de equivalencia es simétrica, pero no necesariamente antisimétrica, se indica con en la columna "Simétrica" ​​y ✗ en la columna "Antisimétrica", respectivamente.Y Todas las definiciones requieren tácitamente que la relación homogénea sea transitiva : para todo si y entonces La definición de un término puede requerir propiedades adicionales que no están incluidas en esta tabla.${\estilo de visualización R}$${\estilo de visualización a,b,c,}$$Estilo de visualización aRb$${\estilo de visualización bRc}$${\estilo de visualización aRc.}$

Estructuras algebraicas
Como un grupo Grupo Semigrupo  / Monoide Bastidor y rueda Cuasigrupo y bucle Grupo abeliano Magma Grupo de mentiras Teoría de grupos
En forma de anillo Anillo Rango de frecuencia Semianillo Cerca del anillo Anillo conmutativo Dominio Dominio integral Campo Anillo de división Anillo de mentira Teoría de anillos
En forma de celosía Enrejado Semirretículo Celosía complementada Pedido total Álgebra de Heyting Álgebra de Boole Mapa de celosías Teoría de celosía
Similar a un módulo Módulo Grupo con operadores Espacio vectorial Álgebra lineal
Similar al álgebra Álgebra De asociación No asociativo Álgebra de composición Álgebra de Lie Calificado Biálgebra Álgebra de Hopf
en a mi

Un retículo es una estructura abstracta estudiada en las subdisciplinas matemáticas de la teoría del orden y el álgebra abstracta . Consiste en un conjunto parcialmente ordenado en el que cada par de elementos tiene un supremo único (también llamado límite inferior mínimo o unión ) y un ínfimo único (también llamado límite inferior máximo o encuentro ). Un ejemplo lo da el conjunto potencia de un conjunto, parcialmente ordenado por inclusión , para el que el supremo es la unión y el ínfimo es la intersección . Otro ejemplo lo dan los números naturales , parcialmente ordenados por divisibilidad , para los que el supremo es el mínimo común múltiplo y el ínfimo es el máximo común divisor .

Las retículas también pueden caracterizarse como estructuras algebraicas que satisfacen ciertas identidades axiomáticas . Dado que las dos definiciones son equivalentes, la teoría de retículas se basa tanto en la teoría del orden como en el álgebra universal . Las semirretículas incluyen retículas, que a su vez incluyen las álgebras de Heyting y de Boole . Todas estas estructuras de tipo retícula admiten descripciones tanto teóricas del orden como algebraicas.

El subcampo del álgebra abstracta que estudia los retículos se llama teoría de retículos .

Una red puede definirse desde el punto de vista teórico como un conjunto parcialmente ordenado o como una estructura algebraica.

Un conjunto parcialmente ordenado (poset) se denomina retículo si es a la vez un semirretículo de unión y de encuentro , es decir, cada subconjunto de dos elementos tiene un semirretículo de unión (es decir, el límite superior mínimo, denotado por ) y dualmente un encuentro (es decir, el límite inferior máximo, denotado por ). Esta definición hace que y operaciones binarias . Ambas operaciones son monótonas con respecto al orden dado: y implica que y${\displaystyle (L,\leq )}$${\displaystyle \{a,b\}\subseteq L}$${\displaystyle a\vee b}$${\displaystyle a\wedge b}$${\displaystyle \,\wedge \,}$${\displaystyle \,\vee \,}$ ${\displaystyle a_{1}\leq a_{2}}$${\displaystyle b_{1}\leq b_{2}}$${\displaystyle a_{1}\vee b_{1}\leq a_{2}\vee b_{2}}$${\displaystyle a_{1}\wedge b_{1}\leq a_{2}\wedge b_{2}.}$

De ello se deduce, mediante un argumento de inducción , que todo subconjunto finito no vacío de una red tiene un límite superior mínimo y un límite inferior máximo. Con suposiciones adicionales, pueden ser posibles otras conclusiones; véase Completitud (teoría del orden) para una discusión más amplia de este tema. Ese artículo también analiza cómo se puede reformular la definición anterior en términos de la existencia de conexiones de Galois adecuadas entre conjuntos parcialmente ordenados relacionados, un enfoque de especial interés para el enfoque de la teoría de categorías de las redes y para el análisis de conceptos formales .

Dado un subconjunto de una red, las funciones de encuentro y unión se restringen a funciones parciales ; no están definidas si su valor no está en el subconjunto. La estructura resultante se denomina${\displaystyle H\subseteq L,}$${\displaystyle H.}$${\displaystyle H}$red parcial . Además de esta definición extrínseca como un subconjunto de alguna otra estructura algebraica (una red), una red parcial también puede definirse intrínsecamente como un conjunto con dos operaciones binarias parciales que satisfacen ciertos axiomas.^[1]

Una red es una estructura algebraica , que consta de un conjunto y dos operaciones binarias, conmutativas y asociativas y que satisface las siguientes identidades axiomáticas para todos los elementos (a veces llamadas leyes de absorción ):${\displaystyle (L,\vee ,\wedge )}$${\displaystyle L}$ ${\displaystyle \vee }$${\displaystyle \wedge }$${\displaystyle L}$${\displaystyle a,b\in L}$$${\displaystyle a\vee (a\wedge b)=a}$$$${\displaystyle a\wedge (a\vee b)=a}$$

Las dos identidades siguientes también suelen considerarse axiomas, aunque se deduzcan de las dos leyes de absorción tomadas en conjunto. ^[2] Éstas se denominan leyes idempotentes .$${\displaystyle a\vee a=a}$$$${\displaystyle a\wedge a=a}$$

Estos axiomas afirman que tanto y son semirretículos . Las leyes de absorción, los únicos axiomas anteriores en los que aparecen tanto el encuentro como la unión, distinguen un retículo de un par arbitrario de estructuras de semirretículos y aseguran que los dos semirretículos interactúan apropiadamente. En particular, cada semirretículo es el dual del otro. Las leyes de absorción pueden verse como un requisito de que los semirretículos de encuentro y unión definan el mismo orden parcial .${\displaystyle (L,\vee )}$${\displaystyle (L,\wedge )}$

Una red de teoría de orden da lugar a las dos operaciones binarias y, dado que las leyes conmutativa, asociativa y de absorción se pueden verificar fácilmente para estas operaciones, forman una red en el sentido algebraico.${\displaystyle \vee }$${\displaystyle \wedge .}$${\displaystyle (L,\vee ,\wedge )}$

El recíproco también es cierto. Dada una red definida algebraicamente, se puede definir un orden parcial en estableciendo para todos los elementos Las leyes de absorción garantizan que ambas definiciones sean equivalentes: y dualmente para la otra dirección.${\displaystyle (L,\vee ,\wedge ),}$${\displaystyle \leq }$${\displaystyle L}$$${\displaystyle a\leq b{\text{ if }}a=a\wedge b,{\text{ or }}}$$$${\displaystyle a\leq b{\text{ if }}b=a\vee b,}$$${\displaystyle a,b\in L.}$$${\displaystyle a=a\wedge b{\text{ implies }}b=b\vee (b\wedge a)=(a\wedge b)\vee b=a\vee b}$$

Ahora se puede comprobar que la relación introducida de esta manera define un ordenamiento parcial dentro del cual se dan encuentros y uniones binarias a través de las operaciones originales y${\displaystyle \leq }$${\displaystyle \vee }$${\displaystyle \wedge .}$

Dado que las dos definiciones de red son equivalentes, uno puede invocar libremente aspectos de cualquiera de las definiciones de cualquier manera que se ajuste al propósito en cuestión.

Una red acotada es una red que además tiene un elemento mayor (también llamado máximo o elemento superior , y denotado por o por ) y un elemento menor (también llamado mínimo o inferior , denotado por o por ), que satisfacen${\displaystyle 1,}$${\displaystyle \top }$${\displaystyle 0}$${\displaystyle \bot }$$${\displaystyle 0\leq x\leq 1\;{\text{ for every }}x\in L.}$$

Una red acotada también puede definirse como una estructura algebraica de la forma tal que es una red, (la parte inferior de la red) es el elemento identidad para la operación de unión y (la parte superior de la red) es el elemento identidad para la operación de encuentro.${\displaystyle (L,\vee ,\wedge ,0,1)}$${\displaystyle (L,\vee ,\wedge )}$${\displaystyle 0}$${\displaystyle \vee ,}$${\displaystyle 1}$${\displaystyle \wedge .}$$${\displaystyle a\vee 0=a}$$$${\displaystyle a\wedge 1=a}$$

Un conjunto parcialmente ordenado es una red acotada si y solo si cada conjunto finito de elementos (incluido el conjunto vacío) tiene una unión y un encuentro. Para cada elemento de un conjunto parcial es vacuamente cierto que y y por lo tanto cada elemento de un conjunto parcial es tanto un límite superior como un límite inferior del conjunto vacío. Esto implica que la unión de un conjunto vacío es el elemento menor y el encuentro del conjunto vacío es el elemento mayor Esto es consistente con la asociatividad y conmutatividad de encuentro y unión: la unión de una unión de conjuntos finitos es igual a la unión de las uniones de los conjuntos, y dualmente, el encuentro de una unión de conjuntos finitos es igual al encuentro de los encuentros de los conjuntos, es decir, para subconjuntos finitos y de un conjunto parcial y se mantienen. Tomando como el conjunto vacío, y lo cual es consistente con el hecho de que${\displaystyle x}$${\displaystyle {\text{ for all }}a\in \varnothing ,x\leq a}$${\displaystyle {\text{ for all }}a\in \varnothing ,a\leq x,}$${\textstyle \bigvee \varnothing =0,}$${\textstyle \bigwedge \varnothing =1.}$${\displaystyle A}$${\displaystyle B}$${\displaystyle L,}$$${\displaystyle \bigvee (A\cup B)=\left(\bigvee A\right)\vee \left(\bigvee B\right)}$$$${\displaystyle \bigwedge (A\cup B)=\left(\bigwedge A\right)\wedge \left(\bigwedge B\right)}$$${\displaystyle B}$$${\displaystyle \bigvee (A\cup \varnothing )=\left(\bigvee A\right)\vee \left(\bigvee \varnothing \right)=\left(\bigvee A\right)\vee 0=\bigvee A}$$$${\displaystyle \bigwedge (A\cup \varnothing )=\left(\bigwedge A\right)\wedge \left(\bigwedge \varnothing \right)=\left(\bigwedge A\right)\wedge 1=\bigwedge A,}$$${\displaystyle A\cup \varnothing =A.}$

Cada red se puede incluir en una red acotada añadiendo un elemento mayor y un elemento menor. Además, toda red finita no vacía se acota tomando la unión (respectivamente, encuentro) de todos los elementos, denotada por (respectivamente ) donde es el conjunto de todos los elementos.${\textstyle 1=\bigvee L=a_{1}\lor \cdots \lor a_{n}}$${\textstyle 0=\bigwedge L=a_{1}\land \cdots \land a_{n}}$${\displaystyle L=\left\{a_{1},\ldots ,a_{n}\right\}}$

Las redes tienen algunas conexiones con la familia de estructuras algebraicas de tipo grupo . Debido a que la reunión y la unión conmutan y asocian, una red puede considerarse como formada por dos semigrupos conmutativos que tienen el mismo dominio. Para una red acotada, estos semigrupos son de hecho monoides conmutativos . La ley de absorción es la única identidad definitoria que es peculiar de la teoría de redes. Una red acotada también puede considerarse como una red conmutativa sin el axioma distributivo.

Por conmutatividad, asociatividad e idempotencia se puede pensar en la unión y el encuentro como operaciones sobre conjuntos finitos no vacíos, en lugar de sobre pares de elementos. En una red acotada, la unión y el encuentro del conjunto vacío también se pueden definir (como y respectivamente). Esto hace que las redes acotadas sean algo más naturales que las redes generales, y muchos autores exigen que todas las redes sean acotadas.${\displaystyle 0}$${\displaystyle 1,}$

La interpretación algebraica de los retículos desempeña un papel esencial en el álgebra universal . ^{[ cita requerida ]}

• 
  Imagen 1: Subconjuntos de la inclusión de subconjuntos . El nombre "retículo" se debe a la forma del diagrama de Hasse que lo representa.${\displaystyle \{x,y,z\},}$
• 
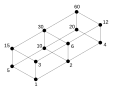
  Imagen 2: Retícula de divisores enteros de 60, ordenados por " divide ".
• 
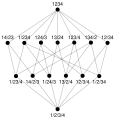
  Imagen 3: Retícula de particiones ordenadas por " refina ".${\displaystyle \{1,2,3,4\},}$
• 
  Imagen 4: Red de números enteros positivos, ordenados por${\displaystyle \,\leq ,}$
• 
  Imagen 5: Red de pares de números enteros no negativos, ordenados por componentes.

• Para cualquier conjunto , la colección de todos los subconjuntos de (denominada el conjunto potencia de ) se puede ordenar mediante la inclusión de subconjuntos para obtener una red acotada por sí misma y el conjunto vacío. En esta red, el supremo se obtiene mediante la unión de conjuntos y el ínfimo mediante la intersección de conjuntos (véase la figura 1).${\displaystyle A,}$${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$
• Para cualquier conjunto, la colección de todos los subconjuntos finitos de un conjunto ordenado por inclusión también es una red, y estará acotada si y sólo si es finito.${\displaystyle A,}$${\displaystyle A,}$${\displaystyle A}$
• Para cualquier conjunto, la colección de todas las particiones de ordenado por refinamiento , es una red (ver Figura 3).${\displaystyle A,}$${\displaystyle A,}$
• Los números enteros positivos en su orden habitual forman una red ilimitada, bajo las operaciones de "min" y "max". 1 es inferior; no hay superior (ver figura 4).
• El cuadrado cartesiano de los números naturales, ordenado de tal manera que si el par es el elemento inferior, no hay superior (ver figura 5).${\displaystyle (a,b)\leq (c,d)}$${\displaystyle a\leq c{\text{ and }}b\leq d.}$${\displaystyle (0,0)}$
• Los números naturales también forman una red bajo las operaciones de tomar el máximo común divisor y el mínimo común múltiplo , con la divisibilidad como relación de orden: si divide es inferior; es superior. La figura 2 muestra una subred finita.${\displaystyle a\leq b}$${\displaystyle a}$${\displaystyle b.}$ ${\displaystyle 1}$${\displaystyle 0}$
• Toda red completa (véase también más abajo) es una red acotada (bastante específica). Esta clase da lugar a una amplia gama de ejemplos prácticos .
• El conjunto de elementos compactos de un retículo aritmético completo es un retículo con un elemento mínimo, donde las operaciones del retículo se dan restringiendo las operaciones respectivas del retículo aritmético. Esta es la propiedad específica que distingue a los retículos aritméticos de los retículos algebraicos , para los cuales los compactos solo forman un semirretículo de unión . Ambas clases de retículos completos se estudian en la teoría de dominios .

Se dan más ejemplos de redes para cada una de las propiedades adicionales que se analizan a continuación.

La mayoría de los conjuntos parcialmente ordenados no son redes, incluidos los siguientes.

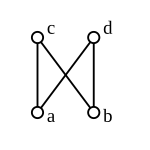
• Un conjunto de elementos discretos, es decir, un conjunto de elementos que implica que es un retículo si y solo si tiene como máximo un elemento. En particular, el conjunto de elementos discreto de dos elementos no es un retículo.${\displaystyle x\leq y}$${\displaystyle x=y,}$
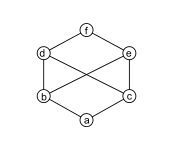
• Aunque el conjunto parcialmente ordenado por divisibilidad es un retículo, el conjunto así ordenado no es un retículo porque el par 2, 3 carece de unión; de manera similar, 2, 3 carece de una unión en${\displaystyle \{1,2,3,6\}}$${\displaystyle \{1,2,3\}}$${\displaystyle \{2,3,6\}.}$
• El conjunto parcialmente ordenado por divisibilidad no es un retículo. Todo par de elementos tiene un límite superior y un límite inferior, pero el par 2, 3 tiene tres límites superiores, a saber, 12, 18 y 36, ninguno de los cuales es el menor de esos tres bajo divisibilidad (12 y 18 no se dividen entre sí). Del mismo modo, el par 12, 18 tiene tres límites inferiores, a saber, 1, 2 y 3, ninguno de los cuales es el mayor de esos tres bajo divisibilidad (2 y 3 no se dividen entre sí).${\displaystyle \{1,2,3,12,18,36\}}$

La noción apropiada de un morfismo entre dos retículos se desprende fácilmente de la definición algebraica anterior. Dados dos retículos y un homomorfismo reticular de L a M es una función tal que para todo${\displaystyle \left(L,\vee _{L},\wedge _{L}\right)}$${\displaystyle \left(M,\vee _{M},\wedge _{M}\right),}$${\displaystyle f:L\to M}$${\displaystyle a,b\in L:}$$${\displaystyle f\left(a\vee _{L}b\right)=f(a)\vee _{M}f(b),{\text{ and }}}$$$${\displaystyle f\left(a\wedge _{L}b\right)=f(a)\wedge _{M}f(b).}$$

Por lo tanto, se trata de un homomorfismo de las dos semirredes subyacentes . Cuando se consideran retículas con más estructura, los morfismos también deberían "respetar" la estructura adicional. En particular, un homomorfismo de retícula acotada (normalmente llamado simplemente "homomorfismo de retícula") entre dos retículas acotadas también debería tener la siguiente propiedad:${\displaystyle f}$${\displaystyle f}$${\displaystyle L}$${\displaystyle M}$$${\displaystyle f\left(0_{L}\right)=0_{M},{\text{ and }}}$$$${\displaystyle f\left(1_{L}\right)=1_{M}.}$$

En la formulación de la teoría del orden, estas condiciones simplemente establecen que un homomorfismo de retículos es una función que preserva los encuentros y las uniones binarias. Para retículos acotados, la preservación de los elementos mínimo y máximo es simplemente la preservación de los encuentros y las uniones del conjunto vacío.

Cualquier homomorfismo de redes es necesariamente monótono con respecto a la relación de ordenación asociada; véase Función que preserva el límite . Lo inverso no es cierto: la monotonía de ninguna manera implica la preservación requerida de encuentros y junturas (véase Figura 9), aunque una biyección que preserva el orden es un homomorfismo si su inversa también preserva el orden.

Dada la definición estándar de isomorfismos como morfismos invertibles, un isomorfismo reticular es simplemente un homomorfismo reticular biyectivo . De manera similar, un endomorfismo reticular es un homomorfismo reticular de un retículo hacia sí mismo, y un automorfismo reticular es un endomorfismo reticular biyectivo. Los retículos y sus homomorfismos forman una categoría .

Sean y dos retículos con 0 y 1. Un homomorfismo de a se llama 0 , 1 - separando si y solo si ( separa 0 ) y ( separa 1).${\displaystyle \mathbb {L} }$${\displaystyle \mathbb {L} '}$${\displaystyle \mathbb {L} }$${\displaystyle \mathbb {L} '}$ ${\displaystyle f^{-1}\{f(0)\}=\{0\}}$${\displaystyle f}$${\displaystyle f^{-1}\{f(1)\}=\{1\}}$${\displaystyle f}$

Una subred de una red es un subconjunto de que es una red con las mismas operaciones de encuentro y unión que Es decir, si es una red y es un subconjunto de tal que para cada par de elementos tanto y están en entonces es una subred de ^[3]${\displaystyle L}$${\displaystyle L}$${\displaystyle L.}$${\displaystyle L}$${\displaystyle M}$${\displaystyle L}$${\displaystyle a,b\in M}$${\displaystyle a\wedge b}$${\displaystyle a\vee b}$${\displaystyle M,}$${\displaystyle M}$${\displaystyle L.}$

Una subred de una red es una subred convexa de si e implica que pertenece a para todos los elementos${\displaystyle M}$${\displaystyle L}$${\displaystyle L,}$${\displaystyle x\leq z\leq y}$${\displaystyle x,y\in M}$${\displaystyle z}$${\displaystyle M,}$${\displaystyle x,y,z\in L.}$

Ahora presentamos una serie de propiedades importantes que conducen a clases especiales de redes interesantes. Una de ellas, la acotación, ya se ha analizado.

Un conjunto parcial se denomina red completa si todos sus subconjuntos tienen una unión y un encuentro. En particular, cada red completa es una red acotada. Si bien los homomorfismos de red acotados en general conservan solo las uniones y los encuentros finitos, se requieren homomorfismos de red completos para conservar las uniones y los encuentros arbitrarios.

Todo conjunto parcial que sea un semirretículo completo es también un retículo completo. Relacionado con este resultado está el interesante fenómeno de que existen varias nociones en competencia de homomorfismo para esta clase de conjuntos parciales, dependiendo de si se los considera retículos completos, semirretículos de unión completos, semirretículos de encuentro completos o retículos de unión completos o de encuentro completos.

"Red parcial" no es lo opuesto a "red completa"; más bien, "red parcial", "red" y "red completa" son definiciones cada vez más restrictivas.

Una red condicionalmente completa es una red en la que cada subconjunto no vacío que tiene un límite superior tiene una unión (es decir, un límite superior mínimo). Tales redes proporcionan la generalización más directa del axioma de completitud de los números reales . Una red condicionalmente completa es una red completa, o una red completa sin su elemento máximo ni su elemento mínimo , o ambas. ^{[4] [5]}${\displaystyle 1,}$${\displaystyle 0,}$

Como las redes vienen con dos operaciones binarias, es natural preguntar si una de ellas se distribuye sobre la otra, es decir, si una u otra de las siguientes leyes duales se cumple para cada tres elementos :${\displaystyle a,b,c\in L,}$

Distributividad de sobre${\displaystyle \vee }$${\displaystyle \wedge }$

$${\displaystyle a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c).}$$

Distributividad de sobre${\displaystyle \wedge }$${\displaystyle \vee }$

$${\displaystyle a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c).}$$

Una red que satisface el primer o, equivalentemente (como se ha demostrado), el segundo axioma, se denomina red distributiva . Las únicas redes no distributivas con menos de 6 elementos se denominan M ₃ y N ₅ ; ^[6] se muestran en las figuras 10 y 11, respectivamente. Una red es distributiva si y solo si no tiene una subred isomorfa a M ₃ o N ₅ . ^[7] Cada red distributiva es isomorfa a una red de conjuntos (con unión e intersección como unión y encuentro, respectivamente). ^[8]

Para una descripción general de nociones más sólidas de distributividad que son apropiadas para redes completas y que se utilizan para definir clases más especiales de redes, como marcos y redes completamente distributivas , consulte distributividad en la teoría del orden .

Para algunas aplicaciones, la condición de distributividad es demasiado fuerte, y la siguiente propiedad más débil suele ser útil. Una red es modular si, para todos los elementos, se cumple la siguiente identidad: ( Identidad modular ) Esta condición es equivalente al siguiente axioma: implica ( Ley modular ) Una red es modular si y solo si no tiene una subred isomorfa a N ₅ (mostrada en la Fig. 11). ^[7] Además de las redes distributivas, ejemplos de redes modulares son la red de submódulos de un módulo (por lo tanto modular ), la red de ideales bilaterales de un anillo y la red de subgrupos normales de un grupo . El conjunto de términos de primer orden con el ordenamiento "es más específico que" es una red no modular utilizada en el razonamiento automatizado .${\displaystyle (L,\vee ,\wedge )}$${\displaystyle a,b,c\in L,}$${\displaystyle (a\wedge c)\vee (b\wedge c)=((a\wedge c)\vee b)\wedge c.}$
${\displaystyle a\leq c}$${\displaystyle a\vee (b\wedge c)=(a\vee b)\wedge c.}$

Una red finita es modular si y solo si es semimodular tanto superior como inferior . Para una red graduada, la semimodularidad (superior) es equivalente a la siguiente condición en la función de rango${\displaystyle r\colon }$

${\displaystyle r(x)+r(y)\geq r(x\wedge y)+r(x\vee y).}$

Otra condición equivalente (para redes graduadas) es la condición de Birkhoff :

para cada uno y en si y ambos cubren entonces cubre ambos y${\displaystyle x}$${\displaystyle y}$${\displaystyle L,}$${\displaystyle x}$${\displaystyle y}$${\displaystyle x\wedge y,}$${\displaystyle x\vee y}$${\displaystyle x}$${\displaystyle y.}$

Una red se denomina semimodular inferior si su dual es semimodular. Para redes finitas esto significa que las condiciones anteriores se cumplen con y intercambiadas, "cubre" intercambiado con "está cubierto por", y las desigualdades se invierten. ^[9]${\displaystyle \vee }$${\displaystyle \wedge }$

En la teoría de dominios , es natural buscar aproximar los elementos en un orden parcial mediante elementos "mucho más simples". Esto conduce a la clase de conjuntos parciales continuos , que consisten en conjuntos parciales donde cada elemento puede obtenerse como el supremo de un conjunto dirigido de elementos que están muy por debajo del elemento. Si uno puede restringirlos adicionalmente a los elementos compactos de un conjunto parcial para obtener estos conjuntos dirigidos, entonces el conjunto parcial es incluso algebraico . Ambos conceptos pueden aplicarse a los retículos de la siguiente manera:

• Una red continua es una red completa que es continua como un conjunto poset.
• Una red algebraica es una red completa que es algebraica como un conjunto parcial.

Ambas clases tienen propiedades interesantes. Por ejemplo, las redes continuas se pueden caracterizar como estructuras algebraicas (con operaciones infinitarias) que satisfacen ciertas identidades. Si bien no se conoce tal caracterización para las redes algebraicas, se las puede describir "sintácticamente" a través de los sistemas de información de Scott .

Sea una red acotada con el mayor elemento 1 y el menor elemento 0. Dos elementos y de son complementarios entre sí si y solo si:${\displaystyle L}$${\displaystyle x}$${\displaystyle y}$${\displaystyle L}$$${\displaystyle x\vee y=1\quad {\text{ and }}\quad x\wedge y=0.}$$

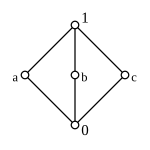
En general, algunos elementos de una red acotada pueden no tener un complemento, y otros pueden tener más de un complemento. Por ejemplo, el conjunto con su ordenamiento habitual es una red acotada y no tiene un complemento. En la red acotada N ₅ , el elemento tiene dos complementos, a saber, y (ver Figura 11). Una red acotada para la que cada elemento tiene un complemento se llama red complementada .${\displaystyle \{0,1/2,1\}}$${\displaystyle {\tfrac {1}{2}}}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

Un retículo complementado que también es distributivo es un álgebra de Boole . Para un retículo distributivo, el complemento de cuando existe es único.${\displaystyle x,}$

En el caso de que el complemento sea único, escribimos y equivalentemente, La operación unaria correspondiente sobre llamada complementación, introduce un análogo de la negación lógica en la teoría de celosía.${\textstyle \lnot x=y}$${\textstyle \lnot y=x.}$${\displaystyle L,}$

Las álgebras de Heyting son un ejemplo de retículos distributivos en los que algunos miembros pueden carecer de complementos. Por otra parte, cada elemento de un álgebra de Heyting tiene un pseudocomplemento , también denotado El pseudocomplemento es el elemento más grande tal que Si el pseudocomplemento de cada elemento de un álgebra de Heyting es de hecho un complemento, entonces el álgebra de Heyting es de hecho un álgebra de Boole.${\displaystyle z}$${\textstyle \lnot x.}$${\displaystyle y}$${\displaystyle x\wedge y=0.}$

Una cadena de a es un conjunto donde la longitud de esta cadena es n , o uno menos que su número de elementos. Una cadena es máxima si cubre todos los${\displaystyle x_{0}}$${\displaystyle x_{n}}$${\displaystyle \left\{x_{0},x_{1},\ldots ,x_{n}\right\},}$${\displaystyle x_{0}<x_{1}<x_{2}<\ldots <x_{n}.}$${\displaystyle x_{i}}$${\displaystyle x_{i-1}}$${\displaystyle 1\leq i\leq n.}$

Si para cualquier par, y donde todas las cadenas máximas de a tienen la misma longitud, entonces se dice que la red satisface la condición de cadena de Jordan-Dedekind .${\displaystyle x}$${\displaystyle y,}$${\displaystyle x<y,}$${\displaystyle x}$${\displaystyle y}$

Una red se llama graduada , a veces clasificada (pero vea Conjunto ordenado por rangos para un significado alternativo), si se puede equipar con una función de rango a veces a , compatible con el ordenamiento (por lo tanto, siempre que ) tal que siempre que cubra entonces El valor de la función de rango para un elemento de red se llama su rango .${\displaystyle (L,\leq )}$ ${\displaystyle r:L\to \mathbb {N} }$${\displaystyle \mathbb {Z} }$${\displaystyle r(x)<r(y)}$${\displaystyle x<y}$${\displaystyle y}$ ${\displaystyle x,}$${\displaystyle r(y)=r(x)+1.}$

Se dice que un elemento de red cubre otro elemento si pero no existe un tal que Aquí, significa y${\displaystyle y}$${\displaystyle x,}$${\displaystyle y>x,}$${\displaystyle z}$${\displaystyle y>z>x.}$${\displaystyle y>x}$${\displaystyle x\leq y}$${\displaystyle x\neq y.}$

Cualquier conjunto puede utilizarse para generar la semirretícula libre La semirretícula libre se define como compuesta por todos los subconjuntos finitos de con la operación de semirretícula dada por la unión de conjuntos ordinaria . La semirretícula libre tiene la propiedad universal . Para la red libre sobre un conjunto, Whitman dio una construcción basada en polinomios sobre los miembros de . ^{[10] [11]}${\displaystyle X}$ ${\displaystyle FX.}$${\displaystyle X,}$${\displaystyle X,}$ ${\displaystyle X}$

Definiremos ahora algunas nociones de orden teórico de importancia para la teoría de retículos. A continuación, un elemento de un retículo se denomina:${\displaystyle x}$${\displaystyle L.}$ ${\displaystyle x}$

• Unir irreducible si implica para todo Si tiene un elemento inferior algunos autores requieren . ^[12] Cuando la primera condición se generaliza a uniones arbitrarias se llama unir completamente irreducible (o -irreducible). La noción dual es irreducibilidad de encuentro ( -irreducible). Por ejemplo, en la Fig. 2, los elementos 2, 3, 4 y 5 son irreducibles de encuentro, mientras que 12, 15, 20 y 30 son irreducibles de encuentro. Dependiendo de la definición, el elemento inferior 1 y el elemento superior 60 pueden o no considerarse irreducibles de encuentro e irreducibles de encuentro, respectivamente. En la red de números reales con el orden usual, cada elemento es irreducible de encuentro, pero ninguno es completamente irreducible de encuentro.${\displaystyle x=a\vee b}$${\displaystyle x=a{\text{ or }}x=b.}$${\displaystyle a,b\in L.}$${\displaystyle L}$${\displaystyle 0,}$${\displaystyle x\neq 0}$${\displaystyle \bigvee _{i\in I}a_{i},}$ ${\displaystyle x}$${\displaystyle \vee }$${\displaystyle \wedge }$
• Unir primo si implica De nuevo algunos autores requieren , aunque esto es inusual. ^[13] Esto también se puede generalizar para obtener la noción completamente unir primo . La noción dual es encuentro primo . Cada elemento de encuentro primo también es encuentro irreducible, y cada elemento de encuentro primo también es encuentro irreducible. Lo inverso se cumple si es distributivo.${\displaystyle x\leq a\vee b}$${\displaystyle x\leq a{\text{ or }}x\leq b.}$${\displaystyle x\neq 0}$${\displaystyle L}$

Sea 0 el elemento inferior. Un elemento de es un átomo si y no existe ningún elemento tal que Entonces se llama:${\displaystyle L}$${\displaystyle x}$${\displaystyle L}$${\displaystyle 0<x}$${\displaystyle y\in L}$${\displaystyle 0<y<x.}$${\displaystyle L}$

• Atómico si por cada elemento distinto de cero existe un átomo de tal que ^[14]${\displaystyle x}$${\displaystyle L,}$${\displaystyle a}$${\displaystyle L}$${\displaystyle a\leq x;}$
• Atomístico si cada elemento es un supremo de átomos. ^[15]${\displaystyle L}$

Sin embargo, muchas fuentes y comunidades matemáticas utilizan el término "atómico" para significar "atomista" como se define anteriormente. ^{[ cita requerida ]}

Las nociones de ideales y la noción dual de filtros se refieren a tipos particulares de subconjuntos de un conjunto parcialmente ordenado y, por lo tanto, son importantes para la teoría de retículos. Se pueden encontrar detalles en las entradas respectivas.

• Unirse y encontrarse  : concepto en la teoría del orden
• Mapa de retículas  – Concepto en matemáticas
• Red ortocomplementada
• Orden total  – Orden cuyos elementos son todos comparables
• Ideal  – Subconjunto no vacío, acotado superiormente y cerrado hacia abajo y filtro (nociones duales)
• Red oblicua  : estructura algebraica Pages displaying wikidata descriptions as a fallback(generalización a uniones y encuentros no conmutativos)
• Red euleriana
• Red de Post  : red de todos los clones (conjuntos de conectivos lógicos cerrados bajo composición y que contienen todas las proyecciones) en un conjunto de dos elementos {0, 1}, ordenados por inclusiónPages displaying wikidata descriptions as a fallback
• Rejilla de Tamari  : objeto matemático formado por un orden en la forma de poner entre paréntesis una expresiónPages displaying wikidata descriptions as a fallback
• Red de Young-Fibonacci
• 0,1-red simple

This article is in list format but may read better as prose. You can help by converting this article, if appropriate. Editing help is available. (March 2017)

Tenga en cuenta que en muchas aplicaciones los conjuntos son solo redes parciales: no todos los pares de elementos tienen un punto de encuentro o unión.

• Topología sin sentido
• Red de subgrupos
• Espacio espectral
• Subespacio invariante
• Operador de cierre
• Interpretación abstracta
• Red de subsunción
• Teoría de conjuntos difusos
• Algebrizaciones de la lógica de primer orden
• Semántica de los lenguajes de programación
• Teoría de dominios
• Ontología (ciencia informática)
• Herencia múltiple
• Análisis de conceptos formales y Lattice Miner (teoría y herramienta)
• Filtro Bloom
• Flujo de información
• Optimización ordinal
• Lógica cuántica
• Gráfica de mediana
• Espacio de conocimiento
• Aprendizaje regular de idiomas
• Modelado analógico