Rotación

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Rotación» – noticias  · periódicos  · libros  · académico  · JSTOR ( marzo de 2014 ) ( Aprenda cómo y cuándo eliminar este mensaje )

La rotación o movimiento rotacional es el movimiento circular de un objeto alrededor de una línea central, conocida como eje de rotación . Una figura plana puede rotar en sentido horario o antihorario alrededor de un eje perpendicular que interseca cualquier parte dentro o fuera de la figura en un centro de rotación . Una figura sólida tiene un número infinito de posibles ejes y ángulos de rotación , incluida la rotación caótica (entre orientaciones arbitrarias ), en contraste con la rotación alrededor de un eje fijo .

El caso particular de una rotación con un eje interno que pasa por el centro de masas del propio cuerpo se conoce como espín (o autorrotación ). ^[1] En ese caso, la intersección de la superficie del eje de espín interno puede llamarse polo ; por ejemplo, la rotación de la Tierra define los polos geográficos . Una rotación alrededor de un eje completamente externo al cuerpo en movimiento se llama revolución (u órbita ), por ejemplo, la órbita de la Tierra alrededor del Sol . Los extremos del eje de revolución externo pueden llamarse polos orbitales . ^[1]

Cada tipo de rotación está involucrado en un tipo correspondiente de velocidad angular (velocidad angular de espín y velocidad angular orbital) y momento angular (momento angular de espín y momento angular orbital).

Matemáticamente , una rotación es un movimiento de un cuerpo rígido que, a diferencia de una traslación , mantiene fijo al menos un punto. Esta definición se aplica a rotaciones en dos dimensiones (en un plano), en las que se mantiene fijo exactamente un punto; y también en tres dimensiones (en el espacio), en las que se pueden mantener fijos puntos adicionales (como en la rotación alrededor de un eje fijo, como una línea infinita).

Todos los movimientos de un cuerpo rígido son rotaciones, traslaciones o combinaciones de ambas.

Una rotación es simplemente una orientación radial progresiva hacia un punto común. Ese punto común se encuentra dentro del eje de ese movimiento. El eje es perpendicular al plano del movimiento.

Si a una rotación alrededor de un punto o eje le sigue una segunda rotación alrededor del mismo punto/eje, se obtiene una tercera rotación. El reverso ( inverso ) de una rotación también es una rotación. Por lo tanto, las rotaciones alrededor de un punto/eje forman un grupo . Sin embargo, una rotación alrededor de un punto o eje y una rotación alrededor de un punto/eje diferente pueden tener como resultado algo distinto a una rotación, por ejemplo, una traslación.

Las rotaciones alrededor de los ejes x , y y z se denominan rotaciones principales . La rotación alrededor de cualquier eje se puede realizar tomando una rotación alrededor del eje x , seguida de una rotación alrededor del eje y , y seguida de una rotación alrededor del eje z . Es decir, cualquier rotación espacial se puede descomponer en una combinación de rotaciones principales.

La combinación de cualquier secuencia de rotaciones de un objeto en tres dimensiones alrededor de un punto fijo es siempre equivalente a una rotación alrededor de un eje (que puede considerarse como una rotación en el plano perpendicular a ese eje). De manera similar, la velocidad de rotación de un objeto en tres dimensiones en cualquier instante es alrededor de algún eje, aunque este eje puede cambiar con el tiempo.

En otras dimensiones que no sean tres, no tiene sentido describir una rotación como si se tratara de un eje, ya que se puede mantener fijo más de un eje a través del objeto; en cambio, las rotaciones simples se describen como si se tratara de un plano. En cuatro o más dimensiones, una combinación de dos o más rotaciones en torno a un plano no es, en general, una rotación en un solo plano.

Las rotaciones bidimensionales, a diferencia de las tridimensionales, no tienen eje de rotación, sino solo un punto alrededor del cual se produce la rotación. Esto equivale, para las transformaciones lineales, a decir que no hay dirección en el plano que se mantenga invariable mediante una rotación bidimensional, excepto, por supuesto, la identidad.

La cuestión de la existencia de dicha dirección es la cuestión de la existencia de un vector propio para la matriz A que representa la rotación. Toda rotación 2D alrededor del origen a través de un ángulo en sentido antihorario se puede representar de forma bastante sencilla mediante la siguiente matriz :${\estilo de visualización \theta}$

${\displaystyle A={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$

Una determinación estándar del valor propio conduce a la ecuación característica

${\displaystyle \lambda ^{2}-2\lambda \cos \theta +1=0,}$

que tiene

${\displaystyle \cos \theta \pm i\sin \theta}$

como sus valores propios. Por lo tanto, no hay ningún valor propio real siempre que , lo que significa que ningún vector real en el plano se mantiene inalterado por A .${\displaystyle \cos \theta \neq \pm 1}$

Sabiendo que la traza es invariante, el ángulo de rotación para una matriz de rotación ortogonal adecuada de 3×3 se encuentra mediante${\estilo de visualización \alpha}$${\estilo de visualización A}$

${\displaystyle \alpha =\cos ^{-1}\left({\frac {A_{11}+A_{22}+A_{33}-1}{2}}\right)}$

Utilizando el arcocoseno principal, esta fórmula da un ángulo de rotación que satisface . El eje de rotación correspondiente debe definirse para apuntar en una dirección que limite el ángulo de rotación a no exceder los 180 grados. (Esto siempre se puede hacer porque cualquier rotación de más de 180 grados sobre un eje siempre se puede escribir como una rotación que tiene si el eje se reemplaza con ).${\displaystyle 0\leq \alpha \leq 180^{\circ }}$${\estilo de visualización m}$${\displaystyle 0\leq \alpha \leq 180^{\circ }}$${\estilo de visualización n=-m}$

Toda rotación propia en el espacio 3D tiene un eje de rotación, que se define de modo que cualquier vector que esté alineado con el eje de rotación no se verá afectado por la rotación. En consecuencia, , y el eje de rotación corresponde, por tanto, a un vector propio de la matriz de rotación asociada a un valor propio de 1. Mientras el ángulo de rotación sea distinto de cero (es decir, la rotación no sea el tensor identidad), existe una y solo una de esas direcciones. Debido a que A solo tiene componentes reales, existe al menos un valor propio real, y los dos valores propios restantes deben ser conjugados complejos entre sí (véase Valores propios y vectores propios#Valores propios y el polinomio característico ). Sabiendo que 1 es un valor propio, se deduce que los dos valores propios restantes son conjugados complejos entre sí, pero esto no implica que sean complejos: podrían ser reales con doble multiplicidad. En el caso degenerado de un ángulo de rotación , los dos valores propios restantes son ambos iguales a −1. En el caso degenerado de un ángulo de rotación cero, la matriz de rotación es la identidad y los tres valores propios son 1 (que es el único caso para el cual el eje de rotación es arbitrario).${\estilo de visualización A}$${\estilo de visualización v}$${\displaystyle Av=v}$${\estilo de visualización \alpha}$${\displaystyle \alpha = 180^{\circ}}$

No se requiere un análisis espectral para encontrar el eje de rotación. Si denota el vector propio unitario alineado con el eje de rotación, y si denota el ángulo de rotación, entonces se puede demostrar que . En consecuencia, el gasto de un análisis de valores propios se puede evitar simplemente normalizando este vector si tiene una magnitud distinta de cero. Por otro lado, si este vector tiene una magnitud cero, significa que . En otras palabras, este vector será cero si y solo si el ángulo de rotación es 0 o 180 grados, y el eje de rotación se puede asignar en este caso normalizando cualquier columna de que tenga una magnitud distinta de cero. ^[2]${\estilo de visualización n}$${\estilo de visualización \alpha}$${\displaystyle 2\sin(\alpha )n=\{A_{32}-A_{23},A_{13}-A_{31},A_{21}-A_{12}\}}$${\displaystyle \sin(\alpha )=0}$${\estilo de visualización A+I}$

Esta discusión se aplica a una rotación propia, y por lo tanto . Cualquier matriz ortogonal impropia de 3x3 puede escribirse como , en la que es ortogonal propia. Es decir, cualquier matriz ortogonal impropia de 3x3 puede descomponerse como una rotación propia (a partir de la cual se puede encontrar un eje de rotación como se describió anteriormente) seguida de una inversión (multiplicación por −1). De ello se deduce que el eje de rotación de es también el vector propio de correspondiente a un valor propio de −1.${\displaystyle \det A=1}$${\displaystyle B}$${\displaystyle B=-A}$${\displaystyle A}$${\displaystyle A}$${\displaystyle B}$

Así como toda rotación tridimensional tiene un eje de rotación, también toda rotación tridimensional tiene un plano, que es perpendicular al eje de rotación y que la rotación deja invariable. La rotación, restringida a este plano, es una rotación 2D ordinaria.

La prueba se desarrolla de manera similar a la discusión anterior. Primero, supongamos que todos los valores propios de la matriz de rotación 3D A son reales. Esto significa que existe una base ortogonal, formada por los vectores propios correspondientes (que son necesariamente ortogonales), sobre la cual el efecto de la matriz de rotación es simplemente estirarla. Si escribimos A en esta base, es diagonal; pero una matriz ortogonal diagonal está formada únicamente por +1 y -1 en las entradas diagonales. Por lo tanto, no tenemos una rotación propiamente dicha, sino la identidad o el resultado de una secuencia de reflexiones.

De ello se deduce, entonces, que una rotación propia tiene algún valor propio complejo. Sea v el vector propio correspondiente. Entonces, como mostramos en el tema anterior, es también un vector propio, y y son tales que su producto escalar se anula:${\displaystyle {\bar {v}}}$${\displaystyle v+{\bar {v}}}$${\displaystyle i(v-{\bar {v}})}$

${\displaystyle i(v^{\text{T}}+{\bar {v}}^{\text{T}})(v-{\bar {v}})=i(v^{\text{T}}v-{\bar {v}}^{\text{T}}{\bar {v}}+{\bar {v}}^{\text{T}}v-v^{\text{T}}{\bar {v}})=0}$

porque, dado que es real, es igual a su conjugado complejo , y y son ambas representaciones del mismo producto escalar entre y .${\displaystyle {\bar {v}}^{\text{T}}{\bar {v}}}$${\displaystyle v^{\text{T}}v}$${\displaystyle {\bar {v}}^{\text{T}}v}$${\displaystyle v^{\text{T}}{\bar {v}}}$${\displaystyle v}$${\displaystyle {\bar {v}}}$

Esto significa que y son vectores ortogonales. Además, ambos son vectores reales por construcción. Estos vectores abarcan el mismo subespacio que y , que es un subespacio invariante bajo la aplicación de A . Por lo tanto, abarcan un plano invariante.${\displaystyle v+{\bar {v}}}$${\displaystyle i(v-{\bar {v}})}$${\displaystyle v}$${\displaystyle {\bar {v}}}$

Este plano es ortogonal al eje invariante, que corresponde al vector propio restante de A , con valor propio 1, debido a la ortogonalidad de los vectores propios de A .

Se dice que un vector está rotando si cambia su orientación. Este efecto generalmente solo se acompaña cuando su vector de tasa de cambio tiene un componente perpendicular distinto de cero al vector original. Esto se puede demostrar considerando un vector que está parametrizado por alguna variable para la cual:${\displaystyle {\vec {A}}}$${\textstyle t}$

${\displaystyle {d|{\vec {A}}|^{2} \over dt}={d({\vec {A}}\cdot {\vec {A}}) \over dt}\Rightarrow {d|{\vec {A}}| \over dt}={d{\vec {A}} \over dt}\cdot {\hat {A}}}$

Lo que también da una relación de tasa de cambio del vector unitario al tomar , como tal vector: mostrando que el vector es perpendicular al vector, . ^[3]${\displaystyle {\vec {A}}}$$${\displaystyle {d{\hat {A}} \over dt}\cdot {\hat {A}}=0}$$${\textstyle {d{\hat {A}} \over dt}}$${\displaystyle {\vec {A}}}$

De:

${\displaystyle {d{\vec {A}} \over dt}={d(|{\vec {A}}|{\hat {A}}) \over dt}={d|{\vec {A}}| \over dt}{\hat {A}}+|{\vec {A}}|\left({d{\hat {A}} \over dt}\right)}$,

Como el primer término es paralelo a él y el segundo es perpendicular a él, podemos concluir en general que los componentes paralelos y perpendiculares de la tasa de cambio de un vector influyen independientemente solo en la magnitud u orientación del vector respectivamente. Por lo tanto, un vector rotatorio siempre tiene un componente perpendicular distinto de cero de su vector de tasa de cambio contra el vector mismo.${\displaystyle {\vec {A}}}$

A medida que aumentan las dimensiones, aumenta el número de vectores de rotación . A lo largo de un espacio de cuatro dimensiones (un hipervolumen ), se producen rotaciones a lo largo de los ejes x, y, z y w. Un objeto rotado sobre un eje w se cruza a través de varios volúmenes , donde cada intersección es igual a un volumen autónomo en un ángulo. Esto da lugar a un nuevo eje de rotación en un hipervolumen de 4 dimensiones, donde un objeto de 3 dimensiones puede rotarse perpendicularmente al eje z. ^{[4] [5]}

La velocidad de rotación se expresa mediante la frecuencia angular (rad/s) o frecuencia ( vueltas por tiempo), o período (segundos, días, etc.). La tasa de cambio de la frecuencia angular en función del tiempo es la aceleración angular (rad/s ² ), causada por el par motor . La relación entre el par motor y la aceleración angular se expresa mediante el momento de inercia .

El vector de velocidad angular (un vector axial ) también describe la dirección del eje de rotación. De manera similar, el par es un vector axial.

La física de la rotación alrededor de un eje fijo se describe matemáticamente con la representación eje-ángulo de las rotaciones. Según la regla de la mano derecha , la dirección que se aleja del observador se asocia con la rotación en el sentido de las agujas del reloj y la dirección que se acerca al observador con la rotación en el sentido contrario de las agujas del reloj, como un tornillo .

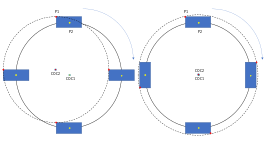
Es posible que los objetos tengan trayectorias circulares periódicas sin cambiar su orientación . Estos tipos de movimiento se tratan como movimiento circular en lugar de rotación, más específicamente como una traslación curvilínea. Dado que la traslación implica el desplazamiento de cuerpos rígidos mientras se conserva la orientación del cuerpo, en el caso de la traslación curvilínea, todos los puntos tienen la misma velocidad instantánea, mientras que el movimiento relativo solo se puede observar en movimientos que involucran rotación. ^[6]

En la rotación, la orientación del objeto cambia y el cambio de orientación es independiente de los observadores cuyos marcos de referencia tienen una orientación relativa constante a lo largo del tiempo. Por el teorema de Euler , cualquier cambio de orientación puede describirse por rotación sobre un eje a través de un punto de referencia elegido. ^[6] Por lo tanto, la distinción entre rotación y movimiento circular puede hacerse requiriendo un eje instantáneo para la rotación, una línea que pasa por el centro instantáneo del círculo y es perpendicular al plano de movimiento . En el ejemplo que representa la traslación curvilínea, el centro de los círculos para el movimiento se encuentra en una línea recta pero es paralela al plano de movimiento y, por lo tanto, no se resuelve en un eje de rotación. Por el contrario, un cuerpo giratorio siempre tendrá su eje instantáneo de velocidad cero, perpendicular al plano de movimiento. ^[7]

De manera más general, debido al teorema de Chasles , cualquier movimiento de cuerpos rígidos puede tratarse como una composición de rotación y traslación , llamado movimiento plano general. ^[6] Un ejemplo simple de rotación pura se considera en la rotación alrededor de un eje fijo .

Actualmente se cree que las leyes de la física son invariables bajo cualquier rotación fija (aunque parecen cambiar cuando se las observa desde un punto de vista rotatorio: véase marco de referencia rotatorio ).

En la cosmología física moderna, el principio cosmológico es la noción de que la distribución de la materia en el universo es homogénea e isótropa cuando se observa en una escala suficientemente grande, ya que se espera que las fuerzas actúen uniformemente en todo el universo y no tengan una dirección preferida, y, por lo tanto, no deberían producir irregularidades observables en la estructuración a gran escala a lo largo de la evolución del campo de materia que fue establecido inicialmente por el Big Bang.

En particular, para un sistema que se comporta de la misma manera independientemente de cómo esté orientado en el espacio, su Lagrangiano es rotacionalmente invariante . Según el teorema de Noether , si la acción (la integral en el tiempo de su Lagrangiano) de un sistema físico es invariante bajo rotación, entonces el momento angular se conserva .

Las rotaciones de Euler proporcionan una descripción alternativa de una rotación. Es una composición de tres rotaciones definidas como el movimiento obtenido al cambiar uno de los ángulos de Euler mientras se dejan los otros dos constantes. Las rotaciones de Euler nunca se expresan en términos del marco externo, o en términos del marco del cuerpo rotado que se mueve conjuntamente, sino en una mezcla. Constituyen un sistema de ejes de rotación mixtos, donde el primer ángulo mueve la línea de nodos alrededor del eje externo z , el segundo gira alrededor de la línea de nodos y el tercero es una rotación intrínseca alrededor de un eje fijo en el cuerpo que se mueve.

Estas rotaciones se denominan precesión , nutación y rotación intrínseca .

En astronomía , la rotación es un fenómeno comúnmente observado; incluye tanto el giro (autorrotación) como la revolución orbital.

Las estrellas , los planetas y otros cuerpos similares pueden girar sobre sus ejes. La velocidad de rotación de los planetas del sistema solar se midió por primera vez mediante el seguimiento de características visuales. La rotación estelar se mide a través del efecto Doppler o mediante el seguimiento de características activas de la superficie. Un ejemplo son las manchas solares , que giran alrededor del Sol a la misma velocidad que los gases externos que lo forman.

En determinadas circunstancias, los cuerpos en órbita pueden bloquear su rotación con respecto a su rotación orbital alrededor de un cuerpo más grande. Este efecto se denomina bloqueo de marea ; la Luna está bloqueada por marea con respecto a la Tierra.

Esta rotación induce una aceleración centrífuga en el sistema de referencia de la Tierra que contrarresta ligeramente el efecto de la gravitación cuanto más cerca se está del ecuador . La gravedad de la Tierra combina ambos efectos de masa, de modo que un objeto pesa ligeramente menos en el ecuador que en los polos. Otra razón es que con el tiempo la Tierra se deforma ligeramente hasta convertirse en un esferoide achatado ; un abultamiento ecuatorial similar se desarrolla en otros planetas.

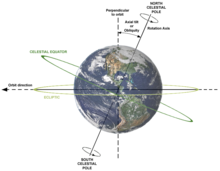
Otra consecuencia de la rotación de un planeta son los fenómenos de precesión y nutación . Al igual que en un giroscopio , el efecto general es un ligero "bamboleo" en el movimiento del eje de un planeta. Actualmente, la inclinación del eje de la Tierra respecto de su plano orbital ( oblicuidad de la eclíptica ) es de 23,44 grados, pero este ángulo cambia lentamente (a lo largo de miles de años). (Véase también Precesión de los equinoccios y Estrella Polar .)

Aunque revolución se utiliza a menudo como sinónimo de rotación , en muchos campos, en particular la astronomía y campos relacionados, revolución , a menudo denominada revolución orbital para mayor claridad, se utiliza cuando un cuerpo se mueve alrededor de otro mientras que rotación se utiliza para significar el movimiento alrededor de un eje. Las lunas giran alrededor de sus planetas, los planetas giran alrededor de sus estrellas (como la Tierra alrededor del Sol); y las estrellas giran lentamente alrededor de sus centros galácticos . El movimiento de los componentes de las galaxias es complejo, pero generalmente incluye un componente de rotación.

La mayoría de los planetas del Sistema Solar , incluida la Tierra , giran en la misma dirección en la que orbitan alrededor del Sol . Las excepciones son Venus y Urano . Se puede pensar que Venus gira lentamente hacia atrás (o que está "al revés"). Urano gira casi de lado en relación con su órbita. La especulación actual es que Urano comenzó con una orientación prograda típica y fue golpeado de lado por un gran impacto al principio de su historia. El planeta enano Plutón (antes considerado un planeta) es anómalo en varios sentidos, incluido el hecho de que también gira de lado.

En dinámica de vuelo , las rotaciones principales descritas con los ángulos de Euler se conocen como cabeceo , alabeo y guiñada . El término rotación también se utiliza en aviación para referirse al cabeceo hacia arriba (el morro se mueve hacia arriba) de una aeronave, en particular al iniciar el ascenso después del despegue.

Las rotaciones principales tienen la ventaja de modelar una serie de sistemas físicos, como los cardanes y los joysticks , por lo que se visualizan fácilmente y son una forma muy compacta de almacenar una rotación. Pero son difíciles de usar en los cálculos, ya que incluso las operaciones simples, como la combinación de rotaciones, son costosas de realizar y sufren una forma de bloqueo del cardán donde los ángulos no se pueden calcular de forma única para ciertas rotaciones.

Muchas atracciones de feria proporcionan rotación. Una noria tiene un eje central horizontal y ejes paralelos para cada góndola, donde la rotación es opuesta, por gravedad o mecánicamente. Como resultado, en cualquier momento la orientación de la góndola es vertical (no rotada), solo trasladada. La punta del vector de traslación describe un círculo. Un carrusel proporciona rotación sobre un eje vertical. Muchas atracciones proporcionan una combinación de rotaciones sobre varios ejes. En Chair-O-Planes, la rotación sobre el eje vertical se proporciona mecánicamente, mientras que la rotación sobre el eje horizontal se debe a la fuerza centrípeta . En las inversiones de montaña rusa, la rotación sobre el eje horizontal es uno o más ciclos completos, donde la inercia mantiene a las personas en sus asientos.

La rotación de una pelota u otro objeto, generalmente llamada giro , juega un papel en muchos deportes, incluidos el topspin y el backspin en el tenis , el inglés , el follow y draw en el billar y el pool , las bolas curvas en el béisbol , los bolos con giro en el cricket , los deportes de disco volador , etc. Las palas de tenis de mesa se fabrican con diferentes características de superficie para permitir al jugador impartir una mayor o menor cantidad de giro a la pelota.

La rotación de un jugador una o más veces alrededor de un eje vertical puede llamarse giro en patinaje artístico , giro (del bastón o del ejecutante) en giro de bastón , o 360 , 540 , 720 , etc. en snowboard , etc. La rotación de un jugador o ejecutante una o más veces alrededor de un eje horizontal puede llamarse flip , roll , somersault , heli , etc. en gimnasia , esquí acuático o muchos otros deportes, o uno y medio , dos y medio , gainer (comenzando de espaldas al agua), etc. en buceo , etc. Una combinación de rotación vertical y horizontal (voltereta hacia atrás con 360°) se llama möbius en salto estilo libre de esquí acuático .

La rotación de un jugador sobre un eje vertical, generalmente entre 180 y 360 grados, puede denominarse movimiento de giro y se utiliza como maniobra engañosa o de evasión, o en un intento de jugar, pasar o recibir una pelota o un disco, etc., o para permitirle a un jugador ver la portería o a otros jugadores. Se ve a menudo en hockey , baloncesto , fútbol de varios tipos, tenis , etc.

• "Rotación", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Producto de rotaciones en cut-the-knot . cut-the-knot.org
• Cuando un triángulo es equilátero en cut-the-knot.cut-the-knot.org
• Rotar puntos usando coordenadas polares, howtoproperly.com
• Rotación en dos dimensiones por Sergio Aníbal Mejía después del trabajo de Roger Germundsson y Entendiendo la rotación 3D por Roger Germundsson, Wolfram Demonstrations Project .demonstrations.wolfram.com
• Rotación, reflexión y cambio de marco: tensores ortogonales en la mecánica de ingeniería computacional, IOP Publishing