Álgebra geométrica
En matemáticas , un álgebra geométrica (también conocida como álgebra de Clifford ) es un álgebra que puede representar y manipular objetos geométricos como vectores . El álgebra geométrica se construye a partir de dos operaciones fundamentales, la suma y el producto geométrico. La multiplicación de vectores da como resultado objetos de dimensiones superiores llamados multivectores . En comparación con otros formalismos para manipular objetos geométricos, el álgebra geométrica es notable por admitir la división de vectores (aunque generalmente no por todos los elementos) y la suma de objetos de diferentes dimensiones.
El producto geométrico fue mencionado brevemente por primera vez por Hermann Grassmann , [1] quien estaba principalmente interesado en desarrollar el álgebra exterior estrechamente relacionada . En 1878, William Kingdon Clifford amplió en gran medida el trabajo de Grassmann para formar lo que ahora se denominan habitualmente álgebras de Clifford en su honor (aunque el propio Clifford eligió llamarlas "álgebras geométricas"). Clifford definió el álgebra de Clifford y su producto como una unificación del álgebra de Grassmann y el álgebra de cuaterniones de Hamilton . Agregar el dual del producto exterior de Grassmann (el "encuentro") permite el uso del álgebra de Grassmann-Cayley , y una versión conforme de esta última junto con un álgebra conforme de Clifford produce un álgebra geométrica conforme (CGA) que proporciona un marco para las geometrías clásicas . [2] En la práctica, estas y varias operaciones derivadas permiten una correspondencia de elementos, subespacios y operaciones del álgebra con interpretaciones geométricas. Durante varias décadas, las álgebras geométricas fueron ignoradas, eclipsadas en gran medida por el cálculo vectorial , recién desarrollado para describir el electromagnetismo. El término "álgebra geométrica" fue popularizado nuevamente en la década de 1960 por David Hestenes , quien defendió su importancia para la física relativista. [3]
Los escalares y vectores tienen su interpretación habitual y forman subespacios distintos de un álgebra geométrica. Los bivectores proporcionan una representación más natural de las cantidades pseudovectoriales del cálculo vectorial 3D que se derivan como un producto vectorial , como el área orientada, el ángulo de rotación orientado, el par, el momento angular y el campo magnético . Un trivector puede representar un volumen orientado, etc. Se puede utilizar un elemento llamado cuchilla para representar un subespacio y proyecciones ortogonales sobre ese subespacio. Las rotaciones y las reflexiones se representan como elementos. A diferencia de un álgebra vectorial, un álgebra geométrica acomoda naturalmente cualquier número de dimensiones y cualquier forma cuadrática, como en la relatividad .
Ejemplos de álgebras geométricas aplicadas en física incluyen el álgebra del espacio-tiempo (y el álgebra menos común del espacio físico ) y el álgebra geométrica conforme . El cálculo geométrico , una extensión del AG que incorpora diferenciación e integración , se puede utilizar para formular otras teorías como el análisis complejo y la geometría diferencial , por ejemplo, utilizando el álgebra de Clifford en lugar de formas diferenciales . El álgebra geométrica ha sido defendida, sobre todo por David Hestenes [4] y Chris Doran [5] , como el marco matemático preferido para la física . Los defensores afirman que proporciona descripciones compactas e intuitivas en muchas áreas, incluidas la mecánica clásica y cuántica , la teoría electromagnética y la relatividad . [6] El AG también ha encontrado uso como herramienta computacional en gráficos de computadora [7] y robótica .
Definición y notación
Hay varias formas diferentes de definir un álgebra geométrica. El enfoque original de Hestenes era axiomático, [8] "lleno de significado geométrico" y equivalente al álgebra universal [a] de Clifford. [9] Dado un espacio vectorial de dimensión finita sobre un cuerpo con una forma bilineal simétrica (el producto interno , [b] por ejemplo, la métrica euclidiana o lorentziana ) , el álgebra geométrica del espacio cuadrático es el álgebra de Clifford , un elemento del cual se llama multivector. El álgebra de Clifford se define comúnmente como un álgebra cociente del álgebra tensorial , aunque esta definición es abstracta, por lo que la siguiente definición se presenta sin requerir álgebra abstracta .
- Definición
- Un álgebra asociativa unitaria con una forma bilineal simétrica no degenerada es el álgebra de Clifford del espacio cuadrático si [ 10]
- contiene y como subespacios distintos
- para
- genera como un álgebra
- no es generado por ningún subespacio propio de .
Para cubrir formas bilineales simétricas degeneradas, se debe modificar la última condición. [c] Se puede demostrar que estas condiciones caracterizan de manera única al producto geométrico.
En el resto de este artículo, solo se considerará el caso real , . La notación (respectivamente ) se utilizará para denotar un álgebra geométrica para la cual la forma bilineal tiene la signatura (respectivamente ).
El producto en el álgebra se llama producto geométrico , y el producto en el álgebra exterior contenida se llama producto exterior (frecuentemente llamado producto cuña o producto externo [d] ). Es estándar denotar estos respectivamente por yuxtaposición (es decir, suprimiendo cualquier símbolo de multiplicación explícito) y el símbolo .
La definición anterior del álgebra geométrica es todavía algo abstracta, por lo que resumiremos aquí las propiedades del producto geométrico. Para multivectores :
- ( cierre )
- , donde es el elemento identidad (existencia de un elemento identidad )
- ( asociatividad )
- y ( distributividad )
- para .
El producto exterior tiene las mismas propiedades, excepto que la última propiedad anterior se reemplaza por por .
Nótese que en la última propiedad anterior, el número real no necesita ser no negativo si no es positivo-definido. Una propiedad importante del producto geométrico es la existencia de elementos que tienen un inverso multiplicativo. Para un vector , si entonces existe y es igual a . Un elemento distinto de cero del álgebra no necesariamente tiene un inverso multiplicativo. Por ejemplo, si es un vector en tal que , el elemento es tanto un elemento idempotente no trivial como un divisor de cero distinto de cero , y por lo tanto no tiene inverso. [e]
Es habitual identificar y con sus imágenes bajo las incrustaciones naturales y . En este artículo, se asume esta identificación. En todo momento, los términos escalar y vector se refieren a elementos de y respectivamente (y de sus imágenes bajo esta incrustación).
Producto geométrico

Para los vectores y , podemos escribir el producto geométrico de dos vectores cualesquiera y como la suma de un producto simétrico y un producto antisimétrico:
Así podemos definir el producto interno de los vectores como
de modo que el producto simétrico se puede escribir como
Por el contrario, está completamente determinado por el álgebra. La parte antisimétrica es el producto exterior de los dos vectores, el producto del álgebra exterior contenida :
Luego por simple adición:
- la forma no generalizada o vectorial del producto geométrico.
Los productos internos y externos están asociados con conceptos familiares del álgebra vectorial estándar. Geométricamente, y son paralelos si su producto geométrico es igual a su producto interno, mientras que y son perpendiculares si su producto geométrico es igual a su producto externo. En un álgebra geométrica para la cual el cuadrado de cualquier vector distinto de cero es positivo, el producto interno de dos vectores puede identificarse con el producto escalar del álgebra vectorial estándar. El producto externo de dos vectores puede identificarse con el área con signo encerrada por un paralelogramo cuyos lados son los vectores. El producto vectorial de dos vectores en dimensiones con forma cuadrática definida positiva está estrechamente relacionado con su producto externo.
La mayoría de los casos de álgebras geométricas de interés tienen una forma cuadrática no degenerada. Si la forma cuadrática es completamente degenerada , el producto interno de dos vectores cualesquiera siempre es cero, y el álgebra geométrica es entonces simplemente un álgebra exterior. A menos que se indique lo contrario, este artículo tratará únicamente álgebras geométricas no degeneradas.
El producto exterior se extiende naturalmente como un operador binario bilineal asociativo entre dos elementos cualesquiera del álgebra, satisfaciendo las identidades
donde la suma es sobre todas las permutaciones de los índices, con el signo de la permutación , y son vectores (no elementos generales del álgebra). Como cada elemento del álgebra puede expresarse como la suma de productos de esta forma, esto define el producto exterior para cada par de elementos del álgebra. De la definición se deduce que el producto exterior forma un álgebra alternada .
La ecuación de estructura equivalente para el álgebra de Clifford es [16] [17]
donde es el Pfaffian de y proporciona combinaciones , , de índices divididos en y partes y es la paridad de la combinación .
El Pfaffian proporciona una métrica para el álgebra exterior y, como señaló Claude Chevalley, el álgebra de Clifford se reduce al álgebra exterior con una forma cuadrática cero. [18] El papel que juega el Pfaffian se puede entender desde un punto de vista geométrico desarrollando el álgebra de Clifford a partir de los símplices . [19] Esta derivación proporciona una mejor conexión entre el triángulo de Pascal y los símplices porque proporciona una interpretación de la primera columna de unos.
Cuchillas, calidades y bases
Un multivector que es el producto exterior de vectores linealmente independientes se llama cuchilla , y se dice que es de grado . [f] Un multivector que es la suma de cuchillas de grado se llama multivector (homogéneo) de grado . A partir de los axiomas, con clausura, todo multivector del álgebra geométrica es una suma de cuchillas.
Consideremos un conjunto de vectores linealmente independientes que abarcan un subespacio -dimensional del espacio vectorial. Con ellos, podemos definir una matriz simétrica real (de la misma manera que una matriz de Gram ).
Por el teorema espectral , se puede diagonalizar a una matriz diagonal mediante una matriz ortogonal mediante
Definir un nuevo conjunto de vectores , conocidos como vectores base ortogonales, que serán aquellos transformados por la matriz ortogonal:
Como las transformaciones ortogonales conservan los productos internos, se deduce que y, por lo tanto, son perpendiculares. En otras palabras, el producto geométrico de dos vectores distintos está completamente especificado por su producto exterior o, de manera más general,
Por lo tanto, cada hoja de grado puede escribirse como el producto exterior de vectores. De manera más general, si se permite un álgebra geométrica degenerada, entonces la matriz ortogonal se reemplaza por una matriz de bloques que es ortogonal en el bloque no degenerado, y la matriz diagonal tiene entradas de valor cero a lo largo de las dimensiones degeneradas. Si los nuevos vectores del subespacio no degenerado se normalizan de acuerdo con
entonces estos vectores normalizados deben elevar al cuadrado a o . Por la ley de inercia de Sylvester , el número total de y el número total de a lo largo de la matriz diagonal es invariante. Por extensión, el número total de estos vectores que elevan al cuadrado a y el número total que elevan al cuadrado a es invariante. (El número total de vectores base que elevan al cuadrado a cero también es invariante, y puede ser distinto de cero si se permite el caso degenerado). Denotamos esta álgebra . Por ejemplo, modela el espacio euclidiano tridimensional , el espacio-tiempo relativista y un álgebra geométrica conforme de un espacio tridimensional.
El conjunto de todos los productos posibles de vectores base ortogonales con índices en orden creciente, incluido el producto vacío, forma una base para toda el álgebra geométrica (un análogo del teorema PBW ). Por ejemplo, la siguiente es una base para el álgebra geométrica :
Una base formada de esta manera se denomina base estándar para el álgebra geométrica, y cualquier otra base ortogonal para producirá otra base estándar. Cada base estándar consta de elementos. Cada multivector del álgebra geométrica se puede expresar como una combinación lineal de los elementos de la base estándar. Si los elementos de la base estándar son un conjunto de índices, entonces el producto geométrico de dos multivectores cualesquiera es
La terminología " -vector" se utiliza a menudo para describir multivectores que contienen elementos de un solo grado. En el espacio de dimensiones superiores, algunos de estos multivectores no son cuchillas (no se pueden factorizar en el producto exterior de vectores). A modo de ejemplo, en no se puede factorizar ; sin embargo, normalmente, estos elementos del álgebra no se prestan a la interpretación geométrica como objetos, aunque pueden representar cantidades geométricas como rotaciones. Solo los - , - , - y -vectores son siempre cuchillas en el -espacio .
Versor
Un -versor es un multivector que puede expresarse como el producto geométrico de vectores invertibles. [g] [21] Los cuaterniones unitarios (originalmente llamados versores por Hamilton) pueden identificarse con rotores en el espacio 3D de la misma manera que los rotores 2D reales subsumen números complejos; para los detalles, consulte a Dorst. [22]
Algunos autores utilizan el término "producto versor" para referirse al caso frecuente en el que un operando está "emparedado" entre operadores. Las descripciones de rotaciones y reflexiones, incluidos sus morfismos externos, son ejemplos de este tipo de emparedado. Estos morfismos externos tienen una forma algebraica particularmente simple. [h] En concreto, una aplicación de vectores de la forma
- se extiende al morfismo externo
Dado que tanto los operadores como el operando son versores, existe la posibilidad de ejemplos alternativos, como rotar un rotor o reflejar un espinor, siempre que se pueda atribuir algún significado geométrico o físico a dichas operaciones.
Por el teorema de Cartan-Dieudonné tenemos que toda isometría puede darse como reflexiones en hiperplanos y como las reflexiones compuestas proporcionan rotaciones entonces tenemos que las transformaciones ortogonales son versores.
En términos de grupo, para un real, no degenerado , habiendo identificado el grupo como el grupo de todos los elementos invertibles de , Lundholm da una prueba de que el "grupo versor" (el conjunto de versores invertibles) es igual al grupo de Lipschitz ( también conocido como grupo de Clifford, aunque Lundholm desaprueba este uso). [23]
Subgrupos del grupo Lipschitz
Denotamos la involución de grado como y la reversión como .
Aunque el grupo de Lipschitz (definido como ) y el grupo versor (definido como ) tienen definiciones divergentes, son el mismo grupo. Lundholm define los subgrupos , y del grupo de Lipschitz. [24]
| Subgrupo | Definición | Término GA |
|---|---|---|
| Versores | ||
| Versores de unidad | ||
| Versores de unidad uniforme | ||
| Rotores |
Múltiples análisis de espinores utilizan AG como representación. [25]
Proyección de calificaciones
Se puede establecer una estructura de espacio vectorial graduado en un álgebra geométrica mediante el uso del producto exterior que es naturalmente inducido por el producto geométrico.
Dado que el producto geométrico y el producto exterior son iguales en los vectores ortogonales, esta clasificación se puede construir convenientemente utilizando una base ortogonal .
Los elementos del álgebra geométrica que son múltiplos escalares de son de grado y se llaman escalares . Los elementos que están en el lapso de son de grado y son los vectores ordinarios. Los elementos en el lapso de son de grado y son los bivectores. Esta terminología continúa hasta el último grado de -vectores. Alternativamente, -vectores se llaman pseudoescalares , -vectores se llaman pseudovectores, etc. Muchos de los elementos del álgebra no se califican mediante este esquema ya que son sumas de elementos de diferente grado. Se dice que dichos elementos son de grado mixto . La calificación de multivectores es independiente de la base elegida originalmente.
Esta es una gradación como espacio vectorial, pero no como álgebra. Debido a que el producto de una -cuchilla y una -cuchilla está contenido en el espacio de -cuchillas , el álgebra geométrica es un álgebra filtrada .
Un multivector se puede descomponer con el operador de proyección de grado , que genera la porción de grado de . Como resultado:
A modo de ejemplo, el producto geométrico de dos vectores ya que y y , para otros que y .
Un multivector también puede descomponerse en componentes par e impar, que pueden expresarse respectivamente como la suma de los componentes de grado par y de grado impar anteriores:
Este es el resultado de olvidar la estructura de un espacio vectorial graduado a un espacio vectorial graduado . El producto geométrico respeta esta gradación más gruesa . Por lo tanto , además de ser un espacio vectorial graduado , el álgebra geométrica es un álgebra graduada , también conocida como superálgebra .
Restringiéndonos a la parte par, el producto de dos elementos pares también es par. Esto significa que los multivectores pares definen una subálgebra par . La subálgebra par de un álgebra geométrica de dimensión es isomorfa (sin preservar ni la filtración ni la gradación) a un álgebra geométrica completa de dimensiones. Algunos ejemplos incluyen y .
Representación de subespacios
El álgebra geométrica representa los subespacios de como aspas, y por eso coexisten en la misma álgebra con vectores de . Un subespacio -dimensional de se representa tomando una base ortogonal y usando el producto geométrico para formar la aspa . Hay múltiples aspas que representan ; todas las que representan son múltiplos escalares de . Estas aspas se pueden separar en dos conjuntos: múltiplos positivos de y múltiplos negativos de . Se dice que los múltiplos positivos de tienen la misma orientación que , y los múltiplos negativos la orientación opuesta .
Las hojas son importantes ya que las operaciones geométricas como proyecciones, rotaciones y reflexiones dependen de la factorabilidad a través del producto exterior que (la clase restringida de) -hojas proporcionan pero que (la clase generalizada de) multivectores de grado no proporcionan cuando .
Unidades pseudoescalares
Los pseudoescalares unitarios son cuchillas que desempeñan papeles importantes en GA. Un pseudoescalar unitario para un subespacio no degenerado de es una cuchilla que es el producto de los miembros de una base ortonormal para . Se puede demostrar que si y son ambos pseudoescalares unitarios para , entonces y . Si uno no elige una base ortonormal para , entonces la incrustación de Plücker da un vector en el álgebra exterior pero solo hasta la escala. Usando el isomorfismo del espacio vectorial entre el álgebra geométrica y el álgebra exterior, esto da la clase de equivalencia de para todo . La ortonormalidad elimina esta ambigüedad excepto por los signos anteriores.
Supongamos que se forma el álgebra geométrica con el conocido producto interno definido positivo en . Dado un plano (subespacio bidimensional) de , se puede encontrar una base ortonormal que abarca el plano, y así encontrar un pseudoescalar unitario que represente este plano. El producto geométrico de dos vectores cualesquiera en el espacio de y se encuentra en , es decir, es la suma de un -vector y un -vector.
Por las propiedades del producto geométrico, . La semejanza con la unidad imaginaria no es incidental: el subespacio es -álgebra isomorfa a los números complejos . De esta manera, una copia de los números complejos está incrustada en el álgebra geométrica para cada subespacio bidimensional de en el que la forma cuadrática está definida.
A veces es posible identificar la presencia de una unidad imaginaria en una ecuación física. Dichas unidades surgen de una de las muchas cantidades del álgebra real que se elevan al cuadrado a , y tienen importancia geométrica debido a las propiedades del álgebra y la interacción de sus diversos subespacios.
En , se produce otro caso familiar. Dada una base estándar que consiste en vectores ortonormales de , el conjunto de todos los -vectores está abarcado por
Al etiquetarlos como , y (desviándonos momentáneamente de nuestra convención de mayúsculas), el subespacio generado por -vectores y -vectores es exactamente . Se ve que este conjunto es la subálgebra par de , y además es isomorfo como -álgebra a los cuaterniones , otro sistema algebraico importante.
Ampliaciones de los productos interiores y exteriores.
Es una práctica común extender el producto exterior de los vectores a toda el álgebra. Esto se puede hacer mediante el uso del operador de proyección de grados mencionado anteriormente:
- (el producto exterior )
Esta generalización es coherente con la definición anterior que implica antisimetrización. Otra generalización relacionada con el producto exterior es el producto conmutador:
- (el producto del conmutador )
El producto regresivo es el dual del producto exterior (que corresponde respectivamente a "encuentro" y "unión" en este contexto). [i] La especificación dual de elementos permite, para las hojas y , la intersección (o encuentro) donde se debe tomar la dualidad en relación con una hoja que contiene tanto a como a (la hoja más pequeña de este tipo es la unión). [27]
con la unidad pseudoescalar del álgebra. El producto regresivo, como el producto exterior, es asociativo. [28]
El producto interno de vectores también se puede generalizar, pero de más de una forma no equivalente. El artículo (Dorst 2002) ofrece un tratamiento completo de varios productos internos diferentes desarrollados para álgebras geométricas y sus interrelaciones, y la notación se toma de allí. Muchos autores utilizan el mismo símbolo que para el producto interno de vectores para su extensión elegida (por ejemplo, Hestenes y Perwass). No ha surgido una notación consistente.
Entre estas diferentes generalizaciones del producto interno sobre vectores se encuentran:
- (la contracción de la izquierda )
- (la contracción correcta )
- (el producto escalar )
- (el producto "punto (gordo)") [j]
Dorst (2002) argumenta que es preferible utilizar contracciones en lugar del producto interno de Hestenes; son algebraicamente más regulares y tienen interpretaciones geométricas más claras. Varias identidades que incorporan las contracciones son válidas sin restricción de sus entradas. Por ejemplo,
Los beneficios de usar la contracción por la izquierda como una extensión del producto interno en vectores incluyen que la identidad se extiende a para cualquier vector y multivector , y que la operación de proyección se extiende a para cualquier hoja y cualquier multivector (con una modificación menor para acomodar nulo , que se muestra a continuación).
Doble base
Sea una base de , es decir, un conjunto de vectores linealmente independientes que abarcan el espacio vectorial de dimensión . La base que es dual a es el conjunto de elementos del espacio vectorial dual que forma un sistema biortogonal con esta base, siendo así que los elementos denotados satisfacen
¿Dónde está el delta de Kronecker ?
Dada una forma cuadrática no degenerada en , se identifica naturalmente con , y la base dual puede considerarse como elementos de , pero en general no son el mismo conjunto que la base original.
Dado además un GA de , sea
sea el pseudoescalar (que no necesariamente es cuadrado de ) formado a partir de la base . Los vectores de base duales pueden construirse como
donde denota que el ésimo vector base se omite del producto.
Una base dual también se conoce como base recíproca o marco recíproco.
Un uso importante de una base dual es separar vectores en componentes. Dado un vector , los componentes escalares se pueden definir como
en términos de los cuales se pueden separar en componentes vectoriales como
También podemos definir componentes escalares como
en términos de los cuales se pueden separar en componentes vectoriales en términos de la base dual como
Una base dual como la definida anteriormente para el subespacio vectorial de un álgebra geométrica se puede extender para cubrir todo el álgebra. [29] Para que sea más compacto, usaremos una sola letra mayúscula para representar un conjunto ordenado de índices vectoriales. Es decir, escribir
donde , podemos escribir una hoja base como
La hoja recíproca correspondiente tiene los índices en orden opuesto:
De manera similar al caso anterior con los vectores, se puede demostrar que
¿Dónde está el producto escalar?
Con un multivector, podemos definir componentes escalares como [30]
en términos de los cuales se pueden separar en cuchillas componentes como
Alternativamente podemos definir componentes escalares
en términos de los cuales se pueden separar en cuchillas componentes como
Funciones lineales
Aunque es más fácil trabajar con un versor porque se puede representar directamente en el álgebra como un multivector, los versores son un subgrupo de funciones lineales sobre multivectores, que aún se pueden usar cuando sea necesario. El álgebra geométrica de un espacio vectorial -dimensional está abarcado por una base de elementos. Si un multivector se representa por una matriz columna real de coeficientes de una base del álgebra, entonces todas las transformaciones lineales del multivector se pueden expresar como la multiplicación de matrices por una matriz real. Sin embargo, una transformación lineal tan general permite intercambios arbitrarios entre grados, como una "rotación" de un escalar en un vector, que no tiene una interpretación geométrica evidente.
Es de interés una transformación lineal general de vectores a vectores. Con la restricción natural de preservar el álgebra exterior inducida, el externalmorfismo de la transformación lineal es la única extensión [k] del versor. Si es una función lineal que asigna vectores a vectores, entonces su externalmorfismo es la función que obedece la regla
para una cuchilla, extendida a todo el álgebra a través de la linealidad.
Modelado de geometrías
Aunque se ha prestado mucha atención a CGA, cabe señalar que GA no es solo un álgebra, sino una de una familia de álgebras con la misma estructura esencial. [31]
Modelo de espacio vectorial
El subálgebra par de es isomorfa a los números complejos , como se puede ver al escribir un vector en términos de sus componentes en una base ortonormal y multiplicar por el vector base , obteniéndose
donde nos identificamos desde
De manera similar, el subálgebra par de con base es isomorfa a los cuaterniones como se puede ver identificando , y .
Toda álgebra asociativa tiene una representación matricial; reemplazando los tres vectores base cartesianos por las matrices de Pauli se obtiene una representación de :
Poniendo los puntos sobre el « vector de Pauli » (una díada ):
- con vectores arbitrarios y y multiplicando por se obtiene:
- (De manera equivalente, por inspección, )
Modelo espacio-temporal
En física, las principales aplicaciones son el álgebra geométrica del espacio-tiempo de Minkowski 3+1 , , llamada álgebra del espacio-tiempo (STA), [3] o menos comúnmente, , interpretada como álgebra del espacio físico (APS).
Mientras que en STA los puntos del espacio-tiempo se representan simplemente por vectores, en APS los puntos del espacio-tiempo -dimensional se representan en cambio por paravectores , un vector tridimensional (espacio) más un escalar unidimensional (tiempo).
En el álgebra del espacio-tiempo, el tensor del campo electromagnético tiene una representación bivectorial . [32] Aquí, es el pseudoescalar unitario (o elemento de volumen de cuatro dimensiones), es el vector unitario en la dirección del tiempo, y y son los vectores clásicos del campo eléctrico y magnético (con un componente de tiempo cero). Usando la corriente de cuatro corrientes , las ecuaciones de Maxwell se convierten entonces en
Formulación Ecuaciones homogéneas Ecuaciones no homogéneas Campos Potenciales (de cualquier calibre) Potenciales (calibre de Lorenz)
En cálculo geométrico, la yuxtaposición de vectores como en indica el producto geométrico y se puede descomponer en partes como . Aquí está la derivada del covector en cualquier espacio-tiempo y se reduce a en el espacio-tiempo plano. Donde juega un papel en el espacio - tiempo de Minkowski , que es sinónimo del papel de en el espacio - tiempo euclidiano y está relacionado con el d'Alembertiano por . De hecho, dado un observador representado por un vector temporal que apunta al futuro, tenemos
Los impulsos en este espacio métrico lorentziano tienen la misma expresión que la rotación en el espacio euclidiano, donde es el bivector generado por las direcciones de tiempo y espacio involucradas, mientras que en el caso euclidiano es el bivector generado por las dos direcciones del espacio, lo que refuerza la "analogía" hasta casi la identidad.
Las matrices de Dirac son una representación de , mostrando la equivalencia con las representaciones matriciales utilizadas por los físicos.
Modelos homogéneos
Los modelos homogéneos generalmente se refieren a una representación proyectiva en la que los elementos de los subespacios unidimensionales de un espacio vectorial representan puntos de una geometría.
En un álgebra geométrica de un espacio de dimensiones, los rotores representan un conjunto de transformaciones con grados de libertad, correspondientes a rotaciones – por ejemplo, cuando y cuando . El álgebra geométrica se utiliza a menudo para modelar un espacio proyectivo , es decir, como un modelo homogéneo : un punto, una línea, un plano, etc. se representa mediante una clase de equivalencia de elementos del álgebra que difieren por un factor escalar invertible.
Los rotores en un espacio de dimensión tienen grados de libertad, los mismos que el número de grados de libertad en las rotaciones y traslaciones combinadas para un espacio -dimensional.
Este es el caso del Álgebra Geométrica Proyectiva (PGA), que se utiliza [33] [34] [35] para representar isometrías euclidianas en geometría euclidiana (cubriendo así la gran mayoría de aplicaciones de ingeniería de la geometría). En este modelo, se agrega una dimensión degenerada a las tres dimensiones euclidianas para formar el álgebra . Con una identificación adecuada de subespacios para representar puntos, líneas y planos, los versores de esta álgebra representan todas las isometrías euclidianas propias, que siempre son movimientos de tornillo en el espacio tridimensional, junto con todas las isometrías euclidianas impropias, que incluyen reflexiones, rotorreflexiones, transflexiones y reflexiones puntuales.
PGA se combina con un operador de complemento para obtener fórmulas de unión, encuentro, distancia y ángulo. [36] En efecto, el complemento intercambia los vectores base que están presentes y ausentes en la expresión de cada término de la representación algebraica. Por ejemplo, en el PGA o espacio tridimensional, el complemento de la línea es la línea , porque y son elementos base que no están contenidos en pero están contenidos en . En el PGA del espacio bidimensional, el complemento de es , ya que no hay ningún elemento.
PGA es un sistema ampliamente utilizado que combina el álgebra geométrica con representaciones homogéneas en geometría, pero existen otros sistemas similares. El modelo conforme que se analiza a continuación es homogéneo, al igual que el "Álgebra geométrica cónica" [37] ; véase Álgebra geométrica basada en el plano para un análisis de los modelos homogéneos de geometría elíptica e hiperbólica en comparación con la geometría euclidiana derivada de PGA.
Modelo conforme

Al trabajar dentro de GA, el espacio euclidiano (junto con un punto conforme en el infinito) se integra de manera proyectiva en el CGA a través de la identificación de puntos euclidianos con subespacios 1D en el cono nulo 4D del subespacio vectorial CGA 5D. Esto permite que todas las transformaciones conformes se realicen como rotaciones y reflexiones y es covariante , extendiendo las relaciones de incidencia de la geometría proyectiva a objetos redondos como círculos y esferas.
En concreto, añadimos vectores base ortogonales y tales que y a la base del espacio vectorial que genera e identifica vectores nulos.
- como el punto en el origen y
- como un punto conforme en el infinito (ver Compactificación ), dando
(Algunos autores establecen y . [36] ) Este procedimiento tiene algunas similitudes con el procedimiento para trabajar con coordenadas homogéneas en geometría proyectiva, y en este caso permite modelar transformaciones euclidianas de como transformaciones ortogonales de un subconjunto de .
La CGA, un área de la AG que cambia rápidamente y es fluida, también se está investigando para aplicaciones a la física relativista.
Tabla de modelos
Nótese en esta lista que y se pueden intercambiar y se aplica el mismo nombre; por ejemplo, con relativamente pocos cambios, consulte la convención de signos . Por ejemplo, y se conocen como Álgebra del espacio-tiempo. [38]
| Nombre | Firma | Cuchillas, por ejemplo, objetos geométricos orientados que el álgebra puede representar. | Rotores, por ejemplo, transformaciones que preservan la orientación y que el álgebra puede representar. | Notas |
|---|---|---|---|---|
| Espacio vectorial GA, VGA | Planos y rectas que pasan por el origen | Rotaciones, p. ej. | Primer GA descubierto [¿ por quién? ] | |
| AG proyectivo, PGA, AG rígido, RGA, AG basado en planos | Planos, líneas y puntos en cualquier lugar del espacio. | Rotaciones y traslaciones, por ejemplo, movimientos rígidos , también conocidos como | Las ligeras modificaciones de la firma permiten modelar el espacio hiperbólico y elíptico (véase el artículo principal). No se puede modelar todo el grupo "proyectivo". | |
| Álgebra del espacio-tiempo , STA | Volúmenes, planos y líneas a través del origen en el espacio-tiempo | Rotaciones y aumentos del espacio-tiempo, por ejemplo , el grupo de Lorentz | Base de la teoría de calibre Gravedad . | |
| Álgebra del espacio-tiempo proyectivizada, [39] STAP | Volúmenes, planos, líneas y puntos (eventos) en el espacio-tiempo | Rotaciones, traslaciones y aumentos del espacio-tiempo ( grupo de Poincaré ) | ||
| GA conforme , CGA | Esferas, círculos, pares de puntos (o dipolos), puntos redondos, puntos planos, líneas y planos en cualquier lugar del espacio. | Transformaciones del espacio que preservan ángulos ( Grupo conforme ) | ||
| Álgebra espaciotemporal conforme, [40] CSTA | Esferas, círculos, planos, líneas, conos de luz, trayectorias de objetos con aceleración constante, todo en el espacio-tiempo. | Transformaciones conformes del espacio-tiempo, por ejemplo, transformaciones que preservan la rapidez a lo largo de longitudes de arco a través del espacio-tiempo. | Relacionado con la teoría de Twistor . | |
| Álgebra madre [41] | Desconocido | Grupo proyectivo | ||
| GA para cónicas, GAC AG 2D conforme cuadrático QC2GA [42] [37] | Puntos, par/triple/cuádruple de puntos, Cónica, Lápiz de hasta 6 cónicas independientes. | Reflexiones, traslaciones, rotaciones, dilataciones, otras | Se pueden crear cónicas a partir de puntos de control y lápices de cónicas. | |
| AG Conforme Cuádrico, QCGA [43] | Puntos, tuplas de hasta 8 puntos, superficies cuádricas, cónicas, cónicas sobre superficies cuadráticas (como Cónica esférica ), lápices de hasta 9 superficies cuádricas. | Reflexiones, traslaciones, rotaciones, dilataciones, otras | Se pueden crear superficies cuadráticas a partir de puntos de control y se pueden determinar sus normales de superficie. | |
| Álgebra geométrica doblemente conforme (DCGA) [44] | Puntos, ciclos de Darboux, superficies cuádricas | Reflexiones, traslaciones, rotaciones, dilataciones, otras | Utiliza bivectores de dos bases CGA independientes para representar "matrices" simétricas de 5×5 de 15 coeficientes únicos. Esto se hace a costa de la capacidad de realizar intersecciones y construcciones por puntos. |
Interpretación geométrica en el modelo del espacio vectorial
Proyección y rechazo
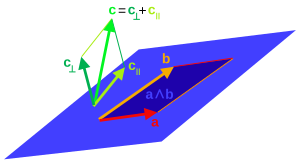
Para cualquier vector y cualquier vector invertible ,
donde la proyección de sobre (o la parte paralela) es
y el rechazo de desde (o la parte ortogonal) es
Usando el concepto de una -cuchilla como representación de un subespacio de y cada multivector siendo expresado en última instancia en términos de vectores, esto se generaliza a la proyección de un multivector general sobre cualquier -cuchilla invertible como [ l ]
con el rechazo definido como
La proyección y el rechazo se generalizan a cuchillas nulas al reemplazar la inversa con la pseudoinversa con respecto al producto contractivo. [m] El resultado de la proyección coincide en ambos casos para cuchillas no nulas. [45] [46] Para cuchillas nulas , se debe usar la definición de la proyección dada aquí con la primera contracción en lugar de la segunda sobre la pseudoinversa, [n] ya que solo entonces el resultado está necesariamente en el subespacio representado por . [45] La proyección se generaliza a través de la linealidad a multivectores generales . [o] La proyección no es lineal en y no se generaliza a objetos que no sean cuchillas.
Reflexión
Las reflexiones simples en un hiperplano se expresan fácilmente en el álgebra mediante la conjugación con un único vector. Estas sirven para generar el grupo de rotaciones y reflexiones generales .
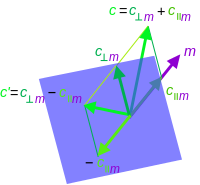
La reflexión de un vector a lo largo de un vector , o equivalentemente en el hiperplano ortogonal a , es lo mismo que negar la componente de un vector paralelo a . El resultado de la reflexión será
Esta no es la operación más general que puede considerarse como una reflexión cuando la dimensión . Una reflexión general puede expresarse como la composición de cualquier número impar de reflexiones de un solo eje. Por lo tanto, una reflexión general de un vector puede escribirse
dónde
- y
Si definimos la reflexión a lo largo de un vector no nulo del producto de vectores como la reflexión de cada vector en el producto a lo largo del mismo vector, obtenemos para cualquier producto de un número impar de vectores que, a modo de ejemplo,
y para el producto de un número par de vectores que
Utilizando el concepto de que cada multivector se expresa en última instancia en términos de vectores, la reflexión de un multivector general que utiliza cualquier versor de reflexión puede escribirse
donde es el automorfismo de reflexión a través del origen del espacio vectorial ( ) extendido a través de la linealidad a todo el álgebra.
Rotaciones
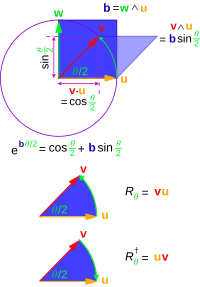
Si tenemos un producto de vectores entonces denotamos el inverso como
A modo de ejemplo, supongamos que obtenemos
Escalando de manera que entonces
Por lo tanto , la longitud de no cambia. También podemos demostrar que
Por lo tanto, la transformación conserva tanto la longitud como el ángulo. Por lo tanto, se puede identificar como una rotación o una rotorreflexión; se denomina rotor si es una rotación propia (como lo es si se puede expresar como un producto de un número par de vectores) y es una instancia de lo que se conoce en AG como un versor .
Existe un método general para rotar un vector que implica la formación de un multivector de la forma que produce una rotación en el plano y con la orientación definida por una -cuchilla .
Los rotores son una generalización de los cuaterniones a espacios dimensionales .
Ejemplos y aplicaciones
Hipervolumen de un paralelotopo generado por vectores
Para los vectores y que abarcan un paralelogramo tenemos
con el resultado de que es lineal en el producto de la "altitud" por la "base" del paralelogramo, es decir, su área.
Interpretaciones similares son válidas para cualquier número de vectores que abarcan un paraleletopo de dimensión ; el producto exterior de los vectores , es decir , tiene una magnitud igual al volumen del -paralelotopo. Un -vector no tiene necesariamente la forma de un paraleletopo – esta es una visualización conveniente. Podría tener cualquier forma, aunque el volumen sea igual al del paraleletopo.
Intersección de una recta y un plano

Podemos definir la línea paramétricamente por , donde y son vectores de posición para los puntos P y T y es el vector de dirección de la línea.
Entonces
- y
entonces
y
Sistemas rotatorios
Una cantidad rotacional como el par o el momento angular se describe en álgebra geométrica como un bivector. Supongamos que una trayectoria circular en un plano arbitrario que contiene vectores ortonormales y está parametrizada por un ángulo.
Designando el bivector unitario de este plano como el número imaginario
Este vector de trayectoria se puede escribir convenientemente en forma exponencial compleja.
y la derivada con respecto al ángulo es

Por ejemplo, el par se define generalmente como la magnitud del componente de fuerza perpendicular multiplicado por la distancia, o el trabajo por unidad de ángulo. Por lo tanto, el par, la tasa de cambio del trabajo con respecto al ángulo, debido a una fuerza , es
Las cantidades rotacionales se representan en el cálculo vectorial en tres dimensiones mediante el producto vectorial . Junto con la elección de una forma de volumen orientada , se pueden relacionar con el producto exterior con su interpretación geométrica más natural de tales cantidades como bivectores mediante el uso de la relación dual .
A diferencia de la descripción del par mediante producto vectorial, , la descripción del álgebra geométrica no introduce un vector en la dirección normal; un vector que no existe en dos y que no es único en más de tres dimensiones. El bivector unitario describe el plano y la orientación de la rotación, y el sentido de la rotación es relativo al ángulo entre los vectores y .
Cálculo geométrico
El cálculo geométrico extiende el formalismo para incluir la diferenciación y la integración, incluyendo la geometría diferencial y las formas diferenciales . [47]
Esencialmente, la derivada vectorial se define de modo que la versión GA del teorema de Green sea verdadera,
y luego uno puede escribir
como un producto geométrico, generalizando efectivamente el teorema de Stokes (incluida la versión en forma diferencial del mismo).
En 1D cuando es una curva con puntos finales y , entonces
se reduce a
o el teorema fundamental del cálculo integral.
También se desarrolla el concepto de variedad vectorial y la teoría de integración geométrica (que generaliza las formas diferenciales).
Historia
Antes del siglo XX
Aunque la conexión de la geometría con el álgebra se remonta al menos a los Elementos de Euclides en el siglo III a. C. (véase Álgebra geométrica griega ), la AG en el sentido utilizado en este artículo no se desarrolló hasta 1844, cuando se utilizó de forma sistemática para describir las propiedades geométricas y las transformaciones de un espacio. En ese año, Hermann Grassmann introdujo la idea de un álgebra geométrica con total generalidad como un cierto cálculo (análogo al cálculo proposicional ) que codificaba toda la información geométrica de un espacio. [48] El sistema algebraico de Grassmann podía aplicarse a varios tipos diferentes de espacios, siendo los principales el espacio euclidiano , el espacio afín y el espacio proyectivo . Siguiendo a Grassmann, en 1878 William Kingdon Clifford examinó el sistema algebraico de Grassmann junto con los cuaterniones de William Rowan Hamilton en (Clifford 1878). Desde su punto de vista, los cuaterniones describían ciertas transformaciones (a las que llamó rotores ), mientras que el álgebra de Grassmann describía ciertas propiedades (o Strecken, como longitud, área y volumen). Su contribución fue definir un nuevo producto -el producto geométrico- sobre un álgebra de Grassmann existente, que comprendía que los cuaterniones vivían dentro de esa álgebra. Posteriormente, Rudolf Lipschitz en 1886 generalizó la interpretación de Clifford de los cuaterniones y los aplicó a la geometría de rotaciones en dimensiones. Más tarde, estos desarrollos llevarían a otros matemáticos del siglo XX a formalizar y explorar las propiedades del álgebra de Clifford.
Sin embargo, otro desarrollo revolucionario del siglo XIX eclipsaría por completo las álgebras geométricas: el análisis vectorial , desarrollado independientemente por Josiah Willard Gibbs y Oliver Heaviside . El análisis vectorial estuvo motivado por los estudios de James Clerk Maxwell sobre el electromagnetismo , y específicamente la necesidad de expresar y manipular convenientemente ciertas ecuaciones diferenciales . El análisis vectorial tenía un cierto atractivo intuitivo en comparación con los rigores de las nuevas álgebras. Tanto los físicos como los matemáticos lo adoptaron rápidamente como su conjunto de herramientas geométricas de elección, particularmente después del influyente libro de texto de 1901 Análisis vectorial de Edwin Bidwell Wilson , después de las conferencias de Gibbs.
En más detalle, ha habido tres enfoques para el álgebra geométrica: análisis cuaterniónico , iniciado por Hamilton en 1843 y geometrizado como rotores por Clifford en 1878; álgebra geométrica, iniciada por Grassmann en 1844; y análisis vectorial, desarrollado a partir del análisis cuaterniónico a fines del siglo XIX por Gibbs y Heaviside. El legado del análisis cuaterniónico en el análisis vectorial se puede ver en el uso de , , para indicar los vectores base de : se piensa como los cuaterniones puramente imaginarios. Desde la perspectiva del álgebra geométrica, el subálgebra par del Álgebra del Espacio-Tiempo es isomorfo al AG del espacio euclidiano 3D y los cuaterniones son isomorfos al subálgebra par del AG del espacio euclidiano 3D, lo que unifica los tres enfoques.
Siglo XX y actualidad
El progreso en el estudio de las álgebras de Clifford avanzó silenciosamente durante el siglo XX, aunque en gran parte debido al trabajo de algebristas abstractos como Élie Cartan , Hermann Weyl y Claude Chevalley . El enfoque geométrico de las álgebras geométricas ha visto una serie de resurgimientos en el siglo XX. En matemáticas, el Álgebra geométrica de Emil Artin [49] analiza el álgebra asociada con cada una de varias geometrías, incluyendo la geometría afín , la geometría proyectiva , la geometría simpléctica y la geometría ortogonal . En física, las álgebras geométricas han revivido como una "nueva" forma de hacer mecánica clásica y electromagnetismo, junto con temas más avanzados como la mecánica cuántica y la teoría de gauge. [5] David Hestenes reinterpretó las matrices de Pauli y Dirac como vectores en el espacio ordinario y el espacio-tiempo, respectivamente, y ha sido un defensor contemporáneo principal del uso del álgebra geométrica.
En el campo de los gráficos por ordenador y la robótica, las álgebras geométricas han cobrado vida para representar de forma eficiente las rotaciones y otras transformaciones. Para aplicaciones de AG en robótica ( teoría de tornillos , cinemática y dinámica mediante versores), visión artificial, control y computación neuronal (aprendizaje geométrico), véase Bayro (2010).
Véase también
- Comparación entre el álgebra vectorial y el álgebra geométrica
- Álgebra de Clifford
- Álgebra de Grassmann-Cayley
- Álgebra del espacio-tiempo
- Espinor
- Cuaternio
- Álgebra del espacio físico
- Álgebra geométrica universal
Notas
- ^ Un álgebra "universal" es el álgebra más "completa" o menos degenerada que satisface todas las ecuaciones que la definen. En este artículo, por "álgebra de Clifford" nos referimos al álgebra universal de Clifford.
- ^ El término producto interno tal como se utiliza en álgebra geométrica se refiere a la forma bilineal simétrica en el subespacio vectorial y es sinónimo del producto escalar de un espacio vectorial pseudoeuclidiano , no del producto interno en un espacio vectorial normado. Algunos autores pueden extender el significado de producto interno a toda el álgebra, pero hay poco consenso al respecto. Incluso en textos sobre álgebras geométricas, el término no se utiliza universalmente.
- ^ Puede reemplazarse por la condición de que [11] el producto de cualquier conjunto de vectores linealmente independientes en no debe estar en o que [12] la dimensión del álgebra debe ser .
- ^ El término producto externo utilizado en álgebra geométrica entra en conflicto con el significado de producto externo en otras partes de las matemáticas.
- ^ Dado , tenemos que , mostrando que es idempotente, y que , mostrando que es un divisor de cero distinto de cero.
- ^ Grado es sinónimo de grado de un elemento homogéneo bajo la gradación como álgebra con el producto exterior (una -gradación), y no bajo el producto geométrico.
- ^ "reviviendo y generalizando un tanto un término del cálculo de cuaterniones de Hamilton que ha caído en desuso" Hestenes definió un -versor como un multivector que puede factorizarse en un producto de vectores. [20]
- ^ Sólo los externalmorfismos de las transformaciones lineales que respetan la forma bilineal se ajustan a esta descripción; los externalmorfismos en general no son expresables en términos de operaciones algebraicas.
- ^ [...] la operación de producto exterior y la relación de unión tienen esencialmente el mismo significado. El álgebra de Grassmann-Cayley considera la relación de encuentro como su contraparte y proporciona un marco unificador en el que estas dos operaciones tienen igualdad de condiciones [...] El propio Grassmann definió la operación de encuentro como dual de la operación de producto exterior, pero matemáticos posteriores definieron el operador de encuentro independientemente del producto exterior a través de un proceso llamado shuffle , y la operación de encuentro se denomina producto shuffle . Se muestra que esta es una operación antisimétrica que satisface la asociatividad, definiendo un álgebra por derecho propio. Por lo tanto, el álgebra de Grassmann-Cayley tiene dos estructuras algebraicas simultáneamente: una basada en el producto exterior (o unión), la otra basada en el producto shuffle (o encuentro). De ahí el nombre de "álgebra doble", y se muestra que las dos son duales entre sí. [26]
- ^ Esto no debe confundirse con la generalización irregular de Hestenes , donde la notación distintiva es de Dorst, Fontijne y Mann (2007), pág. 590, §B.1, que señala que los componentes escalares deben manejarse por separado con este producto.
- ^ La condición que generalmente se agrega para garantizar que el mapa cero sea único.
- ^ Esta definición sigue a Dorst, Fontijne y Mann (2007) y Perwass (2009): la contracción izquierda utilizada por Dorst reemplaza el producto interno ("punto grueso") que utiliza Perwass, en consonancia con la restricción de Perwass de que el grado de no puede exceder al de .
- ^ Dorst parece simplemente asumir que , mientras que Perwass (2009) define , donde es el conjugado de , equivalente al reverso de hasta un signo.
- ^ Es decir, la proyección debe definirse como y no como , aunque las dos son equivalentes para hojas no nulas .
- ^ Esta generalización a todos aparentemente no es considerada por Perwass ni Dorst .
Citas
- ^ Hestenes 1986, pág. 6
- ^ Li 2008, pág. 411
- ^ desde Hestenes 1966
- ^ Hestenes 2003
- ^ de Doran 1994
- ^ Lasenby, Lasenby y Doran 2000
- ^ Hildenbrand y otros, 2004
- ^ Hestenes y Sobczyk 1984, pág. 3–5
- ^ Aragón, Aragón y Rodríguez 1997, p. 101
- ^ Lounesto 2001, pág. 190
- ^ Lounesto 2001, pág. 191
- ^ Vaz y da Rocha 2016, pag. 58, Teorema 3.1
- ^ desde Hestenes 2005
- ^ Penrose 2007
- ^ Wheeler, Misner y Thorne 1973, pág. 83
- ^ Wilmot 1988a, pág. 2338
- ^ Wilmot 1988b, pág. 2346
- ^ Valle Chevalley 1991
- ^ Wilmot 2023
- ^ Hestenes y Sobczyk 1984, pág. 103
- ^ Dorst, Fontijne y Mann 2007, pág. 204
- ^ Dorst, Fontijne y Mann 2007, págs. 177-182
- ^ Lundholm y Svensson 2009, págs.58 y siguientes
- ^ Lundholm y Svensson 2009, pág. 58
- ^ Francis y Kosowsky 2008
- ^ Kanatani 2015, págs. 112-113
- ^ Dorst y Lasenby 2011, pág. 443
- ^ Vaz y da Rocha 2016, §2.8
- ^ Hestenes y Sobczyk 1984, pág. 31
- ^ Doran y Lasenby 2003, pág. 102
- ^ Dorst y Lasenby 2011, pág. vi
- ^ Electromagnetismo usando Álgebra Geométrica versus Componentes , consultado el 19 de marzo de 2013
- ^ Selig 2005
- ^ Hadfield y Lasenby 2020
- ^ "Álgebra geométrica proyectiva", projectivegeometricalgebra.org , consultado el 3 de octubre de 2023
- ^ desde Lengyel 2024
- ^ ab Hrdina, Návrat y Vašík 2018
- ^ Wu 2022
- ^ Sókolov 2013
- ^ Lasenby 2004
- ^ Dorst 2016
- ^ Perwass 2009
- ^ Breuils y otros, 2019
- ^ Pascua y Hitzer 2017
- ^ ab Dorst, Fontijne y Mann 2007, §3.6 p. 85
- ^ Perwass 2009, §3.2.10.2 p. 83
- ^ Hestenes y Sobczyk 1984
- ^ Grassman 1844
- ^ Artin 1988
Referencias y lecturas adicionales
- Ordenado cronológicamente
- Grassmann, Hermann (1844), Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, Leipzig: O. Wigand, OCLC 20521674
- Clifford, profesor (1878), "Aplicaciones del álgebra extensiva de Grassmann", American Journal of Mathematics , 1 (4): 350–358, doi :10.2307/2369379, JSTOR 2369379
- Artin, Emil (1988) [1957], Álgebra geométrica , Wiley Classics Library, Wiley, doi :10.1002/9781118164518, ISBN 978-0-471-60839-4, Sr. 1009557
- Hestenes, David (1966), Álgebra espacio-temporal , Gordon y Breach, ISBN 978-0-677-01390-9, OCLC 996371
- Wheeler, JA; Misner, C.; Thorne, KS (1973), Gravitación , WH Freeman, ISBN 978-0-7167-0344-0
- Bourbaki, Nicolas (1980), "Cap. 9 "Algèbres de Clifford"", Elementos de Mathématique. Algèbre , Hermann, ISBN 9782225655166
- Hestenes, David ; Sobczyk, Garret (1984), Álgebra de Clifford para cálculo geométrico, un lenguaje unificado para matemáticas y física , Springer Países Bajos, ISBN 978-90-277-1673-6
- Hestenes, David (1986), "Un lenguaje unificado para las matemáticas y la física", en JSR Chisholm; AK Commons (eds.), Álgebras de Clifford y sus aplicaciones en la física matemática , NATO ASI Series (Serie C), vol. 183, Springer, págs. 1–23, doi :10.1007/978-94-009-4728-3_1, ISBN 978-94-009-4728-3
- Wilmot, GP (1988a), La estructura del álgebra de Clifford. Journal of Mathematical Physics , vol. 29, págs. 2338–2345
- Wilmot, GP (1988b), "Álgebra de Clifford y la expansión de Pfaffian", Journal of Mathematical Physics , 29 : 2346–2350, doi :10.1063/1.528118
- Chevalley, Claude (1991), La teoría algebraica de los espinores y las álgebras de Clifford, Obras completas , vol. 2, Springer, ISBN 3-540-57063-2
- Doran, Chris JL (1994), Álgebra geométrica y su aplicación a la física matemática (tesis doctoral), Universidad de Cambridge , doi : 10.17863/CAM.16148, hdl : 1810/251691, OCLC 53604228
- Baylis, WE, ed. (2011) [1996], Álgebra (geométrica) de Clifford con aplicaciones a la física, las matemáticas y la ingeniería , Birkhäuser , ISBN 9781461241058
- Aragón, G.; Aragón, JL; Rodríguez, MA (1997), "Clifford Algebras and Geométrica Algebra", Avances en Applied Clifford Algebras , 7 (2): 91–102, doi :10.1007/BF03041220, S2CID 120860757
- Hestenes, David (1999), Nuevos fundamentos para la mecánica clásica (2.ª ed.), Springer Verlag, ISBN 978-0-7923-5302-7
- Lasenby, Joan; Lasenby, Anthony N.; Doran, Chris JL (2000), "Un lenguaje matemático unificado para la física y la ingeniería en el siglo XXI" (PDF) , Philosophical Transactions of the Royal Society A , 358 (1765): 21–39, Bibcode :2000RSPTA.358...21L, doi :10.1098/rsta.2000.0517, S2CID 91884543, archivado (PDF) desde el original el 2015-03-19
- Lounesto, Pertti (2001), Álgebras y espinores de Clifford (2.ª ed.), Cambridge University Press , ISBN 978-0-521-00551-7
- Baylis, WE (2002), Electrodinámica: un enfoque geométrico moderno (2.ª ed.), Birkhäuser , ISBN 978-0-8176-4025-5
- Dorst, Leo (2002), "Los productos internos del álgebra geométrica", en Dorst, L.; Doran, C.; Lasenby, J. (eds.), Aplicaciones del álgebra geométrica en la ciencia informática y la ingeniería , Birkhäuser , págs. 35–46, doi :10.1007/978-1-4612-0089-5_2, ISBN 978-1-4612-0089-5
- Doran, Chris JL ; Lasenby, Anthony N. (2003), Álgebra geométrica para físicos (PDF) , Cambridge University Press, ISBN 978-0-521-71595-9, archivado (PDF) del original el 6 de enero de 2009
- Hestenes, David (2003), "Conferencia de la Medalla Oersted 2002: Reformando el lenguaje matemático de la física" (PDF) , Am. J. Phys. , 71 (2): 104–121, Bibcode :2003AmJPh..71..104H, CiteSeerX 10.1.1.649.7506 , doi :10.1119/1.1522700
{{citation}}: CS1 maint: url-status (link) - Hildenbrand, Dietmar; Fontijne, Daniel; Perwass, Christian; Dorst, Leo (2004), "Álgebra geométrica y su aplicación a los gráficos por ordenador" (PDF) , Actas de Eurographics 2004 , doi :10.2312/egt.20041032, archivado (PDF) desde el original el 2015-09-06
- Lasenby, Anthony (2004), "Modelos conformes del espacio de De Sitter, condiciones iniciales para la inflación y el CMB", Actas de la conferencia AIP , vol. 736, págs. 53–70, arXiv : astro-ph/0411579 , doi :10.1063/1.1835174, S2CID 18034896
- Hestenes, David (2005), Introducción a la cartilla para el álgebra geométrica
- Selig, JM (2005), Fundamentos geométricos de la robótica, Monografías en informática, Nueva York, NY: Springer New York, doi : 10.1007/b138859, ISBN 978-0-387-20874-9
- Bain, J. (2006), "Estructuralismo espacio-temporal: §5 Variedades frente a álgebra geométrica", en Dennis Dieks (ed.), La ontología del espacio-tiempo, Elsevier, pág. 54 y siguientes , ISBN 978-0-444-52768-4
- Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007), Álgebra geométrica para informática: un enfoque orientado a objetos para la geometría, Elsevier, ISBN 978-0-12-369465-2, OCLC 132691969
- Penrose, Roger (2007), El camino hacia la realidad , Libros antiguos, ISBN 978-0-679-77631-4
- Francis, Matthew R.; Kosowsky, Arthur (2008), "La construcción de espinores en álgebra geométrica", Anales de Física , 317 (2): 383–409, arXiv : math-ph/0403040v2 , Bibcode :2005AnPhy.317..383F, doi :10.1016/j.aop.2004.11.008, S2CID 119632876
- Li, Hongbo (2008), Álgebras invariantes y razonamiento geométrico, World Scientific, ISBN 9789812770110Capítulo 1 en formato PDF
- Vince, John A. (2008), Álgebra geométrica para gráficos por computadora , Springer, ISBN 978-1-84628-996-5
- Lundholm, Douglas; Svensson, Lars (2009), "Álgebra de Clifford, álgebra geométrica y aplicaciones", arXiv : 0907.5356v1 [math-ph]
- Perwass, Christian (2009), Álgebra geométrica con aplicaciones en ingeniería , Geometría y computación, vol. 4, Bibcode :2009gaae.book.....P, doi :10.1007/978-3-540-89068-3, ISBN 978-3-540-89067-6
- Selig, JM (2000), "Álgebra de Clifford de puntos, líneas y planos" (PDF) , Robotica , 18 (5): 545–556, doi :10.1017/S0263574799002568, S2CID 28929170
- Bayro-Corrochano, Eduardo (2010), Computación geométrica para transformadas wavelet, visión, aprendizaje, control y acción de robots , Springer Verlag, ISBN 9781848829299
- Bayro-Corrochano, E.; Scheuermann, Gerik, eds. (2010), Computación de álgebra geométrica en ingeniería e informática, Springer, ISBN 9781849961080Extracto en línea en https://davidhestenes.net/geocalc/html/UAFCG.html #5 Nuevas herramientas para la geometría computacional y rejuvenecimiento de la teoría de tornillos
- Goldman, Ron (2010), Replanteando los cuaterniones: teoría y computación , Morgan & Claypool, Parte III. Replanteando los cuaterniones y las álgebras de Clifford, ISBN 978-1-60845-420-4
- Dorst, Leo.; Lasenby, Joan (2011), Guía de álgebra geométrica en la práctica , Springer, ISBN 9780857298119
- Macdonald, Alan (2011), Álgebra lineal y geométrica, CreateSpace, ISBN 9781453854938, OCLC 704377582
- Snygg, John (2011), Un nuevo enfoque para la geometría diferencial utilizando el álgebra geométrica de Clifford , Springer, ISBN 978-0-8176-8282-8
- Hildenbrand, Dietmar (2012), "Fundamentos de la computación en álgebra geométrica", Numerical Analysis and Applied Mathematics Icnaam 2012: International Conference of Numerical Analysis and Applied Mathematics , Actas de la conferencia AIP, 1479 (1): 27–30, Bibcode :2012AIPC.1479...27H, doi :10.1063/1.4756054
- Sokolov, Andrey (2013), Álgebra de Clifford y el modelo proyectivo de los espacios de Minkowski (pseudoeuclidianos) , arXiv : 1307.4179
- Bromborsky, Alan (2014), Introducción al álgebra geométrica y al cálculo (PDF) , archivado (PDF) desde el original el 15 de octubre de 2019
- Klawitter, Daniel (2015), Álgebras de Clifford , doi :10.1007/978-3-658-07618-4, ISBN 978-3-658-07617-7
- Kanatani, Kenichi (2015), Comprensión del álgebra geométrica: Hamilton, Grassmann y Clifford para visión artificial y gráficos , CRC Press, ISBN 978-1-4822-5951-3
- Li, Hongbo; Huang, Lei; Shao, Changpeng; Dong, Lei (2015), "Geometría proyectiva tridimensional con álgebra geométrica", arXiv : 1507.06634v1 [math.MG]
- Hestenes, David (2017), "La génesis del álgebra geométrica: una retrospectiva personal", Advances in Applied Clifford Algebras , 27 : 351–379, doi :10.1007/s00006-016-0664-z, S2CID 253592888
- Dorst, Leo (2016), "Geometría proyectiva orientada en 3D a través de versores de ", Avances en álgebras de Clifford aplicadas , 26 (4): 1137–1172, doi : 10.1007/s00006-015-0625-y
- Vaz, Jayme; da Rocha, Roldão (2016), Introducción a las álgebras y espinores de Clifford , Oxford University Press, Bibcode :2016icas.book.....V, ISBN 978-0-19-878292-6
- Easter, Robert Benjamin; Hitzer, Eckhard (2017), "Álgebra geométrica conforme doble", Advances in Applied Clifford Algebras , 27 (3): 2175–2199, doi :10.1007/s00006-017-0784-0, S2CID 253600526
- Du, Juan; Goldman, Ron; Mann, Stephen (2017), "Modelado de geometría 3D en el álgebra de Clifford R(4, 4)", Advances in Applied Clifford Algebras , 27 (4): 3039–3062, doi :10.1007/s00006-017-0798-7, S2CID 253587390
- Bayro-Corrochano, Eduardo (2018), Visión artificial, gráficos y neurocomputación, aplicaciones del álgebra geométrica, vol. I, Springer, ISBN 978-3-319-74830-6
- Breuils, Stéphane (2018). Estructura algorítmica para los operadores de Algèbres Géométriques y aplicaciones en superficies cuadriplicadas (PDF) (PHD). université-paris-est. Archivado (PDF) desde el original el 14 de julio de 2019.
- Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018), Una invitación del álgebra geométrica a la física del espacio-tiempo, la robótica y la geometría molecular, Springer, pp. 1–, ISBN 978-3-319-90665-2
- Hrdina, Jaroslav; Návrat, Aleš; Vašík, Petr (2018), "Álgebra geométrica para cónicas", Avances en álgebras aplicadas de Clifford , 28 (3), doi :10.1007/s00006-018-0879-2, S2CID 125649450
- Breuils, Stéphane; Fuchs, Laurent; Hitzer, Eckhard; Nozick, Vincent; Sugimoto, Akihiro (2019), "Cuádricas tridimensionales en álgebras geométricas conformes extendidas de dimensiones superiores a partir de puntos de control, ecuaciones implícitas y alineación de ejes" (PDF) , Advances in Applied Clifford Algebras , 29 (3), doi :10.1007/s00006-019-0974-z, S2CID 253597480
- Josipović, Miroslav (2019), Multiplicación geométrica de vectores: una introducción al álgebra geométrica en física, Springer International Publishing; Birkhäuser, pág. 256, ISBN 978-3-030-01756-9
- Hadfield, Hugo; Lasenby, Joan (2020), "Dinámica restringida en álgebra geométrica proyectiva y conforme", Advances in Computer Graphics , Lecture Notes in Computer Science, vol. 12221, págs. 459–471, doi :10.1007/978-3-030-61864-3_39, ISBN 978-3-030-61863-6, Identificador único 224820480
- Wu, Bofeng (2022), "Un marco de álgebra geométrica invariante de firma para la física del espacio-tiempo y sus aplicaciones en la dinámica relativista de una partícula masiva y la precesión giroscópica", Scientific Reports , 12 (1): 3981, arXiv : 2111.07353 , Bibcode :2022NatSR..12.3981W, doi :10.1038/s41598-022-06895-0, PMC 8901677 , PMID 35256628
- Wilmot, GP (2023), "El álgebra de la geometría", GitHub
- Lengyel, Eric (2024), Álgebra geométrica proyectiva iluminada , Lincoln, California: Terathon Software LLC, ISBN 979-8-9853582-5-4
Enlaces externos
- Un estudio del álgebra geométrica y el cálculo geométrico Alan Macdonald, Luther College, Iowa
- Los números imaginarios no son reales: el álgebra geométrica del espacio-tiempo. Introducción (Grupo de Cambridge GA)
- Álgebra geométrica 2015, Máster en informática científica, a cargo del Dr. Chris Doran (Cambridge)
- Matemáticas para programadores (de juegos): 5 métodos multivectoriales: introducción completa y referencia para programadores, de Ian Bell
- Escuela de verano IMPA 2010 Fernandes Oliveira Introducción y diapositivas
- Universidad de Fukui ESM Hitzer y publicaciones de GA de Japón
- Grupo de Google para GA
- Introducción al álgebra geométrica, Jaap Suter
- Recursos de álgebra geométrica Wiki seleccionada por Pablo Bleyer
- Álgebras geométricas aplicadas en informática e ingeniería Actas preliminares de 2018
- Sitio web de la comunidad de Álgebra geométrica para CGI, visión e ingeniería de bivector.net
- Vídeos de AGACSE 2021
Traducciones al inglés de libros y artículos antiguos
- G. Combebiac, "Cálculo de tricuaterniones" (Tesis doctoral)
- M. Markic, "Transformantes: un nuevo vehículo matemático. Una síntesis de los tricuaterniones de Combebiac y el sistema geométrico de Grassmann. El cálculo de los cuaterniones cuadri"
- C. Burali-Forti, "El método Grassmann en geometría proyectiva" Una recopilación de tres notas sobre la aplicación del álgebra exterior a la geometría proyectiva
- C. Burali-Forti, "Introducción a la geometría diferencial, siguiendo el método de H. Grassmann" Primer libro sobre la aplicación del álgebra de Grassmann
- H. Grassmann, "Mecánica, según los principios de la teoría de la extensión" – uno de sus artículos sobre las aplicaciones del álgebra exterior
Grupos de investigación
- Cálculo geométrico internacional. Enlaces a grupos de investigación, software y conferencias de todo el mundo
- Grupo de Álgebra Geométrica de Cambridge. Publicaciones en línea de texto completo y otros materiales
- Grupo de la Universidad de Ámsterdam
- Investigación y desarrollo del cálculo geométrico (archivo del sitio web de Hestenes en la Universidad Estatal de Arizona)
- Archivo de blogs y boletines informativos de GA-Net. Noticias sobre el desarrollo del Álgebra geométrica y el Álgebra de Clifford
- Álgebra Geométrica para Sistemas de Percepción-Acción. Grupo de Cibernética Geométrica (CINVESTAV, Campus Guadalajara, México)


















































![{\displaystyle a_{1}a_{2}a_{3}\puntos a_{n}=\sum _{i=0}^{[{\frac {n}{2}}]}\sum _{\mu \in {}{\mathcal {C}}}(-1)^{k}\operatorname {Pf} (a_{\mu _{1}}\cdot a_{\mu _{2}},\puntos ,a_{\mu _{2i-1}}\cdot a_{\mu _{2i}})a_{\mu _{2i+1}}\land \puntos \land a_{\mu _{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3fbfcface4d9d348b1b76c9718276f343c8f197)









![{\displaystyle [\mathbf {A} ]_{ij}=a_{i}\cdot a_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5207597ca24e5f3fc11785e33dd676e5565e164f)



![{\displaystyle \sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {A} ]_{kl}[\mathbf {O} ^{\mathrm {T} }]_{ lj}=\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {O} ]_{jl}[\mathbf {A} ]_{kl}=[\mathbf {D } ]_{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c169d06e467c5c7959e7da65c5b01b1bb89a4d05)

![{\displaystyle e_{i}=\sum _{j}[\mathbf {O} ]_{ij}a_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb80eb1d95f0720fd0d25abff339a0aed390074e)
![{\displaystyle e_{i}\cdot e_{j}=[\mathbf {D} ]_{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4620f4330bb5f5260c8978c2b7340df0c54f3725)

![{\displaystyle {\begin{array}{rl}e_{1}e_{2}\cdots e_{r}&=e_{1}\wedge e_{2}\wedge \cdots \wedge e_{r}\\&=\left(\sum _{j}[\mathbf {O} ]_{1j}a_{j}\right)\wedge \left(\sum _{j}[\mathbf {O} ]_{2j}a_{j}\right)\wedge \cdots \wedge \left(\sum _{j}[\mathbf {O} ]_{rj}a_{j}\right)\\&=(\det \mathbf {O} )a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426956a7cc82e46726be135237774216bddee9f2)






























![{\displaystyle {\operatorname {Pin} }\cap {\mathcal {G}}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8af5cdf87268cbad19d1ebf6fc3ad33aacc107f0)













![{\displaystyle A^{[0]}=\langle A\rangle _{0}+\langle A\rangle _{2}+\langle A\rangle _{4}+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c98172d77054c94548d89e3f67eb191414dfca)
![{\displaystyle A^{[1]}=\langle A\rangle _{1}+\langle A\rangle _{3}+\langle A\rangle _{5}+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/48de178eb8ca31db80f3cd707746e5eb677d3082)


![{\displaystyle {\mathcal {G}}^{[0]}(2,0)\cong {\mathcal {G}}(0,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ae6e508667a0ad2e905aefda0696bfa135bbfe)
![{\displaystyle {\mathcal {G}}^{[0]}(1,3)\cong {\mathcal {G}}(3,0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbe455ddcfa2303bf700b87f4c470fcf973c81ca)


































































































































































































































