Superficie sustentadora

Un perfil aerodinámico ( en inglés americano ) o aerofoil ( en inglés británico ) es un cuerpo aerodinámico que es capaz de generar significativamente más sustentación que resistencia . ^[1] Las alas, las velas y las palas de las hélices son ejemplos de perfiles aerodinámicos. Los perfiles de función similar diseñados con agua como fluido de trabajo se denominan hidroplanos .

Cuando se orienta en un ángulo adecuado, un cuerpo sólido que se mueve a través de un fluido desvía el fluido que se aproxima (para aeronaves de ala fija, una fuerza hacia abajo), lo que resulta en una fuerza sobre el perfil aerodinámico en la dirección opuesta a la desviación. ^{[2] [3]} Esta fuerza se conoce como fuerza aerodinámica y se puede descomponer en dos componentes: sustentación ( perpendicular a la velocidad de la corriente libre remota ) y resistencia ( paralela a la velocidad de la corriente libre).

La sustentación de un perfil aerodinámico es principalmente el resultado de su ángulo de ataque . La mayoría de las formas de perfil requieren un ángulo de ataque positivo para generar sustentación, pero los perfiles aerodinámicos combados pueden generar sustentación con un ángulo de ataque cero. Los perfiles aerodinámicos pueden diseñarse para su uso a diferentes velocidades modificando su geometría: los destinados al vuelo subsónico suelen tener un borde de ataque redondeado , mientras que los diseñados para el vuelo supersónico tienden a ser más delgados con un borde de ataque afilado. Todos tienen un borde de salida afilado . ^[4]

El aire desviado por un perfil aerodinámico hace que genere una "sombra" de menor presión por encima y por detrás de sí mismo. Esta diferencia de presión va acompañada de una diferencia de velocidad, a través del principio de Bernoulli , por lo que el campo de flujo resultante alrededor del perfil aerodinámico tiene una velocidad media más alta en la superficie superior que en la superficie inferior. ^[5] En algunas situaciones (por ejemplo, flujo potencial no viscoso ), la fuerza de sustentación se puede relacionar directamente con la diferencia de velocidad media superior/inferior sin calcular la presión utilizando el concepto de circulación y el teorema de Kutta-Joukowski . ^[6]

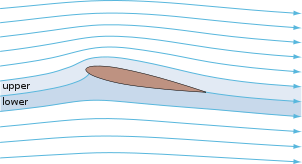
Las alas y los estabilizadores de los aviones de ala fija , así como las palas de rotor de los helicópteros , están construidos con secciones transversales en forma de perfil aerodinámico. Los perfiles aerodinámicos también se encuentran en hélices, ventiladores , compresores y turbinas . Las velas también son perfiles aerodinámicos, y las superficies submarinas de los veleros, como la orza , el timón y la quilla , son similares en sección transversal y funcionan con los mismos principios que los perfiles aerodinámicos. Las criaturas nadadoras y voladoras e incluso muchas plantas y organismos sésiles emplean perfiles aerodinámicos/hidroplanos: ejemplos comunes son las alas de las aves, los cuerpos de los peces y la forma de los dólares de arena . Un ala con forma de perfil aerodinámico puede crear carga aerodinámica en un automóvil u otro vehículo de motor, mejorando la tracción .

Cuando el viento se ve obstaculizado por un objeto, como una placa plana, un edificio o la cubierta de un puente, el objeto experimentará resistencia y también una fuerza aerodinámica perpendicular al viento. Esto no significa que el objeto califique como un perfil aerodinámico. Los perfiles aerodinámicos son formas de sustentación altamente eficientes, capaces de generar más sustentación que placas planas de tamaño similar de la misma área y capaces de generar sustentación con significativamente menos resistencia. Los perfiles aerodinámicos se utilizan en el diseño de aeronaves, hélices, palas de rotor, turbinas eólicas y otras aplicaciones de la ingeniería aeronáutica.

A la derecha se muestra una curva de sustentación y resistencia obtenida en pruebas en túnel de viento . La curva representa un perfil aerodinámico con una curvatura positiva , por lo que se produce cierta sustentación en un ángulo de ataque cero. Con un ángulo de ataque mayor, la sustentación aumenta en una relación aproximadamente lineal, llamada pendiente de la curva de sustentación. A unos 18 grados, este perfil aerodinámico entra en pérdida y la sustentación cae rápidamente más allá de ese punto. La caída de la sustentación se puede explicar por la acción de la capa límite de la superficie superior , que se separa y se engrosa en gran medida sobre la superficie superior en el ángulo de pérdida y más allá. El espesor de desplazamiento de la capa límite engrosada cambia la forma efectiva del perfil aerodinámico, en particular reduce su curvatura efectiva , lo que modifica el campo de flujo general para reducir la circulación y la sustentación. La capa límite más gruesa también provoca un gran aumento de la resistencia a la presión , de modo que la resistencia general aumenta bruscamente cerca y más allá del punto de pérdida.

El diseño de los perfiles aerodinámicos es una faceta importante de la aerodinámica . Los distintos perfiles aerodinámicos sirven para distintos regímenes de vuelo. Los perfiles aerodinámicos asimétricos pueden generar sustentación en un ángulo de ataque cero, mientras que un perfil aerodinámico simétrico puede ser más adecuado para vuelos invertidos frecuentes como en un avión acrobático . En la región de los alerones y cerca de la punta del ala, se puede utilizar un perfil aerodinámico simétrico para aumentar el rango de ángulos de ataque y evitar la pérdida de sustentación . De este modo, se puede utilizar un amplio rango de ángulos sin separación de la capa límite . Los perfiles aerodinámicos subsónicos tienen un borde de ataque redondeado, que naturalmente es insensible al ángulo de ataque. Sin embargo, la sección transversal no es estrictamente circular: el radio de curvatura se aumenta antes de que el ala alcance el grosor máximo para minimizar la posibilidad de separación de la capa límite. Esto alarga el ala y mueve el punto de grosor máximo hacia atrás desde el borde de ataque.

Los perfiles aerodinámicos supersónicos tienen una forma mucho más angular y pueden tener un borde de ataque muy agudo, que es muy sensible al ángulo de ataque. Un perfil aerodinámico supercrítico tiene su espesor máximo cerca del borde de ataque para tener una gran longitud para hacer que el flujo supersónico vuelva lentamente a velocidades subsónicas. Generalmente, estos perfiles aerodinámicos transónicos y también los supersónicos tienen una comba baja para reducir la divergencia de la resistencia . Las alas de los aviones modernos pueden tener diferentes secciones de perfil aerodinámico a lo largo de la envergadura, cada una optimizada para las condiciones en cada sección del ala.

Los flaps y, a veces, los slats , son dispositivos móviles de alta sustentación que se instalan en los perfiles aerodinámicos de casi todos los aviones. Un flap de borde de salida actúa de manera similar a un alerón; sin embargo, a diferencia de este último, puede retraerse parcialmente dentro del ala si no se utiliza.

Un ala de flujo laminar tiene un espesor máximo en la línea de comba media. Analizando las ecuaciones de Navier-Stokes en el régimen lineal se muestra que un gradiente de presión negativo a lo largo del flujo tiene el mismo efecto que reducir la velocidad. Así que con la comba máxima en el medio, es posible mantener un flujo laminar sobre un porcentaje mayor del ala a una velocidad de crucero más alta. Sin embargo, cierta contaminación de la superficie interrumpirá el flujo laminar, haciéndolo turbulento. Por ejemplo, con lluvia en el ala, el flujo será turbulento. Bajo ciertas condiciones, los restos de insectos en el ala también causarán la pérdida de pequeñas regiones de flujo laminar. ^[7] Antes de la investigación de la NASA en los años 1970 y 1980, la comunidad de diseño de aeronaves entendió a partir de los intentos de aplicación en la era de la Segunda Guerra Mundial que los diseños de alas de flujo laminar no eran prácticos usando tolerancias de fabricación comunes e imperfecciones de la superficie. Esa creencia cambió después de que se desarrollaran nuevos métodos de fabricación con materiales compuestos (por ejemplo, los perfiles aerodinámicos de flujo laminar desarrollados por el profesor Franz Wortmann para su uso con alas hechas de plástico reforzado con fibra ). También se introdujeron métodos de mecanizado de metal. La investigación de la NASA en la década de 1980 reveló la practicidad y utilidad de los diseños de alas de flujo laminar y abrió el camino para aplicaciones de flujo laminar en superficies de aeronaves prácticas modernas, desde aeronaves de aviación general subsónicas hasta aeronaves de transporte grandes transónicas, pasando por diseños supersónicos. ^[8]

Se han ideado esquemas para definir perfiles aerodinámicos; un ejemplo es el sistema NACA . También se utilizan varios sistemas de generación de perfiles aerodinámicos. Un ejemplo de perfil aerodinámico de uso general que encuentra una amplia aplicación y es anterior al sistema NACA es el Clark-Y . Hoy en día, los perfiles aerodinámicos se pueden diseñar para funciones específicas mediante el uso de programas informáticos.

A continuación se definen los distintos términos relacionados con los perfiles aerodinámicos: ^[9]

• La superficie de succión (también conocida como superficie superior) generalmente se asocia con una mayor velocidad y una menor presión estática.
• La superficie de presión (también conocida como superficie inferior) tiene una presión estática comparativamente más alta que la superficie de succión. El gradiente de presión entre estas dos superficies contribuye a la fuerza de sustentación generada para un perfil aerodinámico determinado.

La geometría del perfil aerodinámico se describe con una variedad de términos:

• El borde de ataque es el punto en la parte delantera del perfil aerodinámico que tiene la máxima curvatura (radio mínimo). ^[10]
• El borde de salida es el punto del perfil aerodinámico más alejado del borde de ataque. El ángulo entre las superficies superior e inferior en el borde de salida es el ángulo del borde de salida .
• La línea de cuerda es la línea recta que une los bordes de ataque y de salida. La longitud de la cuerda , o simplemente cuerda , es la longitud de la línea de cuerda. Esa es la dimensión de referencia de la sección del perfil aerodinámico.${\estilo de visualización c}$

La forma del perfil aerodinámico se define utilizando los siguientes parámetros geométricos:

• La línea de comba media o línea media es el lugar geométrico de los puntos intermedios entre las superficies superior e inferior. Su forma depende de la distribución del espesor a lo largo de la cuerda;
• El espesor de un perfil aerodinámico varía a lo largo de la cuerda. Puede medirse de dos maneras:
  • Espesor medido perpendicularmente a la línea de comba. ^{[11] [12]} Esto a veces se describe como la "convención americana"; ^[11]
  • Espesor medido perpendicularmente a la línea de la cuerda. ^[13] Esto a veces se describe como la "convención británica".

Algunos parámetros importantes para describir la forma de un perfil aerodinámico son su comba y su espesor . Por ejemplo, un perfil aerodinámico de la serie NACA de 4 dígitos como el NACA 2415 (que debe leerse como 2 – 4 – 15) describe un perfil aerodinámico con una comba de 0,02 cuerdas ubicada en 0,40 cuerdas, con 0,15 cuerdas de espesor máximo.

Finalmente, los conceptos importantes utilizados para describir el comportamiento del perfil aerodinámico al moverse a través de un fluido son:

• El centro aerodinámico , que es la ubicación a lo largo de la cuerda alrededor de la cual el momento de cabeceo es independiente del coeficiente de sustentación y del ángulo de ataque.
• El centro de presión , que es la ubicación a lo largo de la cuerda en la que el momento de cabeceo es momentáneamente cero. En un perfil aerodinámico combado, el centro de presión no es una ubicación fija, ya que se mueve en respuesta a los cambios en el ángulo de ataque y el coeficiente de sustentación.

En un flujo bidimensional alrededor de un ala uniforme de envergadura infinita, la pendiente de la curva de sustentación está determinada principalmente por el ángulo del borde de salida . La pendiente es máxima si el ángulo es cero y disminuye a medida que el ángulo aumenta. ^{[14] [15]} Para un ala de envergadura finita, la relación de aspecto del ala también influye significativamente en la pendiente de la curva. A medida que disminuye la relación de aspecto, la pendiente también disminuye. ^[16]

La teoría de los perfiles aerodinámicos delgados es una teoría simple de los perfiles aerodinámicos que relaciona el ángulo de ataque con la sustentación para flujos incompresibles y no viscosos . Fue ideada por el matemático alemán Max Munk y refinada por el aerodinámico británico Hermann Glauert y otros ^[17] en la década de 1920. La teoría idealiza el flujo alrededor de un perfil aerodinámico como un flujo bidimensional alrededor de un perfil aerodinámico delgado. Se puede imaginar como abordando un perfil aerodinámico de espesor cero y envergadura infinita .

La teoría de los perfiles aerodinámicos delgados fue particularmente notable en su época porque proporcionó una base teórica sólida para las siguientes propiedades importantes de los perfiles aerodinámicos en flujo no viscoso bidimensional: ^{[18] [19]}

1. En un perfil aerodinámico simétrico, el centro de presión y el centro aerodinámico coinciden y se encuentran exactamente a un cuarto de la cuerda detrás del borde de ataque.
2. En un perfil aerodinámico curvado , el centro aerodinámico se encuentra exactamente a un cuarto de la cuerda detrás del borde de ataque, pero la posición del centro de presión se mueve cuando cambia el ángulo de ataque.
3. La pendiente del coeficiente de sustentación en función de la línea del ángulo de ataque se expresa en unidades por radián.${\estilo de visualización 2\pi \!}$

Como consecuencia de (3), el coeficiente de sustentación de la sección de un perfil aerodinámico delgado y simétrico de envergadura infinita es:

${\displaystyle \ c_{l}=2\pi \alpha }$

¿Dónde está el coeficiente de sustentación de la sección?${\displaystyle c_{l}\!}$

${\estilo de visualización \alfa \!}$es el ángulo de ataque en radianes, medido en relación con la línea de cuerda .

(La expresión anterior también es aplicable a un perfil aerodinámico curvado, donde el ángulo de ataque se mide en relación con la línea de sustentación cero en lugar de la línea de cuerda).${\estilo de visualización \alfa \!}$

También como consecuencia de (3), el coeficiente de sustentación de la sección de un perfil aerodinámico curvado de envergadura infinita es:

${\displaystyle \ c_{l}=c_{l_{0}}+2\pi \alpha }$

donde es el coeficiente de sustentación de la sección cuando el ángulo de ataque es cero.${\displaystyle \ c_{l_{0}}}$

La teoría de los perfiles aerodinámicos delgados supone que el aire es un fluido no viscoso , por lo que no tiene en cuenta el estancamiento del perfil aerodinámico, que suele producirse en un ángulo de ataque de entre 10° y 15° para los perfiles aerodinámicos típicos. ^[20] Sin embargo, a mediados y finales de la década de 2000, Wallace J. Morris II propuso en su tesis doctoral una teoría que predecía el inicio del estancamiento en el borde de ataque. ^[21] Los refinamientos posteriores de Morris contienen los detalles sobre el estado actual del conocimiento teórico sobre el fenómeno del estancamiento en el borde de ataque. ^{[22] [23]} La teoría de Morris predice el ángulo de ataque crítico para el inicio del estancamiento en el borde de ataque como la condición en la que se predice una zona de separación global en la solución para el flujo interno. ^[24] La teoría de Morris demuestra que un flujo subsónico alrededor de un perfil aerodinámico delgado se puede describir en términos de una región exterior, alrededor de la mayor parte de la cuerda del perfil aerodinámico, y una región interior, alrededor de la nariz, que coinciden asintóticamente entre sí. Como el flujo en la región exterior está dominado por la teoría clásica de perfiles aerodinámicos delgados, las ecuaciones de Morris exhiben muchos componentes de la teoría de perfiles aerodinámicos delgados.

En la teoría de perfiles aerodinámicos delgados, se supone que el ancho del perfil aerodinámico (2D) es insignificante y que el perfil aerodinámico en sí se reemplaza por una pala 1D a lo largo de su línea de curvatura, orientada en el ángulo de ataque α . Sea x la posición a lo largo de la pala , que va desde 0 en la parte delantera del ala hasta c en el borde de salida; se supone que la curvatura del perfil aerodinámico, dy ⁄ dx , es suficientemente pequeña como para que no sea necesario distinguir entre x y la posición relativa al fuselaje. ^{[25] [26]}

El flujo a través del perfil aerodinámico genera una circulación alrededor de la pala, que se puede modelar como una lámina de vórtice de fuerza variable según la posición γ( x ) . La condición de Kutta implica que γ( c )=0 , pero la fuerza es singular en el frente de la pala, con γ( x )∝ 1 ⁄ √ x para x ≈ 0 . ^[27] Si el flujo principal V tiene densidad ρ , entonces el teorema de Kutta-Joukowski da que la fuerza de sustentación total F es proporcional a ^{[28] [29]} y su momento M sobre el borde de ataque proporcional a ^[27]$${\displaystyle \rho V\int _{0}^{c}\gamma (x)\,dx}$$ $${\displaystyle \rho V\int _{0}^{c}x\;\gamma (x)\,dx.}$$

De acuerdo con la ley de Biot-Savart , la vorticidad γ( x ) produce un campo de flujo orientado de manera normal al perfil aerodinámico en x . Dado que el perfil aerodinámico es una superficie impermeable , el flujo debe equilibrar un flujo inverso desde V . Por la aproximación de ángulo pequeño , V está inclinado en un ángulo α- dy ⁄ dx con respecto al álabe en la posición x , y el componente normal es correspondientemente (α- dy ⁄ dx ) V . Por lo tanto, γ( x ) debe satisfacer la ecuación de convolución que lo determina de manera única en términos de cantidades conocidas. ^{[28] [30]}$${\displaystyle w(x)={\frac {1}{2\pi }}\int _{0}^{c}{\frac {\gamma (x')}{xx'}}\,dx'{\text{,}}}$$${\estilo de visualización w(x)}$ $${\displaystyle \left(\alpha -{\frac {dy}{dx}}\right)V=-w(x)=-{\frac {1}{2\pi }}\int _{0}^{c}{\frac {\gamma (x')}{xx'}}\,dx'{\text{,}}}$$

Se puede obtener una solución explícita cambiando primero las variables y luego expandiendo tanto dy ⁄ dx como γ( x ) como una serie de Fourier no dimensionalizada en θ con un término principal modificado: la sustentación y el momento resultantes dependen solo de los primeros términos de esta serie. ^[31]$${\displaystyle x=c\cdot {\frac {1+\cos(\theta )}{2}},}$$$${\displaystyle {\begin{aligned}&{\frac {dy}{dx}}=A_{0}+A_{1}\cos(\theta )+A_{2}\cos(2\theta )+\dots \\&\gamma (x)=2(\alpha +A_{0})\left({\frac {\sin \theta }{1+\cos \theta }}\right)+2A_{1}\sin(\theta )+2A_{2}\sin(2\theta )+\dots {\text{.}}\end{aligned}}}$$

El coeficiente de sustentación satisface y el coeficiente de momento ^[32] El momento alrededor del punto de 1/4 de cuerda será entonces De esto se deduce que el centro de presión está detrás del punto de 'cuarto de cuerda' 0,25 c , por El centro aerodinámico es la posición en la que el momento de cabeceo M ′ no varía con un cambio en el coeficiente de sustentación: ^[28] La teoría de perfiles aerodinámicos delgados muestra que, en un flujo no viscoso bidimensional, el centro aerodinámico está en la posición de un cuarto de cuerda.$${\displaystyle C_{L}=2\pi \left(\alpha +A_{0}+{\frac {A_{1}}{2}}\right)=2\pi \alpha +2\int _{0}^{\pi }{{\frac {dy}{dx}}\cdot (1+\cos \theta )\,d\theta }}$$ $${\displaystyle C_{M}=-{\frac {\pi }{2}}\left(\alpha +A_{0}+A_{1}-{\frac {A_{2}}{2}}\right)=-{\frac {\pi }{2}}\alpha -\int _{0}^{\pi }{{\frac {dy}{dx}}\cdot \cos(\theta )(1+\cos \theta )\,d\theta }{\text{.}}}$$$${\displaystyle C_{M}(1/4c)=-\pi /4(A_{1}-A_{2}){\text{.}}}$$$${\displaystyle \Delta x/c=\pi /4((A_{1}-A_{2})/C_{L}){\text{.}}}$$ $${\displaystyle {\frac {\partial (C_{M'})}{\partial (C_{L})}}=0{\text{.}}}$$

• Ala de control de circulación
• Hidroala
• Perfil aerodinámico Kline-Fogleman
• Efecto Küssner
• Parapente
• Configuración del ala

• Anderson, John, D (2007). Fundamentos de aerodinámica . McGraw-Hill.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Ali Kamranpay, Alireza Mehrabadi. Análisis numérico del perfil aerodinámico NACA 0012 en diferentes ángulos de ataque y obtención de sus coeficientes aerodinámicos. Journal of Mechatronics and Automation. 2019; 6(3): 8–16p.
• Bearman, Matt (2019). “¿Seguir la corriente? La contribución de Gran Bretaña a la investigación sobre flujo laminar, 1930-1947”. The Aviation Historian (29): 74-87. ISSN  2051-1930.

Wikimedia Commons alberga una categoría multimedia sobre Perfiles aerodinámicos y secciones transversales de alas .

• Base de datos de coordenadas de perfil aerodinámico de la UIUC
• Aplicación de referencia para perfiles aerodinámicos e hidroplanos
• FoilSim Un simulador de perfil aerodinámico de la NASA
• Airfoil Playground: aplicación web interactiva
• Escritorio aero
• Flujo de aire a través de un ala (Universidad de Cambridge)