Flujo de calor

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Flujo de calor» – noticias  · periódicos  · libros  · académico  · JSTOR ( marzo de 2021 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Flujo de calor
Flujo de calor a través de una superficie.${\displaystyle {\vec {\phi }}_{\mathrm {q} }}$
Símbolos comunes	${\displaystyle {\vec {\phi }}_{\mathrm {q} }}$
Unidad SI	W/ m2
Otras unidades	Btu/(h⋅pies cuadrados )
En unidades base del SI	kg⋅s −3
Dimensión	${\displaystyle {\mathsf {M}}{\mathsf {T}}^{-3}}$

En física e ingeniería , el flujo de calor o flujo térmico , a veces también denominado densidad de flujo de calor ^[1] , densidad de flujo de calor o intensidad de la tasa de flujo de calor , es un flujo de energía por unidad de área por unidad de tiempo . Sus unidades del SI son vatios por metro cuadrado (W/m2 ⁾ . Tiene una dirección y una magnitud, por lo que es una cantidad vectorial . Para definir el flujo de calor en un punto determinado del espacio, se toma el caso límite en el que el tamaño de la superficie se vuelve infinitesimalmente pequeño.

El flujo de calor se suele denotar con el subíndice q, que especifica el flujo de calor , en contraposición al flujo de masa o de momento . La ley de Fourier es una aplicación importante de estos conceptos.${\displaystyle {\vec {\phi }}_{\mathrm {q} }}$

Para la mayoría de los sólidos en condiciones normales, el calor se transporta principalmente por conducción y el flujo de calor se describe adecuadamente mediante la ley de Fourier.

$${\displaystyle \phi _{\text{q}}=-k{\frac {\mathrm {d} T(x)}{\mathrm {d} x}}}$$

donde es la conductividad térmica . El signo negativo muestra que el flujo de calor se mueve desde regiones de mayor temperatura a regiones de menor temperatura.${\estilo de visualización k}$

El caso multidimensional es similar, el flujo de calor va "hacia abajo" y, por lo tanto, el gradiente de temperatura tiene signo negativo:

$${\displaystyle {\vec {\phi }}_{\mathrm {q} }=-k\nabla T}$$¿Dónde está el operador de gradiente ?${\displaystyle {\nabla}}$

La medición del flujo de calor se puede realizar de diferentes maneras.

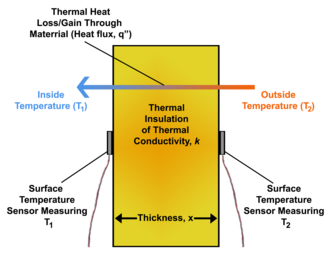
Un método conocido, pero a menudo poco práctico, consiste en medir la diferencia de temperatura en una pieza de material con una conductividad térmica conocida . Este método es análogo a una forma estándar de medir una corriente eléctrica, en la que se mide la caída de tensión en una resistencia conocida . Por lo general, este método es difícil de realizar, ya que a menudo no se conoce la resistencia térmica del material que se está probando. Se necesitarían valores precisos del espesor y la conductividad térmica del material para determinar la resistencia térmica. Utilizando la resistencia térmica, junto con las mediciones de temperatura en ambos lados del material, se puede calcular indirectamente el flujo de calor.

Un segundo método para medir el flujo de calor es mediante el uso de un sensor de flujo de calor , o transductor de flujo de calor, para medir directamente la cantidad de calor que se transfiere hacia/desde la superficie en la que está montado el sensor de flujo de calor. El tipo más común de sensor de flujo de calor es una termopila de temperatura diferencial que funciona esencialmente con el mismo principio que el primer método de medición que se mencionó, excepto que tiene la ventaja de que la resistencia/conductividad térmica no necesita ser un parámetro conocido. Estos parámetros no tienen que ser conocidos ya que el sensor de flujo de calor permite una medición in situ del flujo de calor existente utilizando el efecto Seebeck . Sin embargo, los sensores de flujo de calor de termopila diferencial tienen que calibrarse para relacionar sus señales de salida [μV] con los valores de flujo de calor [W/(m ² ⋅K)]. Una vez que el sensor de flujo de calor está calibrado, puede usarse para medir directamente el flujo de calor sin requerir el valor raramente conocido de la resistencia térmica o la conductividad térmica.

Una de las herramientas que tiene a su disposición un científico o un ingeniero es el balance energético . Este balance se puede establecer para cualquier sistema físico, desde reactores químicos hasta organismos vivos, y generalmente adopta la siguiente forma:

${\displaystyle {\big .}{\frac {\partial E_{\mathrm {entrada}}}{\partial t}}-{\frac {\partial E_{\mathrm {salida}}}{\partial t}}-{\frac {\partial E_{\mathrm {acumulada}}}{\partial t}}=0}$

donde los tres términos representan la tasa de cambio temporal de la cantidad total de energía entrante, la cantidad total de energía saliente y la cantidad total de energía acumulada, respectivamente.${\displaystyle {\big .}{\frac {\parcial E}{\parcial t}}}$

Ahora bien, si la única forma en que el sistema intercambia energía con su entorno es a través de la transferencia de calor, la tasa de calor se puede utilizar para calcular el balance energético, ya que

${\displaystyle {\frac {\partial E_{\mathrm {entrada}}}{\partial t}}-{\frac {\partial E_{\mathrm {salida}}}{\partial t}}=\oint _{S}{\vec {\phi }}_{\mathrm {q} }\cdot \,\mathrm {d} {\vec {S}}}$

donde hemos integrado el flujo de calor sobre la superficie del sistema.${\displaystyle {\vec {\phi }}_{\mathrm {q} }}$${\estilo de visualización S}$

En aplicaciones del mundo real no se puede conocer el flujo de calor exacto en cada punto de la superficie, pero se pueden utilizar esquemas de aproximación para calcular la integral, por ejemplo, la integración de Monte Carlo .

• Flujo radiante
• Flujo de calor latente
• Tasa de flujo de calor
• Insolación
• Sensor de flujo de calor
• Conducción de calor relativista