Cuadrícula de círculos superpuestos
Este artículo tiene problemas que pueden hacer que algunos textos o imágenes sean ilegibles o difíciles de leer en el modo oscuro. Los lectores de escritorio pueden cambiar al modo claro temporalmente usando el ícono de anteojos en la parte superior de la página. ( Septiembre de 2024 ) |
| Cuadrícula de círculo cuadrado | |||||
|---|---|---|---|---|---|
| 1+ |  |  |  |  |  |
| 4 |  |  |  |  |  |
| 9 |  |  |  |  |  |
| Formas de celosía cuadrada centrada | |||||
| 5 |  |  |  |  |  |
| 13 |  |  |  |  |  |
 |  |  |  |  | |
| cuadrícula circular triangular | |||||
| 1+ |  |  |  |  |  |
| 3 |  |  |  |  |  |
| 4 |  |  |  |  |  |
| 7 |  |  |  |  |  |
| 19 |  |  |  |  |  |
 |  |  |  |  | |
Una cuadrícula de círculos superpuestos es un patrón geométrico de círculos repetidos y superpuestos de igual radio en un espacio bidimensional . Comúnmente, los diseños se basan en círculos centrados en triángulos (con la forma simple de dos círculos llamada vesica piscis ) o en el patrón de celosía cuadrada de puntos.
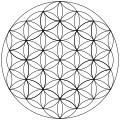
Los patrones de siete círculos superpuestos aparecen en artefactos históricos desde el siglo VII a. C. en adelante; se convirtieron en un adorno de uso frecuente en el período del Imperio Romano y sobrevivieron en las tradiciones artísticas medievales tanto en el arte islámico ( decoraciones girih ) como en el arte gótico . El patrón de círculos superpuestos recibe el nombre de "Flor de la Vida" en las publicaciones de la Nueva Era .
De especial interés es la roseta de seis pétalos derivada del patrón de "siete círculos superpuestos", también conocido como " Sol de los Alpes " por su uso frecuente en el arte popular alpino en los siglos XVII y XVIII.
Cuadrícula triangular de círculos superpuestos

La forma reticular triangular , con radios de círculos iguales a su separación, se denomina cuadrícula de siete círculos superpuestos . [1] Contiene 6 círculos que se intersecan en un punto, con un séptimo círculo centrado en esa intersección.
Los círculos superpuestos con construcciones geométricas similares se han utilizado con poca frecuencia en diversas artes decorativas desde la antigüedad. El patrón ha encontrado una amplia gama de usos en la cultura popular, la moda , la joyería , los tatuajes y los productos decorativos.
Importancia cultural
Próximo Oriente
El caso más antiguo conocido del patrón de "círculos superpuestos" data del siglo VII o VI a. C. y se encontró en el umbral del palacio del rey asirio Aššur-bāni-apli en Dur Šarrukin (ahora en el Louvre ). [2]
El diseño se vuelve más común en los primeros siglos de la era común. Un ejemplo temprano son cinco patrones de 19 círculos superpuestos dibujados en las columnas de granito del Templo de Osiris en Abydos , Egipto , [3] y otros cinco en la columna opuesta al edificio. Están dibujados en ocre rojo y algunos son muy tenues y difíciles de distinguir. [4] Los patrones son grafitis y no se encuentran en adornos nativos egipcios. En su mayoría datan de los primeros siglos de la era cristiana [5], aunque no se puede descartar con certeza su origen medieval o incluso moderno (principios del siglo XX), ya que los dibujos no se mencionan en las extensas listas de grafitis en el templo compiladas por Margaret Murray en 1904. [6]
En Inglaterra se utilizaban a veces patrones similares como marcas apotropaicas para impedir que las brujas entraran en los edificios. [7] Las cruces de consagración que indican puntos en las iglesias ungidos con agua bendita durante la dedicación de una iglesia también toman la forma de círculos superpuestos.
En el arte islámico , el patrón es una de las diversas combinaciones de círculos (otros se utilizan para diseños cuádruples o quíntuples) que se utilizan para construir cuadrículas para patrones geométricos islámicos . Se utiliza para diseñar patrones con estrellas de 6 y 12 puntas, así como hexágonos en el estilo llamado girih . Sin embargo, los patrones resultantes ocultan característicamente la cuadrícula de construcción, presentando en su lugar un diseño de correas entrelazadas . [8]
Europa
Se encuentran patrones de siete círculos superpuestos en mosaicos romanos, por ejemplo en el palacio de Herodes en el siglo I a. C. [9]
El diseño se encuentra en una de las placas de plata del tesoro romano tardío de Kaiseraugst (descubierto en 1961). [10] Más tarde se encuentra como adorno en la arquitectura gótica y aún más tarde en el arte popular europeo del período moderno temprano.
Entre los ejemplos de la Alta Edad Media se encuentran los pavimentos Cosmati de la Abadía de Westminster (siglo XIII). [11] Leonardo da Vinci analizó explícitamente las proporciones matemáticas del diseño. [12]
Uso moderno
.jpg/440px-Flower_of_Life_pendant_(2).jpg)
Colgante de 19 círculos con arcos , plata, ⌀ 27 mm
(producto comercial, 2013)
El nombre “Flor de la Vida” es moderno, se asocia con el movimiento de la Nueva Era y se le atribuye comúnmente a Drunvalo Melchizedek en su libro El antiguo secreto de la Flor de la Vida (1999). [13] [14]
El patrón y el nombre moderno se han propagado en una amplia gama de usos en la cultura popular, en la moda, la joyería, los tatuajes y los productos decorativos. El patrón en acolchado se ha llamado anillo de bodas de diamantes o anillo de bodas de triángulo para contrastarlo con el patrón cuadrado. Además de un uso ocasional en la moda, [15] también se utiliza en las artes decorativas. Por ejemplo, el álbum Sempiternal (2013) de Bring Me the Horizon utiliza la cuadrícula de 61 círculos superpuestos como la característica principal de su portada, [16] mientras que el álbum A Head Full of Dreams (2015) de Coldplay presenta la cuadrícula de 19 círculos superpuestos como la parte central de su portada. Los carteles teaser que ilustran la portada de A Head Full of Dreams se exhibieron ampliamente en el metro de Londres en la última semana de octubre de 2015. [17]
El símbolo del "Sol de los Alpes" ( en italiano Sole delle Alpi ) se ha utilizado como emblema del nacionalismo padano en el norte de Italia desde la década de 1990. [18] Se asemeja a un patrón que se encuentra a menudo en esa zona en los edificios. [19]
Una "Flor de la Vida" de siete círculos también se utiliza en el escudo de armas de Asgardia, la nación espacial.
Galería
- Variante hexagonal de 1, 7 y 19 círculos
En los ejemplos siguientes, el patrón tiene un contorno hexagonal y está aún más circunscrito.
- Dibujo de Leonardo da Vinci del Códice Atlántico , entre 1478 y 1519.
- Dibujo de Leonardo da Vinci ( Códice Atlántico , fol. 307v)
- 1 círculo con arcos completados
- 7 círculos: suelo de mosaico de una casa de baños del palacio de Herodes , siglo I a. C.
- Símbolo de 19 círculos con arcos completados y delimitado por un círculo más grande
- 19 círculos: Dos símbolos dibujados en ocre rojo Templo de Osiris en Abydos, Egipto
- 19 círculos: Una ventana en el ábside sur de la iglesia del Monasterio de Preveli (Moni Preveli), Creta.
- Patrones similares
En los ejemplos siguientes el patrón no tiene un contorno hexagonal.
- Copa con escenas mitológicas, friso con esfinge y representación de un rey venciendo a sus enemigos. Ciproarcaico I (siglos VIII-VII a. C.). Procedente de Idalion, Chipre .
- Bola sostenida por el León Guardián Imperial macho en la Puerta de la Armonía Suprema , Ciudad Prohibida , Pekín , China, mostrando el patrón geométrico en su superficie.
- Decoración del suelo del palacio del rey Asurbanipal , en el norte de Irak , visible en el Museo del Louvre, fechada en el 645 a. C.
- Taza de café (Alemania, 2022)
- Emblema del " Sol de los Alpes " utilizado por la Liga Norte
Construcción
Martha Bartfeld, autora de libros tutoriales de arte geométrico, describió su descubrimiento independiente del diseño en 1968. Su definición original decía: "Este diseño consiste en círculos que tienen un radio de 1 pulgada; 25 mm, y cada punto de intersección sirve como un nuevo centro. El diseño se puede expandir hasta el infinito dependiendo de la cantidad de veces que se marquen los puntos impares".
La figura del patrón se puede dibujar con lápiz y compás , creando varias series de círculos entrelazados del mismo diámetro que toquen el centro del círculo anterior. El segundo círculo se centra en cualquier punto del primer círculo. Todos los círculos siguientes se centran en la intersección de otros dos círculos.
Progresiones
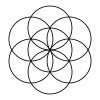
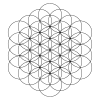
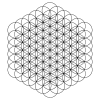
El patrón se puede extender hacia afuera en anillos hexagonales concéntricos de círculos, como se muestra. La primera fila muestra anillos de círculos. La segunda fila muestra una interpretación tridimensional de un conjunto de cubos de esferas de n × n × n vistos desde un eje diagonal. La tercera fila muestra el patrón completado con arcos de círculos parciales dentro de un conjunto de círculos completados.
Los conjuntos en expansión tienen 1, 7, 19, 37, 61, 91, 127, etc. círculos y anillos hexagonales de círculos cada vez más grandes. El número de círculos es n 3 -( n -1) 3 = 3 n 2 -3 n +1 = 3 n ( n -1)+1.
Estos círculos superpuestos también pueden verse como una proyección de un cubo de n unidades de esferas en un espacio tridimensional, visto desde el eje diagonal. Hay más esferas que círculos porque algunas se superponen en dos dimensiones.
| 1 círculo | 7 círculos (8-1) | 19 círculos (27-8) | 37 círculos (64-27) | 61 círculos (125-64) | 91 círculos (216-125) | 127 círculos... (343-216) |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| 1-esfera (1×1×1) | 8 esferas (2×2×2) | 27 esferas (3×3×3) | 64 esferas (4×4×4) | 125 esferas (5×5×5) | 216 esferas (6×6×6) | 343-esfera (7×7×7) |
 |  |  | (falta imagen) | (falta imagen) | (falta imagen) | (falta imagen) |
| +12 arcos | +24 arcos | +36 arcos | +48 arcos | +60 arcos | +72 arcos | +84 arcos |
 |  | 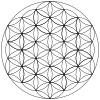 |  |  |  |  |
Otras variaciones
Otra forma de red triangular es común, con una separación de círculos igual a la raíz cuadrada de tres veces su radio. Richard Kershner demostró en 1939 que ninguna disposición de círculos puede cubrir el plano de manera más eficiente que esta disposición de red hexagonal. [20]
Dos copias offset de este patrón circular forman un patrón de mosaico rómbico , mientras que tres copias forman el patrón triangular original.
- Ejemplo de 19 círculos
- Dos copias offset del patrón circular mínimo que cubre el círculo (izquierda) forman un patrón de mosaico rómbico , como esta versión roja y azul.
- Tres copias offset del patrón circular mínimo que cubre el círculo (imagen más a la izquierda) forman el patrón de 7 círculos, como esta versión roja, verde y azul.
- Pavimento de mosaico blanco y negro en la Villa Adriana , Tívoli, siglo II d. C.
Conceptos relacionados
La lente central de la figura de dos círculos se llama vesica piscis , de Euclides . Dos círculos también se denominan círculos de Villarceau como intersección plana de un toro. Las áreas dentro de un círculo y fuera del otro círculo se denominan lune .
La figura de 3 círculos se asemeja a una representación de los anillos borromeos y se utiliza en los diagramas de Venn de la teoría de 3 conjuntos . Su interior forma un camino unicursal llamado triqueta . El centro de la figura de 3 círculos se llama triángulo de Reuleaux .
 Vesica piscis |  Anillos borromeos |  Diagrama de Venn |  Triqueta | 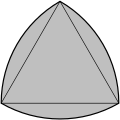 Triángulo de Reuleaux |
Algunos poliedros esféricos con aristas a lo largo de círculos máximos pueden proyectarse estereográficamente sobre el plano como círculos superpuestos.
 Octaedro |  Cuboctaedro | 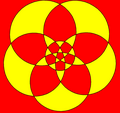 Icosidodecaedro |
El patrón de siete círculos también se ha llamado patrón islámico de siete círculos por su uso en el arte islámico .
Cuadrícula de círculos superpuestos
| ||
|
La forma de celosía cuadrada se puede ver con círculos que se alinean horizontal y verticalmente, mientras se cruzan en sus diagonales. El patrón parece ligeramente diferente cuando se gira en su diagonal, también se llama forma de celosía cuadrada centrada porque se puede ver como dos celosías cuadradas, cada una centrada en los espacios de la otra.
Se llama motivo Kawung en batik indonesio y se encuentra en las paredes del templo hindú del siglo VIII Prambanan en Java .
Se le llama Apsamikkum por las matemáticas de la antigua Mesopotamia . [21]
- La cuadrícula se puede ver en una red cúbica centrada en las caras , con 12 esferas en contacto alrededor de cada esfera.
- La cuadrícula de cinco círculos superpuestos relacionada se construye a partir de dos conjuntos de círculos superpuestos con un desplazamiento a la mitad. [22]
Véase también
- Teoría de nudos
- Mutaciones de simetría de teselación uniforme : mutaciones de patrones en el espacio 3D
Referencias
- ^ Arte islámico y diseño geométrico: actividades para aprender
- ^ Louvre Inv.-Nr. AO 19915. Georges Perrot, Charles Chipiez, Una historia del arte en Caldea y Asiria , vol. 1, Londres 1884, pág. 240, (gutenberg.org)
- ^ Weisstein, Eric W. "Flor de la vida". MathWorld .
- ^ Stewart, Malcolm (2008). «La «flor de la vida» y el Osirión: los hechos son más interesantes que la fantasía». Egyptian Tour (David Furlong) . Consultado el 8 de noviembre de 2015 .
- ^ Furlong, David. "El Osirión y la Flor de la Vida" . Consultado el 8 de noviembre de 2015 .Furlong afirma que estos grabados no pueden datar antes del 535 a. C. y probablemente datan del siglo II y IV d. C. Su investigación se basa en evidencia fotográfica de texto griego, aún por descifrar por completo. El texto se ve junto a los diseños y la posición cerca de la parte superior de las columnas, que tienen más de 4 metros de altura. Furlong sugiere que el Osirion estaba medio lleno de arena antes de que se dibujaran los círculos y, por lo tanto, es probable que haya sido mucho después del final de la dinastía ptolemaica .
- ^ Murray, Margaret Alice (1904). El Osireion en Abydos, Londres. pág. 35. Consultado el 4 de noviembre de 2015 .
- ^ Kennedy, Maev (31 de octubre de 2016). «Marcas de brujas: se pide al público que busque marcas antiguas en edificios». The Guardian . Consultado el 31 de octubre de 2016 .
- ^ Broug, Eric (2008). Patrones geométricos islámicos . Thames and Hudson . Págs. 22-23 y siguientes. ISBN 978-0-500-28721-7.
- ^ Katz, Eugene A.; Jin, Bih-Yaw (agosto de 2016). Huylebrouck, Dirk (ed.). "Fullerenos, poliedros y leones guardianes chinos". El turista matemático. The Mathematical Intelligencer . 38 (3): 61–68. doi :10.1007/s00283-016-9663-0.
- ^ Hans Ulrich Instinsky: Der spätrömische Silberschatzfund von Kaiseraugst. Maguncia 1971, placa 85.
- ^ Los pavimentos Cosmati en la Abadía de Westminster. Consultado el 14 de septiembre de 2013.
- ^ Codex Atlanticus , foll. 307r–309v, 459r (datados entre 1478 y 1519).
- ^ Bartfeld, Martha (2005). Cómo crear mandalas de geometría sagrada . Santa Fe, NM: Mandalart Creations. pág. 35. ISBN 9780966228526.OCLC 70293628 .
- ^ Weisstein, Eric W. (12 de diciembre de 2002). CRC Concise Encyclopedia of Mathematics, segunda edición. CRC Press (publicado en 2002). pág. 1079. ISBN 1420035223.
- ^ Eg Zaman, Sana (14 de mayo de 2013). "Zaeem Jamal lanza una nueva colección a bordo de un yate privado en Dubai Marina". Haute Living . Consultado el 9 de noviembre de 2015 .
- ^ Cooper, Ed (25 de febrero de 2013). «Bring Me The Horizon: Este álbum tiene que ser el que dure para siempre». The Independent . Archivado desde el original el 23 de octubre de 2015. Consultado el 8 de noviembre de 2015 .
- ^ Denham, Jess (6 de noviembre de 2015). «Nuevo álbum de Coldplay: Beyoncé y Noel Gallagher participarán en A Head Full of Dreams» . The Independent . Archivado desde el original el 24 de mayo de 2022 . Consultado el 8 de noviembre de 2015 .
- ^ "Il significato del simbolo del Sole delle Alpi" (en italiano). Liga Norte. Archivado desde el original el 12 de enero de 2014 . Consultado el 1 de diciembre de 2014 .
- ↑ Ivano Dorboló (6 de junio de 2010). "La iglesia de S.Egidio y el símbolo del Sol de los Alpes". Historia de Confine – Valli di Natisone . Consultado el 9 de noviembre de 2015 .
- ^ Empaquetamientos de esferas, redes y grupos , John Conway, Neil JA Sloane, Capítulo 2, sección 1.1, Cobertura del espacio con círculos superpuestos. págs. 31-32. Figura 2.1 Cobertura del plano con círculos (b) La cobertura más eficiente o más delgada en una red hexagonal. [1]
- ^ Matemáticas mesopotámicas 2100-1600 a. C.: constantes técnicas en la burocracia y la educación (Ediciones Oxford de textos cuneiformes), Eleanor Robson, Clarendon Press, 1999, ISBN 978-0198152460 [2] en books.google.com
- ^ Creación de cuadrículas cuadradas a partir de círculos
Enlaces externos
- Weisstein, Eric W. "Intersección círculo-círculo". MathWorld .
- El artículo de La Flor de la Vida de The Mystica











.jpg/440px-Coffee_cup_with_overlapping_circles_grid_ornament_(Germany,_2022).jpg)







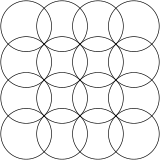




![La cuadrícula de cinco círculos superpuestos relacionada se construye a partir de dos conjuntos de círculos superpuestos con un desplazamiento medio.[22]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/ea/Square_five_overlapping_circle_grid.svg/120px-Square_five_overlapping_circle_grid.svg.png)

