Filtro de guía de ondas

Un filtro de guía de ondas es un filtro electrónico construido con tecnología de guía de ondas . Las guías de ondas son conductos metálicos huecos dentro de los cuales se puede transmitir una onda electromagnética . Los filtros son dispositivos que se utilizan para permitir el paso de señales en algunas frecuencias (la banda de paso ), mientras que otras son rechazadas (la banda de rechazo ). Los filtros son un componente básico de los diseños de ingeniería electrónica y tienen numerosas aplicaciones. Estas incluyen la selección de señales y la limitación del ruido . Los filtros de guía de ondas son más útiles en la banda de frecuencias de microondas , donde tienen un tamaño conveniente y una pérdida baja . Se encuentran ejemplos del uso de filtros de microondas en comunicaciones por satélite , redes telefónicas y transmisión de televisión .

Los filtros de guía de ondas se desarrollaron durante la Segunda Guerra Mundial para satisfacer las necesidades de los radares y las contramedidas electrónicas , pero después encontraron aplicaciones civiles, como su uso en enlaces de microondas . Gran parte del desarrollo de la posguerra se centró en reducir el volumen y el peso de estos filtros, primero mediante el uso de nuevas técnicas de análisis que llevaron a la eliminación de componentes innecesarios, luego mediante innovaciones como cavidades de modo dual y materiales novedosos como resonadores cerámicos .

Una característica particular del diseño de los filtros de guía de ondas se refiere al modo de transmisión. Los sistemas basados ​​en pares de cables conductores y tecnologías similares tienen un solo modo de transmisión. En los sistemas de guía de ondas, es posible cualquier número de modos. Esto puede ser tanto una desventaja, ya que los modos espurios causan problemas con frecuencia, como una ventaja, ya que un diseño de modo dual puede ser mucho más pequeño que el diseño monomodo de guía de ondas equivalente. Las principales ventajas de los filtros de guía de ondas sobre otras tecnologías son su capacidad para manejar alta potencia y su baja pérdida. Las principales desventajas son su volumen y costo en comparación con tecnologías como los filtros de microbanda .

Existe una amplia gama de diferentes tipos de filtros de guía de ondas. Muchos de ellos consisten en una cadena de resonadores acoplados de algún tipo que se puede modelar como una red en escalera de circuitos LC . Uno de los tipos más comunes consiste en una serie de cavidades resonantes acopladas . Incluso dentro de este tipo, hay muchos subtipos, principalmente diferenciados por los medios de acoplamiento . Estos tipos de acoplamiento incluyen aperturas, iris ^[w] , ^[x] y postes. Otros tipos de filtros de guía de ondas incluyen filtros resonadores dieléctricos , filtros de inserción, filtros de línea fina, filtros de guía de ondas corrugadas y filtros stub. Una serie de componentes de guía de ondas tienen teoría de filtros aplicada a su diseño, pero su propósito es algo más que filtrar señales. Dichos dispositivos incluyen componentes de adaptación de impedancia , acopladores direccionales y diplexores . Estos dispositivos frecuentemente toman la forma de un filtro, al menos en parte.

El significado común de guía de ondas , cuando el término se usa sin reservas, es el tipo de metal hueco (u ocasionalmente lleno de dieléctrico ), pero son posibles otras tecnologías de guía de ondas. ^[1] El alcance de este artículo se limita al tipo de conducto metálico. La estructura de guía de ondas de pared posterior es una variante, pero está lo suficientemente relacionada como para incluirla en este artículo: la onda está rodeada principalmente por material conductor. Es posible construir guías de ondas a partir de varillas dieléctricas , ^[2] el ejemplo más conocido son las fibras ópticas . Este tema está fuera del alcance del artículo con la excepción de que los resonadores de varillas dieléctricas a veces se usan dentro de guías de ondas de metal hueco. Las tecnologías de línea de transmisión ^[o] como los cables conductores y la microbanda pueden considerarse guías de ondas, ^[3] pero no se las llama comúnmente así y también están fuera del alcance de este artículo.

En electrónica , los filtros se utilizan para permitir el paso de señales de una determinada banda de frecuencias y bloquear otras. Son un elemento básico de los sistemas electrónicos y tienen una gran cantidad de aplicaciones. Entre los usos de los filtros de guía de ondas se encuentran la construcción de duplexores, diplexores y multiplexores ; la selectividad y ^limitación de ruido en receptores ; y la supresión de distorsión armónica en transmisores . ^[4]

Las guías de ondas son conductos metálicos que se utilizan para confinar y dirigir las señales de radio. Suelen estar hechas de latón, pero también se utilizan aluminio y cobre. ^[5] Lo más habitual es que sean rectangulares, pero también pueden tener otras secciones transversales , como circulares o elípticas. Un filtro de guía de ondas es un filtro compuesto por componentes de guía de ondas. Tiene una gama de aplicaciones muy similar a otras tecnologías de filtrado en electrónica e ingeniería de radio, pero es muy diferente mecánicamente y en su principio de funcionamiento. ^[6]

La tecnología utilizada para construir filtros se elige en gran medida por la frecuencia de operación que se espera, aunque existe una gran cantidad de superposición. Las aplicaciones de baja frecuencia, como la electrónica de audio, utilizan filtros compuestos de condensadores e inductores discretos . En algún lugar de la banda de frecuencia muy alta , los diseñadores cambian al uso de componentes hechos de trozos de línea de transmisión. ^[p] Este tipo de diseños se denominan filtros de elementos distribuidos . Los filtros hechos de componentes discretos a veces se denominan filtros de elementos concentrados para distinguirlos. A frecuencias aún más altas, las bandas de microondas , el diseño cambia a filtros de guía de ondas o, a veces, a una combinación de guías de ondas y líneas de transmisión. ^[7]

Los filtros de guía de ondas tienen mucho más en común con los filtros de línea de transmisión que los filtros de elementos concentrados; no contienen ningún condensador o inductor discreto. Sin embargo, el diseño de la guía de ondas puede ser con frecuencia equivalente (o aproximadamente equivalente) a un diseño de elementos concentrados. De hecho, el diseño de filtros de guía de ondas con frecuencia comienza a partir de un diseño de elementos concentrados y luego convierte los elementos de ese diseño en componentes de guía de ondas. ^[8]

Una de las diferencias más importantes en el funcionamiento de los filtros de guía de ondas en comparación con los diseños de líneas de transmisión se refiere al modo de transmisión de la onda electromagnética que transporta la señal. En una línea de transmisión, la onda está asociada a corrientes eléctricas en un par de conductores. Los conductores limitan las corrientes para que sean paralelas a la línea y, en consecuencia, tanto los componentes magnéticos como eléctricos del campo electromagnético son perpendiculares a la dirección de propagación de la onda. Este modo transversal se designa TEM ^[l] (transversal electromagnético). Por otro lado, hay infinitos modos que cualquier guía de ondas completamente hueca puede soportar, pero el modo TEM no es uno de ellos. Los modos de guía de ondas se designan TE ^[m] (transversal eléctrico) o TM ^[n] (transversal magnético), seguidos de un par de sufijos que identifican el modo preciso. ^[9]

Esta multiplicidad de modos puede causar problemas en los filtros de guía de ondas cuando se generan modos espurios. Los diseños suelen basarse en un solo modo y con frecuencia incorporan funciones para suprimir los modos no deseados. Por otro lado, se puede obtener ventaja eligiendo el modo correcto para la aplicación e incluso a veces haciendo uso de más de un modo a la vez. Cuando solo se utiliza un solo modo, la guía de ondas se puede modelar como una línea de transmisión conductora y se pueden aplicar los resultados de la teoría de líneas de transmisión. ^[10]

Otra característica peculiar de los filtros de guía de ondas es que existe una frecuencia definida, la frecuencia de corte , por debajo de la cual no puede tener lugar ninguna transmisión. Esto significa que, en teoría, no se pueden hacer filtros de paso bajo en guías de ondas. Sin embargo, los diseñadores frecuentemente toman un diseño de filtro de paso bajo de elementos concentrados y lo convierten en una implementación de guía de ondas. En consecuencia, el filtro es de paso bajo por diseño y puede considerarse un filtro de paso bajo para todos los fines prácticos si la frecuencia de corte está por debajo de cualquier frecuencia de interés para la aplicación. La frecuencia de corte de la guía de ondas es una función del modo de transmisión, por lo que a una frecuencia dada, la guía de ondas puede ser utilizable en algunos modos pero no en otros. Del mismo modo, la longitud de onda de la guía ^[h] (λ _g ) y la impedancia característica ^[b] ( Z ₀ ) de la guía a una frecuencia dada también dependen del modo. ^[11]

El modo con la frecuencia de corte más baja de todos los modos se denomina modo dominante. Entre el modo de corte y el siguiente modo más alto, este es el único modo que es posible transmitir, por lo que se lo describe como dominante. Cualquier modo espurio generado se atenúa rápidamente a lo largo de la guía y desaparece pronto. Los diseños prácticos de filtros se realizan con frecuencia para operar en el modo dominante. ^[12]

En la guía de onda rectangular, el modo TE ₁₀ ^[q] (mostrado en la figura 2) es el modo dominante. Hay una banda de frecuencias entre el corte del modo dominante y el siguiente corte del modo más alto en el que la guía de onda puede funcionar sin ninguna posibilidad de generar modos espurios. Los siguientes modos de corte más altos son TE ₂₀ [ r ^] exactamente al doble del modo TE _{10 , y TE 01} ^[s] que también es el doble de TE ₁₀ si la guía de onda utilizada tiene la relación de aspecto comúnmente utilizada de 2:1. El modo TM de corte más bajo es TM ₁₁ ^[t] (mostrado en la figura 2) que es 2 veces el modo dominante en la guía de onda 2:1. Por lo tanto, hay una octava sobre la cual el modo dominante está libre de modos espurios, aunque generalmente se evita operar demasiado cerca del corte debido a la distorsión de fase. ^[13]${\displaystyle \scriptstyle {\sqrt {5}}}$

En la guía de onda circular, el modo dominante es TE ₁₁ ^[u] y se muestra en la figura 2. El siguiente modo más alto es TM _01. ^[v] El rango en el que se garantiza que el modo dominante esté libre de modos espurios es menor que en la guía de onda rectangular; la relación entre la frecuencia más alta y la más baja es aproximadamente 1,3 en la guía de onda circular, en comparación con 2,0 en la guía rectangular. ^[14]

Los modos evanescentes son modos que se encuentran por debajo de la frecuencia de corte. No pueden propagarse a lo largo de la guía de ondas a ninguna distancia y se desvanecen exponencialmente. Sin embargo, son importantes para el funcionamiento de ciertos componentes de filtros como los iris y los postes, que se describen más adelante, porque la energía se almacena en los campos de ondas evanescentes. ^[15]

Al igual que los filtros de línea de transmisión, los filtros de guía de ondas siempre tienen múltiples bandas de paso , réplicas del prototipo de elemento concentrado . En la mayoría de los diseños, solo la banda de paso de frecuencia más baja es útil (o las dos más bajas en el caso de los filtros de rechazo de banda ) y el resto se consideran artefactos espurios no deseados. Esta es una propiedad intrínseca de la tecnología y no se puede diseñar para eliminarla, aunque el diseño puede tener cierto control sobre la posición de frecuencia de las bandas espurias. En consecuencia, en cualquier diseño de filtro dado, existe una frecuencia superior más allá de la cual el filtro no podrá llevar a cabo su función. Por esta razón, los verdaderos filtros de paso bajo y paso alto no pueden existir en la guía de ondas. En alguna frecuencia alta habrá una banda de paso o rechazo espuria que interrumpa la función prevista del filtro. Pero, de manera similar a la situación con la frecuencia de corte de la guía de ondas, el filtro se puede diseñar de modo que el borde de la primera banda espuria esté muy por encima de cualquier frecuencia de interés. ^[16]

El rango de frecuencias en el que son útiles los filtros de guía de ondas está determinado en gran medida por el tamaño de guía de ondas necesario. A frecuencias más bajas, la guía de ondas debe ser demasiado grande para mantener la frecuencia de corte por debajo de la frecuencia operativa. Por otro lado, los filtros cuyas frecuencias operativas son tan altas que las longitudes de onda son submilimétricas no se pueden fabricar con procesos de taller normales . A frecuencias tan altas, la tecnología de fibra óptica comienza a convertirse en una opción. ^[17]

Las guías de ondas son un medio de baja pérdida. Las pérdidas en las guías de ondas provienen principalmente de la disipación óhmica causada por corrientes inducidas en las paredes de la guía de ondas. La guía de ondas rectangular tiene una pérdida menor que la guía de ondas circular y suele ser el formato preferido, pero el modo circular TE ₀₁ tiene una pérdida muy baja y tiene aplicaciones en comunicaciones de larga distancia. Las pérdidas se pueden reducir puliendo las superficies internas de las paredes de la guía de ondas. En algunas aplicaciones que requieren un filtrado riguroso, las paredes se recubren con una fina capa de oro o plata para mejorar la conductividad de la superficie . Un ejemplo de tales requisitos son las aplicaciones satelitales que requieren bajas pérdidas, alta selectividad y retardo de grupo lineal de sus filtros. ^[18]

Una de las principales ventajas de los filtros de guía de onda sobre las tecnologías de modo TEM es la calidad de sus resonadores . La calidad del resonador se caracteriza por un parámetro llamado factor Q , o simplemente Q. El Q de los resonadores de guía de onda se encuentra en los miles, órdenes de magnitud más altos que los resonadores de modo TEM. ^[19] La resistencia de los conductores, especialmente en inductores bobinados, limita el Q de los resonadores TEM. Esta mejora de Q conduce a filtros de mejor rendimiento en guías de onda, con mayor rechazo de banda de detención. La limitación de Q en guías de onda proviene principalmente de las pérdidas óhmicas en las paredes descritas anteriormente, pero el recubrimiento de plata de las paredes internas puede más que duplicar Q. ^[20]

Las guías de ondas tienen una buena capacidad de manejo de potencia, lo que conduce a aplicaciones de filtros en radares . ^[21] A pesar de las ventajas de rendimiento de los filtros de guías de ondas, la microbanda es a menudo la tecnología preferida debido a su bajo costo. Esto es especialmente cierto para los artículos de consumo y las frecuencias de microondas más bajas. Los circuitos de microbanda se pueden fabricar mediante tecnología de circuito impreso barata y, cuando se integran en la misma placa impresa que otros bloques de circuitos, incurren en un pequeño costo adicional. ^[22]

La idea de una guía de ondas para ondas electromagnéticas fue sugerida por primera vez por Lord Rayleigh en 1897. Rayleigh propuso que una línea de transmisión coaxial podría tener el conductor central eliminado, y las ondas seguirían propagándose por el interior del conductor cilíndrico restante a pesar de que ya no hubiera un circuito eléctrico completo de conductores. Describió esto en términos de la onda reflejándose repetidamente en la pared interna del conductor externo en forma de zigzag a medida que avanzaba por la guía de ondas. Rayleigh también fue el primero en darse cuenta de que había una longitud de onda crítica, la longitud de onda de corte, proporcional al diámetro del cilindro, por encima de la cual la propagación de ondas no es posible. Sin embargo, el interés en las guías de ondas disminuyó porque las frecuencias más bajas eran más adecuadas para la comunicación por radio de larga distancia. Los resultados de Rayleigh fueron olvidados por un tiempo y tuvieron que ser redescubiertos por otros en la década de 1930, cuando resurgió el interés por las microondas. Las guías de ondas fueron desarrolladas por primera vez, en forma circular, por George Clark Southworth y JF Hargreaves en 1932. ^[23]

El primer diseño de filtro analógico que fue más allá de un simple resonador único fue creado por George Ashley Campbell en 1910 y marcó el comienzo de la teoría de filtros. El filtro de Campbell era un diseño de elementos concentrados de condensadores e inductores sugerido por su trabajo con bobinas de carga . Otto Zobel y otros rápidamente lo desarrollaron más. ^{[24] El desarrollo de filtros de elementos distribuidos comenzó en los años anteriores a la Segunda Guerra Mundial.} Mason y Sykes publicaron un importante artículo sobre el tema en 1937; ^[25] una patente ^[26] presentada por Mason en 1927 puede contener el primer diseño de filtro publicado que utiliza elementos distribuidos. ^[27]

El trabajo de Mason y Sykes se centró en los formatos de cable coaxial y pares de cables balanceados, pero otros investigadores aplicaron posteriormente los principios también a las guías de ondas. Gran parte del desarrollo de los filtros de guía de ondas se llevó a cabo durante la Segunda Guerra Mundial impulsado por las necesidades de filtrado del radar y las contramedidas electrónicas . Una buena parte de esto se realizó en el Laboratorio de Radiación del MIT (Rad Lab), pero también participaron otros laboratorios de los EE. UU. y el Reino Unido, como el Telecommunications Research Establishment en el Reino Unido. Entre los científicos e ingenieros conocidos del Rad Lab se encontraban Julian Schwinger , Nathan Marcuvitz , Edward Mills Purcell y Hans Bethe . Bethe solo estuvo en el Rad Lab un corto tiempo, pero produjo su teoría de apertura mientras estaba allí. La teoría de apertura es importante para los filtros de cavidad de guía de ondas, que se desarrollaron por primera vez en el Rad Lab. Su trabajo se publicó después de la guerra en 1948 e incluye una descripción temprana de las cavidades de modo dual por Fano y Lawson. ^[28]

El trabajo teórico posterior a la guerra incluyó la teoría de líneas conmensurables de Paul Richards . Las líneas conmensurables son redes en las que todos los elementos tienen la misma longitud (o en algunos casos múltiplos de la longitud unitaria), aunque pueden diferir en otras dimensiones para dar diferentes impedancias características. ^[a] La transformación de Richards permite que cualquier diseño de elemento agrupado se tome "tal cual" y se transforme directamente en un diseño de elemento distribuido utilizando una ecuación de transformación muy simple. En 1955, K. Kuroda publicó las transformaciones conocidas como identidades de Kuroda . Estas hicieron que el trabajo de Richard fuera más utilizable en formatos desequilibrados y de guía de ondas al eliminar los problemáticos elementos conectados en serie , pero pasó algún tiempo antes de que el trabajo japonés de Kuroda se hiciera ampliamente conocido en el mundo de habla inglesa. ^[29] Otro desarrollo teórico fue el enfoque del filtro de síntesis de red de Wilhelm Cauer en el que utilizó la aproximación de Chebyshev para determinar los valores de los elementos. El trabajo de Cauer se desarrolló en gran parte durante la Segunda Guerra Mundial (Cauer murió hacia el final de la misma), pero no pudo publicarse ampliamente hasta que terminaron las hostilidades. Si bien el trabajo de Cauer se refiere a elementos agrupados, es de cierta importancia para los filtros de guía de ondas; el filtro de Chebyshev , un caso especial de la síntesis de Cauer, se usa ampliamente como un filtro prototipo para diseños de guías de ondas. ^[30]

Los diseños de la década de 1950 comenzaron con un prototipo de elemento concentrado (una técnica que todavía se usa hoy en día) y, después de varias transformaciones, se llegó al filtro deseado en forma de guía de ondas. En ese momento, este enfoque producía anchos de banda fraccionarios de no más de ⁠1/5En 1957 , Leo Young, del Stanford Research Institute, publicó un método para diseñar filtros que comenzaba con un prototipo de elemento distribuido, el prototipo de impedancia escalonada. Este filtro se basaba en transformadores de impedancia de cuarto de onda de varios anchos y era capaz de producir diseños con anchos de banda de hasta una octava (un ancho de banda fraccionario de ⁠2/3⁠ ). El artículo de Young aborda específicamente los resonadores de cavidad acoplados directamente, pero el procedimiento puede aplicarse igualmente a otros tipos de resonadores acoplados directamente. ^[31]

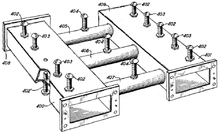
El primer relato publicado de un filtro acoplado de forma cruzada se debe a John R. Pierce de Bell Labs en una patente de 1948. ^[32] Un filtro acoplado de forma cruzada es aquel en el que se acoplan resonadores que no están inmediatamente adyacentes. Los grados de libertad adicionales que se proporcionan de esta manera permiten al diseñador crear filtros con un rendimiento mejorado o, alternativamente, con menos resonadores. Una versión del filtro de Pierce, que se muestra en la figura 3, utiliza resonadores de cavidad de guía de ondas circulares para conectar entre sí resonadores de cavidad de guía rectangulares. Este principio no fue muy utilizado al principio por los diseñadores de filtros de guía de ondas, pero fue ampliamente utilizado por los diseñadores de filtros mecánicos en la década de 1960, en particular por RA Johnson de Collins Radio Company . ^[33]

La primera aplicación no militar de los filtros de guía de ondas fue en los enlaces de microondas que utilizaban las empresas de telecomunicaciones para proporcionar la columna vertebral de sus redes. Estos enlaces también los utilizaban otras industrias con grandes redes fijas, en particular las emisoras de televisión. Estas aplicaciones formaban parte de grandes programas de inversión de capital. Ahora también se utilizan en sistemas de comunicaciones por satélite . ^[34]

La necesidad de un retardo independiente de la frecuencia en las aplicaciones satelitales condujo a una mayor investigación sobre la encarnación de guías de ondas de filtros acoplados de forma cruzada. Anteriormente, los sistemas de comunicaciones satelitales utilizaban un componente separado para la ecualización del retardo . Los grados de libertad adicionales obtenidos a partir de filtros acoplados de forma cruzada ofrecían la posibilidad de diseñar un retardo plano en un filtro sin comprometer otros parámetros de rendimiento. Un componente que funcionara simultáneamente como filtro y ecualizador ahorraría peso y espacio valiosos. Las necesidades de las comunicaciones satelitales también impulsaron la investigación sobre los modos de resonador más exóticos en la década de 1970. De particular importancia a este respecto es el trabajo de EL Griffin y FA Young, quienes investigaron mejores modos para la banda de 12-14 GHz cuando esta comenzó a usarse para satélites a mediados de la década de 1970. ^[35]

Otra innovación que permitió ahorrar espacio fue el resonador dieléctrico , que puede utilizarse en otros formatos de filtro además de en guías de ondas. El primer uso de estos en un filtro lo realizó SB Cohn en 1965, utilizando dióxido de titanio como material dieléctrico. Sin embargo, los resonadores dieléctricos utilizados en la década de 1960 tenían coeficientes de temperatura muy pobres, típicamente 500 veces peores que un resonador mecánico hecho de invar , lo que conducía a la inestabilidad de los parámetros del filtro. Los materiales dieléctricos de la época con mejores coeficientes de temperatura tenían una constante dieléctrica demasiado baja para ser útiles para ahorrar espacio. Esto cambió con la introducción de resonadores cerámicos con coeficientes de temperatura muy bajos en la década de 1970. El primero de ellos fue de Massé y Pucel, que utilizó tetratitanato de bario ^{[nota 1]} en Raytheon en 1972. Bell Labs y Murata Manufacturing informaron de más mejoras en 1979 . El resonador de nonatitanato de bario de Bell Labs ^{[nota 2]} tenía una constante dieléctrica de 40 y un Q de 5000-10 000 a 2-7 GHz . Los materiales modernos estables a la temperatura tienen una constante dieléctrica de aproximadamente 90 a frecuencias de microondas, pero la investigación continúa para encontrar materiales con baja pérdida y alta permitividad; los materiales de menor permitividad, como el titanato de estannato de circonio ^{[nota 3]} (ZST) con una constante dieléctrica de 38, todavía se utilizan a veces por su propiedad de baja pérdida. ^[36]

Un enfoque alternativo para diseñar filtros de guía de ondas más pequeños fue el uso de modos evanescentes no propagadores. Jaynes y Edson propusieron filtros de guía de ondas de modo evanescente a fines de la década de 1950. Craven y Young crearon métodos para diseñar estos filtros en 1966. Desde entonces, los filtros de guía de ondas de modo evanescente se han utilizado con éxito cuando el tamaño o el peso de la guía de ondas son consideraciones importantes. ^[37]

Una tecnología relativamente reciente que se utiliza en el interior de los filtros de guía de ondas de metal hueco es la finline, un tipo de guía de ondas dieléctrica plana. La finline fue descrita por primera vez por Paul Meier en 1972. ^[38]

Los multiplexores fueron descritos por primera vez por Fano y Lawson en 1948. Pierce fue el primero en describir multiplexores con bandas de paso contiguas. La multiplexación mediante filtros direccionales fue inventada por Seymour Cohn y Frank Coale en la década de 1950. Los multiplexores con resonadores de inmitancia compensadores en cada unión son en gran parte el trabajo de EG Cristal y GL Matthaei en la década de 1960. Esta técnica todavía se utiliza a veces, pero la disponibilidad moderna de potencia de cálculo ha llevado al uso más común de técnicas de síntesis que pueden producir directamente filtros coincidentes sin la necesidad de estos resonadores adicionales. En 1965, RJ Wenzel descubrió que los filtros que tenían una terminación simple, ^[k] en lugar de la habitual terminación doble, eran complementarios, exactamente lo que se necesitaba para un diplexor. ^[c] Wenzel se inspiró en las conferencias del teórico de circuitos Ernst Guillemin . ^[39]

Harold Schumacher, de Microphase Corporation, investigó los multiplexores multicanal y multioctava, y sus resultados se publicaron en 1976. El principio de que los filtros multiplexores pueden emparejarse cuando se unen modificando los primeros elementos, eliminando así los resonadores de compensación, fue descubierto accidentalmente por EJ Curly alrededor de 1968, cuando desintonizó un diplexor. JD Rhodes proporcionó una teoría formal para esto en 1976 y Rhodes y Ralph Levy la generalizaron a los multiplexores en 1979. ^[40]

A partir de la década de 1980, las tecnologías planares, especialmente las microbandas, han tendido a sustituir a otras tecnologías utilizadas para la construcción de filtros y multiplexores, especialmente en productos destinados al mercado de consumo. La reciente innovación de las guías de onda post-wall permite implementar diseños de guías de onda sobre un sustrato plano con técnicas de fabricación de bajo coste similares a las utilizadas para las microbandas. ^[41]

Los diseños de filtros de guía de ondas con frecuencia constan de dos componentes diferentes que se repiten varias veces. Normalmente, un componente es un resonador o discontinuidad con un circuito agrupado equivalente a un inductor, un condensador o un circuito resonante LC. A menudo, el tipo de filtro tomará su nombre del estilo de este componente. Estos componentes están separados por un segundo componente, una longitud de guía que actúa como un transformador de impedancia. Los transformadores de impedancia tienen el efecto de hacer que las instancias alternativas del primer componente parezcan ser de una impedancia diferente. El resultado neto es un circuito equivalente de elementos agrupados de una red en escalera. Los filtros de elementos agrupados suelen tener topología en escalera , y un circuito de este tipo es un punto de partida típico para los diseños de filtros de guía de ondas. La figura 4 muestra una escalera de este tipo. Normalmente, los componentes de la guía de ondas son resonadores, y el circuito equivalente serían resonadores LC en lugar de los condensadores e inductores que se muestran, pero los circuitos como el de la figura 4 todavía se utilizan como filtros prototipo con el uso de una transformación de paso de banda o de eliminación de banda. ^[42]

Los parámetros de rendimiento del filtro, como el rechazo de la banda de rechazo y la velocidad de transición entre la banda de paso y la banda de rechazo, se mejoran añadiendo más componentes y aumentando así la longitud del filtro. Cuando los componentes se repiten de forma idéntica, el filtro es un diseño de filtro de parámetros de imagen y el rendimiento se mejora simplemente añadiendo más elementos idénticos. Este enfoque se utiliza normalmente en diseños de filtros que utilizan una gran cantidad de elementos muy espaciados, como el filtro de hierro de gofres . Para diseños en los que los elementos están más espaciados, se pueden obtener mejores resultados utilizando un diseño de filtro de síntesis de red, como el filtro común de Chebyshev y los filtros Butterworth . En este enfoque, los elementos del circuito no tienen todos el mismo valor y, en consecuencia, los componentes no tienen todos las mismas dimensiones. Además, si el diseño se mejora añadiendo más componentes, todos los valores de los elementos deben calcularse de nuevo desde cero. En general, no habrá valores comunes entre las dos instancias del diseño. Los filtros de guía de ondas de Chebyshev se utilizan cuando los requisitos de filtrado son rigurosos, como las aplicaciones satelitales. ^{[43] [44]}

Un transformador de impedancia es un dispositivo que hace que una impedancia en su puerto de salida aparezca como una impedancia diferente en su puerto de entrada. En una guía de ondas, este dispositivo es simplemente una longitud corta de guía de ondas. Especialmente útil es el transformador de impedancia de cuarto de onda que tiene una longitud de λ _g /4. Este dispositivo puede convertir capacitancias en inductancias y viceversa. ^[45] También tiene la propiedad útil de convertir elementos conectados en derivación en elementos conectados en serie y viceversa. Los elementos conectados en serie son de otro modo difíciles de implementar en una guía de ondas. ^[46]

Muchos componentes de filtros de guías de ondas funcionan introduciendo un cambio repentino, una discontinuidad, en las propiedades de transmisión de la guía de ondas. Dichas discontinuidades son equivalentes a elementos de impedancia concentrados colocados en ese punto. Esto surge de la siguiente manera: la discontinuidad provoca una reflexión parcial de la onda transmitida hacia abajo por la guía en la dirección opuesta, la relación entre los dos se conoce como coeficiente de reflexión . Esto es completamente análogo a una reflexión en una línea de transmisión donde existe una relación establecida entre el coeficiente de reflexión y la impedancia que causó la reflexión. Esta impedancia debe ser reactiva , es decir, debe ser una capacitancia o una inductancia. No puede ser una resistencia ya que no se ha absorbido energía; toda se transmite hacia adelante o se refleja. Los ejemplos de componentes con esta función incluyen irises, stubs y postes, todos descritos más adelante en este artículo bajo los tipos de filtro en los que se encuentran. ^[47]

Un escalón de impedancia es un ejemplo de un dispositivo que introduce una discontinuidad. Se logra mediante un cambio escalonado en las dimensiones físicas de la guía de ondas. Esto da como resultado un cambio escalonado en la impedancia característica de la guía de ondas. El escalón puede ser en el plano E ^[f] (cambio de altura ^[j] ) o en el plano H ^[g] (cambio de ancho ^[i] ) de la guía de ondas. ^[48]

Un componente básico de los filtros de guía de ondas es el resonador de cavidad . Este consiste en una pequeña longitud de guía de ondas bloqueada en ambos extremos. Las ondas atrapadas dentro del resonador se reflejan de ida y vuelta entre los dos extremos. Una geometría dada de cavidad resonará a una frecuencia característica. El efecto de resonancia se puede utilizar para pasar selectivamente ciertas frecuencias. Su uso en una estructura de filtro requiere que se permita que parte de la onda pase de una cavidad a otra a través de una estructura de acoplamiento. Sin embargo, si la abertura en el resonador se mantiene pequeña, entonces un enfoque de diseño válido es diseñar la cavidad como si estuviera completamente cerrada y los errores serán mínimos. Se utilizan varios mecanismos de acoplamiento diferentes en diferentes clases de filtro. ^[49]

La nomenclatura de los modos en una cavidad introduce un tercer índice, por ejemplo TE ₀₁₁ . Los dos primeros índices describen la onda que se desplaza hacia arriba y hacia abajo a lo largo de la cavidad, es decir, son los números de modo transversales como para los modos en una guía de ondas. El tercer índice describe el modo longitudinal causado por el patrón de interferencia de las ondas que se desplazan hacia adelante y las reflejadas. El tercer índice es igual al número de medias longitudes de onda a lo largo de la guía. Los modos más comunes utilizados son los modos dominantes: TE ₁₀₁ en guía de ondas rectangular y TE ₁₁₁ en guía de ondas circular. El modo circular TE ₀₁₁ se utiliza cuando se requiere una pérdida muy baja (por lo tanto, un Q alto ) pero no se puede utilizar en un filtro de modo dual porque es circularmente simétrico. Los mejores modos para la guía de ondas rectangular en filtros de modo dual son TE ₁₀₃ y TE ₁₀₅ . Sin embargo, aún mejor es el modo de guía de ondas circular TE ₁₁₃ que puede lograr un Q de 16.000 a 12 GHz . ^[50]

Los tornillos de ajuste son tornillos insertados en cavidades resonantes que se pueden ajustar externamente a la guía de ondas. Proporcionan un ajuste fino de la frecuencia resonante insertando más o menos rosca en la guía de ondas. Se pueden ver ejemplos en el filtro posterior de la figura 1: cada cavidad tiene un tornillo de ajuste asegurado con tuercas de seguridad y compuesto de bloqueo de roscas . Para tornillos insertados solo una distancia pequeña, el circuito equivalente es un condensador en derivación, que aumenta en valor a medida que se inserta el tornillo. Sin embargo, cuando el tornillo se ha insertado una distancia λ/4, resuena equivalente a un circuito LC en serie. Insertarlo aún más hace que la impedancia cambie de capacitiva a inductiva, es decir, cambia el signo aritmético. ^[51]

Un iris es una placa metálica delgada que atraviesa la guía de ondas y tiene uno o más orificios. Se utiliza para acoplar dos longitudes de guía de ondas y es un medio para introducir una discontinuidad. Algunas de las posibles geometrías de los iris se muestran en la figura 5. Un iris que reduce el ancho de una guía de ondas rectangular tiene un circuito equivalente a una inductancia en derivación, mientras que uno que restringe la altura es equivalente a una capacitancia en derivación. Un iris que restringe ambas direcciones es equivalente a un circuito resonante LC en paralelo . Se puede formar un circuito LC en serie espaciando la parte conductora del iris lejos de las paredes de la guía de ondas. Los filtros de banda estrecha utilizan frecuentemente iris con orificios pequeños. Estos siempre son inductivos independientemente de la forma del orificio o su posición en el iris. Los orificios circulares son fáciles de mecanizar, pero los orificios alargados, o los orificios en forma de cruz, son ventajosos para permitir la selección de un modo particular de acoplamiento. ^[52]

Los iris son una forma de discontinuidad y funcionan excitando modos superiores evanescentes. Los bordes verticales son paralelos al campo eléctrico (campo E) y excitan los modos TE. La energía almacenada en los modos TE se encuentra predominantemente en el campo magnético (campo H) y, en consecuencia, el equivalente concentrado de esta estructura es un inductor. Los bordes horizontales son paralelos al campo H y excitan los modos TM. En este caso, la energía almacenada se encuentra predominantemente en el campo E y el equivalente concentrado es un condensador. ^[53]

Es bastante sencillo fabricar diafragmas que se puedan ajustar mecánicamente. Se puede introducir y sacar una placa fina de metal a través de una ranura estrecha en el lateral de la guía de ondas. En ocasiones, se elige la construcción con diafragma por esta capacidad de fabricar un componente variable. ^[54]

Un filtro acoplado por iris consiste en una cascada de transformadores de impedancia en forma de cavidades resonantes de guía de ondas acopladas entre sí por iris. ^[43] En aplicaciones de alta potencia se evitan los iris capacitivos. La reducción de la altura de la guía de ondas (la dirección del campo E) hace que la intensidad del campo eléctrico a través del espacio aumente y se produzca un arco eléctrico (o ruptura dieléctrica si la guía de ondas está llena de un aislante) a una potencia menor de la que se produciría de otro modo. ^[55]

Los postes son barras conductoras, generalmente circulares, fijadas internamente a lo largo de la altura de la guía de ondas y son otro medio para introducir una discontinuidad. Un poste delgado tiene un circuito equivalente a un inductor en derivación. Una fila de postes puede considerarse como una forma de iris inductivo. ^[56]

Un filtro posterior consta de varias filas de postes a lo ancho de la guía de ondas que la separan en cavidades resonantes, como se muestra en la figura 7. Se pueden utilizar diferentes cantidades de postes en cada fila para lograr distintos valores de inductancia. Se puede ver un ejemplo en la figura 1. El filtro funciona de la misma manera que el filtro acoplado al iris, pero difiere en el método de construcción. ^[57]

Una guía de onda post-pared, o guía de onda integrada en sustrato, es un formato más reciente que busca combinar las ventajas de baja pérdida de radiación, alta Q y manejo de alta potencia de la guía de onda de tubo hueco de metal tradicional con el tamaño pequeño y la facilidad de fabricación de las tecnologías planares (como el formato de microbanda ampliamente utilizado). Consiste en un sustrato aislado perforado con dos filas de postes conductores que representan las paredes laterales de la guía de onda. La parte superior e inferior del sustrato están cubiertas con láminas conductoras, lo que hace que esta sea una construcción similar al formato de triple placa . Las técnicas de fabricación existentes de placa de circuito impreso o cerámica cocida a baja temperatura se pueden utilizar para hacer circuitos de guía de onda post-pared. Este formato se presta naturalmente a los diseños de filtro posterior de guía de onda. ^[58]

Un filtro de modo dual es un tipo de filtro de cavidad resonante, pero en este caso cada cavidad se utiliza para proporcionar dos resonadores empleando dos modos (dos polarizaciones), reduciendo así a la mitad el volumen del filtro para un orden determinado. Esta mejora en el tamaño del filtro es una ventaja importante en la aviónica de aeronaves y en aplicaciones espaciales. Los filtros de alta calidad en estas aplicaciones pueden requerir muchas cavidades que ocupan un espacio significativo. ^[59]

Los resonadores dieléctricos son piezas de material dieléctrico insertadas en la guía de ondas. Suelen ser cilíndricos, ya que se pueden fabricar sin mecanizar, pero se han utilizado otras formas. Se pueden fabricar con un orificio en el centro que se utiliza para fijarlos a la guía de ondas. No hay campo en el centro cuando se utiliza el modo circular TE ₀₁₁ , por lo que el orificio no tiene ningún efecto adverso. Los resonadores se pueden montar coaxiales a la guía de ondas, pero normalmente se montan transversalmente a lo ancho, como se muestra en la figura 8. Esta última disposición permite ajustar los resonadores insertando un tornillo a través de la pared de la guía de ondas en el orificio central del resonador. ^[60]

Cuando los resonadores dieléctricos están hechos de un material de alta permitividad , como uno de los titanatos de bario , tienen una importante ventaja de ahorro de espacio en comparación con los resonadores de cavidad. Sin embargo, son mucho más propensos a modos espurios. En aplicaciones de alta potencia, se pueden incorporar capas de metal en los resonadores para conducir el calor, ya que los materiales dieléctricos tienden a tener baja conductividad térmica . ^[61]

Los resonadores se pueden acoplar entre sí mediante iris o transformadores de impedancia. Alternativamente, se pueden colocar en una carcasa lateral con forma de casquillo y acoplarlos a través de una pequeña abertura. ^[62]

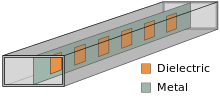
En los filtros de inserción, una o más láminas metálicas se colocan longitudinalmente a lo largo de la guía de ondas, como se muestra en la figura 9. Estas láminas tienen agujeros perforados para formar resonadores. El dieléctrico de aire proporciona a estos resonadores un Q alto . Se pueden utilizar varios insertos paralelos en la misma longitud de guía de ondas. Se pueden lograr resonadores más compactos con una lámina delgada de material dieléctrico y metalización impresa en lugar de agujeros en láminas metálicas a costa de un Q menor del resonador . ^[63]

Finline es un tipo diferente de tecnología de guía de ondas en la que las ondas en una tira delgada de dieléctrico están limitadas por dos tiras de metalización. Hay varias posibles disposiciones topológicas de las tiras de metal y dieléctrico. Finline es una variación de la guía de ondas de ranura, pero en el caso de Finline toda la estructura está encerrada en un blindaje metálico. Esto tiene la ventaja de que, al igual que la guía de ondas de metal hueca, no se pierde energía por radiación. Los filtros Finline se pueden hacer imprimiendo un patrón de metalización en una hoja de material dieléctrico y luego insertando la hoja en el plano E de una guía de ondas de metal hueca de manera similar a como se hace con los filtros de inserción. La guía de ondas de metal forma el blindaje para la guía de ondas Finline. Los resonadores se forman metalizando un patrón en la hoja dieléctrica. Se logran fácilmente patrones más complejos que el simple filtro de inserción de la figura 9 porque el diseñador no tiene que considerar el efecto sobre el soporte mecánico de la eliminación del metal. Esta complejidad no aumenta los costos de fabricación ya que la cantidad de procesos necesarios no cambia cuando se agregan más elementos al diseño. Los diseños de líneas finas son menos sensibles a las tolerancias de fabricación que los filtros de inserción y tienen anchos de banda amplios. ^[64]

Es posible diseñar filtros que funcionen internamente en su totalidad en modos evanescentes. Esto tiene ventajas de ahorro de espacio porque la guía de ondas del filtro, que a menudo forma la carcasa del filtro, no necesita ser lo suficientemente grande como para soportar la propagación del modo dominante. Normalmente, un filtro de modo evanescente consta de una longitud de guía de ondas más pequeña que la guía de ondas que alimenta los puertos de entrada y salida. En algunos diseños, esta puede doblarse para lograr un filtro más compacto. Se insertan tornillos de ajuste a intervalos específicos a lo largo de la guía de ondas, lo que produce capacitancias concentradas equivalentes en esos puntos. En diseños más recientes, los tornillos se reemplazan con insertos dieléctricos. Estos capacitores resuenan con la longitud anterior de la guía de ondas de modo evanescente que tiene el circuito equivalente de un inductor, produciendo así una acción de filtrado. La energía de muchos modos evanescentes diferentes se almacena en el campo alrededor de cada una de estas discontinuidades capacitivas. Sin embargo, el diseño es tal que solo el modo dominante llega al puerto de salida; los otros modos decaen mucho más rápidamente entre los capacitores. ^[65]

Los filtros de guía de onda corrugada , también llamados filtros de guía de onda con crestas , consisten en una serie de crestas, o dientes, que reducen periódicamente la altura interna de la guía de onda como se muestra en las figuras 10 y 11. Se utilizan en aplicaciones que requieren simultáneamente una banda de paso amplia, una buena adaptación de la banda de paso y una banda de supresión amplia. Son esencialmente diseños de paso bajo (por encima de la limitación habitual de la frecuencia de corte), a diferencia de la mayoría de las otras formas que suelen ser de paso de banda. La distancia entre los dientes es mucho menor que la distancia típica λ/4 entre elementos de otros diseños de filtros. Normalmente, se diseñan mediante el método de parámetros de imagen con todas las crestas idénticas, pero se pueden lograr otras clases de filtros como Chebyshev a cambio de la complejidad de fabricación. En el método de diseño de imagen, el circuito equivalente de las crestas se modela como una cascada de medias secciones LC . El filtro funciona en el modo TE ₁₀ dominante , pero los modos espurios pueden ser un problema cuando están presentes. En particular, hay poca atenuación de la banda de supresión de los modos TE ₂₀ y TE _30. ^[66]

El filtro de tipo waffle es una variante del filtro de guía de ondas corrugada. Tiene propiedades similares a las de ese filtro con la ventaja adicional de que se suprimen los modos TE ₂₀ y TE ₃₀ espurios . En el filtro de tipo waffle, se cortan canales a través de las crestas longitudinalmente hacia abajo del filtro. Esto deja una matriz de dientes que sobresalen internamente de las superficies superior e inferior de la guía de ondas. Este patrón de dientes se asemeja a una plancha de gofres , de ahí el nombre del filtro. ^[67]

Un stub es una pequeña longitud de guía de ondas conectada a algún punto del filtro en un extremo y en cortocircuito en el otro extremo. Los stubs en circuito abierto también son teóricamente posibles, pero una implementación en guía de ondas no es práctica porque la energía electromagnética se emitiría desde el extremo abierto del stub, lo que daría lugar a altas pérdidas. Los stubs son una especie de resonador, y el elemento concentrado equivalente es un circuito resonante LC. Sin embargo, en una banda estrecha, los stubs pueden considerarse como un transformador de impedancia. El cortocircuito se transforma en una inductancia o una capacitancia según la longitud del stub. ^[68]

Un filtro de guía de ondas se fabrica colocando uno o más extremos a lo largo de la longitud de una guía de ondas, generalmente separados λ _g /4, como se muestra en la figura 12. Los extremos de los extremos se tapan para cortocircuitarlos. ^[69] Cuando los extremos cortocircuitados tienen una longitud λ _g /4, el filtro será un filtro de rechazo de banda y los extremos tendrán un circuito equivalente aproximado de elementos concentrados de circuitos resonantes paralelos conectados en serie con la línea. Cuando los extremos tienen una longitud λ _g /2, el filtro será un filtro de paso de banda . En este caso, el equivalente de elementos concentrados son circuitos resonantes LC en serie con la línea. ^[70]

Los filtros de absorción disipan la energía en frecuencias no deseadas internamente en forma de calor. Esto contrasta con un diseño de filtro convencional donde las frecuencias no deseadas se reflejan de vuelta desde el puerto de entrada del filtro. Dichos filtros se utilizan cuando no es deseable que se envíe energía de vuelta hacia la fuente. Este es el caso de los transmisores de alta potencia donde la energía de retorno puede ser lo suficientemente alta como para dañar el transmisor. Se puede utilizar un filtro de absorción para eliminar emisiones espurias del transmisor, como armónicos o bandas laterales espurias . Un diseño que se ha utilizado durante algún tiempo tiene ranuras cortadas en las paredes de la guía de ondas de alimentación a intervalos regulares. Este diseño se conoce como filtro de ondas con fugas . Cada ranura está conectada a una guía de ondas de calibre más pequeño que es demasiado pequeña para soportar la propagación de frecuencias en la banda deseada. Por lo tanto, esas frecuencias no se ven afectadas por el filtro. Sin embargo, las frecuencias más altas en la banda no deseada se propagan fácilmente a lo largo de las guías laterales que terminan con una carga adaptada donde se absorbe la energía. Estas cargas suelen ser una pieza en forma de cuña de material absorbente de microondas. ^[71] Otro diseño de filtro de absorción, más compacto, utiliza resonadores con un dieléctrico con pérdidas. ^[72]

Existen muchas aplicaciones de filtros cuyos objetivos de diseño son algo más que el rechazo o el paso de ciertas frecuencias. Con frecuencia, un dispositivo simple que está destinado a funcionar solo en una banda estrecha o en una sola frecuencia puntual no se parecerá mucho a un diseño de filtro. Sin embargo, un diseño de banda ancha para el mismo elemento requiere muchos más elementos y el diseño adquiere la naturaleza de un filtro. Entre las aplicaciones más comunes de este tipo en guías de ondas se encuentran las redes de adaptación de impedancia , los acopladores direccionales, los divisores de potencia, los combinadores de potencia y los diplexores . Otras aplicaciones posibles incluyen multiplexores , demultiplexores, amplificadores de resistencia negativa y redes de retardo de tiempo . ^[73]

Un método simple de adaptación de impedancia es la adaptación de stubs con un solo stub. Sin embargo, un solo stub solo producirá una adaptación perfecta en una frecuencia particular. Por lo tanto, esta técnica solo es adecuada para aplicaciones de banda estrecha. Para ampliar el ancho de banda se pueden utilizar múltiples stubs, y la estructura entonces toma la forma de un filtro stub. El diseño procede como si fuera un filtro, excepto que se optimiza un parámetro diferente. En un filtro de frecuencia, normalmente el parámetro optimizado es el rechazo de banda suprimida, la atenuación de banda de paso, la inclinación de la transición o algún compromiso entre estos. En una red de adaptación, el parámetro optimizado es la adaptación de impedancia. La función del dispositivo no requiere una restricción del ancho de banda, pero el diseñador se ve obligado a elegir un ancho de banda debido a la estructura del dispositivo. ^[74]

Los stubs no son el único formato de filtro que se puede utilizar. En principio, cualquier estructura de filtro se puede aplicar a la adaptación de impedancia, pero algunas darán como resultado diseños más prácticos que otras. Un formato frecuente utilizado para la adaptación de impedancia en guías de onda es el filtro de impedancia escalonada. Un ejemplo se puede ver en el duplexor ^[e] que se muestra en la figura 13. ^[75]

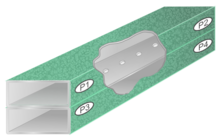
Los acopladores direccionales, los divisores de potencia y los combinadores de potencia son esencialmente el mismo tipo de dispositivo, al menos cuando se implementan con componentes pasivos . Un acoplador direccional divide una pequeña cantidad de potencia de la línea principal a un tercer puerto. Un dispositivo más fuertemente acoplado, pero idéntico en todo lo demás, puede llamarse divisor de potencia. El que acopla exactamente la mitad de la potencia al tercer puerto (un acoplador de 3 dB ) es el acoplamiento máximo que se puede lograr sin invertir las funciones de los puertos. Muchos diseños de divisores de potencia se pueden utilizar a la inversa, con lo que se convierten en combinadores de potencia. ^[76]

Una forma simple de acoplador direccional es la de dos líneas de transmisión paralelas acopladas entre sí en una longitud de λ/4. Este diseño es limitado porque la longitud eléctrica del acoplador solo será λ/4 en una frecuencia específica. El acoplamiento será máximo en esta frecuencia y disminuirá en ambos lados. De manera similar al caso de adaptación de impedancia, esto se puede mejorar utilizando múltiples elementos, lo que da como resultado una estructura similar a un filtro. ^[77] Un análogo de guía de ondas de este enfoque de líneas acopladas es el acoplador direccional de Bethe-hole en el que dos guías de ondas paralelas se apilan una sobre la otra y se proporciona un orificio para el acoplamiento. Para producir un diseño de banda ancha, se utilizan múltiples orificios a lo largo de las guías como se muestra en la figura 14 y se aplica un diseño de filtro. ^[78] No es solo el diseño de línea acoplada el que sufre por ser de banda estrecha, todos los diseños simples de acoplador de guía de ondas dependen de la frecuencia de alguna manera. Por ejemplo, el acoplador de carrera de ratas (que se puede implementar directamente en la guía de ondas) funciona con un principio completamente diferente, pero aún depende de que ciertas longitudes sean exactas en términos de λ. ^[79]

Un diplexor es un dispositivo que se utiliza para combinar dos señales que ocupan diferentes bandas de frecuencia en una sola señal. Esto suele ser para permitir que dos señales se transmitan simultáneamente en el mismo canal de comunicaciones, o para permitir transmitir en una frecuencia mientras se recibe en otra. (Este uso específico de un diplexor se denomina duplexor). El mismo dispositivo se puede utilizar para separar las señales de nuevo en el extremo más alejado del canal. La necesidad de filtrar para separar las señales mientras se recibe es bastante evidente, pero también es necesario incluso cuando se combinan dos señales transmitidas. Sin filtrado, parte de la potencia de la fuente A se enviará a la fuente B en lugar de a la salida combinada. Esto tendrá los efectos perjudiciales de perder una parte de la potencia de entrada y cargar la fuente A con la impedancia de salida de la fuente B, lo que provocará un desajuste. Estos problemas se podrían superar con el uso de un acoplador direccional de 3 dB , pero como se explicó en la sección anterior, un diseño de banda ancha también requiere un diseño de filtro para acopladores direccionales. ^[80]

Dos señales de banda estrecha muy espaciadas se pueden diplexar uniendo las salidas de dos filtros de paso de banda adecuados. Se deben tomar medidas para evitar que los filtros se acoplen entre sí cuando están en resonancia, lo que provocaría una degradación de su rendimiento. Esto se puede lograr con un espaciado adecuado. Por ejemplo, si los filtros son del tipo acoplado por iris, el iris más cercano a la unión del filtro A se coloca a λ _gb /4 de la unión, donde λ _gb es la longitud de onda de guía en la banda de paso del filtro B. Del mismo modo, el iris más cercano del filtro B se coloca a λ _ga /4 de la unión. Esto funciona porque cuando el filtro A está en resonancia, el filtro B está en su banda de rechazo y solo está acoplado de forma flexible y viceversa. Una disposición alternativa es tener cada filtro unido a una guía de ondas principal en uniones separadas. Se coloca un resonador de desacoplamiento a λ _g /4 de la unión de cada filtro. Esto puede ser en forma de un trozo cortocircuitado sintonizado a la frecuencia resonante de ese filtro. Esta disposición se puede extender a multiplexores con cualquier número de bandas. ^[81]

En el caso de los diplexores que trabajan con bandas de paso contiguas, es necesario tener en cuenta en el diseño las características de cruce de los filtros. Un caso especialmente común de esto es cuando el diplexor se utiliza para dividir todo el espectro en bandas bajas y altas. En este caso, se utilizan un filtro de paso bajo y un filtro de paso alto en lugar de filtros de paso de banda. Las técnicas de síntesis utilizadas aquí se pueden aplicar igualmente a multiplexores de banda estrecha y eliminan en gran medida la necesidad de resonadores de desacoplamiento. ^[82]

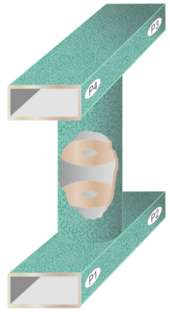
Un filtro direccional es un dispositivo que combina las funciones de un acoplador direccional y un diplexor. Como se basa en un acoplador direccional, es esencialmente un dispositivo de cuatro puertos, pero al igual que los acopladores direccionales, el puerto 4 suele estar permanentemente terminado internamente. La energía que entra al puerto 1 sale por el puerto 3 después de estar sujeta a alguna función de filtrado (normalmente paso de banda). La energía restante sale por el puerto 2 y, como no se absorbe ni se refleja energía, ésta será el complemento exacto de la función de filtrado en el puerto 2, en este caso, el filtro de banda. A la inversa, la energía que entra a los puertos 2 y 3 se combina en el puerto 1, pero ahora la energía de las señales rechazadas por el filtro se absorbe en la carga en el puerto 4. La Figura 15 muestra una posible implementación de guía de ondas de un filtro direccional. Dos guías de ondas rectangulares que funcionan en el modo TE ₁₀ dominante proporcionan los cuatro puertos. Estos están unidos entre sí por una guía de ondas circular que funciona en el modo TE ₁₁ circular . La guía de ondas circular contiene un filtro acoplado a iris con tantos iris como sean necesarios para producir la respuesta de filtro requerida. ^[83]

^ apertura

Una abertura en una pared de una guía de ondas o barrera entre secciones de una guía de ondas a través de la cual puede propagarse la radiación electromagnética.

^ ^ab impedancia característica

La impedancia característica , símbolo Z ₀ , de una guía de ondas para un modo particular se define como la relación entre el campo eléctrico transversal y el campo magnético transversal de una onda que viaja en una dirección a lo largo de la guía. La impedancia característica para una guía de ondas llena de aire se expresa mediante:

${\displaystyle Z_{0}=\left\{{\begin{matrix}Z_{\mathrm {f} }{\dfrac {\lambda _{\mathrm {g} }}{\lambda }}&{\text{(modo TE)}}\\\\Z_{\mathrm {f} }{\dfrac {\lambda }{\lambda _{\mathrm {g} }}}&{\text{(modo TM)}}\end{matrix}}\right.}$

donde Z _f es la impedancia del espacio libre , aproximadamente 377 Ω , λ _g es la longitud de onda de la guía y λ es la longitud de onda sin restricciones de la guía. Para una guía de ondas llena de dieléctrico, la expresión debe dividirse por √ κ , donde κ es la constante dieléctrica del material y λ se reemplaza por la longitud de onda sin restricciones en el medio dieléctrico. En algunos tratamientos, lo que aquí se denomina impedancia característica se denomina impedancia de onda, y la impedancia característica se define como proporcional a ella mediante alguna constante. ^[84]

^ ^cdediplexor ,duplexor

Un diplexor combina o separa dos señales que ocupan diferentes bandas de paso. Un duplexor combina o divide dos señales que viajan en direcciones opuestas o con polarizaciones diferentes (que también pueden estar en diferentes bandas de paso).

^ Plano E

El plano E es el plano que se encuentra en la dirección del campo eléctrico transversal, es decir, verticalmente a lo largo de la guía. ^[85]

^ longitud de onda guía

La longitud de onda de la guía, cuyo símbolo es λ _g , es la longitud de onda medida longitudinalmente a lo largo de la guía de ondas. Para una frecuencia dada, λ _g depende del modo de transmisión y siempre es mayor que la longitud de onda de una onda electromagnética de la misma frecuencia en el espacio libre. λ _g está relacionada con la frecuencia de corte, f _c , por:

${\displaystyle \lambda _{\mathrm {g} }={\frac {\lambda }{\sqrt {1-\left({\frac {f_{\mathrm {c} }}{f}}\right)^{2}}}}}$

donde λ es la longitud de onda que tendría la onda si no estuviera restringida por la guía. Para las guías que están llenas solo de aire, será la misma, para todos los efectos prácticos, que la longitud de onda en el espacio libre para la frecuencia transmitida, f . ^[86]

^ Plano H

El plano H es el plano que se encuentra en la dirección del campo magnético transversal ( H es el símbolo de análisis de la intensidad del campo magnético ), es decir, horizontalmente a lo largo de la guía. ^[85]

^ ^yoaltura ,ancho

En el caso de una guía rectangular, se refieren respectivamente a las pequeñas y grandes dimensiones internas de su sección transversal. La polarización del campo E del modo dominante es paralela a la altura.

^ iris

Una placa conductora colocada transversalmente a la guía de ondas con una apertura, normalmente grande.

^de terminación simple ,doblemente terminado

Un filtro de doble terminación (el caso normal) es aquel en el que el generador y la carga, conectados a los puertos de entrada y salida respectivamente, tienen impedancias que coinciden con la impedancia característica del filtro. Un filtro de terminación simple tiene una carga coincidente, pero es accionado por una fuente de voltaje de baja impedancia o una fuente de corriente de alta impedancia. ^[87]

^ Modo TEM

Modo electromagnético transversal, modo de transmisión en el que todo el campo eléctrico y todo el campo magnético son perpendiculares a la dirección de propagación de la onda electromagnética. Este es el modo de transmisión habitual en pares de conductores. ^[88]

^ Modo TE

Modo eléctrico transversal, uno de los muchos modos en los que todo el campo eléctrico, pero no todo el campo magnético, es perpendicular a la dirección de propagación de la onda electromagnética. En algunas fuentes se los designa como modos H porque tienen un componente magnético longitudinal. El primer índice indica el número de medias longitudes de onda del campo a lo ancho de la guía de ondas, y el segundo índice indica el número de medias longitudes de onda a lo alto. Lo correcto es que los índices se separen con una coma, pero normalmente se los utiliza juntos, ya que rara vez es necesario considerar los números de modo de dos cifras. A continuación se enumeran algunos modos mencionados específicamente en este artículo. Todos los modos son para guías de ondas rectangulares a menos que se indique lo contrario. ^[89]

^ Modo TE ₀₁

Un modo con media onda de campo eléctrico a lo largo de la altura de la guía y un campo eléctrico uniforme (cero medias ondas) a lo largo del ancho de la guía.

^ Modo TE ₁₀

Un modo con media onda de campo eléctrico a lo ancho de la guía y un campo eléctrico uniforme a lo largo de la altura de la guía.

^ Modo TE ₂₀

Un modo con dos medias ondas de campo eléctrico a lo ancho de la guía y un campo eléctrico uniforme a lo largo de la altura de la guía.

^ TE ₁₁ modo circular

Un modo con una onda completa de campo eléctrico alrededor de la circunferencia de la guía y media onda de campo eléctrico a lo largo de un radio.

^ Modo TM

Modo magnético transversal, uno de los muchos modos en los que todo el campo magnético, pero no todo el campo eléctrico, es perpendicular a la dirección de propagación de la onda electromagnética. En algunas fuentes se los denomina modos E porque tienen un componente eléctrico longitudinal. Consulte el modo TE para obtener una descripción del significado de los índices. Algunos modos mencionados específicamente en este artículo son:

^ Modo TM ₁₁

Un modo con media onda de campo magnético a lo ancho de la guía y media onda de campo magnético a lo alto de la guía. Este es el modo TM más bajo, ya que no pueden existir modos TM _{m 0.} ^[90]

^ TM ₀₁ modo circular

Un modo con campo magnético uniforme alrededor de la circunferencia de la guía y media onda de campo magnético a lo largo de un radio.

^ línea de transmisión ^op

Una línea de transmisión es un medio de transmisión de señales que consiste en un par de conductores eléctricos separados entre sí, o un conductor y una vía de retorno común. En algunos estudios, las guías de ondas se consideran dentro de la clase de líneas de transmisión, con las que tienen mucho en común. En este artículo, las guías de ondas no se incluyen para que los dos tipos de medios se puedan distinguir y referenciar más fácilmente.

• Bagad, VS, Ingeniería de microondas , Publicaciones técnicas Pune, 2009 ISBN  81-8431-360-8 .
• Belov, Leonid A.; Smolskiy, Sergey M.; Kochemasov, Victor N., Manual de componentes de RF, microondas y ondas milimétricas , Artech House, 2012 ISBN 1-60807-209-6 . 
• Bowen, Edward George, Un libro de texto sobre radar , Cambridge University Press, 1954 OCLC  216292853.
• Bray, John, Innovación y la revolución de las comunicaciones: desde los pioneros victorianos hasta Internet de banda ancha , IEE, 2002 ISBN 0-85296-218-5 . 
• Cauer, E.; Mathis W.; Pauli, R., "Vida y obra de Wilhelm Cauer (1900 – 1945)", Actas del Decimocuarto Simposio Internacional de Teoría Matemática de Redes y Sistemas (MTNS2000) , Perpignan, junio de 2000 OCLC  65290907.
• Connor, FR, Transmisión de ondas , Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7 . 
• Cohn, SB, "Filtros de microondas que contienen resonadores dieléctricos de alto Q", G-MTT Symposium Digest, páginas 49-50, 5-7 de mayo de 1965.
• Cristal, Edward G., "Solución analítica para una estructura de filtro de ondas con fugas de guía de ondas", IEEE Transactions on Microwave Theory and Techniques , volumen 11, número 3, páginas 182–190, 1963.
• Cristal, Edward G.; Matthaei, GL, "Una técnica para el diseño de multiplexores con canales contiguos", IEEE Transactions on Microwave Theory and Techniques , volumen 12, número 1, páginas 88–93, 1964.
• Das, Annapurna; Das, Sisir K, Ingeniería de microondas , Tata McGraw-Hill Education, 2009 ISBN 0-07-066738-1 . 
• Elmore, William Cronk; Heald, Mark Aiken, Física de ondas , Courier Dover Publications, 1969 ISBN 0-486-14065-2 . 
• Eskelinen, Harri; Eskelinen, Pekka, Mecánica de componentes de microondas , Artech House, 2003 ISBN 1-58053-589-5 . 
• Fano, RM; Lawson, AW, "Diseño de filtros de microondas", capítulo 10 de Ragan, GL (ed.), Microwave Transmission Circuits , McGraw-Hill, 1948 OCLC  2205252.
• Gibilisco, Stan; Sclater, Neil, Enciclopedia de electrónica , Tab Professional and Reference Books, 1990 ISBN 0-8306-3389-8 . 
• Golio, Mike, Manual de componentes y circuitos inalámbricos comerciales , CRC Press, 2002 ISBN 1-4200-3996-2 . 
• Griffin, EL; Young, FA, "Una comparación de cuatro filtros de paso de banda estrechos canónicos sobremodificados a 12 GHz", Microwave Symposium Digest, 1978 IEEE-MTT-S International , páginas 47–49.
• Gusmano, G.; Bianco, A.; Viticoli, M.; Kaciulis, S.; Mattogno, G.; Pandolfi, L., "Estudio de películas delgadas de Zr1−xSnxTiO4 preparadas mediante una ruta de precursor polimérico", Surface and Interface Analysis , volumen 34, número 1, páginas 690–693, agosto de 2002.
• Hitchcock, R. Timothy; Patterson, Robert M., Energías electromagnéticas de radiofrecuencia y ELF: un manual para profesionales de la salud , John Wiley & Sons, 1995 ISBN 0-471-28454-8 . 
• Hunter, IC, Teoría y diseño de filtros de microondas , IET, 2001 ISBN 0-85296-777-2 . 
• Huurdeman, Anton A., La historia mundial de las telecomunicaciones , Wiley-IEEE, 2003 ISBN 0-471-20505-2 . 
• Ishii, Thomas Koryu, Manual de tecnología de microondas: componentes y dispositivos , Academic Press, 1995 ISBN 0-12-374696-5 . 
• Jarry, Pierre; Beneat, Jacques, Diseño y realizaciones de filtros fractales miniaturizados de microondas y RF , John Wiley & Sons, 2009 ISBN 0-470-48781-X . 
• Ke, Wu; Lei, Zhu; Vahldieck, Ruediger, "Componentes pasivos de microondas", en Chen, Wai-Kei (ed.), The Electrical Engineering Handbook , Academic Press, 2004 ISBN 0-08-047748-8 . 
• Lee, Thomas H., Ingeniería de microondas planar , páginas 585–618, Cambridge University Press, 2004 ISBN 0-521-83526-7 . 
• Levy, R.; Cohn, SB, "Una historia de la investigación, el diseño y el desarrollo de filtros de microondas", IEEE Transactions: Microwave Theory and Techniques , páginas 1055–1067, volumen 32, número 9, 1984.
• Mahmoud, SF, Guías de ondas electromagnéticas: teoría y aplicaciones , IEE, 1991 ISBN 0-86341-232-7 . 
• Maloratsky, Leo G., Front-ends de microondas integrados con aplicaciones de aviónica , Artech House, 2012 ISBN 1-60807-206-1 . 
• Mansour, RR, "Filtros criogénicos tridimensionales" en H. Weinstock, H.; Nisenoff, M., Microwave Superconductivity , páginas 161–188, Springer, 2001 ISBN 1-4020-0445-1 . 
• Mason, WP; Sykes, RA "El uso de líneas de transmisión coaxiales y balanceadas en filtros y transformadores de banda ancha para altas frecuencias de radio", Bell System Technical Journal , páginas 275–302, volumen 16, 1937.
• Massé, DJ; Pucel, RA, "Un filtro de paso de banda estable a la temperatura utilizando resonadores dieléctricos", Actas del IEEE , volumen 60, número 6, páginas 730–731, junio de 1972.
• Matthaei, George L.; Young, Leo; Jones, EMT, Filtros de microondas, redes de adaptación de impedancia y estructuras de acoplamiento , McGraw-Hill, 1964 LCCN  64-7937.
• Meier, Paul J., "Dos nuevos medios de circuitos integrados con ventajas especiales en longitudes de onda milimétricas", Simposio Internacional de Microondas IEEE GMTT de 1972 , páginas 221–223, 22–24 de mayo de 1972.
• Meredith, Roger, Manual de ingenieros de calentamiento industrial por microondas , IET, 1998 ISBN 0-85296-916-3 . 
• Middleton, Wendy M.; Van Valkenburg, Mac Elwyn, Datos de referencia para ingenieros: radio, electrónica, computadoras y comunicaciones , Newnes, 2002 ISBN 0-7506-7291-9 . 
• Millman, S. (ed.), Una historia de ingeniería y ciencia en el sistema Bell: Ciencias de la comunicación (1925–1980) , AT&T Bell Laboratories, 1984 ISBN 0-932764-06-1 . 
• Minakova, LB; Rud, LA, "Enfoque de frecuencia natural para la síntesis de filtros de absorción de guía de ondas de banda estrecha", 32a Conferencia Europea de Microondas, 2002 , 23-26 de septiembre de 2002, Milán.
• Montgomery, Carol Gray; Dicke, Robert Henry; Purcell, Edward M., Principios de circuitos de microondas , IEE, 1948 ISBN 0-86341-100-2 . 
• Nalwa, Hari Singh (ed), Manual de materiales de constante dieléctrica baja y alta y sus aplicaciones , Academic Press, 1999 ISBN 0-08-053353-1 . 
• Pierce, JR, "Filtros de resonador paralelo", Actas del IRE, volumen 37, páginas 152-155, febrero de 1949.
• Radmanesh, Matthew M., Diseño avanzado de circuitos de RF y microondas , AuthorHouse, 2009 ISBN 1-4259-7244-6 . 
• Rhodes, JD, "Diseño directo de diplexores de canal de paso de banda interactuantes simétricos", IEE Journal on Microwaves, Optics and Acoustics , volumen 1, número 1, páginas 34–40, septiembre de 1976.
• Rhodes, JD; Levy, R., "Una teoría de multiplexores generalizada", IEEE Transactions on Microwave Theory and Techniques , volumen 27, número 2, páginas 99–111, febrero de 1979.
• Richards, Paul I., "Circuitos de líneas de transmisión por resistencias", Actas del IRE , volumen 36, páginas 217–220, febrero de 1948.
• Russer, Peter, Electromagnetismo, circuitos de microondas y diseño de antenas para ingeniería de comunicaciones , Artech House, 2003 ISBN 1-58053-532-1 . 
• Sarkar, TK ; Mailloux, Robert; Oliner, Arthur A. ; Salazar-Palma, M.; Sengupta Dipak L., Historia de la tecnología inalámbrica , John Wiley & Sons, 2006 ISBN 0-471-78301-3 . 
• Schumacher, HL, "Multiplexores coaxiales: clave para la clasificación de señales EW", Microwave Systems News , páginas 89-93, agosto/septiembre de 1976 ISSN  0164-3371
• Silver, Samuel, Teoría y diseño de antenas de microondas , IEE, 1949 ISBN 0-86341-017-0 . 
• Sorrentino, Roberto; Bianchi, Giovanni, Ingeniería de microondas y RF , John Wiley & Sons, 2010 ISBN 0-470-66021-X . 
• Srivastava, Ganesh Prasad; Gupta, Vijay Laxmi, Dispositivos de microondas y diseños de circuitos , Prentice-Hall de India, 2006 ISBN 81-203-2195-2 . 
• Waterhouse, Rod, Antenas de parche de microbanda: una guía para diseñadores , Springer, 2003 ISBN 1-4020-7373-9 . 
• Wenzel, JR, "Aplicación de métodos de síntesis exactos al diseño de filtros multicanal", IEEE Transactions on Microwave Theory and Techniques , volumen 13, número 1, páginas 5-15, enero de 1965.
• Xuan, Hu Wu; Kishk, Ahmed A., Análisis y diseño de guía de ondas integrada en sustrato utilizando un método híbrido 2D eficiente , Morgan & Claypool, 2010 ISBN 1-59829-902-6 . 
• Yeh, C.; Shimabukuro, FI, La esencia de las guías de ondas dieléctricas , Springer, 2008 ISBN 0-387-49799-4 . 
• Young, L., "Filtros de cavidad acoplados directamente para anchos de banda amplios y estrechos", IEEE Transactions: Microwave Theory and Techniques , volumen MTT-11, páginas 162–178, mayo de 1963.
• Young, Soo Lee; Getsinger, WJ; Sparrow, LR, "Tecnología MIC de tetratitanato de bario", IEEE Transactions on Microwave Theory and Techniques , volumen 27, número 7, páginas 655–660, julio de 1979.
• Zhang, Xianrong; Wang, Qingyuan; Li, Hong; Liu, Rongjun, "Filtro de guía de onda compacto de modo evanescente", Conferencia internacional sobre tecnología de microondas y ondas milimétricas, 2008 (ICMMT 2008) , volumen 1, páginas 323–325, IEEE, 2008.