Modelo de elementos concentrados

Este artículo puede resultar demasiado técnico para que la mayoría de los lectores lo entiendan . Ayúdenos a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Agosto de 2019 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Modelo de elementos concentrados» – noticias  · periódicos  · libros  · académico  · JSTOR ( agosto de 2023 ) ( Aprenda cómo y cuándo eliminar este mensaje )

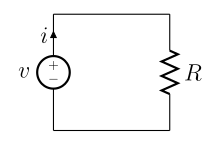
El modelo de elementos concentrados (también llamado modelo de parámetros concentrados o modelo de componentes concentrados ) es una representación simplificada de un sistema físico o circuito que supone que todos los componentes están concentrados en un único punto y su comportamiento puede describirse mediante modelos matemáticos idealizados. El modelo de elementos concentrados simplifica la descripción del comportamiento del sistema o circuito en una topología . Es útil en sistemas eléctricos (incluida la electrónica ), sistemas mecánicos multicuerpo , transferencia de calor , acústica , etc. Esto contrasta con los sistemas o modelos de parámetros distribuidos en los que el comportamiento se distribuye espacialmente y no puede considerarse localizado en entidades discretas.

La simplificación reduce el espacio de estados del sistema a una dimensión finita y las ecuaciones diferenciales parciales (EDP) del modelo de tiempo y espacio continuo (de dimensión infinita) del sistema físico en ecuaciones diferenciales ordinarias (EDO) con un número finito de parámetros.

La disciplina de materia concentrada es un conjunto de suposiciones impuestas en ingeniería eléctrica que proporciona la base para la abstracción de circuitos concentrados utilizada en el análisis de redes . ^[1] Las restricciones autoimpuestas son:

1. El cambio del flujo magnético en el tiempo fuera de un conductor es cero.$${\displaystyle {\frac {\partial \phi _{B}}{\partial t}}=0}$$
2. El cambio de la carga en el tiempo dentro de los elementos conductores es cero.$${\displaystyle {\frac {\parcial q}{\parcial t}}=0}$$
3. Las escalas de tiempo de las señales de interés son mucho mayores que el retardo de propagación de las ondas electromagnéticas a través del elemento concentrado.

Las dos primeras suposiciones dan como resultado las leyes de circuitos de Kirchhoff cuando se aplican a las ecuaciones de Maxwell y solo son aplicables cuando el circuito está en estado estable . La tercera suposición es la base del modelo de elementos concentrados que se utiliza en el análisis de redes . Suposiciones menos severas dan como resultado el modelo de elementos distribuidos , aunque aún no requieren la aplicación directa de las ecuaciones de Maxwell completas.

El modelo de elementos concentrados de los circuitos electrónicos parte del supuesto simplificador de que los atributos del circuito ( resistencia , capacitancia , inductancia y ganancia ) se concentran en componentes eléctricos idealizados ( resistencias , capacitores e inductores , etc.) unidos por una red de cables perfectamente conductores .

El modelo de elementos concentrados es válido siempre que , donde denota la longitud característica del circuito y denota la longitud de onda de funcionamiento del circuito . De lo contrario, cuando la longitud del circuito es del orden de una longitud de onda, debemos considerar modelos más generales, como el modelo de elementos distribuidos (incluidas las líneas de transmisión ), cuyo comportamiento dinámico se describe mediante las ecuaciones de Maxwell . Otra forma de ver la validez del modelo de elementos concentrados es observar que este modelo ignora el tiempo finito que tardan las señales en propagarse alrededor de un circuito. Siempre que este tiempo de propagación no sea significativo para la aplicación, se puede utilizar el modelo de elementos concentrados. Este es el caso cuando el tiempo de propagación es mucho menor que el período de la señal involucrada. Sin embargo, al aumentar el tiempo de propagación habrá un error creciente entre la fase supuesta y la real de la señal, lo que a su vez da como resultado un error en la amplitud supuesta de la señal. El punto exacto en el que ya no se puede utilizar el modelo de elementos concentrados depende en cierta medida de la precisión con la que se necesita conocer la señal en una aplicación determinada.${\displaystyle L_{c}\ll \lambda}$$Estilo de visualización L_{c}}$${\estilo de visualización \lambda}$

Los componentes del mundo real presentan características no ideales que, en realidad, son elementos distribuidos, pero que a menudo se representan con una aproximación de primer orden mediante elementos concentrados. Para tener en cuenta la fuga en los condensadores , por ejemplo, podemos modelar el condensador no ideal como si tuviera una gran resistencia concentrada conectada en paralelo, aunque la fuga, en realidad, está distribuida por todo el dieléctrico. De manera similar, una resistencia de alambre bobinado tiene una inductancia significativa , así como una resistencia distribuida a lo largo de su longitud, pero podemos modelarla como un inductor concentrado en serie con la resistencia ideal.

Un modelo de capacitancia concentrada , también llamado análisis de sistemas concentrados , ^[2] reduce un sistema térmico a una serie de “concentraciones” discretas y supone que la diferencia de temperatura dentro de cada una de ellas es insignificante. Esta aproximación es útil para simplificar ecuaciones diferenciales de calor que de otro modo serían complejas . Se desarrolló como un análogo matemático de la capacitancia eléctrica , aunque también incluye análogos térmicos de la resistencia eléctrica .

El modelo de capacitancia concentrada es una aproximación común en la conducción transitoria, que puede utilizarse siempre que la conducción de calor dentro de un objeto sea mucho más rápida que la transferencia de calor a través de los límites del objeto. El método de aproximación reduce entonces adecuadamente un aspecto del sistema de conducción transitoria (la variación de temperatura espacial dentro del objeto) a una forma matemáticamente más manejable (es decir, se supone que la temperatura dentro del objeto es completamente uniforme en el espacio, aunque este valor de temperatura uniforme espacialmente cambia con el tiempo). La temperatura uniforme creciente dentro del objeto o parte de un sistema puede entonces tratarse como un depósito capacitivo que absorbe calor hasta que alcanza un estado térmico estable en el tiempo (después de lo cual la temperatura no cambia dentro de él).

Un ejemplo temprano de un sistema de capacitancia concentrada que exhibe un comportamiento matemáticamente simple debido a tales simplificaciones físicas, son los sistemas que se ajustan a la ley de enfriamiento de Newton . Esta ley simplemente establece que la temperatura de un objeto caliente (o frío) progresa hacia la temperatura de su entorno de una manera exponencial simple. Los objetos siguen esta ley estrictamente solo si la tasa de conducción de calor dentro de ellos es mucho mayor que el flujo de calor dentro o fuera de ellos. En tales casos tiene sentido hablar de una única "temperatura del objeto" en un momento dado (ya que no hay variación de temperatura espacial dentro del objeto) y también las temperaturas uniformes dentro del objeto permiten que su exceso o déficit de energía térmica total varíe proporcionalmente a su temperatura superficial, estableciendo así el requisito de la ley de enfriamiento de Newton de que la tasa de disminución de la temperatura es proporcional a la diferencia entre el objeto y el entorno. Esto a su vez conduce a un comportamiento de calentamiento o enfriamiento exponencial simple (detalles a continuación).

Para determinar el número de grumos, se utiliza el número de Biot (Bi), un parámetro adimensional del sistema. Bi se define como la relación entre la resistencia al calor conductivo dentro del objeto y la resistencia a la transferencia de calor por convección a través del límite del objeto con un baño uniforme de diferente temperatura. Cuando la resistencia térmica al calor transferido al objeto es mayor que la resistencia a que el calor se difunda completamente dentro del objeto, el número de Biot es menor que 1. En este caso, particularmente para números de Biot que son incluso menores, se puede empezar a utilizar la aproximación de la temperatura uniforme espacialmente dentro del objeto , ya que se puede presumir que el calor transferido al objeto tiene tiempo de distribuirse uniformemente, debido a la menor resistencia a hacerlo, en comparación con la resistencia al calor que entra en el objeto.

Si el número de Biot es menor que 0,1 para un objeto sólido, entonces todo el material tendrá casi la misma temperatura, con la diferencia de temperatura dominante en la superficie. Puede considerarse como "térmicamente delgado". El número de Biot debe ser generalmente menor que 0,1 para una aproximación útil y precisa y para un análisis de transferencia de calor. La solución matemática para la aproximación del sistema concentrado da la ley de enfriamiento de Newton .

Un número de Biot mayor que 0,1 (una sustancia "térmicamente espesa") indica que no se puede hacer esta suposición y se requerirán ecuaciones de transferencia de calor más complicadas para la "conducción de calor transitoria" para describir el campo de temperatura variable en el tiempo y no uniforme espacialmente dentro del cuerpo material.

El enfoque de capacitancia única se puede ampliar para incluir muchos elementos resistivos y capacitivos, con Bi < 0,1 para cada bloque. Como el número de Biot se calcula en función de una longitud característica del sistema, el sistema a menudo se puede dividir en una cantidad suficiente de secciones o bloques, de modo que el número de Biot sea aceptablemente pequeño.

Algunas longitudes características de los sistemas térmicos son:

• Placa: espesor
• Aleta : espesor/2
• Cilindro largo : diámetro/4
• Esfera : diámetro/6

Para formas arbitrarias, puede ser útil considerar que la longitud característica es el volumen/área de superficie.

Un concepto útil que se utiliza en aplicaciones de transferencia de calor una vez que se ha alcanzado la condición de conducción de calor en estado estable es la representación de la transferencia térmica mediante lo que se conoce como circuitos térmicos. Un circuito térmico es la representación de la resistencia al flujo de calor en cada elemento de un circuito, como si fuera una resistencia eléctrica . El calor transferido es análogo a la corriente eléctrica y la resistencia térmica es análoga a la resistencia eléctrica. Los valores de la resistencia térmica para los diferentes modos de transferencia de calor se calculan entonces como los denominadores de las ecuaciones desarrolladas. Las resistencias térmicas de los diferentes modos de transferencia de calor se utilizan para analizar modos combinados de transferencia de calor. La falta de elementos "capacitativos" en el siguiente ejemplo puramente resistivo significa que ninguna sección del circuito está absorbiendo energía o cambiando la distribución de la temperatura. Esto es equivalente a exigir que ya se haya establecido un estado de conducción de calor en estado estable (o transferencia, como en la radiación).

Las ecuaciones que describen los tres modos de transferencia de calor y sus resistencias térmicas en condiciones de estado estable, como se discutió anteriormente, se resumen en la siguiente tabla:

Ecuaciones para diferentes modos de transferencia de calor y sus resistencias térmicas.

Modo de transferencia	Tasa de transferencia de calor	Resistencia térmica
Conducción	${\displaystyle {\dot {Q}}={\frac {T_{1}-T_{2}}{\left({\frac {L}{kA}}\right)}}}$	${\displaystyle {\frac {L}{kA}}}$
Convección	${\displaystyle {\dot {Q}}={\frac {T_{\rm {surf}}-T_{\rm {envr}}}{\left({\frac {1}{h_{\rm {conv}}A_{\rm {surf}}}}\right)}}}$	${\displaystyle {\frac {1}{h_{\rm {conv}}A_{\rm {surf}}}}}$
Radiación	${\displaystyle {\dot {Q}}={\frac {T_{\rm {surf}}-T_{\rm {surr}}}{\left({\frac {1}{h_{r}A_{\rm {surf}}}}\right)}}}$	${\displaystyle {\frac {1}{h_{r}A}}}$, dónde ${\displaystyle h_{r}=\epsilon \sigma (T_{\rm {surf}}^{2}+T_{\rm {surr}}^{2})(T_{\rm {surf}}+T_{\rm {surr}})}$

En los casos en los que existe transferencia de calor a través de diferentes medios (por ejemplo, a través de un material compuesto ), la resistencia equivalente es la suma de las resistencias de los componentes que forman el compuesto. Probablemente, en los casos en los que existen diferentes modos de transferencia de calor, la resistencia total es la suma de las resistencias de los diferentes modos. Utilizando el concepto de circuito térmico, la cantidad de calor transferida a través de cualquier medio es el cociente del cambio de temperatura y la resistencia térmica total del medio.

Como ejemplo, considere una pared compuesta con un área de sección transversal de . La pared compuesta está hecha de un yeso de cemento largo con un coeficiente térmico y una fibra de vidrio revestida con papel largo, con un coeficiente térmico de . La superficie izquierda de la pared está a y expuesta al aire con un coeficiente de convección de . La superficie derecha de la pared está a y expuesta al aire con un coeficiente de convección de .${\estilo de visualización A}$$Estilo de visualización L_{1}$$estilo de visualización k_{1}$$Estilo de visualización L_{2}$$estilo de visualización k_{2}$$Estilo de visualización T_{i}}$$estilo de visualización h_{i}}$${\displaystyle T_{o}}$${\displaystyle h_{o}}$

Utilizando el concepto de resistencia térmica, el flujo de calor a través del compuesto es el siguiente: donde , , , y$${\displaystyle {\dot {Q}}={\frac {T_{i}-T_{o}}{R_{i}+R_{1}+R_{2}+R_{o}}}={\frac {T_{i}-T_{1}}{R_{i}}}={\frac {T_{i}-T_{2}}{R_{i}+R_{1}}}={\frac {T_{i}-T_{3}}{R_{i}+R_{1}+R_{2}}}={\frac {T_{1}-T_{2}}{R_{1}}}={\frac {T_{3}-T_{o}}{R_{0}}}}$$${\displaystyle R_{i}={\frac {1}{h_{i}A}}}$${\displaystyle R_{o}={\frac {1}{h_{o}A}}}$${\displaystyle R_{1}={\frac {L_{1}}{k_{1}A}}}$${\displaystyle R_{2}={\frac {L_{2}}{k_{2}A}}}$

La ley de enfriamiento de Newton es una relación empírica atribuida al físico inglés Sir Isaac Newton (1642-1727). Esta ley, expresada en forma no matemática, es la siguiente:

La tasa de pérdida de calor de un cuerpo es proporcional a la diferencia de temperatura entre el cuerpo y su entorno.

O bien, utilizando símbolos:$${\displaystyle {\text{Rate of cooling}}\sim \Delta T}$$

Un objeto que se encuentra a una temperatura diferente de la de su entorno acabará alcanzando una temperatura común con su entorno. Un objeto relativamente caliente se enfría al calentar su entorno; un objeto frío se calienta gracias a su entorno. Cuando consideramos la rapidez (o lentitud) con la que algo se enfría, hablamos de su velocidad de enfriamiento: cuántos grados cambia su temperatura por unidad de tiempo.

La velocidad de enfriamiento de un objeto depende de cuánto más caliente esté el objeto que su entorno. El cambio de temperatura por minuto de una tarta de manzana caliente será mayor si la tarta se coloca en un congelador frío que si se coloca en la mesa de la cocina. Cuando la tarta se enfría en el congelador, la diferencia de temperatura entre ella y su entorno es mayor. En un día frío, una casa cálida perderá calor al exterior a un ritmo mayor cuando haya una gran diferencia entre las temperaturas interior y exterior. Por lo tanto, mantener el interior de una casa a una temperatura alta en un día frío es más costoso que mantenerlo a una temperatura más baja. Si la diferencia de temperatura se mantiene pequeña, la velocidad de enfriamiento será correspondientemente baja.

Como establece la ley de enfriamiento de Newton, la velocidad de enfriamiento de un objeto (ya sea por conducción , convección o radiación ) es aproximadamente proporcional a la diferencia de temperatura Δ T. Los alimentos congelados se calentarán más rápido en una habitación cálida que en una habitación fría. Tenga en cuenta que la velocidad de enfriamiento experimentada en un día frío puede aumentar por el efecto de convección adicional del viento . Esto se conoce como sensación térmica . Por ejemplo, una sensación térmica de -20 °C significa que el calor se pierde a la misma velocidad que si la temperatura fuera de -20 °C sin viento.

Esta ley describe muchas situaciones en las que un objeto tiene una gran capacidad térmica y una gran conductividad y de repente se sumerge en un baño uniforme que conduce el calor relativamente mal. Es un ejemplo de un circuito térmico con un elemento resistivo y uno capacitivo. Para que la ley sea correcta, las temperaturas en todos los puntos dentro del cuerpo deben ser aproximadamente las mismas en cada momento, incluida la temperatura en su superficie. Por lo tanto, la diferencia de temperatura entre el cuerpo y el entorno no depende de qué parte del cuerpo se elija, ya que todas las partes del cuerpo tienen efectivamente la misma temperatura. En estas situaciones, el material del cuerpo no actúa para "aislar" otras partes del cuerpo del flujo de calor, y todo el aislamiento significativo (o "resistencia térmica") que controla la velocidad del flujo de calor en la situación reside en el área de contacto entre el cuerpo y su entorno. A través de este límite, el valor de la temperatura salta de manera discontinua.

En tales situaciones, el calor puede transferirse desde el exterior al interior de un cuerpo, a través de la frontera aislante, por convección, conducción o difusión, siempre que la frontera sirva como un conductor relativamente malo con respecto al interior del objeto. No se requiere la presencia de un aislante físico, siempre que el proceso que sirve para pasar el calor a través de la frontera sea "lento" en comparación con la transferencia conductiva de calor dentro del cuerpo (o dentro de la región de interés, el "bulto" descrito anteriormente).

En tal situación, el objeto actúa como el elemento del circuito "capacitativo" y la resistencia del contacto térmico en el límite actúa como la resistencia térmica (única). En los circuitos eléctricos, una combinación de este tipo se cargaría o descargaría hacia la tensión de entrada, según una ley exponencial simple en el tiempo. En el circuito térmico, esta configuración da como resultado el mismo comportamiento en temperatura: una aproximación exponencial de la temperatura del objeto a la temperatura del baño.

La ley de Newton se enuncia matemáticamente mediante la simple ecuación diferencial de primer orden: donde$${\displaystyle {\frac {dQ}{dt}}=-h\cdot A(T(t)-T_{\text{env}})=-h\cdot A\Delta T(t)}$$

• Q es energía térmica en julios
• h es el coeficiente de transferencia de calor entre la superficie y el fluido
• A es la superficie del calor que se transfiere
• T es la temperatura de la superficie y del interior del objeto (ya que son las mismas en esta aproximación)
• T _env es la temperatura del ambiente
• Δ T ( t ) = T ( t ) − T _{env es el} gradiente térmico dependiente del tiempo entre el entorno y el objeto

En ocasiones, expresar las transferencias de calor de esta forma no es una buena aproximación, ya que depende de las relaciones de conductancia térmica en el sistema. Si las diferencias no son grandes, una formulación precisa de las transferencias de calor en el sistema puede requerir un análisis del flujo de calor basado en la ecuación de transferencia de calor (transitoria) en medios no homogéneos o poco conductores.

Si se considera el cuerpo entero como un depósito de calor de capacitancia concentrada, con un contenido de calor total que es proporcional a la capacidad calorífica total simple , y , la temperatura del cuerpo, o . Se espera que el sistema experimente una disminución exponencial con el tiempo en la temperatura de un cuerpo.${\displaystyle C}$${\displaystyle T}$${\displaystyle Q=CT}$

De la definición de capacidad térmica se obtiene la relación . Al derivar esta ecuación con respecto al tiempo se obtiene la identidad (válida siempre que las temperaturas en el objeto sean uniformes en cualquier momento dado): . Esta expresión se puede utilizar para reemplazar en la primera ecuación que inicia esta sección, arriba. Entonces, si es la temperatura de dicho cuerpo en el momento , y es la temperatura del entorno que rodea al cuerpo: donde es una constante positiva característica del sistema, que debe estar en unidades de , y por lo tanto a veces se expresa en términos de una constante de tiempo característica dada por: . Por lo tanto, en sistemas térmicos, . (La capacidad térmica total de un sistema se puede representar además por su capacidad térmica específica de masa multiplicada por su masa , de modo que la constante de tiempo también está dada por ).${\displaystyle C}$${\displaystyle C=dQ/dT}$${\displaystyle dQ/dt=C(dT/dt)}$${\displaystyle dQ/dt}$${\displaystyle T(t)}$${\displaystyle t}$${\displaystyle T_{\text{env}}}$$${\displaystyle {\frac {dT(t)}{dt}}=-r(T(t)-T_{\text{env}})=-r\Delta T(t)}$$${\displaystyle r=hA/C}$${\displaystyle s^{-1}}$ ${\displaystyle t_{0}}$${\displaystyle t_{0}=1/r=-\Delta T(t)/(dT(t)/dt)}$${\displaystyle t_{0}=C/hA}$ ${\displaystyle C}$ ${\displaystyle c_{p}}$${\displaystyle m}$${\displaystyle t_{0}}$${\displaystyle mc_{p}/hA}$

La solución de esta ecuación diferencial, por métodos estándar de integración y sustitución de condiciones de contorno, da:$${\displaystyle T(t)=T_{\mathrm {env} }+(T(0)-T_{\mathrm {env} })\ e^{-rt}.}$$

Si:

${\displaystyle \Delta T(t)\quad }$se define como: donde es la diferencia de temperatura inicial en el tiempo 0,${\displaystyle T(t)-T_{\mathrm {env} }\ ,\quad }$${\displaystyle \Delta T(0)\quad }$

Entonces la solución newtoniana se escribe como:$${\displaystyle \Delta T(t)=\Delta T(0)\ e^{-rt}=\Delta T(0)\ e^{-t/t_{0}}.}$$

Esta misma solución es casi inmediatamente aparente si la ecuación diferencial inicial se escribe en términos de , como la única función a resolver.${\displaystyle \Delta T(t)}$$${\displaystyle {\frac {dT(t)}{dt}}={\frac {d\Delta T(t)}{dt}}=-{\frac {1}{t_{0}}}\Delta T(t)}$$

Este modo de análisis se ha aplicado a las ciencias forenses para analizar el momento de la muerte de seres humanos. También se puede aplicar a los sistemas de calefacción, ventilación y aire acondicionado ( HVAC , por sus siglas en inglés, a los que se puede denominar "control del clima de los edificios"), para garantizar efectos casi instantáneos de un cambio en el nivel de confort. ^[3]

Los supuestos simplificadores en este dominio son:

• todos los objetos son cuerpos rígidos ;
• Todas las interacciones entre cuerpos rígidos tienen lugar a través de pares cinemáticos ( articulaciones ), resortes y amortiguadores .

En este contexto, el modelo de componentes concentrados extiende los conceptos distribuidos de la teoría acústica sujetos a aproximación. En el modelo acústico de componentes concentrados, ciertos componentes físicos con propiedades acústicas pueden aproximarse como si se comportaran de manera similar a los componentes electrónicos estándar o a combinaciones simples de componentes.

• Una cavidad de paredes rígidas que contiene aire (o un fluido compresible similar) puede considerarse como un capacitor cuyo valor es proporcional al volumen de la cavidad. La validez de esta aproximación se basa en que la longitud de onda más corta de interés sea significativamente (mucho) mayor que la dimensión más larga de la cavidad.
• Un puerto réflex puede considerarse como un inductor cuyo valor es proporcional a la longitud efectiva del puerto dividida por su área de sección transversal. La longitud efectiva es la longitud real más una corrección final . Esta aproximación se basa en que la longitud de onda de interés más corta sea significativamente mayor que la dimensión más larga del puerto.
• Ciertos tipos de materiales amortiguadores pueden considerarse como una resistencia . El valor depende de las propiedades y dimensiones del material. La aproximación se basa en que las longitudes de onda sean lo suficientemente largas y en las propiedades del propio material.
• Una unidad de control de altavoz (normalmente una unidad de control de woofer o subwoofer ) puede representarse como una conexión en serie de una fuente de voltaje de impedancia cero , una resistencia , un capacitor y un inductor . Los valores dependen de las especificaciones de la unidad y de la longitud de onda de interés.

Una suposición simplificadora en este dominio es que todos los mecanismos de transferencia de calor son lineales, lo que implica que la radiación y la convección están linealizadas para cada problema.

Se pueden encontrar varias publicaciones que describen cómo generar modelos de elementos agrupados de edificios. En la mayoría de los casos, el edificio se considera una única zona térmica y, en este caso, convertir paredes de múltiples capas en elementos agrupados puede ser una de las tareas más complicadas en la creación del modelo. El método de la capa dominante es un método simple y razonablemente preciso. ^[4] En este método, una de las capas se selecciona como la capa dominante en toda la construcción, esta capa se elige considerando las frecuencias más relevantes del problema. ^[5]

Los modelos de elementos agrupados de edificios también se han utilizado para evaluar la eficiencia de los sistemas energéticos domésticos, ejecutando numerosas simulaciones en diferentes escenarios climáticos futuros. ^[6]

Los sistemas de fluidos pueden describirse mediante modelos cardiovasculares de elementos concentrados , utilizando voltaje para representar la presión y corriente para representar el flujo; ecuaciones idénticas a las de la representación del circuito eléctrico son válidas después de sustituir estas dos variables. Tales aplicaciones pueden, por ejemplo, estudiar la respuesta del sistema cardiovascular humano a la implantación de un dispositivo de asistencia ventricular . ^[7]

• Isomorfismo del sistema
• Reducción de pedidos de modelos

• Técnicas avanzadas de modelado y simulación de componentes magnéticos
• Suplemento IMTEK Mathematica (IMS), el Suplemento IMTEK Mathematica (IMS) de código abierto para modelado agrupado