Aberración óptica

Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes ) Este artículo se basa en gran medida en un artículo de la Encyclopædia Britannica Undécima Edición , que ya no está protegida por derechos de autor y que se publicó en 1911.Debe actualizarse para reflejar la historia o los estudios posteriores (incluidas las referencias, si las hubiera). Cuando haya completado la revisión, reemplace este aviso con una nota simple en la página de discusión de este artículo. ( Mayo de 2016 ) Es posible que sea necesario reescribir este artículo para cumplir con los estándares de calidad de Wikipedia .Puedes ayudar. La página de discusión puede contener sugerencias. ( Mayo de 2009 ) Este artículo se lee como un libro de texto .Por favor, mejore este artículo para que tenga un tono neutral y cumpla con los estándares de calidad de Wikipedia . ( Octubre de 2020 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En óptica , la aberración es una propiedad de los sistemas ópticos, como las lentes , que hace que la luz se disperse sobre una región del espacio en lugar de enfocarse en un punto. ^[1] Las aberraciones hacen que la imagen formada por una lente sea borrosa o distorsionada, y la naturaleza de la distorsión depende del tipo de aberración. La aberración se puede definir como una desviación del rendimiento de un sistema óptico con respecto a las predicciones de la óptica paraxial . ^[2] En un sistema de imágenes, ocurre cuando la luz de un punto de un objeto no converge en (o no diverge de) un solo punto después de la transmisión a través del sistema. Las aberraciones ocurren porque la teoría paraxial simple no es un modelo completamente preciso del efecto de un sistema óptico sobre la luz, en lugar de deberse a fallas en los elementos ópticos. ^[3]

Un sistema óptico de formación de imágenes con aberraciones producirá una imagen que no es nítida. Los fabricantes de instrumentos ópticos necesitan corregir los sistemas ópticos para compensar las aberraciones. Las aberraciones tienen un impacto especial en los telescopios, donde pueden degradar significativamente la calidad de los objetos celestes observados. Comprender y corregir estas imperfecciones ópticas es crucial para que los astrónomos logren observaciones claras y precisas. ^[4]

La aberración puede analizarse con técnicas de óptica geométrica . Los artículos sobre reflexión , refracción y cáusticos tratan las características generales de los rayos reflejados y refractados .

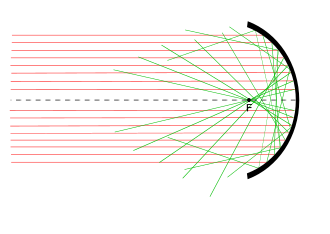
Con una lente ideal , la luz procedente de cualquier punto dado de un objeto pasaría a través de la lente y se concentraría en un único punto en el plano de la imagen (o, de forma más general, la superficie de la imagen ). Sin embargo, las lentes reales no enfocan la luz exactamente en un único punto, incluso cuando están perfectamente fabricadas. Estas desviaciones del rendimiento idealizado de la lente se denominan aberraciones de la lente.

Las aberraciones se dividen en dos clases: monocromáticas y cromáticas . Las aberraciones monocromáticas son causadas por la geometría de la lente o el espejo y ocurren tanto cuando la luz se refleja como cuando se refracta. Aparecen incluso cuando se utiliza luz monocromática , de ahí el nombre.

Las aberraciones cromáticas son causadas por la dispersión , la variación del índice de refracción de una lente con la longitud de onda . Debido a la dispersión, las diferentes longitudes de onda de la luz se enfocan en diferentes puntos. La aberración cromática no aparece cuando se utiliza luz monocromática.

Las aberraciones monocromáticas más comunes son:

• Desenfoque
• Aberración esférica
• Coma
• Astigmatismo
• Curvatura del campo
• Distorsión de la imagen

Aunque técnicamente el desenfoque es la aberración óptica de orden más bajo, generalmente no se considera una aberración de la lente, ya que se puede corregir moviendo la lente (o el plano de la imagen) para llevar el plano de la imagen al foco óptico de la lente.

Además de estas aberraciones, el pistón y la inclinación son efectos que modifican la posición del punto focal. El pistón y la inclinación no son aberraciones ópticas verdaderas, ya que cuando un frente de onda que de otro modo sería perfecto se altera mediante el pistón y la inclinación, seguirá formando una imagen perfecta y sin aberraciones, solo que desplazada a una posición diferente.

La aberración cromática se produce cuando diferentes longitudes de onda no se enfocan en el mismo punto. Los tipos de aberración cromática son:

• Aberración cromática axial (o "longitudinal")
• Aberración cromática lateral (o "transversal")

En un sistema óptico perfecto según la teoría clásica de la óptica , ^{[5] [6]} los rayos de luz que proceden de cualquier punto del objeto se unen en un punto imagen ; y por lo tanto el espacio del objeto se reproduce en un espacio imagen. La introducción de términos auxiliares simples, debido a Gauss , ^{[7] [8]} denominados distancias focales y planos focales , permite la determinación de la imagen de cualquier objeto para cualquier sistema. La teoría gaussiana, sin embargo, sólo es verdadera mientras los ángulos que forman todos los rayos con el eje óptico (el eje simétrico del sistema) sean infinitamente pequeños, es decir, con objetos, imágenes y lentes infinitesimales; en la práctica, estas condiciones pueden no cumplirse, y las imágenes proyectadas por sistemas no corregidos son, en general, mal definidas y a menudo borrosas si la apertura o el campo de visión exceden ciertos límites. ^[8]

Las investigaciones de James Clerk Maxwell ^[9] y Ernst Abbe ^{[nota 1]} demostraron que las propiedades de estas reproducciones, es decir, la posición relativa y la magnitud de las imágenes, no son propiedades especiales de los sistemas ópticos, sino consecuencias necesarias de la suposición (según Abbe) de la reproducción de todos los puntos de un espacio en puntos de imagen, y son independientes de la manera en que se efectúa la reproducción. Estos autores demostraron, sin embargo, que ningún sistema óptico puede justificar estas suposiciones, ya que son contradictorias con las leyes fundamentales de la reflexión y la refracción. En consecuencia, la teoría gaussiana sólo proporciona un método conveniente para aproximarse a la realidad; los sistemas ópticos realistas no alcanzan este ideal inalcanzable. Actualmente, todo lo que se puede lograr es la proyección de un solo plano sobre otro plano; pero incluso en esto, siempre ocurren aberraciones y puede ser poco probable que éstas sean corregidas por completo. ^[8]

Sea S (fig. 1) un sistema óptico cualquiera, los rayos que proceden de un punto de eje O bajo un ángulo u1 se unirán en el punto de eje O'1; y aquellos bajo un ángulo u2 en el punto de eje O'2. Si hay refracción en una superficie esférica colectiva, o a través de una lente positiva delgada, O'2 estará delante de O'1 siempre que el ángulo u2 sea mayor que u1 ( corrección insuficiente ); y a la inversa con una superficie o lentes dispersivas ( corrección excesiva ). La cáustica, en el primer caso, se asemeja al signo > (mayor que); en el segundo < (menor que). Si el ángulo u1 es muy pequeño, O'1 es la imagen gaussiana; y O'1 O'2 se denomina aberración longitudinal, y O'1R aberración lateral de los lápices con apertura u2. Si el lápiz con el ángulo u2 es el de máxima aberración de todos los lápices transmitidos, entonces en un plano perpendicular al eje en O'1 hay un disco circular de confusión de radio O'1R, y en un plano paralelo en O'2 otro de radio O'2R2; entre estos dos está situado el disco de menor confusión. ^[8]

La abertura más grande de los lápices que intervienen en la reproducción de O, es decir, el ángulo u, está determinada generalmente por el borde de una de las lentes o por un orificio en una placa delgada colocada entre, delante o detrás de las lentes del sistema. Este orificio se denomina diafragma ; Abbe utilizó el término diafragma tanto para el orificio como para el borde limitador de la lente. El componente S1 del sistema, situado entre el diafragma y el objeto O, proyecta una imagen del diafragma, llamada por Abbe pupila de entrada ; la pupila de salida es la imagen formada por el componente S2, que está colocado detrás del diafragma. Todos los rayos que salen de O y pasan por el diafragma pasan también por las pupilas de entrada y de salida, ya que son imágenes del diafragma. Como la abertura máxima de los lápices que salen de O es el ángulo u subtendido por la pupila de entrada en este punto, la magnitud de la aberración estará determinada por la posición y el diámetro de la pupila de entrada. Si el sistema está completamente detrás del diafragma, entonces éste es la pupila de entrada ( parada frontal ); si está completamente delante, es la pupila de salida ( parada posterior ). ^[8]

Si el punto objeto está infinitamente distante, todos los rayos recibidos por el primer miembro del sistema son paralelos y sus intersecciones, después de atravesar el sistema, varían según su altura de incidencia perpendicular, es decir, su distancia al eje. Esta distancia reemplaza al ángulo u en las consideraciones anteriores; y la apertura, es decir, el radio de la pupila de entrada, es su valor máximo. ^[8]

Si los rayos que salen de O (fig. 1) son concurrentes, no se sigue que los puntos en una porción de un plano perpendicular a O al eje también lo sean, incluso si la parte del plano es muy pequeña. A medida que aumenta el diámetro de la lente (es decir, con el aumento de la apertura), el punto vecino N se reproducirá, pero con aberraciones comparables en magnitud a ON. Estas aberraciones se evitan si, según Abbe, la condición del seno, sen u'1/sen u1=sen u'2/sen u2, se cumple para todos los rayos que reproducen el punto O. Si el punto objeto O está infinitamente distante, u1 y u2 se deben reemplazar por h1 y h2, las alturas perpendiculares de incidencia; la condición del seno entonces se convierte en sen u'1/h1=sen u'2/h2. Un sistema que cumple esta condición y está libre de aberraciones esféricas se llama aplanático (del griego a-, privativo, plann, a errante). Esta palabra fue utilizada por primera vez por Robert Blair para caracterizar un acromatismo superior y, posteriormente, por muchos escritores para denotar también la libertad de aberración esférica. ^[8]

Dado que la aberración aumenta con la distancia del rayo desde el centro de la lente, la aberración aumenta a medida que aumenta el diámetro de la lente (o, correspondientemente, con el diámetro de la apertura) y, por lo tanto, se puede minimizar reduciendo la apertura, a costa de reducir también la cantidad de luz que llega al plano de la imagen.

Un punto O (fig. 2) situado a una distancia finita del eje (o, en el caso de un objeto infinitamente distante, un punto que subtiende un ángulo finito en el sistema), en general, no se reproduce con nitidez si el haz de rayos que parte de él y atraviesa el sistema se estrecha infinitamente reduciendo el diafragma; un haz de este tipo está formado por los rayos que pueden pasar desde el punto del objeto a través de la pupila de entrada, ahora infinitamente pequeña. Se ve (sin tener en cuenta casos excepcionales) que el haz no se encuentra con la superficie refractante o reflectante en ángulo recto; por lo tanto, es astigmático (del gr. a-, privativo, stigmia, un punto). Si se llama eje del haz o rayo principal al rayo central que pasa por la pupila de entrada, se puede decir: los rayos del haz no se cortan en un punto, sino en dos líneas focales, que se puede suponer que forman ángulos rectos con el rayo principal; De estos, uno se encuentra en el plano que contiene el rayo principal y el eje del sistema, es decir, en la primera sección principal o sección meridional , y el otro en ángulo recto con él, es decir, en la segunda sección principal o sección sagital. Por lo tanto, no recibimos en un solo plano interceptor detrás del sistema, como, por ejemplo, una pantalla de enfoque, una imagen del punto objeto; por otro lado, en cada uno de los dos planos se forman por separado las líneas O' y O" (en los planos vecinos se forman elipses), y en un plano entre O' y O" un círculo de menor confusión. El intervalo O'O", denominado diferencia astigmática, aumenta, en general, con el ángulo W que forma el rayo principal OP con el eje del sistema, es decir, con el campo visual. A un plano del objeto corresponden dos superficies de imagen astigmáticas , que están en contacto en el punto del eje; en una de ellas se encuentran las líneas focales de la primera clase, en la otra las de la segunda. Los sistemas en los que coinciden las dos superficies astigmáticas se denominan anastigmáticos o estigmáticos. ^[8]

El astigmatismo fue probablemente obra de Sir Isaac Newton ; la posición de las líneas de la imagen astigmática fue determinada por Thomas Young; ^[10] y la teoría fue desarrollada por Allvar Gullstrand . ^{[11] [12] [8]} Una bibliografía de P. Culmann se encuentra en Die Bilderzeugung in optischen Instrumenten de Moritz von Rohr . ^{[13] [8]}

Al abrir más el tope, se producen desviaciones similares para los puntos laterales a las que ya se han discutido para los puntos axiales; pero en este caso son mucho más complicadas. El curso de los rayos en la sección meridional ya no es simétrico al rayo principal del lápiz; y en un plano de intersección aparece, en lugar de un punto luminoso, una mancha de luz, no simétrica respecto de un punto, y que a menudo muestra un parecido con un cometa con su cola dirigida hacia el eje o en dirección opuesta a él. De esta apariencia toma su nombre. La forma asimétrica del lápiz meridional, que antes era la única considerada, es coma en sentido estricto solamente; otros errores de coma han sido tratados por Arthur König y Moritz von Rohr, ^[13] y más tarde por Allvar Gullstrand. ^{[12] [8]}

Si se eliminan los errores anteriores, se unen las dos superficies astigmáticas y se obtiene una imagen nítida con una apertura amplia, sigue siendo necesario corregir la curvatura de la superficie de la imagen, especialmente cuando la imagen se recibe sobre una superficie plana, por ejemplo en fotografía. En la mayoría de los casos, la superficie es cóncava hacia el sistema. ^[8]

Incluso si la imagen es nítida, puede estar distorsionada en comparación con la proyección estenopeica ideal . En la proyección estenopeica, la ampliación de un objeto es inversamente proporcional a su distancia a la cámara a lo largo del eje óptico, de modo que una cámara que apunta directamente a una superficie plana reproduce esa superficie plana. La distorsión puede considerarse como un estiramiento de la imagen de forma no uniforme o, de manera equivalente, como una variación en la ampliación a lo largo del campo. Si bien la "distorsión" puede incluir la deformación arbitraria de una imagen, los modos de distorsión más pronunciados producidos por la óptica de imágenes convencional son la "distorsión de barril", en la que el centro de la imagen se amplía más que el perímetro (figura 3a). Lo inverso, en el que el perímetro se amplía más que el centro, se conoce como "distorsión de cojín" (figura 3b). Este efecto se denomina distorsión de la lente o distorsión de la imagen , y existen algoritmos para corregirlo.

Los sistemas libres de distorsión se denominan ortoscópicos (orthos, derecho, skopein, mirar) o rectilíneos (líneas rectas).

Esta aberración es muy distinta de la de la nitidez de la reproducción; en la reproducción no nítida, la cuestión de la distorsión surge si sólo se pueden reconocer partes del objeto en la figura. Si, en una imagen no nítida, una mancha de luz corresponde a un punto del objeto, el centro de gravedad de la mancha puede considerarse como el punto de la imagen, siendo este el punto donde el plano que recibe la imagen, por ejemplo, una pantalla de enfoque, intersecta el rayo que pasa por el medio del diafragma. Esta suposición está justificada si una imagen deficiente en la pantalla de enfoque permanece estacionaria cuando se disminuye la apertura; en la práctica, esto ocurre generalmente. Este rayo, llamado por Abbe rayo principal (que no debe confundirse con los rayos principales de la teoría de Gauss), pasa por el centro de la pupila de entrada antes de la primera refracción, y por el centro de la pupila de salida después de la última refracción. De esto se deduce que la exactitud del dibujo depende únicamente de los rayos principales; y es independiente de la nitidez o curvatura del campo de la imagen. Con referencia a la fig. 4, tenemos que O'Q'/OQ = a' tan w'/a tan w = 1/N, donde N es la escala o aumento de la imagen. Para que N sea constante para todos los valores de w, a' tan w'/a tan w también debe ser constante. Si la razón a'/a es suficientemente constante, como suele ser el caso, la relación anterior se reduce a la condición de Airy , es decir, tan w'/tan w = una constante. Esta relación simple (véase Camb. Phil. Trans., 1830, 3, pág. 1) se cumple en todos los sistemas que son simétricos con respecto a su diafragma (abreviadamente llamados objetivos simétricos u holosimétricos ), o que consisten en dos componentes iguales, pero de diferente tamaño, colocados a partir del diafragma en la razón de su tamaño, y que presentan la misma curvatura con respecto a él (objetivos hemisimétricos); en estos sistemas tan w' / tan w = 1. ^[8]

La constancia de a'/a necesaria para que se cumpla esta relación fue señalada por RH Bow (Brit. Journ. Photog., 1861) y Thomas Sutton (Photographic Notes, 1862); ha sido tratada por O. Lummer y por M. von Rohr (Zeit. f. Instrumentenk., 1897, 17, y 1898, 18, p. 4). Requiere que el centro del diafragma se reproduzca en los centros de las pupilas de entrada y salida sin aberración esférica. M. von Rohr demostró que para sistemas que no cumplen ni la condición de Airy ni la de Bow-Sutton, la relación a' cos w'/a tan w será constante para una distancia del objeto. Esta condición combinada se cumple exactamente con objetivos holosimétricos que reproducen con la escala 1, y con objetivos hemisimétricos, si la escala de reproducción es igual a la relación de los tamaños de los dos componentes. ^[8]

Los perfiles de frente de onda circular asociados con aberraciones pueden modelarse matemáticamente utilizando polinomios de Zernike . Desarrollados por Frits Zernike en la década de 1930, los polinomios de Zernike son ortogonales sobre un círculo de radio unitario. Un perfil de frente de onda aberrado complejo puede ajustarse mediante curvas con polinomios de Zernike para producir un conjunto de coeficientes de ajuste que representan individualmente diferentes tipos de aberraciones. Estos coeficientes de Zernike son linealmente independientes , por lo que las contribuciones de aberraciones individuales a un frente de onda general pueden aislarse y cuantificarse por separado.

Existen polinomios de Zernike pares e impares . Los polinomios de Zernike pares se definen como

${\displaystyle Z_{n}^{m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\cos(m\,\phi )\!}$

y los polinomios de Zernike impares como

${\displaystyle Z_{n}^{-m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\sin(m\,\phi ),\!}$

donde m y n son números enteros no negativos con , Φ es el ángulo azimutal en radianes y ρ es la distancia radial normalizada. Los polinomios radiales no tienen dependencia azimutal y se definen como${\displaystyle n\geq m}$ $Estilo de visualización R_{n}^{m}}$

${\displaystyle R_{n}^{m}(\rho )=\!\sum _{k=0}^{(nm)/2}\!\!\!{\frac {(-1)^{k}\,(nk)!}{k!\,((n+m)/2-k)!\,((nm)/2-k)!}}\;\rho ^{n-2\,k}\quad {\mbox{si }}nm{\mbox{ es par}}}$

y si es impar.${\displaystyle R_{n}^{m}(\rho )=0}$${\estilo de visualización nm}$

Los primeros polinomios de Zernike, multiplicados por sus respectivos coeficientes de ajuste, son: ^[14]

${\displaystyle a_{0}\times 1}$	"Pistón", igual al valor medio del frente de onda
${\displaystyle a_{1}\times \rho \cos(\phi )}$	"X-Tilt", la desviación del haz general en la dirección sagital
${\displaystyle a_{2}\times \rho \sin(\phi )}$	"Y-Tilt", la desviación del haz general en la dirección tangencial
${\displaystyle a_{3}\times (2\rho ^{2}-1)}$	"Desenfoque", un frente de onda parabólico que resulta de estar fuera de foco
${\displaystyle a_{4}\times \rho ^{2}\cos(2\phi )}$	"Astigmatismo 0°", una forma cilíndrica a lo largo del eje X o Y
${\displaystyle a_{5}\times \rho ^{2}\sin(2\phi )}$	"Astigmatismo de 45°", una forma cilíndrica orientada a ±45° desde el eje X
${\displaystyle a_{6}\times (3\rho ^{2}-2)\rho \cos(\phi )}$	"X-Coma", imagen cómica que se proyecta en dirección horizontal
${\displaystyle a_{7}\times (3\rho ^{2}-2)\rho \sin(\phi )}$	"Y-Coma", imagen cómica que se proyecta en dirección vertical
${\displaystyle a_{8}\times (6\rho ^{4}-6\rho ^{2}+1)}$	"Aberración esférica de tercer orden"

donde es el radio pupilar normalizado con , es el ángulo azimutal alrededor de la pupila con , y los coeficientes de ajuste son los errores del frente de onda en longitudes de onda.${\estilo de visualización \rho}$${\displaystyle 0\leq \rho \leq 1}$${\estilo de visualización \phi}$${\displaystyle 0\leq \phi \leq 2\pi }$${\displaystyle a_{0},\ldots ,a_{8}}$

Al igual que en la síntesis de Fourier que utiliza senos y cosenos , un frente de onda puede representarse perfectamente mediante una cantidad suficientemente grande de polinomios de Zernike de orden superior. Sin embargo, los frentes de onda con gradientes muy pronunciados o una estructura de frecuencia espacial muy alta , como los producidos por la propagación a través de la turbulencia atmosférica o los campos de flujo aerodinámicos , no se modelan bien mediante polinomios de Zernike, que tienden a filtrar por paso bajo la definición espacial fina en el frente de onda. En este caso, otros métodos de ajuste, como los fractales o la descomposición en valores singulares, pueden producir mejores resultados de ajuste.

Los polinomios circulares fueron introducidos por Frits Zernike para evaluar la imagen puntual de un sistema óptico aberrado teniendo en cuenta los efectos de la difracción . La imagen puntual perfecta en presencia de difracción ya había sido descrita por Airy , ya en 1835. Se necesitaron casi cien años para llegar a una teoría y modelado integral de la imagen puntual de sistemas aberrados (Zernike y Nijboer). El análisis de Nijboer y Zernike describe la distribución de intensidad cerca del plano focal óptimo. Recientemente se desarrolló una teoría extendida que permite el cálculo de la amplitud e intensidad de la imagen puntual sobre un volumen mucho mayor en la región focal (teoría extendida de Nijboer-Zernike). Esta teoría extendida de Nijboer-Zernike de la formación de imágenes puntuales o "función de propagación de puntos" ha encontrado aplicaciones en la investigación general sobre la formación de imágenes, especialmente para sistemas con una alta apertura numérica , y en la caracterización de sistemas ópticos con respecto a sus aberraciones. ^[15]

La reseña precedente de los diversos errores de reproducción pertenece a la teoría de las aberraciones de Abbe, en la que se tratan por separado determinadas aberraciones; es muy adecuada para las necesidades prácticas, pues en la construcción de un instrumento óptico se busca eliminar ciertos errores, cuya selección está justificada por la experiencia. Sin embargo, en el sentido matemático, esta selección es arbitraria; la reproducción de un objeto finito con una abertura finita implica, con toda probabilidad, un número infinito de aberraciones. Este número sólo es finito si se supone que el objeto y la abertura son infinitamente pequeños de un cierto orden ; y con cada orden de pequeñez infinita, es decir, con cada grado de aproximación a la realidad (a objetos y aberturas finitos), se asocia un cierto número de aberraciones. Esta conexión sólo la proporcionan las teorías que tratan las aberraciones de forma general y analítica por medio de series indefinidas. ^[8]

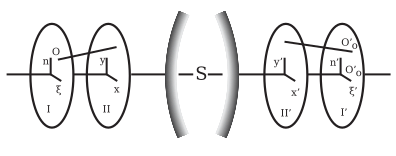
Un rayo que procede de un punto O (fig. 5) puede definirse por las coordenadas (ξ, η). De este punto O en un plano I, perpendicular al eje, y otras dos coordenadas (x, y), el punto en el que el rayo corta la pupila de entrada, es decir, el plano II. De manera similar, el rayo imagen correspondiente puede definirse por los puntos (ξ', η') y (x', y'), en los planos I' y II'. Los orígenes de estos cuatro sistemas de coordenadas planas pueden ser colineales con el eje del sistema óptico; y los ejes correspondientes pueden ser paralelos. Cada una de las cuatro coordenadas ξ', η', x', y' son funciones de ξ, η, x, y; y si se supone que el campo de visión y la apertura son infinitamente pequeños, entonces ξ, η, x, y son del mismo orden de infinitesimales; En consecuencia, desarrollando ξ', η', x', y' en potencias ascendentes de ξ, η, x, y, se obtienen series en las que sólo es necesario considerar las potencias más bajas. Se ve fácilmente que si el sistema óptico es simétrico, los orígenes de los sistemas de coordenadas colineales con el eje óptico y los ejes correspondientes paralelos, entonces al cambiar los signos de ξ, η, x, y, los valores ξ', η', x', y' deben cambiar igualmente su signo, pero conservar sus valores aritméticos; esto significa que las series están restringidas a las potencias impares de las variables no marcadas. ^[8]

La naturaleza de la reproducción consiste en que los rayos que parten de un punto O se unen en otro punto O'; en general, esto no será así, pues ξ', η' varían si ξ, η son constantes, pero x, y variables. Puede suponerse que los planos I' y II' están dibujados donde las imágenes de los planos I y II están formadas por rayos próximos al eje por las reglas gaussianas ordinarias; y por una extensión de estas reglas, no correspondiendo, sin embargo, a la realidad, podría construirse la imagen gaussiana del punto O' ₀ , con coordenadas ξ' ₀ , η' ₀ , del punto O a cierta distancia del eje. Escribiendo Dξ'=ξ'-ξ' ₀ y Dη'=η'-η' ₀ , entonces Dξ' y Dη' son las aberraciones pertenecientes a ξ, η y x, y, y son funciones de estas magnitudes que, cuando se desarrollan en serie, contienen sólo potencias impares, por las mismas razones que se dieron anteriormente. Debido a las aberraciones de todos los rayos que pasan por O, se formará en el plano I' una mancha de luz, cuyo tamaño depende de las potencias más bajas de ξ, η, x, y que contienen las aberraciones. Estos grados, llamados por J. Petzval ^[16] los órdenes numéricos de la imagen, son, en consecuencia, sólo potencias impares; la condición para la formación de una imagen del orden m es que en la serie para Dξ' y Dη' los coeficientes de las potencias de los grados 3º, 5º...(m-2)º deben anularse. Como las imágenes de la teoría de Gauss son de tercer orden, el siguiente problema es obtener una imagen de quinto orden, o hacer que los coeficientes de las potencias de tercer grado sean cero. Esto requiere satisfacer cinco ecuaciones; en otras palabras, hay cinco alteraciones de tercer orden, cuyo desvanecimiento produce una imagen de quinto orden. ^[8]

La expresión de estos coeficientes en términos de las constantes del sistema óptico, es decir, los radios, espesores, índices de refracción y distancias entre las lentes, fue resuelta por L. Seidel ; ^[17] en 1840, J. Petzval construyó su objetivo de retrato, a partir de cálculos similares que nunca han sido publicados. ^[18] La teoría fue elaborada por S. Finterswalder, ^[19] quien también publicó un artículo póstumo de Seidel que contenía una breve visión de su trabajo; ^[20] una forma más simple fue dada por A. Kerber. ^[21] A. Konig y M. von Rohr ^{[22] : 317–323} han representado el método de Kerber, y han deducido las fórmulas de Seidel a partir de consideraciones geométricas basadas en el método de Abbe, y han interpretado los resultados analíticos geométricamente. ^{[22] : 212–316  [8]}

Las aberraciones también pueden expresarse mediante la función característica del sistema y sus coeficientes diferenciales, en lugar de por los radios, etc., de las lentes; estas fórmulas no son inmediatamente aplicables, pero dan, sin embargo, la relación entre el número de aberraciones y el orden. Sir William Rowan Hamilton (British Assoc. Report, 1833, p. 360) dedujo así las aberraciones del tercer orden; y en épocas posteriores el método fue seguido por Clerk Maxwell ( Proc. London Math. Soc., 1874-1875; (ver también los tratados de RS Heath y LA Herman), M. Thiesen ( Berlin. Akad. Sitzber., 1890, 35, p. 804), H. Bruns ( Leipzig. Math. Phys. Ber., 1895, 21, p. 410), y particularmente exitosamente por K. Schwarzschild ( Göttingen. Akad. Abhandl., 1905, 4, No. 1), quien así descubrió las aberraciones del quinto orden (de las cuales hay nueve), y posiblemente la prueba más corta de las fórmulas prácticas (Seidel). A. Gullstrand (vide supra, y Ann. d. Phys., 1905, 18, p. 941) fundó su teoría de las aberraciones en la geometría diferencial. de superficies. ^[8]

Las aberraciones de tercer orden son: (1) aberración del punto del eje; (2) aberración de puntos cuya distancia del eje es muy pequeña, menor que la de tercer orden — la desviación de la condición sinusoidal y la coma aquí caen juntas en una clase; (3) astigmatismo; (4) curvatura del campo; (5) distorsión. ^[8]

1. La aberración de tercer orden de los puntos del eje se trata en todos los libros de texto sobre óptica. Es muy importante en el diseño de telescopios. En los telescopios, la apertura se suele tomar como el diámetro lineal del objetivo. No es lo mismo que la apertura del microscopio, que se basa en la pupila de entrada o el campo de visión visto desde el objeto y se expresa como una medida angular. Las aberraciones de orden superior en el diseño de telescopios se pueden ignorar en su mayor parte. En el caso de los microscopios, no se puede ignorar. Para una sola lente de espesor muy pequeño y una potencia dada, la aberración depende de la relación de los radios r:r', y es un mínimo (pero nunca cero) para un cierto valor de esta relación; varía inversamente con el índice de refracción (la potencia de la lente permanece constante). La aberración total de dos o más lentes muy delgadas en contacto, que es la suma de las aberraciones individuales, puede ser cero. Esto también es posible si las lentes tienen el mismo signo algebraico. De las lentes delgadas positivas con n=1,5, se necesitan cuatro para corregir la aberración esférica de tercer orden. Sin embargo, estos sistemas no tienen una gran importancia práctica. En la mayoría de los casos, se combinan dos lentes delgadas, una de las cuales tiene una aberración positiva tan fuerte ( corrección insuficiente, vide supra) como la otra una negativa; la primera debe ser una lente positiva y la segunda una lente negativa; sin embargo, las potencias pueden diferir, de modo que se mantenga el efecto deseado de la lente. Generalmente es una ventaja asegurar un gran efecto refractivo con varias lentes de mayor potencia que con una sola. Con una, y también con varias, e incluso con un número infinito de lentes delgadas en contacto, no se pueden reproducir más de dos puntos de eje sin aberración de tercer orden. La ausencia de aberración para dos puntos de eje, uno de los cuales está infinitamente distante, se conoce como condición de Herschel. Todas estas reglas son válidas, en la medida en que no se deben tener en cuenta los espesores y las distancias de las lentes. ^[8]
2. La condición de ausencia de coma en el tercer orden también es importante para los objetivos de los telescopios; se conoce como condición de Fraunhofer . (4) Después de eliminar la aberración en el eje, la coma y el astigmatismo, la relación para la planitud del campo en el tercer orden se expresa mediante la ecuación de Petzval, S1/r(n'−n) = 0, donde r es el radio de una superficie refractante, n y n' los índices de refracción de los medios vecinos y S el signo de la suma para todas las superficies refractantes. ^[8]

El problema clásico de la formación de imágenes es reproducir perfectamente un plano finito (el objeto) en otro plano (la imagen) a través de una apertura finita. Es imposible hacerlo perfectamente para más de un par de planos (esto fue demostrado con creciente generalidad por Maxwell en 1858, por Bruns en 1895 y por Carathéodory en 1926, véase el resumen en Walther, A., J. Opt. Soc. Am. A 6 , 415–422 (1989)). Sin embargo, para un solo par de planos (por ejemplo, para un solo ajuste de enfoque de un objetivo), el problema puede, en principio, resolverse perfectamente. Ejemplos de un sistema teóricamente perfecto de este tipo incluyen la lente de Luneburg y el ojo de pez de Maxwell .

Los métodos prácticos resuelven este problema con una precisión que, en la mayoría de los casos, es suficiente para el propósito específico de cada tipo de instrumento. El problema de encontrar un sistema que reproduzca un objeto dado en un plano dado con un aumento dado (en la medida en que se deben tener en cuenta las aberraciones) podría abordarse mediante la teoría de aproximación; sin embargo, en la mayoría de los casos, las dificultades analíticas eran demasiado grandes para los métodos de cálculo antiguos, pero pueden mejorarse mediante la aplicación de sistemas informáticos modernos. Sin embargo, se han obtenido soluciones en casos especiales. ^[24] En la actualidad, los constructores casi siempre emplean el método inverso: componen un sistema a partir de ciertas experiencias, a menudo bastante personales, y prueban, mediante el cálculo trigonométrico de las trayectorias de varios rayos, si el sistema da la reproducción deseada (se dan ejemplos en A. Gleichen, Lehrbuch der geometrischen Optik , Leipzig y Berlín, 1902). Los radios, los espesores y las distancias se modifican continuamente hasta que los errores de la imagen se vuelven suficientemente pequeños. Con este método se investigan únicamente algunos errores de reproducción, especialmente algunos de los elementos mencionados anteriormente o todos ellos. La teoría de la aproximación analítica se suele emplear de forma provisional, ya que su precisión no suele ser suficiente. ^[8]

Para que la aberración esférica y la desviación de la condición seno sean pequeñas en toda la abertura, se da a un rayo con un ángulo de abertura finito u* (anchura de objetos infinitamente distantes: con una altura de incidencia finita h*) la misma distancia de intersección y la misma relación seno que a un rayo vecino al eje (u* o h* no pueden ser mucho menores que la abertura más grande U o H que se utilizará en el sistema). Los rayos con un ángulo de abertura menor que u* no tendrían la misma distancia de intersección y la misma relación seno; estas desviaciones se denominan zonas y el constructor intenta reducirlas al mínimo. Lo mismo se aplica a los errores que dependen del ángulo del campo de visión, w: el astigmatismo, la curvatura del campo y la distorsión se eliminan para un valor definido, w*, las zonas de astigmatismo, curvatura del campo y distorsión, corresponden a valores menores de w. El óptico práctico denomina a estos sistemas corregidos en función del ángulo de apertura u* (altura de incidencia h*) o del ángulo del campo de visión w*. La aberración esférica y los cambios de las relaciones sinusoidales se representan a menudo gráficamente como funciones de la apertura, de la misma manera que las desviaciones de dos superficies de imagen astigmáticas del plano de imagen del punto del eje se representan como funciones de los ángulos del campo de visión. ^[8]

La forma final de un sistema práctico se basa, por tanto, en un compromiso: la ampliación de la apertura da como resultado una disminución del campo de visión disponible, y viceversa. Pero la apertura mayor dará la resolución mayor. Los siguientes pueden considerarse típicos: ^[8]

1. Apertura máxima; las correcciones necesarias son: para el punto del eje y la condición del seno; los errores del campo de visión casi no se tienen en cuenta; ejemplo: objetivos de microscopio de alta potencia.
2. Lente gran angular ; las correcciones necesarias son: astigmatismo, curvatura de campo y distorsión; los errores de apertura solo se consideran ligeramente; ejemplos: objetivos y oculares fotográficos de ángulo más amplio.
   Entre estos ejemplos extremos se encuentra el objetivo normal : éste está más corregido en cuanto a apertura; los objetivos para grupos, más en cuanto al campo de visión.
3. Las lentes de enfoque largo tienen campos de visión pequeños y las aberraciones en el eje son muy importantes. Por lo tanto, las zonas se mantendrán lo más pequeñas posible y el diseño debe enfatizar la simplicidad. Por eso, estas lentes son las mejores para el cálculo analítico.

En los sistemas ópticos compuestos por lentes, la posición, magnitud y errores de la imagen dependen de los índices de refracción del vidrio empleado (ver Lente (óptica) y Aberración monocromática, arriba). Como el índice de refracción varía con el color o la longitud de onda de la luz (ver dispersión ), se deduce que un sistema de lentes (sin corregir) proyecta imágenes de diferentes colores en lugares y tamaños algo diferentes y con diferentes aberraciones; es decir, hay diferencias cromáticas de las distancias de intersección, de aumentos y de aberraciones monocromáticas. Si se emplea luz mixta (por ejemplo, luz blanca), se forman todas estas imágenes y causan una confusión, llamada aberración cromática; por ejemplo, en lugar de un margen blanco sobre un fondo oscuro, se percibe un margen coloreado o un espectro estrecho. La ausencia de este error se denomina acromatismo, y un sistema óptico así corregido se denomina acromático. Se dice que un sistema está cromáticamente subcorregido cuando muestra el mismo tipo de error cromático que una lente positiva delgada; de lo contrario, se dice que está sobrecorregido. ^[8]

Si, en primer lugar, se desprecian las aberraciones monocromáticas, es decir, se acepta la teoría de Gauss, entonces toda reproducción está determinada por las posiciones de los planos focales y la magnitud de las distancias focales, o si las distancias focales, como sucede ordinariamente, son iguales, por tres constantes de reproducción. Estas constantes están determinadas por los datos del sistema (radios, espesores, distancias, índices, etc., de las lentes); por lo tanto, su dependencia del índice de refracción y, en consecuencia, del color, ^[8] es calculable. ^[25] Los índices de refracción para diferentes longitudes de onda deben ser conocidos para cada tipo de vidrio utilizado. De esta manera se mantienen las condiciones de que cualquier constante de reproducción sea igual para dos colores diferentes, es decir, esta constante está acromatizada. Por ejemplo, es posible, con una lente gruesa en el aire, acromatizar la posición de un plano focal de la magnitud de la distancia focal. Si las tres constantes de reproducción están acromatizadas, entonces la imagen gaussiana para todas las distancias de los objetos es la misma para los dos colores, y se dice que el sistema está en acromatismo estable. ^[8]

En la práctica, es más ventajoso (según Abbe) determinar la aberración cromática (por ejemplo, la de la distancia de intersección) para una posición fija del objeto, y expresarla mediante una suma en la que cada componente contiene la cantidad debida a cada superficie refractante. ^{[26] [27] [8]} En un plano que contiene el punto de imagen de un color, otro color produce un disco de confusión; esto es similar a la confusión causada por dos zonas en la aberración esférica. Para objetos infinitamente distantes, el radio del disco cromático de confusión es proporcional a la apertura lineal e independiente de la distancia focal ( vide supra , Aberración monocromática del punto del eje ); y dado que este disco se vuelve menos dañino con una imagen creciente de un objeto dado, o con una distancia focal creciente, se deduce que el deterioro de la imagen es proporcional a la relación entre la apertura y la distancia focal, es decir, la apertura relativa. (Esto explica las distancias focales gigantescas en boga antes del descubrimiento del acromatismo.) ^[8]

Ejemplos:

Newton no se dio cuenta de la existencia de medios de diferente poder dispersivo requeridos por el acromatismo, por lo que construyó grandes reflectores en lugar de refractores. James Gregory y Leonhard Euler llegaron a la conclusión correcta a partir de una concepción errónea del acromatismo del ojo; esto fue determinado por Chester More Hall en 1728, Klingenstierna en 1754 y por Dollond en 1757, quienes construyeron los famosos telescopios acromáticos. (Véase telescopio .) ^[8]

El vidrio con un poder dispersivo más débil (mayor ) se denomina vidrio crown ; el que tiene un poder dispersivo mayor, vidrio flint . Para la construcción de una lente colectiva acromática ( positiva) se deduce, por medio de la ecuación (4), que se debe elegir una lente colectiva I. de vidrio crown y una lente dispersiva II. de vidrio flint; esta última, aunque más débil, corrige cromáticamente a la otra por su mayor poder dispersivo. Para una lente dispersiva acromática se debe adoptar lo inverso. Este es, en la actualidad, el tipo ordinario, por ejemplo, de objetivo de telescopio; los valores de los cuatro radios deben satisfacer las ecuaciones (2) y (4). También se pueden postular otras dos condiciones: una es siempre la eliminación de la aberración en el eje; la segunda, o bien la condición de Herschel o de Fraunhofer, siendo esta última la mejor vide supra, Aberración monocromática ). En la práctica, sin embargo, a menudo es más útil evitar la segunda condición haciendo que las lentes tengan contacto, es decir, radios iguales. Según P. Rudolph (Eder's Jahrb. f. Photog., 1891, 5, pág. 225; 1893, 7, pág. 221), los objetivos cementados de lentes delgadas permiten la eliminación de la aberración esférica en el eje, si, como antes, la lente colectiva tiene un índice de refracción menor; por otro lado, permiten la eliminación del astigmatismo y la curvatura del campo, si la lente colectiva tiene un índice de refracción mayor (esto se desprende de la ecuación de Petzval; ver L. Seidel, Astr. Nachr., 1856, pág. 289). Si el sistema cementado es positivo, entonces la lente más potente debe ser positiva; y, según (4), a la mayor potencia pertenece el poder dispersivo más débil (mayor ), es decir, el vidrio crown; En consecuencia, el vidrio crown debe tener el mayor índice de refracción para imágenes astigmáticas y planas. Sin embargo, en todos los tipos de vidrio anteriores, el poder dispersivo aumentaba con el índice de refracción; es decir, disminuía a medida que aumentaba; pero algunos de los vidrios Jena de E. Abbe y O. Schott eran vidrios crown de alto índice de refracción, y los sistemas acromáticos de tales vidrios crown, con vidrios flint de índice de refracción más bajo, se denominan los nuevos acromáticos, y fueron utilizados por P. Rudolph en los primeros anastigmatos (objetivos fotográficos). ^[8]${\displaystyle v}$${\displaystyle f}$${\displaystyle v}$${\displaystyle v}$${\displaystyle n}$

En lugar de hacer que desaparezca, se le puede asignar un valor determinado que produzca, mediante la adición de las dos lentes, cualquier desviación cromática deseada, por ejemplo, suficiente para eliminar una presente en otras partes del sistema. Si las lentes I. y II. están cementadas y tienen el mismo índice de refracción para un color, entonces su efecto para ese color es el de una lente de una sola pieza; mediante esta descomposición de una lente se puede hacer cromática o acromática a voluntad, sin alterar su efecto esférico. Si su efecto cromático ( ) es mayor que el de la misma lente, al estar hecha del vidrio más dispersivo de los dos empleados, se denomina hipercromática. ^[8]${\displaystyle df}$${\displaystyle df/f}$

Para dos lentes delgadas separadas por una distancia, la condición para el acromatismo es ; si (por ejemplo, si las lentes están hechas del mismo vidrio), esto se reduce a , conocida como la condición para oculares. ^[8]${\displaystyle D}$${\displaystyle D=v_{1}f_{1}+v_{2}f_{2}}$${\displaystyle v_{1}=v_{2}}$${\displaystyle D=(f_{1}+f_{2})/2}$

Si una constante de reproducción, por ejemplo la distancia focal, se hace igual para dos colores, entonces no es la misma para otros colores, si se utilizan dos vidrios diferentes. Por ejemplo, la condición de acromatismo (4) para dos lentes delgadas en contacto se cumple sólo en una parte del espectro, ya que varía dentro del espectro. Este hecho fue establecido por primera vez por J. Fraunhofer, quien definió los colores por medio de las líneas oscuras en el espectro solar y demostró que la razón de la dispersión de dos vidrios varía alrededor del 20% del rojo al violeta (la variación para el vidrio y el agua es de alrededor del 50%). Por lo tanto, si para dos colores, a y b, entonces para un tercer color, c, la distancia focal es diferente; es decir, si c está entre a y b, entonces y viceversa; estos resultados algebraicos se siguen del hecho de que hacia el rojo predomina la dispersión del vidrio crown positivo, hacia el violeta la del sílex negativo. Estos errores cromáticos de los sistemas, que son acromáticos para dos colores, se denominan espectro secundario y dependen de la apertura y de la distancia focal de la misma manera que los errores cromáticos primarios. ^[8]${\displaystyle dn_{2}/dn_{1}}$${\displaystyle f_{a}=f_{b}=f}$${\displaystyle f_{c}<f}$

En la figura. 6, tomado de Theorie und Geschichte des photographischen Objectivs de M. von Rohr , las abscisas son longitudes focales y las ordenadas, longitudes de onda. Las líneas de Fraunhofer utilizadas se muestran en la tabla adjunta. ^[8]

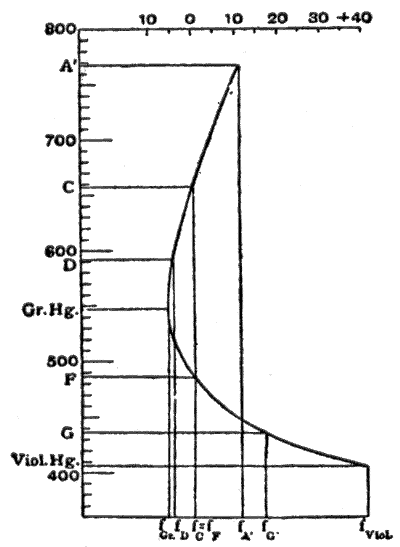
Las longitudes focales se hacen iguales para las líneas C y F. En la vecindad de 550 nm la tangente a la curva es paralela al eje de longitudes de onda; y la longitud focal varía menos en una gama bastante grande de color, por lo tanto en esta vecindad la unión de colores es mejor. Además, esta región del espectro es la que aparece más brillante al ojo humano, y en consecuencia esta curva del espectro secundario, obtenida al hacer , es, según los experimentos de Sir GG Stokes (Proc. Roy. Soc., 1878), la más adecuada para instrumentos visuales ( acromatismo óptico ). De manera similar, para los sistemas utilizados en fotografía, el vértice de la curva de color debe colocarse en la posición de la sensibilidad máxima de las placas; generalmente se supone que está en G'; y para lograr esto, las líneas F y de mercurio violeta se unen. Este artificio se adopta especialmente en objetivos para fotografía astronómica ( acromatismo actínico puro ). Sin embargo, en la fotografía ordinaria existe el siguiente inconveniente: la imagen en la pantalla de enfoque y el ajuste correcto de la placa fotográfica sensible no están en registro; en la fotografía astronómica esta diferencia es constante, pero en otros tipos depende de la distancia de los objetos. Por este motivo, las líneas D y G' están unidas en los objetivos fotográficos ordinarios; la imagen óptica y la actínica son cromáticamente inferiores, pero ambas se encuentran en el mismo lugar; y, en consecuencia, la mejor corrección se encuentra en F (esto se conoce como corrección actínica o libertad de foco químico ). ^[8]${\displaystyle f_{C}=f_{F}}$

Si en dos lentes en contacto hay las mismas distancias focales para tres colores a, b y c, es decir , entonces la dispersión parcial relativa debe ser igual para los dos tipos de vidrio empleados. Esto se deduce considerando la ecuación (4) para los dos pares de colores ac y bc. Hasta hace poco no se conocían vidrios con un grado proporcional de absorción; pero R. Blair (Trans. Edin. Soc., 1791, 3, p. 3), P. Barlow y FS Archer superaron la dificultad construyendo lentes fluidas entre paredes de vidrio. Fraunhofer preparó vidrios que reducían el espectro secundario; pero el éxito permanente sólo estuvo asegurado con la introducción de los vidrios de Jena por E. Abbe y O. Schott. Al utilizar vidrios que no tienen dispersión proporcional, la desviación de un tercer color puede eliminarse mediante dos lentes, si se deja un intervalo entre ellas; o mediante tres lentes en contacto, que pueden no estar compuestas todas por los vidrios antiguos. Al unir tres colores se deriva un acromatismo de un orden superior ; Todavía hay un espectro terciario residual, pero siempre se puede despreciar. ^[8]${\displaystyle f_{a}=f_{b}=f_{c}=f}$${\displaystyle (n_{c}-n_{b})(n_{a}-n_{b})}$

La teoría gaussiana es sólo una aproximación; todavía se producen aberraciones monocromáticas o esféricas, que serán diferentes para los distintos colores; y si se compensaran para un color, la imagen de otro color resultaría perturbadora. La más importante es la diferencia cromática de aberración del punto del eje, que sigue presente para perturbar la imagen, después de que los rayos paraaxiales de diferentes colores se unen mediante una combinación apropiada de vidrios. Si se corrige un sistema colectivo para el punto del eje para una longitud de onda definida, entonces, debido a la mayor dispersión en los componentes negativos - los vidrios de sílex - surgirá una sobrecorrección para las longitudes de onda más cortas (siendo este el error de los componentes negativos) y una subcorrección para las longitudes de onda más largas (el error de las lentes de vidrio Crown que predominan en el rojo). Este error fue tratado por Jean le Rond d'Alembert y, con especial detalle, por CF Gauss. Aumenta rápidamente con la apertura y es más importante con aperturas medianas que el espectro secundario de los rayos paraaxiales; En consecuencia, la aberración esférica debe eliminarse para dos colores, y si esto es imposible, entonces debe eliminarse para aquellas longitudes de onda particulares que son más efectivas para el instrumento en cuestión (una representación gráfica de este error se da en M. von Rohr, Theorie und Geschichte des photographischen Objectivs ). ^[8]

La condición para la reproducción de un elemento de superficie en lugar de un punto reproducido nítidamente es que la constante de la relación seno también debe cumplirse con grandes aberturas para varios colores. E. Abbe logró calcular objetivos de microscopio libres de error del punto del eje y que satisfacían la condición seno para varios colores, que por lo tanto, según su definición, eran aplanáticos para varios colores ; a estos sistemas los denominó apocromáticos . Sin embargo, si bien el aumento de las zonas individuales es el mismo, no es el mismo para el rojo que para el azul; y existe una diferencia cromática de aumento. Esta es producida en la misma cantidad, pero en sentido opuesto, por los oculares que Abbe utilizó con estos objetivos ( oculares de compensación ), de modo que se elimina en la imagen de todo el microscopio. Los mejores objetivos de telescopio y los objetivos fotográficos destinados al trabajo en tres colores también son apocromáticos, incluso si no poseen exactamente la misma calidad de corrección que los objetivos de microscopio. Las diferencias cromáticas de otros errores de reproducción rara vez tienen importancia práctica. ^[8]

• Aberraciones del ojo
• Telescopio óptico § Las cinco aberraciones de Seidel
• Codificación de frente de onda

• Objetivos del microscopio: sección de aberraciones ópticas del sitio web Molecular Expressions , Michael W. Davidson, Mortimer Abramowitz, Olympus America Inc. y la Universidad Estatal de Florida