Sistema eutéctico

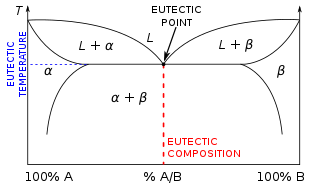
Un sistema eutéctico o mezcla eutéctica ( / j uː ˈ t ɛ k t ɪ k / yoo- TEK -tik ) ^[1] es un tipo de mezcla homogénea que tiene un punto de fusión inferior al de los constituyentes. ^[2] El punto de fusión más bajo posible en todas las proporciones de mezcla de los constituyentes se denomina temperatura eutéctica . En un diagrama de fases , la temperatura eutéctica se ve como el punto eutéctico (ver gráfico a la derecha). ^[3]

Las proporciones de mezclas no eutécticas tienen diferentes temperaturas de fusión para sus distintos constituyentes, ya que la red de un componente se derretirá a una temperatura más baja que la del otro. Por el contrario, a medida que una mezcla no eutéctica se enfría, cada uno de sus componentes se solidifica en una red a una temperatura diferente, hasta que toda la masa es sólida.

No todas las aleaciones binarias tienen puntos eutécticos, ya que los electrones de valencia de las especies componentes no siempre son compatibles ^{[ aclaración necesaria ]} en cualquier proporción de mezcla para formar un nuevo tipo de red cristalina conjunta. Por ejemplo, en el sistema plata-oro, la temperatura de fusión ( liquidus ) y la temperatura de congelación ( solidus ) "se encuentran en los puntos finales del elemento puro del eje de proporción atómica mientras que se separan ligeramente en la región de mezcla de este eje". ^[4]

En el mundo real, las propiedades eutécticas se pueden utilizar de manera ventajosa en procesos como la unión eutéctica , donde los chips de silicio se unen a sustratos chapados en oro con ultrasonidos , y las aleaciones eutécticas resultan valiosas en aplicaciones tan diversas como la soldadura, la soldadura fuerte, la fundición de metales, la protección eléctrica, los sistemas de rociadores contra incendios y los sustitutos no tóxicos del mercurio.

El término eutéctico fue acuñado en 1884 por el físico y químico británico Frederick Guthrie (1833-1886). La palabra proviene del griego εὐ - (eû)  'bien' y τῆξῐς (têxis)  'fusión'. ^[2] Antes de sus estudios, los químicos asumían "que la aleación de punto de fusión mínimo debe tener sus constituyentes en algunas proporciones atómicas simples", lo que de hecho se demostró que no era así. ^[5]

La solidificación eutéctica se define de la siguiente manera: ^[6]

${\displaystyle {\text{Líquido}}\quad {\xrightarrow[{\text{enfriamiento}}]{{\text{eutéctico}} \atop {\text{temperatura}}}}\quad \alpha {\text{solución sólida}}\ +\ \beta {\text{solución sólida}}}$

Este tipo de reacción es una reacción invariante, porque está en equilibrio térmico ; otra forma de definir esto es que el cambio en la energía libre de Gibbs es igual a cero. De manera tangible, esto significa que las soluciones líquida y dos sólidas coexisten al mismo tiempo y están en equilibrio químico . También hay un arresto térmico durante la duración del cambio de fase durante el cual la temperatura del sistema no cambia. ^[6]

La macroestructura sólida resultante de una reacción eutéctica depende de algunos factores, siendo el más importante la forma en que se nuclean y crecen las dos soluciones sólidas. La estructura más común es la estructura laminar , pero otras estructuras posibles incluyen la estructura en forma de varilla, la estructura globular y la estructura acicular . ^[7]

Las composiciones de los sistemas eutécticos que no están en el punto eutéctico se pueden clasificar como hipoeutécticas o hipereutécticas :

• Las composiciones hipoeutécticas son aquellas con una mayor composición de especies α y una menor composición porcentual de especies β que la composición eutéctica (E)

• Las composiciones hipereutécticas se caracterizan como aquellas con una mayor composición de especies β y una menor composición de especies α que la composición eutéctica.

A medida que se reduce la temperatura de una composición no eutéctica, la mezcla líquida precipitará un componente de la mezcla antes que el otro. En una solución hipereutéctica, habrá una fase proeutectoide de la especie β, mientras que una solución hipoeutéctica tendrá una fase proeutéctica α. ^[6]

Las aleaciones eutécticas tienen dos o más materiales y tienen una composición eutéctica. Cuando una aleación no eutéctica se solidifica, sus componentes se solidifican a diferentes temperaturas, exhibiendo un rango de fusión plástico. Por el contrario, cuando una aleación eutéctica bien mezclada se funde, lo hace a una única temperatura precisa. Las diversas transformaciones de fase que ocurren durante la solidificación de una composición de aleación particular se pueden entender trazando una línea vertical desde la fase líquida a la fase sólida en el diagrama de fases de esa aleación.

Algunos usos de las aleaciones eutécticas incluyen:

• Relés de sobrecarga de aleación eutéctica NEMA para protección eléctrica de motores trifásicos para bombas, ventiladores, transportadores y otros equipos de proceso de fábrica. ^[8]
• Aleaciones eutécticas para soldadura , tanto las aleaciones tradicionales compuestas de plomo (Pb) y estaño (Sn), a veces con plata (Ag) u oro (Au) adicionales —especialmente las aleaciones Sn ₆₃ Pb ₃₇ y Sn ₆₂ Pb ₃₆ Ag ₂ para electrónica— como las aleaciones de soldadura sin plomo más nuevas, en particular las compuestas de estaño (Sn), plata (Ag) y cobre (Cu), como Sn _96.5 Ag _3.5 .
• Aleaciones de fundición, como aluminio-silicio y hierro fundido (con una composición de 4,3% de carbono en el hierro que produce un eutéctico austenita - cementita )
• Los chips de silicio se unen eutécticamente a sustratos revestidos de oro a través de un eutéctico de silicio-oro mediante la aplicación de energía ultrasónica al chip.
• Soldadura fuerte , donde la difusión puede eliminar elementos de aleación de la unión, de modo que la fusión eutéctica solo es posible al principio del proceso de soldadura fuerte
• Respuesta de temperatura, por ejemplo, metal de Wood y metal de Field para rociadores contra incendios
• Reemplazos de mercurio no tóxicos , como el galinstan
• Metales vítreos experimentales , con resistencia extremadamente alta y resistencia a la corrosión .
• Aleaciones eutécticas de sodio y potasio ( NaK ) que son líquidas a temperatura ambiente y se utilizan como refrigerante en reactores nucleares experimentales de neutrones rápidos .

• El cloruro de sodio y el agua forman una mezcla eutéctica cuyo punto eutéctico es -21,2 °C ^[9] y 23,3% de sal en masa. ^[10] La naturaleza eutéctica de la sal y el agua se aprovecha cuando la sal se esparce en las carreteras para facilitar la remoción de nieve o se mezcla con hielo para producir bajas temperaturas (por ejemplo, en la elaboración tradicional de helados ).
• La combinación etanol-agua tiene un punto eutéctico inusualmente sesgado, es decir, está cerca del etanol puro, lo que establece el punto máximo obtenible mediante congelación fraccionada .
• La "sal solar", 60% NaNO ₃ y 40% KNO ₃ , forma una mezcla de sales fundidas eutécticas que se utiliza para el almacenamiento de energía térmica en plantas de energía solar concentrada . ^[11] Para reducir el punto de fusión eutéctico en las sales fundidas solares, se utiliza nitrato de calcio en la siguiente proporción: 42% Ca(NO ₃ ) ₂ , 43% KNO ₃ y 15% NaNO ₃ .
• La lidocaína y la prilocaína , ambas sólidas a temperatura ambiente, forman un eutéctico, que es un aceite con un punto de fusión de 16 °C (61 °F), que se utiliza en preparaciones de mezcla eutéctica de anestésicos locales (EMLA).
• El mentol y el alcanfor , ambos sólidos a temperatura ambiente, forman un eutéctico que es líquido a temperatura ambiente en las siguientes proporciones: 8:2, 7:3, 6:4 y 5:5. Ambas sustancias son ingredientes comunes en preparaciones extemporáneas de farmacia. ^[12]
• Los minerales pueden formar mezclas eutécticas en rocas ígneas , dando lugar a texturas de intercrecimiento características que exhibe, por ejemplo, la granofira . ^[13]
• Algunas tintas son mezclas eutécticas, lo que permite que las impresoras de inyección de tinta funcionen a temperaturas más bajas. ^[14]
• El cloruro de colina produce mezclas eutécticas con muchos productos naturales como el ácido cítrico , el ácido málico y los azúcares . Estas mezclas líquidas pueden emplearse, por ejemplo, para obtener extractos antioxidantes y antidiabéticos a partir de productos naturales . ^[15]

El mecanismo de fortalecimiento primario de la estructura eutéctica en los metales es el fortalecimiento compuesto (ver mecanismos de fortalecimiento de los materiales ). Este mecanismo de deformación funciona a través de la transferencia de carga entre las dos fases constituyentes, donde la fase más flexible transfiere la tensión a la fase más rígida. ^[16] Al aprovechar la resistencia de la fase rígida y la ductilidad de la fase flexible, aumenta la tenacidad general del material. A medida que la composición varía a formaciones hipoeutécticas o hipereutécticas, el mecanismo de transferencia de carga se vuelve más complejo, ya que existe una transferencia de carga entre la fase eutéctica y la fase secundaria, así como la transferencia de carga dentro de la propia fase eutéctica.

Un segundo mecanismo de fortalecimiento ajustable de las estructuras eutécticas es el espaciamiento de la fase secundaria. Al cambiar el espaciamiento de la fase secundaria, también se modifica la fracción de contacto entre las dos fases a través de los límites de fase compartidos. Al disminuir el espaciamiento de la fase eutéctica, creando una estructura eutéctica fina, se comparte más área de superficie entre las dos fases constituyentes, lo que da como resultado una transferencia de carga más efectiva. ^[17] En la microescala, el área límite adicional actúa como una barrera para las dislocaciones que refuerzan aún más el material. Como resultado de este mecanismo de fortalecimiento, las estructuras eutécticas gruesas tienden a ser menos rígidas pero más dúctiles, mientras que las estructuras eutécticas finas son más rígidas pero más frágiles. ^[17] El espaciamiento de la fase eutéctica se puede controlar durante el procesamiento, ya que está directamente relacionado con la velocidad de enfriamiento durante la solidificación de la estructura eutéctica. Por ejemplo, para una estructura eutéctica laminar simple, el espaciamiento mínimo de las láminas es: ^[18]

${\displaystyle \lambda ^{*}={\frac {2\gamma V_{m}T_{E}}{\Delta H*\Delta T_{0}}}}$

Donde es la energía superficial del límite de dos fases, es el volumen molar de la fase eutéctica,   es la temperatura de solidificación de la fase eutéctica,  es la entalpía de formación de la fase eutéctica y  es el subenfriamiento del material. Por lo tanto, al alterar el subenfriamiento y, por extensión, la velocidad de enfriamiento, se controla el espaciamiento mínimo alcanzable de la fase secundaria.${\estilo de visualización \gamma}$$Estilo de visualización V_ {m}$ $Estilo de visualización T_ {E}}$${\displaystyle \Delta H}$${\displaystyle \Delta T_{0}}$

El fortalecimiento de las fases eutécticas metálicas para resistir la deformación a altas temperaturas (ver deformación por fluencia ) es más complicado ya que el mecanismo de deformación primaria cambia dependiendo del nivel de tensión aplicado. A altas temperaturas donde la deformación está dominada por el movimiento de dislocación, el fortalecimiento de la transferencia de carga y el espaciamiento de la fase secundaria se mantienen ya que continúan resistiendo el movimiento de dislocación. A deformaciones más bajas donde la fluencia de Nabarro-Herring es dominante, la forma y el tamaño de la estructura de la fase eutéctica juegan un papel significativo en la deformación del material ya que afecta el área límite disponible para que ocurra la difusión de vacantes. ^[19]

Cuando la solución por encima del punto de transformación es sólida, en lugar de líquida, puede ocurrir una transformación eutectoide análoga. Por ejemplo, en el sistema hierro-carbono, la fase austenítica puede sufrir una transformación eutectoide para producir ferrita y cementita , a menudo en estructuras lamelares como la perlita y la bainita . Este punto eutectoide ocurre a 723 °C (1333 °F) y 0,76 % en peso de carbono. ^[20]

Una transformación peritectoide es un tipo de reacción isotérmica reversible en la que dos fases sólidas reaccionan entre sí al enfriarse una aleación binaria, ternaria, ..., n -aria para crear una fase sólida completamente diferente y única. ^[21] La reacción juega un papel clave en el orden y la descomposición de las fases cuasicristalinas en varios tipos de aleaciones. ^[22] También se predice una transición estructural similar para los cristales columnares giratorios.

Las transformaciones peritécticas también son similares a las reacciones eutécticas. En ellas, una fase líquida y una sólida de proporciones fijas reaccionan a una temperatura fija para producir una única fase sólida. Dado que el producto sólido se forma en la interfase entre los dos reactivos, puede formar una barrera de difusión y, en general, hace que dichas reacciones se desarrollen mucho más lentamente que las transformaciones eutécticas o eutectoides. Debido a esto, cuando una composición peritéctica se solidifica, no muestra la estructura laminar que se encuentra en la solidificación eutéctica.

Tal transformación existe en el sistema hierro-carbono, como se ve cerca de la esquina superior izquierda de la figura. Se asemeja a una eutéctica invertida, en la que la fase δ se combina con el líquido para producir austenita pura a 1495 °C (2723 °F) y 0,17 % de carbono.

A la temperatura de descomposición peritéctica, el compuesto, en lugar de fundirse, se descompone en otro compuesto sólido y en un líquido. La proporción de cada uno de ellos se determina mediante la regla de la palanca . En el diagrama de fases Al-Au , por ejemplo, se puede ver que sólo dos de las fases se funden de forma congruente, AuAl ₂ y Au ₂ Al , mientras que el resto se descomponen de forma peritéctica.

No todos los sistemas de punto de fusión mínimo son "eutécticos". La alternativa de "solución sólida pobre" se puede ilustrar comparando los sistemas comunes de metales preciosos Cu-Ag y Cu-Au. Cu-Ag, fuente por ejemplo https://himikatus.ru/art/phase-diagr1/Ag-Cu.php, es un verdadero sistema eutéctico. El punto de fusión eutéctico está a 780 C, con límites de solubilidad sólida a finuras de 80 y 912 en peso, y eutéctico a 719. Dado que Cu-Ag es un verdadero eutéctico, cualquier plata con finuras en cualquier lugar entre 80 y 912 alcanzará la línea de solidus, y por lo tanto se fundirá al menos parcialmente, exactamente a 780 C. La aleación eutéctica con finura exactamente 719 alcanzará la línea de liquidus, y por lo tanto se fundirá por completo, a esa temperatura exacta sin ningún aumento adicional de temperatura hasta que toda la aleación se haya fundido. Cualquier plata con una finura entre 80 y 912 pero no exactamente 719 también alcanzará la línea de solidus exactamente a 780 C, pero se fundirá parcialmente. Dejará un residuo sólido con una finura de exactamente 912 o exactamente 80, pero nunca algo de ambas. Se fundirá a temperatura constante sin un mayor aumento de temperatura hasta que la cantidad exacta de aleación eutéctica (finura 719) se haya fundido para dividir la aleación en fusión eutéctica y residuo de solución sólida. Al calentar más, el residuo de solución sólida se disuelve en la fusión y cambia su composición hasta que se alcanza la línea de liquidus y todo el residuo se ha disuelto. La fuente de Cu-Au, por ejemplo https://himikatus.ru/art/phase-diagr1/Au-Cu.php muestra un punto de fusión mínimo a 910 C y se da como 44 % atómico de Cu, que se convierte en aproximadamente 20 por ciento en peso de Cu, aproximadamente 800 de finura de oro. Pero esto no es un verdadero eutéctico. El oro de 800 grados se funde a 910 C, formando una masa fundida de exactamente la misma composición, y toda la aleación se fundirá exactamente a la misma temperatura. Pero las diferencias ocurren fuera de la composición mínima. A diferencia de la plata con una finura distinta de 719 (que se funde parcialmente exactamente a 780 C a través de un amplio rango de finuras), el oro con una finura distinta de 800 alcanzará el estado sólido y comenzará a fundirse parcialmente a una temperatura diferente y superior a 910 C, dependiendo de la finura de la aleación. La fusión parcial provoca algunos cambios en la composición: el líquido tendrá una finura más cercana a 800 que el sólido restante, pero el líquido no tendrá una finura de exactamente 800 y la finura del sólido restante dependerá de la finura del líquido. La razón subyacente es que para un sistema eutéctico como Cu-Ag, la solubilidad en fase líquida es buena, pero la solubilidad en fase sólida es limitada. Por lo tanto, cuando una aleación de plata y cobre se congela, en realidad se separa en cristales de plata de finura 912 y plata de finura 80, ambos están saturados y siempre tienen la misma composición en el punto de congelación de 780 C. Por lo tanto, la aleación justo por debajo de 780 C consta de dos tipos de cristales de exactamente la misma composición, independientemente de la composición total de la aleación, solo difiere la cantidad relativa de cada tipo de cristales.Por lo tanto, siempre se funden a 780 C hasta que se agoten uno u otro tipo de cristales, o ambos. Por el contrario, en el sistema Cu-Au los componentes son miscibles en el punto de fusión en todas las composiciones, incluso en estado sólido. Puede haber cristales de cualquier composición, que se fundirán a diferentes temperaturas según la composición. Sin embargo, el sistema Cu-Au es una solución sólida "pobre". Existe un desajuste sustancial entre los átomos en el sólido que, sin embargo, cerca del punto de fusión se supera por la entropía del movimiento térmico que mezcla los átomos. Sin embargo, ese desajuste desfavorece a la solución Cu-Au en relación con las fases en las que los átomos están mejor ajustados, como el fundido, y hace que el punto de fusión caiga por debajo del punto de fusión de los componentes.

La composición y la temperatura de un eutéctico se pueden calcular a partir de la entalpía y la entropía de fusión de cada componente. ^[23]

La energía libre de Gibbs G depende de su propio diferencial:

${\displaystyle G=H-TS\Rightarrow {\begin{cases}H=G+TS\\\left({\frac {\partial G}{\partial T}}\right)_{P}=-S\end{cases}}\Rightarrow H=GT\left({\frac {\partial G}{\partial T}}\right)_{P}.}$

Así, la derivada G / T a presión constante se calcula mediante la siguiente ecuación:

${\displaystyle \left({\frac {\parcial G/T}{\parcial T}}\right)_{P}={\frac {1}{T}}\left({\frac {\parcial G}{\parcial T}}\right)_{P}-{\frac {1}{T^{2}}}G=-{\frac {1}{T^{2}}}\left(GT\left({\frac {\parcial G}{\parcial T}}\right)_{P}\right)=-{\frac {H}{T^{2}}}.}$

El potencial químico se calcula si suponemos que la actividad es igual a la concentración:${\displaystyle \mu_{i}}$

${\displaystyle \mu_{i}=\mu_{i}^{\circ}+RT\ln {\frac {a_{i}}{a}}\approx \mu_{i}^{\circ}+RT\ln x_{i}.}$

En el equilibrio, , se obtiene así${\displaystyle \mu_{i}=0}$${\displaystyle \mu_{i}^{\circ}}$

${\displaystyle \mu_{i}=\mu_{i}^{\circ}+RT\ln x_{i}=0\Rightarrow \mu_{i}^{\circ}=-RT\ln x_{i}.}$

Usando ^{[ aclaración necesaria ]} e integrando obtenemos

${\displaystyle \left({\frac {\parcial \mu _{i}/T}{\parcial T}}\right)_{P}={\frac {\parcial }{\parcial T}}\left(R\ln x_{i}\right)\Rightarrow R\ln x_{i}=-{\frac {H_{i}^{\circ }}{T}}+K.}$

La constante de integración K se puede determinar para un componente puro con una temperatura de fusión y una entalpía de fusión :${\displaystyle T^{\circ}}$${\displaystyle H^{\circ}}$

${\displaystyle x_{i}=1\Rightarrow T=T_{i}^{\circ }\Rightarrow K={\frac {H_{i}^{\circ }}{T_{i}^{\circ }}}.}$

Obtenemos una relación que determina la fracción molar en función de la temperatura para cada componente:

${\displaystyle R\ln x_{i}=-{\frac {H_{i}^{\circ }}{T}}+{\frac {H_{i}^{\circ }}{T_{i}^{\circ }}}.}$

La mezcla de n componentes se describe mediante el sistema

${\displaystyle {\begin{cases}\ln x_{i}+{\frac {H_{i}^{\circ }}{RT}}-{\frac {H_{i}^{\circ }}{RT_{i}^{\circ }}}=0,\\\suma \limits _{i=1}^{n}x_{i}=1.\end{cases}}}$

${\displaystyle {\begin{cases}\forall i<n\Rightarrow \ln x_{i}+{\frac {H_{i}^{\circ }}{RT}}-{\frac {H_{i}^{\circ }}{RT_{i}^{\circ }}}=0,\\\ln \left(1-\sum \limits _{i=1}^{n-1}x_{i}\right)+{\frac {H_{n}^{\circ }}{RT}}-{\frac {H_{n}^{\circ }}{RT_{n}^{\circ }}}=0,\end{cases}}}$

que se puede resolver mediante

${\displaystyle {\begin{array}{c}\left[{\begin{array}{*{20}c}{\Delta x_{1}}\\{\Delta x_{2}}\\{\Delta x_{3}}\\\vdots \\{\Delta x_{n-1}}\\{\Delta T}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{1/x_{1}}&0&0&0&0&{-{\frac {H_{1}^{\circ }}{RT^{2}}}}\\0&{1/x_{2}}&0&0&0&{-{\frac {H_{2}^{\circ }}{RT^{2}}}}\\0&0&{1/x_{3}}&0&0&{-{\frac {H_{3}^{\circ }}{RT^{2}}}}\\\vdots &\ddots &\ddots &\ddots &\ddots &{\vdots }\\0&0&0&0&{1/x_{n-1}}&{-{\frac {H_{n-1}^{\circ }}{RT^{2}}}}\\{\frac {-1}{1-\sum \limits _{i=1}^{n-1}{x_{i}}}}&{\frac {-1}{1-\sum \limits _{i=1}^{n-1}{x_{i}}}}&{\frac {-1}{1-\sum \limits _{i=1}^{n-1}{x_{i}}}}&{\frac {-1}{1-\sum \limits _{i=1}^{n-1}{x_{i}}}}&{\frac {-1}{1-\sum \limits _{i=1}^{n-1}{x_{i}}}}&{-{\frac {H_{n}^{\circ }}{RT^{2}}}}\\\end{array}}\right]^{-1}.\left[{\begin{array}{*{20}c}{\ln x_{1}+{\frac {H_{1}^{\circ }}{RT}}-{\frac {H_{1}^{\circ }}{RT_{1}^{\circ }}}}\\{\ln x_{2}+{\frac {H_{2}^{\circ }}{RT}}-{\frac {H_{2}^{\circ }}{RT_{2}^{\circ }}}}\\{\ln x_{3}+{\frac {H_{3}^{\circ }}{RT}}-{\frac {H_{3}^{\circ }}{RT_{3}^{\circ }}}}\\\vdots \\{\ln x_{n-1}+{\frac {H_{n-1}^{\circ }}{RT}}-{\frac {H_{n-1}^{\circ }}{RT_{n-1}^{\circ }}}}\\{\ln \left({1-\sum \limits _{i=1}^{n-1}{x_{i}}}\right)+{\frac {H_{n}^{\circ }}{RT}}-{\frac {H_{n}^{\circ }}{RT_{n}^{\circ }}}}\\\end{array}}\right]\end{array}}}$

• Azeotropo o mezcla de ebullición constante
• Depresión del punto de congelación
• Aleación de bajo punto de fusión

• Smith, William F.; Hashemi, Javad (2006), Fundamentos de la ciencia y la ingeniería de materiales (4.ª ed.), McGraw-Hill, ISBN 978-0-07-295358-9.

Busque eutéctico en Wikcionario, el diccionario libre.

• Askeland, Donald R.; Pradeep P. Phule (2005). La ciencia y la ingeniería de los materiales . Thomson-Engineering. ISBN 978-0-534-55396-8.
• Easterling, Edward (1992). Transformaciones de fase en metales y aleaciones . CRC. ISBN 978-0-7487-5741-1.
• Mortimer, Robert G. (2000). Química física . Academic Press. ISBN 978-0-12-508345-4.
• Reed-Hill, RE; Reza Abbaschian (1992). Principios de metalurgia física . Thomson-Engineering. ISBN 978-0-534-92173-6.
• Sadoway, Donald (2004). "Equilibrios de fases y diagramas de fases" (PDF) . 3.091 Introducción a la química del estado sólido, otoño de 2004 . MIT Open Courseware. Archivado desde el original (PDF) el 20 de octubre de 2005 . Consultado el 12 de abril de 2006 .