Bloqueo de mareas
El bloqueo de marea entre un par de cuerpos astronómicos que orbitan juntos ocurre cuando uno de los objetos alcanza un estado en el que ya no hay ningún cambio neto en su tasa de rotación a lo largo de una órbita completa. En el caso en que un cuerpo bloqueado por marea posee rotación sincrónica, el objeto tarda tanto en girar sobre su propio eje como en girar alrededor de su compañero. Por ejemplo, el mismo lado de la Luna siempre está de cara a la Tierra , aunque hay cierta variabilidad porque la órbita de la Luna no es perfectamente circular. Por lo general, solo el satélite está bloqueado por marea con el cuerpo más grande. [1] Sin embargo, si tanto la diferencia de masa entre los dos cuerpos como la distancia entre ellos son relativamente pequeñas, cada uno puede estar bloqueado por marea con el otro; este es el caso de Plutón y Caronte , así como de Eris y Dysnomia . Los nombres alternativos para el proceso de bloqueo de marea son bloqueo gravitacional , [2] rotación capturada y bloqueo de espín-órbita .
El efecto surge entre dos cuerpos cuando su interacción gravitatoria ralentiza la rotación de un cuerpo hasta que se bloquea por marea. A lo largo de muchos millones de años, la interacción fuerza cambios en sus órbitas y velocidades de rotación como resultado del intercambio de energía y la disipación de calor . Cuando uno de los cuerpos alcanza un estado en el que ya no hay ningún cambio neto en su velocidad de rotación a lo largo de una órbita completa, se dice que está bloqueado por marea. [3] El objeto tiende a permanecer en este estado porque salir de él requeriría agregar energía nuevamente al sistema. La órbita del objeto puede migrar con el tiempo para deshacer el bloqueo de marea, por ejemplo, si un planeta gigante perturba el objeto.
Existe una ambigüedad en el uso de los términos "bloqueo de marea" y "bloqueo de marea", ya que algunas fuentes científicas lo usan para referirse exclusivamente a la rotación sincrónica 1:1 (por ejemplo, la Luna), mientras que otras incluyen resonancias orbitales no sincrónicas en las que no hay más transferencia de momento angular en el curso de una órbita (por ejemplo, Mercurio). [4] En el caso de Mercurio , el planeta completa tres rotaciones por cada dos revoluciones alrededor del Sol, una resonancia de giro-órbita de 3:2. En el caso especial donde una órbita es casi circular y el eje de rotación del cuerpo no está significativamente inclinado, como la Luna, el bloqueo de marea da como resultado que el mismo hemisferio del objeto giratorio esté constantemente de frente a su compañero. [3] [4] [5] Independientemente de la definición de bloqueo de marea que se use, el hemisferio que es visible cambia ligeramente debido a las variaciones en la velocidad orbital del cuerpo bloqueado y la inclinación de su eje de rotación a lo largo del tiempo.
Mecanismo

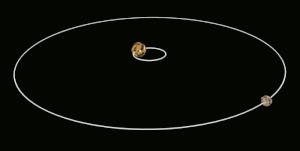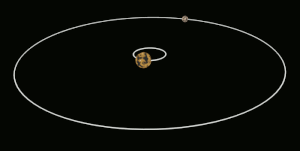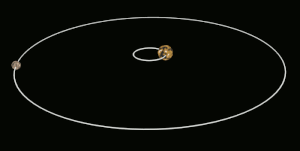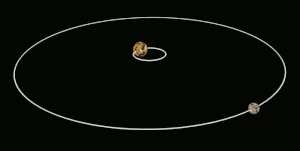
Consideremos un par de objetos que orbitan conjuntamente, A y B. El cambio en la tasa de rotación necesario para bloquear por marea el cuerpo B con el cuerpo más grande A es causado por el torque aplicado por la gravedad de A sobre las protuberancias que ha inducido en B por las fuerzas de marea . [6]
La fuerza gravitatoria del objeto A sobre B variará con la distancia, siendo mayor en la superficie más cercana a A y menor en la más distante. Esto crea un gradiente gravitacional a través del objeto B que distorsionará ligeramente su forma de equilibrio . El cuerpo del objeto B se alargará a lo largo del eje orientado hacia A y, a la inversa, se reducirá ligeramente en dimensión en direcciones ortogonales a este eje. Las distorsiones alargadas se conocen como abultamientos de marea . (Para la Tierra sólida, estos abultamientos pueden alcanzar desplazamientos de hasta alrededor de 0,4 m o 1 pie 4 pulgadas [7] ) Cuando B aún no está bloqueado por mareas, los abultamientos se desplazan sobre su superficie debido a los movimientos orbitales, y uno de los dos abultamientos de marea "altos" se desplaza cerca del punto donde el cuerpo A está por encima. Para los grandes cuerpos astronómicos que son casi esféricos debido a la autogravitación, la distorsión de marea produce un esferoide ligeramente alargado , es decir, un elipsoide axialmente simétrico que se alarga a lo largo de su eje mayor. Los cuerpos más pequeños también experimentan distorsión, pero esta distorsión es menos regular.
El material de B ejerce resistencia a esta remodelación periódica causada por la fuerza de marea. En efecto, se requiere algún tiempo para remodelar B a la forma de equilibrio gravitacional, momento en el cual las protuberancias que se están formando ya se han alejado a cierta distancia del eje A-B por la rotación de B. Vistos desde un punto de observación en el espacio, los puntos de máxima extensión de las protuberancias están desplazados del eje orientado hacia A. Si el período de rotación de B es más corto que su período orbital, las protuberancias se desplazan hacia delante del eje orientado hacia A en la dirección de rotación, mientras que si el período de rotación de B es más largo, las protuberancias se quedan atrás.
Como los abultamientos están desplazados del eje A-B, la atracción gravitatoria de A sobre la masa que se encuentra en ellos ejerce un par de torsión sobre B. El par de torsión en el abultamiento que mira hacia A actúa para alinear la rotación de B con su período orbital, mientras que el abultamiento "posterior", que mira en dirección opuesta a A, actúa en sentido opuesto. Sin embargo, el abultamiento del lado que mira hacia A está más cerca de A que el abultamiento posterior por una distancia de aproximadamente el diámetro de B, y por lo tanto experimenta una fuerza gravitatoria y un par de torsión ligeramente más fuertes. El par de torsión resultante neto de ambos abultamientos, entonces, siempre está en la dirección que actúa para sincronizar la rotación de B con su período orbital, lo que finalmente conduce al bloqueo de marea.
Cambios orbitales

En (2), con la rotación invertida, la fuerza neta se opone a la dirección de la órbita del satélite, bajándolo (desaceleración de marea).

En este proceso se conserva el momento angular de todo el sistema A–B, de modo que cuando B se desacelera y pierde momento angular rotacional, su momento angular orbital aumenta en una cantidad similar (también hay algunos efectos menores en la rotación de A). Esto da como resultado una elevación de la órbita de B alrededor de A en tándem con su desaceleración rotacional. En el otro caso en el que B comienza a rotar demasiado lentamente, el bloqueo de marea acelera su rotación y reduce su órbita.
Bloqueo del cuerpo mayor
El efecto de bloqueo de marea también lo experimenta el cuerpo más grande A, pero a un ritmo más lento porque el efecto gravitacional de B es más débil debido a la menor masa de B. Por ejemplo, la rotación de la Tierra se está ralentizando gradualmente por la Luna, en una cantidad que se hace notoria con el tiempo geológico como lo revela el registro fósil. [8] Las estimaciones actuales son que esto (junto con la influencia de las mareas del Sol) ha ayudado a alargar el día terrestre de aproximadamente 6 horas a las 24 horas actuales (a lo largo de aproximadamente 4.500 millones de años). Actualmente, los relojes atómicos muestran que el día de la Tierra se alarga, en promedio, unos 2,3 milisegundos por siglo. [9] Si se le da suficiente tiempo, esto crearía un bloqueo de marea mutuo entre la Tierra y la Luna. La duración del día de la Tierra aumentaría y la duración de un mes lunar también aumentaría. El día sideral de la Tierra eventualmente tendría la misma duración que el período orbital de la Luna , aproximadamente 47 veces la duración del día de la Tierra en la actualidad. Sin embargo, no se espera que la Tierra quede bloqueada por mareas con la Luna antes de que el Sol se convierta en un gigante rojo y envuelva a la Tierra y la Luna. [10] [11]
En el caso de cuerpos de tamaño similar, el efecto puede ser de magnitud comparable para ambos, y ambos pueden quedar bloqueados por mareas entre sí en una escala de tiempo mucho más corta. Un ejemplo es el planeta enano Plutón y su satélite Caronte . Ya han alcanzado un estado en el que Caronte es visible desde un solo hemisferio de Plutón y viceversa. [12]
Órbitas excéntricas
Un error muy extendido es creer que un cuerpo bloqueado por las mareas gira permanentemente un lado hacia su anfitrión.
— Heller y otros (2011) [4]
En el caso de órbitas que no tienen una excentricidad cercana a cero, la velocidad de rotación tiende a bloquearse con la velocidad orbital cuando el cuerpo está en el periapsis , que es el punto de interacción de marea más fuerte entre los dos objetos. Si el objeto en órbita tiene un compañero, este tercer cuerpo puede hacer que la velocidad de rotación del objeto principal varíe de manera oscilatoria. Esta interacción también puede impulsar un aumento en la excentricidad orbital del objeto en órbita alrededor del primario, un efecto conocido como bombeo de excentricidad. [13]
En algunos casos en los que la órbita es excéntrica y el efecto de marea es relativamente débil, el cuerpo más pequeño puede terminar en una llamada resonancia de giro-órbita , en lugar de estar bloqueado por marea. Aquí, la relación entre el período de rotación de un cuerpo y su propio período orbital es una fracción simple diferente de 1:1. Un caso bien conocido es la rotación de Mercurio , que está bloqueado en su propia órbita alrededor del Sol en una resonancia de 3:2. [2] Esto da como resultado que la velocidad de rotación coincida aproximadamente con la velocidad orbital alrededor del perihelio. [14]
Se espera que muchos exoplanetas (especialmente los cercanos) se encuentren en resonancias de giro-órbita superiores a 1:1. Un planeta terrestre similar a Mercurio, por ejemplo, puede quedar atrapado en una resonancia de giro-órbita de 3:2, 2:1 o 5:2, y la probabilidad de cada una de ellas depende de la excentricidad orbital. [15]
Aparición
Lunas

Las veinte lunas conocidas del Sistema Solar que son lo suficientemente grandes como para ser redondas están sincronizadas con sus lunas primarias, porque orbitan muy cerca y la fuerza de marea aumenta rápidamente (como una función cúbica ) al disminuir la distancia. [16] Por otro lado, la mayoría de los satélites exteriores irregulares de los planetas gigantes (por ejemplo, Febe ), que orbitan mucho más lejos que las grandes lunas conocidas, no están sincronizados con las mareas. [ cita requerida ]
Plutón y Caronte son un ejemplo extremo de un bloqueo de marea. Caronte es una luna relativamente grande en comparación con su luna principal y también tiene una órbita muy cercana . Esto da como resultado que Plutón y Caronte estén mutuamente bloqueados por marea. Las otras lunas de Plutón no están bloqueadas por marea; Styx , Nix , Kerberos e Hydra giran caóticamente debido a la influencia de Caronte. [17] De manera similar, Eris y Dysnomia están mutuamente bloqueadas por marea. [18] Orcus y Vanth también podrían estar mutuamente bloqueados por marea, pero los datos no son concluyentes. [19]
La situación del bloqueo de mareas en las lunas de asteroides es en gran parte desconocida, pero se espera que los sistemas binarios que orbitan cerca estén bloqueados por mareas, [ cita requerida ] así como los sistemas binarios de contacto .
La luna de la Tierra

La rotación y los períodos orbitales de la Luna están sincronizados entre sí por las mareas, por lo que, independientemente de cuándo se observe la Luna desde la Tierra, siempre se verá el mismo hemisferio de la Luna. La mayor parte del lado oculto de la Luna no se vio hasta 1959, cuando se transmitieron fotografías de la mayor parte del lado oculto desde la nave espacial soviética Luna 3. [ 20]
Cuando se observa la Tierra desde la Luna, no parece moverse por el cielo, sino que permanece en el mismo lugar y muestra casi toda su superficie a medida que gira sobre su eje. [21]
A pesar de que los períodos de rotación y órbita de la Luna están exactamente sincronizados, alrededor del 59 por ciento de la superficie total de la Luna puede verse con observaciones repetidas desde la Tierra, debido a los fenómenos de libración y paralaje . Las libraciones son causadas principalmente por la velocidad orbital variable de la Luna debido a la excentricidad de su órbita: esto permite que se puedan ver hasta aproximadamente 6° más a lo largo de su perímetro desde la Tierra. El paralaje es un efecto geométrico: en la superficie de la Tierra, los observadores están desplazados de la línea que pasa por los centros de la Tierra y la Luna; esto explica una diferencia de aproximadamente 1° en la superficie de la Luna que puede verse alrededor de los lados de la Luna al comparar las observaciones realizadas durante la salida y la puesta de la luna. [22]
Planetas
Durante algún tiempo se creyó que Mercurio se encontraba en rotación sincrónica con el Sol. Esto se debía a que, siempre que Mercurio se encontraba en la mejor posición para la observación, el mismo lado miraba hacia adentro. Las observaciones de radar realizadas en 1965 demostraron, en cambio, que Mercurio tiene una resonancia de giro-órbita de 3:2, rotando tres veces por cada dos revoluciones alrededor del Sol, lo que da como resultado la misma posición en esos puntos de observación. Los modelos han demostrado que Mercurio fue capturado en el estado de giro-órbita de 3:2 muy temprano en su historia, probablemente entre 10 y 20 millones de años después de su formación. [23]
El intervalo de 583,92 días entre los sucesivos acercamientos de Venus a la Tierra equivale a 5,001444 días solares venusianos, lo que hace que sea aproximadamente la misma cara visible desde la Tierra en cada acercamiento. Se desconoce si esta relación surgió por casualidad o es el resultado de algún tipo de bloqueo de marea con la Tierra. [24]
El exoplaneta Proxima Centauri b descubierto en 2016, que orbita alrededor de Proxima Centauri , está casi con certeza bloqueado por mareas, expresando una rotación sincronizada o una resonancia de giro-órbita de 3:2 como la de Mercurio. [25]
Una forma hipotética de exoplanetas bloqueados por mareas son los planetas globo ocular , que a su vez se dividen en planetas globo ocular "calientes" y "fríos". [26] [27]
Estrellas
Se espera que las estrellas binarias cercanas en todo el universo estén unidas por mareas entre sí, y se cree que los planetas extrasolares que se ha descubierto que orbitan sus estrellas primarias extremadamente cerca también están unidos por mareas a ellas. Un ejemplo inusual, confirmado por MOST , puede ser Tau Boötis , una estrella que probablemente esté unida por mareas a su planeta Tau Boötis b . [28] Si es así, el bloqueo por mareas es casi con certeza mutuo. [29] [30]
Escala de tiempo
Se puede obtener una estimación del tiempo que tarda un cuerpo en quedar atrapado por las mareas utilizando la siguiente fórmula: [31]
dónde
- es la velocidad de giro inicial expresada en radianes por segundo ,
- es el semieje mayor del movimiento del satélite alrededor del planeta (dado por el promedio de las distancias de periapsis y apoapsis ),
- es el momento de inercia del satélite, donde es la masa del satélite y es el radio medio del satélite,
- es la función de disipación del satélite,
- es la constante gravitacional ,
- es la masa del planeta (es decir, el objeto en órbita), y
- es el número de marea de Love del satélite.
y son generalmente muy poco conocidos, excepto por la Luna, que tiene . Para una estimación realmente aproximada, es común tomar (quizás de manera conservadora, dando tiempos de bloqueo sobreestimados), y
dónde
- es la densidad del satélite
- ¿Es la gravedad superficial del satélite?
- es la rigidez del satélite. Esto puede tomarse aproximadamente como 3 × 1010 N/m 2 para objetos rocosos y 4 × 109 N/m2 para los helados.
Incluso conociendo el tamaño y la densidad del satélite quedan muchos parámetros que deben estimarse (especialmente ω , Q y μ ), por lo que se espera que los tiempos de bloqueo calculados que se obtengan sean inexactos, incluso en factores de diez. Además, durante la fase de bloqueo de marea, el semieje mayor puede haber sido significativamente diferente del observado actualmente debido a la aceleración de marea posterior , y el tiempo de bloqueo es extremadamente sensible a este valor.
Como la incertidumbre es tan alta, las fórmulas anteriores se pueden simplificar para dar una fórmula algo menos engorrosa. Suponiendo que el satélite es esférico, y es sensato suponer una revolución cada 12 horas en el estado inicial no bloqueado (la mayoría de los asteroides tienen períodos de rotación de entre aproximadamente 2 horas y aproximadamente 2 días).
- [32]
con masas en kilogramos, distancias en metros y en newtons por metro cuadrado; puede tomarse aproximadamente como 3 × 1010 N/m 2 para objetos rocosos y 4 × 109 N/m2 para los helados.
Existe una dependencia extremadamente fuerte del semieje mayor .
Para bloquear un cuerpo primario a su satélite, como en el caso de Plutón, los parámetros del satélite y del cuerpo primario se pueden intercambiar.
Una conclusión es que, en igualdad de condiciones (como y ), una luna grande se bloqueará más rápido que una luna más pequeña a la misma distancia orbital del planeta porque crece como el cubo del radio del satélite . Un posible ejemplo de esto es en el sistema de Saturno, donde Hyperion no está bloqueado por mareas, mientras que el más grande Iapetus , que orbita a una distancia mayor, sí lo está. Sin embargo, esto no es claro porque Hyperion también experimenta un fuerte impulso del cercano Titán , que obliga a que su rotación sea caótica.
Las fórmulas anteriores para la escala de tiempo de bloqueo pueden estar desfasadas en órdenes de magnitud, porque ignoran la dependencia de la frecuencia de . Más importante aún, pueden ser inaplicables a sistemas binarios viscosos (estrellas dobles o asteroides dobles que son escombros), porque la dinámica de giro-órbita de dichos cuerpos se define principalmente por su viscosidad, no por su rigidez. [33]
Lista de cuerpos bloqueados por mareas conocidos
Sistema solar
Todos los cuerpos que se muestran a continuación están bloqueados por las mareas y, además, todos ellos, excepto Mercurio, están en rotación sincrónica. (Mercurio está bloqueado por las mareas, pero no en rotación sincrónica).
| Cuerpo padre | Satélites bloqueados por mareas [34] |
|---|---|
| Sol | Mercurio [35] [36] [23] (resonancia de giro-órbita 3:2) |
| Tierra | Luna [37] |
| Marte | Fobos [38] · Deimos [39] |
| Júpiter | Metis [40] · Adrastea · Amaltea [40] · Tebe [40] · Io · Europa · Ganímedes · Calisto |
| Saturno | Pan · Atlas · Prometeo · Pandora · Epimeteo · Jano · Mimas · Encélado [41] · Telesto · Tetis [41] · Calipso · Dione [41] · Rea [41] · Titán · Jápeto [41] |
| Urano | Miranda · Ariel · Umbriel · Titania · Oberón [42] |
| Neptuno | Proteo [43] · Tritón [38] |
| Plutón | Caronte (mutuamente bloqueado) [12] |
| Eris | Disnomia (mutuamente bloqueados) [18] |
Extrasolar
- Los métodos de detección de exoplanetas más exitosos (tránsitos y velocidades radiales) sufren de un claro sesgo observacional que favorece la detección de planetas cercanos a la estrella; así, el 85% de los exoplanetas detectados están dentro de la zona de bloqueo de marea, lo que dificulta estimar la verdadera incidencia de este fenómeno. [44] Se sabe que Tau Boötis está bloqueado por el planeta gigante Tau Boötis b que orbita cerca de ella . [28]
Cadáveres que probablemente serán encerrados
Sistema solar
Basándose en la comparación entre el tiempo probable necesario para que un cuerpo se acople a su órbita primaria y el tiempo que lleva en su órbita actual (comparable con la edad del Sistema Solar para la mayoría de las lunas planetarias), se cree que varias lunas están acopladas. Sin embargo, sus rotaciones no se conocen o no se conocen lo suficiente. Estas son:
Probablemente bloqueado por Saturno
Probablemente bloqueado por Urano
Probablemente bloqueado en Neptuno
Probablemente bloqueados mutuamente por las mareas
Extrasolar
- Gliese 581c , [46] Gliese 581g , [47] [48] Gliese 581b , [49] y Gliese 581e [50] pueden estar bloqueados por marea con su estrella madre Gliese 581. Es casi seguro que Gliese 581d esté capturado en la resonancia de giro-órbita 2:1 o 3:2 con la misma estrella. [51]
- Es probable que todos los planetas del sistema TRAPPIST-1 estén bloqueados por mareas. [52] [53]
Véase también
- Conservación del momento angular : magnitud física conservada; análogo rotacional del momento linealPages displaying short descriptions of redirect targets
- Marea terrestre#Efectos
- Estabilización por gradiente de gravedad : método para la estabilización y orientación de diversas naves espaciales
- Mecanismo de Kozai : fenómeno dinámico que afecta la órbita de un sistema binario perturbado por un tercer cuerpo distante
- Resonancia orbital : influencia gravitacional mutua regular y periódica de cuerpos en órbita
- Habitabilidad planetaria : grado conocido en el que un planeta es adecuado para la vida.
- Rotación pseudosincrónica : una sincronización casi total de la revolución y la rotación en el periastrón
- Límite de Roche : radio orbital en el que un satélite podría desintegrarse debido a la fuerza gravitacional
- Órbita sincrónica : Órbita de un cuerpo astronómico igual al período de rotación promedio de ese cuerpo.
- Aceleración de las mareas : fenómeno natural por el cual se produce el bloqueo de las mareas.
- Rotación alrededor de un eje fijo – Tipo de movimiento
Referencias
- ^ "¿Cuándo se acoplará la Tierra a la Luna?". Universe Today . 12 de abril de 2016. Archivado desde el original el 23 de septiembre de 2016. Consultado el 2 de enero de 2017 .
- ^ ab Clouse, Christopher; et al. (mayo de 2022), "Bloqueo gravitacional de espín-órbita: un enfoque potencial eficaz", European Journal of Physics , 43 (3): 13, arXiv : 2203.09297 , Bibcode :2022EJPh...43c5602C, doi :10.1088/1361-6404/ac5638, S2CID 246962304, 035602
- ^ ab Barnes, Rory, ed. (2010). Formación y evolución de exoplanetas. John Wiley & Sons. pág. 248. ISBN 978-3527408962Archivado desde el original el 6 de agosto de 2023. Consultado el 16 de agosto de 2016 .
- ^ abc Heller, R.; Leconte, J.; Barnes, R. (abril de 2011). "Evolución de la oblicuidad de marea de planetas potencialmente habitables". Astronomía y astrofísica . 528 : 16. arXiv : 1101.2156 . Bibcode :2011A&A...528A..27H. doi :10.1051/0004-6361/201015809. S2CID 118784209. A27.
- ^ Mahoney, TJ (2013). Mercurio. Springer Science & Business Media. ISBN 978-1461479512Archivado desde el original el 6 de agosto de 2023. Consultado el 20 de abril de 2018 .
- ^ Lewis, John (2012). Física y química del sistema solar. Academic Press. pp. 242–243. ISBN 978-0323145848Archivado desde el original el 6 de agosto de 2023. Consultado el 22 de febrero de 2018 .
- ^ Watson, C.; et al. (abril de 2006). "Impacto de los modelos de mareas de la Tierra sólida en las coordenadas GPS y las series temporales troposféricas" (PDF) . Geophysical Research Letters . 33 (8): L08306. Bibcode :2006GeoRL..33.8306W. doi : 10.1029/2005GL025538 . hdl :1885/21511. Archivado (PDF) desde el original el 26 de noviembre de 2021 . Consultado el 18 de mayo de 2018 .
- ^ de Pater, Imke (2001). Ciencias Planetarias . Cambridge. pag. 34.ISBN 978-0521482196.
- ^ Ray, R. (15 de mayo de 2001). «Mareas oceánicas y rotación de la Tierra». Oficina especial de mareas del IERS. Archivado desde el original el 18 de agosto de 2000. Consultado el 17 de marzo de 2010 .
- ^ Murray, CD; Dermott, Stanley F. (1999). Dinámica del sistema solar . Cambridge University Press. pág. 184. ISBN 978-0-521-57295-8.
- ^ Dickinson, Terence (1993). Del Big Bang al Planeta X. Camden East, Ontario: Camden House . Págs. 79-81. ISBN. 978-0-921820-71-0.
- ^ ab Michaely, Erez; et al. (febrero de 2017), "Sobre la existencia de lunas exteriores regulares e irregulares que orbitan el sistema Plutón-Caronte", The Astrophysical Journal , 836 (1): 7, arXiv : 1506.08818 , Bibcode :2017ApJ...836...27M, doi : 10.3847/1538-4357/aa52b2 , S2CID 118068933, 27
- ^ Correia, Alexandre CM; Boué, Gwenaël; Laskar, Jacques (enero de 2012), "Aumento de la excentricidad de los exoplanetas por efecto de las mareas", The Astrophysical Journal Letters , 744 (2): 5, arXiv : 1111.5486 , Bibcode :2012ApJ...744L..23C, doi :10.1088/2041-8205/744/2/L23, S2CID 118695308, L23.
- ^ Colombo, G. (noviembre de 1965), "Período de rotación del planeta Mercurio", Nature , 208 (5010): 575, Bibcode :1965Natur.208..575C, doi : 10.1038/208575a0 , S2CID 4213296
- ^ Makarov, Valeri V. (junio de 2012), "Condiciones de paso y atrapamiento de planetas terrestres en resonancias de giro-órbita", The Astrophysical Journal , 752 (1): 8, arXiv : 1110.2658 , Bibcode :2012ApJ...752...73M, doi :10.1088/0004-637X/752/1/73, S2CID 119227632, 73
- ^ Schutz, Bernard (4 de diciembre de 2003). Gravedad desde el suelo. Cambridge University Press. pág. 43. ISBN 9780521455060Archivado desde el original el 6 de agosto de 2023. Consultado el 24 de abril de 2017 .
- ^ Showalter, MR; Hamilton, DP (junio de 2015). «Interacciones resonantes y rotación caótica de las pequeñas lunas de Plutón» (PDF) . Nature . 522 (7554): 45–49. Bibcode :2015Natur.522...45S. doi :10.1038/nature14469. PMID 26040889. S2CID 205243819. Archivado (PDF) desde el original el 2022-06-08 . Consultado el 2022-03-25 .
- ^ ab Szakáts, R.; Kiss, Cs.; Ortiz, JL; Morales, N.; Pál, A.; Müller, TG; et al. (2023). "Rotación bloqueada por mareas del planeta enano (136199) Eris descubierta a partir de fotometría terrestre y espacial a largo plazo". Astronomía y Astrofísica . L3 : 669. arXiv : 2211.07987 . Bibcode :2023A&A...669L...3S. doi :10.1051/0004-6361/202245234. S2CID 253522934.
- ^ Ortíz, JL; Cikota, A.; Cikota, S.; Hestroffer, D.; Thirouin, A.; Morales, N.; Duffard, R.; Gil-Hutton, R.; Santos-Sanz, P.; De La Cueva, I. (2010). "Un estudio astrométrico y fotométrico a mediano plazo del objeto transneptuniano (90482) Orcus". Astronomía y Astrofísica . 525 : A31. arXiv : 1010.6187 . Código Bib : 2011A&A...525A..31O. doi :10.1051/0004-6361/201015309. S2CID 56051949.
- ^ "7 de octubre de 1959: nuestra primera mirada al otro lado de la Luna". Universe Today . 2013-10-07. Archivado desde el original el 2022-08-12 . Consultado el 2015-02-15 .
- ^ Cain, Fraser (11 de abril de 2016). «¿Cuándo se acoplará la Tierra a la Luna?». Universe Today . Archivado desde el original el 28 de mayo de 2022. Consultado el 3 de agosto de 2020 .
- ^ Grego, Peter (2006). La Luna y cómo observarla. Springer Londres. pp. 47–50. ISBN 9781846282430Archivado desde el original el 21 de octubre de 2023. Consultado el 19 de marzo de 2023 .
- ^ ab Noyelles, Benoit; Frouard, Julien; Makarov, Valeri V. y Efroimsky, Michael (2014). "Revisión de la evolución de giro-órbita de Mercurio". Icarus . 241 : 26–44. arXiv : 1307.0136 . Código Bibliográfico :2014Icar..241...26N. doi :10.1016/j.icarus.2014.05.045. S2CID 53690707.
- ^ Gold, T.; Soter, S. (1969). "Mareas atmosféricas y la rotación resonante de Venus". Icarus . 11 (3): 356–366. Bibcode :1969Icar...11..356G. doi :10.1016/0019-1035(69)90068-2.
- ^ Barnes, Rory (2017). "Tidal blocking of habitable exoplanets". Mecánica celestial y astronomía dinámica . 129 (4). Springer: 509–536. arXiv : 1708.02981 . Código Bibliográfico : 2017CeMDA.129..509B. doi : 10.1007/s10569-017-9783-7. S2CID 119384474. Archivado desde el original el 26 de febrero de 2021. Consultado el 29 de marzo de 2021 .
- ^ Sean Raymond (20 de febrero de 2015). «Olvídense de los planetas parecidos a la Tierra: primero encontraremos extraterrestres en planetas similares a los que vemos en los ojos». Nautilus. Archivado desde el original el 23 de junio de 2017. Consultado el 5 de junio de 2017 .
- ^ Starr, Michelle (5 de enero de 2020). «Los planetas globo ocular podrían existir y son tan espeluznantes como parecen». ScienceAlert.com . Archivado desde el original el 6 de enero de 2020. Consultado el 6 de enero de 2020 .
- ^ ab Schirber, Michael (23 de mayo de 2005). "Role Reversal: Planet Controls a Star" (Inversión de roles: un planeta controla una estrella). space.com. Archivado desde el original el 4 de agosto de 2008. Consultado el 21 de abril de 2018 .
- ^ Singal, Ashok K. (mayo de 2014). "Vida en un planeta bloqueado por las mareas". Planex Newsletter . 4 (2): 8. arXiv : 1405.1025 . Código Bibliográfico :2014arXiv1405.1025S.
- ^ Walker, GAH; et al. (2008). "MOST detecta variabilidad en tau Bootis posiblemente inducida por su compañera planetaria". Astronomía y Astrofísica . 482 (2): 691–697. arXiv : 0802.2732 . Bibcode :2008A&A...482..691W. doi :10.1051/0004-6361:20078952. S2CID 56317105. Archivado desde el original el 25 de febrero de 2021 . Consultado el 16 de mayo de 2019 .
- ^ B. Gladman; et al. (1996). "Bloqueo sincrónico de satélites en evolución de marea". Icarus . 122 (1): 166–192. Bibcode :1996Icar..122..166G. doi : 10.1006/icar.1996.0117 .(Véase las páginas 169-170 de este artículo. Aquí se cita la fórmula (9), que proviene de S. J. Peale, Rotation histories of the natural satellites , en JA Burns, ed. (1977).Satélites planetarios. Tucson: University of Arizona Press. págs. 87–112.)
- ^ Hanslmeier, Arnold (2018). Habitabilidad planetaria y actividad estelar. World Scientific Publishing Company. pág. 99. ISBN 9789813237445Archivado desde el original el 4 de octubre de 2023. Consultado el 19 de marzo de 2023 .
- ^ Efroimsky, M. (2015). "Evolución de mareas de sistemas binarios asteroidales. Gobernada por la viscosidad. Ignorante de la rigidez". The Astronomical Journal . 150 (4): 12. arXiv : 1506.09157 . Bibcode :2015AJ....150...98E. doi :10.1088/0004-6256/150/4/98. S2CID 119283628. 98.
- ^ Nobili, AM (abril de 1978), "Efectos seculares de la fricción de las mareas en los sistemas planeta-satélite del sistema solar", La Luna y los Planetas , 18 (2): 203–216, Bibcode :1978M&P....18..203N, doi :10.1007/BF00896743, S2CID 121510792."Los siguientes satélites parecen corrotar: Fobos y Deimos, Amaltea, Ío, Europa, Ganimedes, Calisto, Jano, Mimas, Encélado, Tetis, Dione, Rea, Titán, Hiperión, Japeto, Miranda, Ariel, Umbriel, Titania y Oberón".
- ^ Peale, SJ (1988), "La dinámica rotacional de Mercurio y el estado de su núcleo", Mercury , University of Arizona Press: 461–493, Bibcode :1988merc.book..461P.
- ^ Rivoldini, A.; et al. (septiembre de 2010), "Disipación de mareas pasada y presente en Mercurio", Congreso Europeo de Ciencias Planetarias 2010 : 671, Bibcode :2010epsc.conf..671R.
- ^ "La órbita y la rotación de la Luna". Luna: NASA Science . Archivado desde el original el 2023-08-01 . Consultado el 2023-08-24 .
- ^ ab Correia, Alexandre CM (octubre de 2009), "Evolución secular de un satélite por efecto de marea: aplicación a Tritón", The Astrophysical Journal Letters , 704 (1): L1–L4, arXiv : 0909.4210 , Bibcode :2009ApJ...704L...1C, doi :10.1088/0004-637X/704/1/L1, S2CID 15378780.
- ^ Burns, JA (1978), "La evolución dinámica y el origen de las lunas marcianas", Vistas in Astronomy , 22 (2): 193–208, Bibcode :1978VA.....22..193B, doi :10.1016/0083-6656(78)90015-6.
- ^ abc Burns, Joseph A.; et al. (2004), Bagenal, Fran; Dowling, Timothy E.; McKinnon, William B. (eds.), "El sistema de anillos y lunas de Júpiter" (PDF) , Júpiter: el planeta, los satélites y la magnetosfera , Cambridge University Press, págs. 241–262, Bibcode :2004jpsm.book..241B, ISBN 978-0-521-81808-7, archivado (PDF) del original el 12 de mayo de 2006 , consultado el 7 de mayo de 2021
- ^ abcde Dougherty, Michele K.; Spilker, Linda J. (junio de 2018), "Revisión de las lunas heladas de Saturno tras la misión Cassini", Reports on Progress in Physics , 81 (6): 065901, Bibcode :2018RPPh...81f5901D, doi :10.1088/1361-6633/aabdfb, hdl : 10044/1/63567 , PMID 29651989, S2CID 4810803, 065901
- ^ Cartwright, Richard J.; et al. (noviembre de 2018), "Material rojo en las grandes lunas de Urano: ¿polvo de los satélites irregulares?", Icarus , 314 : 210–231, arXiv : 1806.01809 , Bibcode :2018Icar..314..210C, doi :10.1016/j.icarus.2018.06.004, S2CID 119243937
- ^ Stooke, Philip J. (enero de 1994), "Las superficies de Larisa y Proteo", Tierra, Luna y Planetas , 65 (1): 3–54, Bibcode :1994EM&P...65...31S, doi :10.1007/BF00572198
- ^ FJ Ballesteros; A. Fernández-Soto; VJ Martínez (2019). "Título: Buceando en exoplanetas: ¿Son los mares de agua los más comunes?". Astrobiología . 19 (5): 642–654. doi :10.1089/ast.2017.1720. hdl : 10261/213115 . PMID 30789285. S2CID 73498809.
- ^ Brown, Michael E.; Butler, Bryan (julio de 2023). "Masas y densidades de planetas enanos satélites medidas con ALMA". The Planetary Science Journal . 4 (10): 11. arXiv : 2307.04848 . Bibcode :2023PSJ.....4..193B. doi : 10.3847/PSJ/ace52a .
- ^ Vergano, Dan (25 de abril de 2007). "Fuera de nuestro mundo: un planeta parecido a la Tierra". USA Today . Archivado desde el original el 23 de mayo de 2011. Consultado el 25 de mayo de 2010 .
- ^ "Los astrónomos encuentran el planeta más parecido a la Tierra hasta la fecha". Science, EE. UU . 29 de septiembre de 2010. Archivado desde el original el 2 de octubre de 2010 . Consultado el 30 de septiembre de 2010 .
- ^ "Gliese 581g, el planeta más parecido a la Tierra descubierto hasta ahora". The Daily Telegraph , Reino Unido. 30 de septiembre de 2010. Archivado desde el original el 2 de octubre de 2010. Consultado el 30 de septiembre de 2010 .
- ^ "Gliese 581". Catálogo abierto de exoplanetas . Archivado desde el original el 7 de abril de 2022. Consultado el 16 de mayo de 2019 .
- ^ "Gliese 581". Enciclopedia Británica . Archivado desde el original el 6 de agosto de 2023. Consultado el 16 de mayo de 2019 .
- ^ Makarov, VV; Berghea, C. y Efroimsky, M. (2012). "Evolución dinámica y resonancias de giro-órbita de exoplanetas potencialmente habitables: el caso de GJ 581d". The Astrophysical Journal . 761 (2): 83. arXiv : 1208.0814 . Código Bibliográfico :2012ApJ...761...83M. doi :10.1088/0004-637X/761/2/83. S2CID 926755. 83.
- ^ "El telescopio de la NASA revela el mayor grupo de planetas del tamaño de la Tierra en la zona habitable alrededor de una estrella" (nota de prensa). NASA. 22 de febrero de 2017. Archivado desde el original el 5 de marzo de 2017 . Consultado el 23 de febrero de 2017 .
- ^ Gillon, Michaël; Triaud, Amaury HMJ; Demory, Brice-Olivier; Jehin, Emmanuël; Agol, Eric; Deck, Katherine M.; Lederer, Susan M.; de Wit, Julien; Burdanov, Artem (23 de febrero de 2017). "Siete planetas terrestres templados alrededor de la estrella enana ultrafría cercana TRAPPIST-1". Nature . 542 (7642): 456–460. arXiv : 1703.01424 . Código Bibliográfico :2017Natur.542..456G. doi :10.1038/nature21360. ISSN 0028-0836. PMC 5330437 . PMID 28230125.





























