Mecánica de suelos

La mecánica de suelos es una rama de la física de suelos y la mecánica aplicada que describe el comportamiento de los suelos . Se diferencia de la mecánica de fluidos y la mecánica de sólidos en el sentido de que los suelos consisten en una mezcla heterogénea de fluidos (generalmente aire y agua) y partículas (generalmente arcilla , limo , arena y grava ), pero el suelo también puede contener sólidos orgánicos y otras materias. ^{[1] [2] [3] [4]} Junto con la mecánica de rocas , la mecánica de suelos proporciona la base teórica para el análisis en ingeniería geotécnica , ^[5] una subdisciplina de la ingeniería civil , y geología de ingeniería , una subdisciplina de la geología . La mecánica de suelos se utiliza para analizar las deformaciones y el flujo de fluidos dentro de estructuras naturales y artificiales que se apoyan o están hechas de suelo, o estructuras que están enterradas en suelos. ^[6] Las aplicaciones de ejemplo son cimientos de edificios y puentes, muros de contención, presas y sistemas de tuberías enterradas. Los principios de la mecánica del suelo también se utilizan en disciplinas relacionadas, como la ingeniería geofísica , la ingeniería costera , la ingeniería agrícola y la hidrología .

Este artículo describe la génesis y composición del suelo, la distinción entre la presión del agua intersticial y el esfuerzo efectivo intergranular , la acción capilar de los fluidos en los espacios porosos del suelo , la clasificación del suelo , la filtración y la permeabilidad , el cambio de volumen dependiente del tiempo debido a la expulsión de agua de los pequeños espacios porosos, también conocido como consolidación , la resistencia al corte y la rigidez de los suelos. La resistencia al corte de los suelos se deriva principalmente de la fricción entre las partículas y el enclavamiento, que son muy sensibles al esfuerzo efectivo. ^{[7] [6]} El artículo concluye con algunos ejemplos de aplicaciones de los principios de la mecánica del suelo, como la estabilidad de taludes, la presión lateral de la tierra en los muros de contención y la capacidad portante de las cimentaciones.

El mecanismo principal de creación del suelo es la erosión de la roca. Todos los tipos de roca ( roca ígnea , roca metamórfica y roca sedimentaria ) pueden descomponerse en pequeñas partículas para crear suelo. Los mecanismos de erosión son la erosión física, la erosión química y la erosión biológica ^{[1] [2] [3]} Las actividades humanas, como la excavación, las voladuras y la eliminación de desechos, también pueden crear suelo. A lo largo del tiempo geológico, los suelos enterrados profundamente pueden alterarse por la presión y la temperatura para convertirse en roca metamórfica o sedimentaria, y si se funden y solidifican nuevamente, completarían el ciclo geológico convirtiéndose en roca ígnea. ^[3]

La meteorización física incluye los efectos de la temperatura, la congelación y descongelación del agua en las grietas, la lluvia, el viento, el impacto y otros mecanismos. La meteorización química incluye la disolución de la materia que compone una roca y la precipitación en forma de otro mineral. Los minerales arcillosos, por ejemplo, pueden formarse por la meteorización del feldespato , que es el mineral más común presente en las rocas ígneas.

El componente mineral más común del limo y la arena es el cuarzo , también llamado sílice , cuyo nombre químico es dióxido de silicio. La razón por la que el feldespato es más común en las rocas, pero la sílice es más frecuente en los suelos, es que el feldespato es mucho más soluble que la sílice.

El limo , la arena y la grava son básicamente pequeños trozos de rocas rotas .

Según el Sistema Unificado de Clasificación de Suelos , los tamaños de partículas de limo están en el rango de 0,002 mm a 0,075 mm y las partículas de arena tienen tamaños en el rango de 0,075 mm a 4,75 mm.

Las partículas de grava son fragmentos de roca fragmentados cuyo tamaño oscila entre 4,75 mm y 100 mm. Las partículas más grandes que la grava se denominan cantos rodados y rocas. ^{[1] [2]}

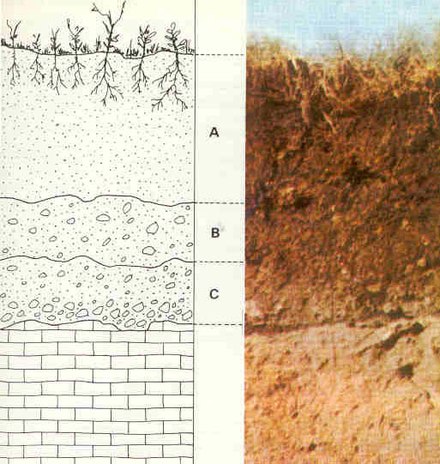
Los depósitos de suelo se ven afectados por el mecanismo de transporte y deposición hasta su ubicación. Los suelos que no son transportados se denominan suelos residuales: existen en el mismo lugar que la roca a partir de la cual se generaron. El granito descompuesto es un ejemplo común de suelo residual. Los mecanismos comunes de transporte son las acciones de la gravedad, el hielo, el agua y el viento. Los suelos arrastrados por el viento incluyen arenas de dunas y loess . El agua transporta partículas de diferentes tamaños según la velocidad del agua, por lo que los suelos transportados por el agua se clasifican según su tamaño. El limo y la arcilla pueden sedimentarse en un lago, y la grava y la arena se acumulan en el fondo del lecho de un río. Los depósitos de suelo arrastrados por el viento ( suelos eólicos ) también tienden a clasificarse según su tamaño de grano. La erosión en la base de los glaciares es lo suficientemente potente como para levantar rocas y cantos rodados grandes, así como suelo; los suelos que se desprenden al derretirse el hielo pueden ser una mezcla bien clasificada de tamaños de partículas muy variables. La gravedad por sí sola también puede transportar partículas desde la cima de una montaña para formar un montón de tierra y rocas en la base; los depósitos de suelo transportados por la gravedad se denominan coluvios . ^{[1] [2]}

El mecanismo de transporte también tiene un efecto importante en la forma de las partículas. Por ejemplo, la molienda a baja velocidad en el lecho de un río producirá partículas redondeadas. Las partículas de coluviales recién fracturadas suelen tener una forma muy angular.

Los limos, arenas y gravas se clasifican por su tamaño y, por lo tanto, pueden estar compuestos por una variedad de minerales. Debido a la estabilidad del cuarzo en comparación con otros minerales de roca, el cuarzo es el componente más común de la arena y el limo. La mica y el feldespato son otros minerales comunes presentes en las arenas y los limos. ^[1] Los componentes minerales de la grava pueden ser más similares a los de la roca madre.

Los minerales arcillosos más comunes son la montmorillonita o esmectita , la illita y la caolinita o caolín. Estos minerales tienden a formarse en estructuras similares a láminas o placas, con una longitud que varía típicamente entre 10 ⁻⁷  m y 4x10 ⁻⁶  m y un espesor que varía típicamente entre 10 ⁻⁹  m y 2x10 ⁻⁶  m, y tienen un área superficial específica relativamente grande. El área superficial específica (SSA) se define como la relación entre el área superficial de las partículas y la masa de las partículas. Los minerales arcillosos suelen tener áreas superficiales específicas en el rango de 10 a 1000 metros cuadrados por gramo de sólido. ^[3] Debido a la gran área superficial disponible para la interacción química, electrostática y de van der Waals , el comportamiento mecánico de los minerales arcillosos es muy sensible a la cantidad de fluido poroso disponible y al tipo y cantidad de iones disueltos en el fluido poroso. ^[1]

Los minerales de los suelos están formados predominantemente por átomos de oxígeno, silicio, hidrógeno y aluminio, organizados en diversas formas cristalinas. Estos elementos, junto con el calcio, el sodio, el potasio, el magnesio y el carbono, constituyen más del 99 por ciento de la masa sólida de los suelos. ^[1]

Los suelos consisten en una mezcla de partículas de diferentes tamaños, formas y mineralogías. Debido a que el tamaño de las partículas obviamente tiene un efecto significativo en el comportamiento del suelo, el tamaño de grano y la distribución del tamaño de grano se utilizan para clasificar los suelos. La distribución del tamaño de grano describe las proporciones relativas de partículas de varios tamaños. El tamaño de grano a menudo se visualiza en un gráfico de distribución acumulativa que, por ejemplo, traza el porcentaje de partículas más finas que un tamaño dado en función del tamaño. El tamaño de grano medio, , es el tamaño para el cual el 50% de la masa de partículas consiste en partículas más finas. El comportamiento del suelo, especialmente la conductividad hidráulica , tiende a estar dominado por las partículas más pequeñas, por lo tanto, el término "tamaño efectivo", denotado por , se define como el tamaño para el cual el 10% de la masa de partículas consiste en partículas más finas.$Estilo de visualización D_{50}$$Estilo de visualización D_{10}$

Las arenas y gravas que poseen una amplia gama de tamaños de partículas con una distribución uniforme de tamaños de partículas se denominan suelos bien calibrados . Si las partículas de suelo en una muestra se encuentran predominantemente en un rango relativamente estrecho de tamaños, la muestra está calibrada uniformemente . Si una muestra de suelo tiene huecos distintivos en la curva de gradación, por ejemplo, una mezcla de grava y arena fina, sin arena gruesa, la muestra puede estar calibrada por huecos . Tanto los suelos calibrados uniformemente como los calibrados por huecos se consideran mal calibrados . Existen muchos métodos para medir la distribución del tamaño de partículas . Los dos métodos tradicionales son el análisis por tamiz y el análisis por hidrómetro.

La distribución de tamaño de las partículas de grava y arena se mide típicamente usando análisis de tamiz. El procedimiento formal se describe en ASTM D6913-04 (2009). ^[8] Se utiliza una pila de tamices con orificios dimensionados con precisión entre una malla de alambres para separar las partículas en contenedores de tamaño. Un volumen conocido de tierra seca, con terrones descompuestos en partículas individuales, se coloca en la parte superior de una pila de tamices ordenados de grueso a fino. La pila de tamices se agita durante un período de tiempo estándar para que las partículas se clasifiquen en contenedores de tamaño. Este método funciona razonablemente bien para partículas en el rango de tamaño de arena y grava. Las partículas finas tienden a pegarse entre sí y, por lo tanto, el proceso de tamizado no es un método efectivo. Si hay una gran cantidad de finos (limo y arcilla) presentes en el suelo, puede ser necesario hacer pasar agua a través de los tamices para lavar las partículas gruesas y los terrones.

Hay una variedad de tamaños de tamices disponibles. El límite entre arena y limo es arbitrario. Según el Sistema Unificado de Clasificación de Suelos , un tamiz n.° 4 (4 aberturas por pulgada) con un tamaño de abertura de 4,75 mm separa la arena de la grava y un tamiz n.° 200 con una abertura de 0,075 mm separa la arena del limo y la arcilla. Según la norma británica, 0,063 mm es el límite entre arena y limo, y 2 mm es el límite entre arena y grava. ^[3]

La clasificación de los suelos de grano fino, es decir, los suelos que son más finos que la arena, se determina principalmente por sus límites de Atterberg , no por su tamaño de grano. Si es importante determinar la distribución del tamaño de grano de los suelos de grano fino, se puede realizar la prueba del hidrómetro. En las pruebas del hidrómetro, las partículas del suelo se mezclan con agua y se agitan para producir una suspensión diluida en un cilindro de vidrio, y luego el cilindro se deja reposar. Se utiliza un hidrómetro para medir la densidad de la suspensión en función del tiempo. Las partículas de arcilla pueden tardar varias horas en asentarse más allá de la profundidad de medición del hidrómetro. Las partículas de arena pueden tardar menos de un segundo. La ley de Stokes proporciona la base teórica para calcular la relación entre la velocidad de sedimentación y el tamaño de partícula. ASTM proporciona los procedimientos detallados para realizar la prueba del hidrómetro.

Las partículas de arcilla pueden ser lo suficientemente pequeñas como para no sedimentarse nunca porque se mantienen en suspensión mediante el movimiento browniano , en cuyo caso pueden clasificarse como coloides .

Existen diversos parámetros que se utilizan para describir las proporciones relativas de aire, agua y sólidos en un suelo. En esta sección se definen estos parámetros y algunas de sus interrelaciones. ^{[2] [6]} La notación básica es la siguiente:

$Estilo de visualización V_{a}}$, , y representan los volúmenes de aire, agua y sólidos en una mezcla de suelo;$Estilo de visualización V_ {w}$${\displaystyle V_{s}}$

$Estilo de visualización W_{a}}$, , y representan los pesos del aire, el agua y los sólidos en una mezcla de suelo;$Estilo de visualización W_ {w}}$${\displaystyle W_{s}}$

$Estilo de visualización M_{a}$, , y representan las masas de aire, agua y sólidos en una mezcla de suelo;$Estilo de visualización M_{w}}$${\displaystyle M_{s}}$

${\displaystyle \rho_{a}}$, , y representan las densidades de los componentes (aire, agua y sólidos) en una mezcla de suelo;${\displaystyle \rho_{w}}$${\displaystyle \rho _{s}}$

Nótese que los pesos, W, se pueden obtener multiplicando la masa, M, por la aceleración debida a la gravedad, g; por ejemplo,${\displaystyle W_{s}=M_{s}g}$

La gravedad específica es la relación entre la densidad de un material y la densidad del agua pura ( ).${\displaystyle \rho _{w}=1g/cm^{3}}$

Gravedad específica de los sólidos ,${\displaystyle G_{s}={\frac {\rho _{s}}{\rho _{w}}}}$

Téngase en cuenta que el peso específico , convencionalmente denotado por el símbolo, puede obtenerse multiplicando la densidad ( ) de un material por la aceleración debida a la gravedad, .${\displaystyle \gamma }$${\displaystyle \rho }$${\displaystyle g}$

Densidad ,densidad aparente o densidad húmeda son nombres diferentes para la densidad de la mezcla, es decir, la masa total de aire, agua y sólidos dividida por el volumen total de aire, agua y sólidos (se supone que la masa del aire es cero para fines prácticos):${\displaystyle \rho }$

${\displaystyle \rho ={\frac {M_{s}+M_{w}}{V_{s}+V_{w}+V_{a}}}={\frac {M_{t}}{V_{t}}}}$

Densidad seca , , es la masa de sólidos dividida por el volumen total de aire, agua y sólidos:${\displaystyle \rho _{d}}$

${\displaystyle \rho _{d}={\frac {M_{s}}{V_{s}+V_{w}+V_{a}}}={\frac {M_{s}}{V_{t}}}}$

Densidad de flotabilidad , definida como la densidad de la mezcla menos la densidad del agua, es útil si el suelo está sumergido bajo el agua:${\displaystyle \rho '}$

${\displaystyle \rho '=\rho \ -\rho _{w}}$

¿Dónde está la densidad del agua?${\displaystyle \rho _{w}}$

El contenido de agua es la relación entre la masa de agua y la masa de sólidos. Se mide fácilmente pesando una muestra de suelo, secándola en un horno y volviéndola a pesar. La ASTM describe los procedimientos estándar.${\displaystyle w}$

${\displaystyle w={\frac {M_{w}}{M_{s}}}={\frac {W_{w}}{W_{s}}}}$

La relación de huecos , , es la relación entre el volumen de huecos y el volumen de sólidos:${\displaystyle e}$

${\displaystyle e={\frac {V_{v}}{V_{s}}}={\frac {V_{v}}{V_{T}-V_{V}}}={\frac {n}{1-n}}}$

La porosidad ,es la relación entre el volumen de huecos y el volumen total, y está relacionada con la relación de huecos:${\displaystyle n}$

${\displaystyle n={\frac {V_{v}}{V_{t}}}={\frac {V_{v}}{V_{s}+V_{v}}}={\frac {e}{1+e}}}$

El grado de saturación , es la relación entre el volumen de agua y el volumen de huecos:${\displaystyle S}$

${\displaystyle S={\frac {V_{w}}{V_{v}}}}$

De las definiciones anteriores, se pueden derivar algunas relaciones útiles mediante el uso del álgebra básica.

${\displaystyle \rho ={\frac {(G_{s}+Se)\rho _{w}}{1+e}}}$

${\displaystyle \rho ={\frac {(1+w)G_{s}\rho _{w}}{1+e}}}$

${\displaystyle w={\frac {Se}{G_{s}}}}$

Los ingenieros geotécnicos clasifican los tipos de partículas del suelo realizando pruebas en muestras de suelo alteradas (secas, pasadas por tamices y remodeladas). Esto proporciona información sobre las características de los granos del suelo en sí. La clasificación de los tipos de granos presentes en un suelo no tiene en cuenta los efectos importantes de la estructura o la composición del suelo, términos que describen la compacidad de las partículas y los patrones en la disposición de las partículas en un marco de soporte de carga, así como el tamaño de los poros y las distribuciones de fluidos en los poros. Los geólogos ingenieros también clasifican los suelos en función de su génesis y su historia de sedimentación.

En los EE. UU. y otros países, se suele utilizar el Sistema Unificado de Clasificación de Suelos (USCS) para la clasificación de suelos. Otros sistemas de clasificación incluyen la Norma Británica BS 5930 y el sistema de clasificación de suelos AASHTO . ^[3]

En el USCS, las gravas (símbolo G ) y las arenas (símbolo S ) se clasifican según su distribución de tamaño de grano. Para el USCS, las gravas pueden recibir el símbolo de clasificación GW (grava bien clasificada), GP (grava mal clasificada), GM (grava con una gran cantidad de limo) o GC (grava con una gran cantidad de arcilla). Del mismo modo, las arenas pueden clasificarse como SW , SP , SM o SC . Las arenas y gravas con una cantidad pequeña pero no despreciable de finos (5-12%) pueden recibir una clasificación dual, como SW-SC .

Las arcillas y los limos, a menudo llamados "suelos de grano fino", se clasifican según sus límites de Atterberg ; los límites de Atterberg más comúnmente utilizados son el límite líquido (denotado por LL o ), el límite plástico (denotado por PL o ) y el límite de contracción (denotado por SL ).${\displaystyle w_{l}}$${\displaystyle w_{p}}$

El límite líquido es el contenido de agua en el que el comportamiento del suelo pasa de ser un sólido plástico a un líquido. El límite plástico es el contenido de agua en el que el comportamiento del suelo pasa de ser un sólido plástico a un sólido frágil. El límite de contracción corresponde a un contenido de agua por debajo del cual el suelo no se encogerá al secarse. La consistencia de un suelo de grano fino varía en proporción al contenido de agua del suelo.

Como las transiciones de un estado a otro son graduales, las pruebas han adoptado definiciones arbitrarias para determinar los límites de los estados. El límite líquido se determina midiendo el contenido de agua para el cual una ranura se cierra después de 25 golpes en una prueba estándar. ^[9] Alternativamente, se puede utilizar un aparato de prueba de cono de caída para medir el límite líquido. La resistencia al corte sin drenaje del suelo remodelado en el límite líquido es de aproximadamente 2 kPa. ^{[4] [10]} El límite plástico es el contenido de agua por debajo del cual no es posible apisonar el suelo a mano en cilindros de 3 mm de diámetro. El suelo se agrieta o se rompe a medida que se apisona hasta este diámetro. El suelo remodelado en el límite plástico es bastante rígido, con una resistencia al corte sin drenaje del orden de aproximadamente 200 kPa. ^{[4] [10]}

El índice de plasticidad de una muestra de suelo en particular se define como la diferencia entre el límite líquido y el límite plástico de la muestra; es un indicador de cuánta agua pueden absorber las partículas de suelo en la muestra y se correlaciona con muchas propiedades de ingeniería como la permeabilidad, la compresibilidad, la resistencia al corte y otras. En general, la arcilla que tiene una alta plasticidad tiene una permeabilidad menor y también es difícil de compactar.

Según el Sistema Unificado de Clasificación de Suelos (USCS), los limos y las arcillas se clasifican trazando los valores de su índice de plasticidad y límite líquido en un gráfico de plasticidad. La línea A del gráfico separa las arcillas (con el símbolo USCS C ) de los limos (con el símbolo M ). LL=50% separa los suelos de alta plasticidad (con el símbolo modificador H ) de los suelos de baja plasticidad (con el símbolo modificador L ). Un suelo que se grafica por encima de la línea A y tiene LL>50% se clasificaría, por ejemplo, como CH . Otras clasificaciones posibles de limos y arcillas son ML , CL y MH . Si los límites de Atterberg se grafican en la región "rayada" del gráfico cerca del origen, los suelos reciben la clasificación dual 'CL-ML'.

Los efectos del contenido de agua sobre la resistencia de los suelos remodelados saturados se pueden cuantificar mediante el uso del índice de liquidez , LI :

${\displaystyle LI={\frac {w-PL}{LL-PL}}}$

Cuando el LI es 1, el suelo remodelado se encuentra en el límite líquido y tiene una resistencia al corte no drenado de aproximadamente 2 kPa. Cuando el suelo se encuentra en el límite plástico , el LI es 0 y la resistencia al corte no drenado es de aproximadamente 200 kPa. ^{[4] [11]}

La densidad de las arenas (suelos sin cohesión) a menudo se caracteriza por la densidad relativa,${\displaystyle D_{r}}$

${\displaystyle D_{r}={\frac {e_{max}-e}{e_{max}-e_{min}}}100\%}$

donde: es la "relación de vacíos máxima" correspondiente a un estado muy suelto, es la "relación de vacíos mínima" correspondiente a un estado muy denso y es la relación de vacíos in situ . Los métodos utilizados para calcular la densidad relativa se definen en ASTM D4254-00(2006). ^[12]${\displaystyle e_{max}}$${\displaystyle e_{min}}$${\displaystyle e}$

Por lo tanto, si la arena o la grava son muy densas y el suelo es extremadamente suelto e inestable.${\displaystyle D_{r}=100\%}$${\displaystyle D_{r}=0\%}$

Si las presiones de los fluidos en un depósito de suelo aumentan de manera uniforme con la profundidad, entonces prevalecerán las condiciones hidrostáticas y los fluidos no fluirán a través del suelo. es la profundidad por debajo del nivel freático. Sin embargo, si el nivel freático está en pendiente o hay un nivel freático elevado como se indica en el esquema adjunto, entonces se producirán filtraciones . Para la filtración en estado estacionario, las velocidades de filtración no varían con el tiempo. Si los niveles freáticos cambian con el tiempo o si el suelo está en proceso de consolidación, entonces no se aplican las condiciones de estado estacionario.${\displaystyle u=\rho _{w}gz_{w}}$${\displaystyle z_{w}}$

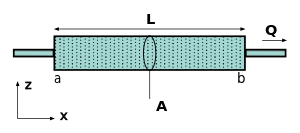
La ley de Darcy establece que el volumen de flujo del fluido intersticial a través de un medio poroso por unidad de tiempo es proporcional a la tasa de cambio de la presión excesiva del fluido con la distancia. La constante de proporcionalidad incluye la viscosidad del fluido y la permeabilidad intrínseca del suelo. Para el caso simple de un tubo horizontal lleno de tierra

${\displaystyle Q={\frac {-KA}{\mu }}{\frac {(u_{b}-u_{a})}{L}}}$

La descarga total (que tiene unidades de volumen por tiempo, p. ej., ft ³ /s o m ³ /s) es proporcional a la permeabilidad intrínseca , , el área de la sección transversal, , y la tasa de cambio de la presión de poro con la distancia, , e inversamente proporcional a la viscosidad dinámica del fluido, . El signo negativo es necesario porque los fluidos fluyen desde alta presión a baja presión. Por lo tanto, si el cambio de presión es negativo (en la dirección -), entonces el flujo será positivo (en la dirección -). La ecuación anterior funciona bien para un tubo horizontal, pero si el tubo estuviera inclinado de modo que el punto b estuviera a una elevación diferente que el punto a, la ecuación no funcionaría. El efecto de la elevación se explica reemplazando la presión de poro por el exceso de presión de poro , definida como:${\displaystyle Q}$${\displaystyle K}$${\displaystyle A}$${\displaystyle {\frac {u_{b}-u_{a}}{L}}}$${\displaystyle \mu }$${\displaystyle x}$${\displaystyle x}$${\displaystyle u_{e}}$

${\displaystyle u_{e}=u-\rho _{w}gz}$

donde es la profundidad medida a partir de una referencia de elevación arbitraria ( datum ). Reemplazando por obtenemos una ecuación más general para el flujo:${\displaystyle z}$${\displaystyle u}$${\displaystyle u_{e}}$

${\displaystyle Q={\frac {-KA}{\mu }}{\frac {(u_{e,b}-u_{e,a})}{L}}}$

Dividiendo ambos lados de la ecuación por , y expresando la tasa de cambio del exceso de presión de poro como una derivada , obtenemos una ecuación más general para la velocidad aparente en la dirección x:${\displaystyle A}$

${\displaystyle v_{x}={\frac {-K}{\mu }}{\frac {du_{e}}{dx}}}$

donde tiene unidades de velocidad y se denomina velocidad de Darcy (o velocidad específica de descarga , velocidad de filtración o velocidad superficial ). La velocidad intersticial o porosa es la velocidad media de las moléculas de fluido en los poros; está relacionada con la velocidad de Darcy y la porosidad a través de la relación de Dupuit-Forchheimer.${\displaystyle v_{x}=Q/A}$ ${\displaystyle v_{px}}$${\displaystyle n}$

${\displaystyle v_{px}={\frac {v_{x}}{n}}}$

(Algunos autores utilizan el término velocidad de filtración para referirse a la velocidad de Darcy, ^[13] mientras que otros lo utilizan para referirse a la velocidad de poro. ^[14] )

Los ingenieros civiles trabajan principalmente en problemas que involucran agua y en problemas relacionados con la Tierra (gravedad terrestre). Para esta clase de problemas, los ingenieros civiles suelen escribir la ley de Darcy de una forma mucho más simple: ^{[4] [6] [15]}

${\displaystyle v=ki}$

donde es la conductividad hidráulica , definida como , y es el gradiente hidráulico . El gradiente hidráulico es la tasa de cambio de la altura total con la distancia. La altura total, en un punto, se define como la altura (medida en relación con el punto de referencia) a la que subiría el agua en un piezómetro en ese punto. La altura total está relacionada con el exceso de presión del agua mediante:${\displaystyle k}$${\displaystyle k={\frac {K\rho _{w}g}{\mu _{w}}}}$${\displaystyle i}$${\displaystyle h}$

${\displaystyle u_{e}=\rho _{w}gh+Constant}$

y es cero si el dato para la medición de la altura se elige a la misma elevación que el origen para la profundidad, z se utiliza para calcular .${\displaystyle Constant}$${\displaystyle u_{e}}$

Los valores de conductividad hidráulica, , pueden variar en muchos órdenes de magnitud dependiendo del tipo de suelo. Las arcillas pueden tener una conductividad hidráulica tan pequeña como aproximadamente , las gravas pueden tener una conductividad hidráulica de hasta aproximadamente . La estratificación, la heterogeneidad y la perturbación durante el proceso de muestreo y prueba hacen que la medición precisa de la conductividad hidráulica del suelo sea un problema muy difícil. ^[4]${\displaystyle k}$${\displaystyle 10^{-12}{\frac {m}{s}}}$${\displaystyle 10^{-1}{\frac {m}{s}}}$

La Ley de Darcy se aplica en una, dos o tres dimensiones. ^[3] En dos o tres dimensiones, la filtración en estado estacionario se describe mediante la ecuación de Laplace . Hay programas informáticos disponibles para resolver esta ecuación. Pero tradicionalmente los problemas de filtración bidimensionales se resolvían utilizando un procedimiento gráfico conocido como red de flujo . ^{[3] [15] [16]} Un conjunto de líneas en la red de flujo está en la dirección del flujo de agua (líneas de flujo), y el otro conjunto de líneas está en la dirección de la carga total constante (líneas equipotenciales). Las redes de flujo se pueden utilizar para estimar la cantidad de filtración debajo de presas y tablestacas .

Cuando la velocidad de filtración es lo suficientemente grande, puede producirse erosión debido al arrastre por fricción ejercido sobre las partículas del suelo. La filtración vertical hacia arriba es una fuente de peligro en el lado de aguas abajo de las tablestacas y debajo de la base de una presa o dique. La erosión del suelo, conocida como "tubería de tierra", puede provocar la falla de la estructura y la formación de hundimientos . El agua que se filtra elimina la tierra, comenzando desde el punto de salida de la filtración, y la erosión avanza en sentido ascendente. ^[17] El término "ebullición de arena" se utiliza para describir la apariencia del extremo de descarga de una tubería de tierra activa. ^[18]

La filtración en dirección ascendente reduce la tensión efectiva dentro del suelo. Cuando la presión del agua en un punto del suelo es igual a la tensión vertical total en ese punto, la tensión efectiva es cero y el suelo no tiene resistencia por fricción a la deformación. Para una capa superficial, la tensión efectiva vertical se vuelve cero dentro de la capa cuando el gradiente hidráulico ascendente es igual al gradiente crítico. ^[15] Con una tensión efectiva cero, el suelo tiene muy poca resistencia y las capas de suelo relativamente impermeable pueden levantarse debido a las presiones del agua subyacente. La pérdida de resistencia debido a la filtración ascendente es un contribuyente común a las fallas de los diques. La condición de tensión efectiva cero asociada con la filtración ascendente también se llama licuefacción , arenas movedizas o condición de ebullición. Las arenas movedizas se denominaron así porque las partículas del suelo se mueven y parecen estar "vivas" (el significado bíblico de "rápido", en contraposición a "muerto"). (Tenga en cuenta que no es posible ser "succionado" hacia las arenas movedizas. Por el contrario, flotaría con aproximadamente la mitad de su cuerpo fuera del agua). ^[19]

Para entender la mecánica de los suelos es necesario entender cómo las tensiones normales y las tensiones de corte son compartidas por las diferentes fases. Ni el gas ni el líquido proporcionan una resistencia significativa a la tensión de corte . La resistencia de corte del suelo es proporcionada por la fricción y el entrelazamiento de las partículas. La fricción depende de las tensiones de contacto intergranular entre partículas sólidas. Las tensiones normales, por otro lado, son compartidas por el fluido y las partículas. ^[7] Aunque el aire de los poros es relativamente compresible y, por lo tanto, soporta poca tensión normal en la mayoría de los problemas geotécnicos, el agua líquida es relativamente incompresible y si los huecos están saturados de agua, el agua de los poros debe ser exprimida para empacar las partículas más juntas.

El principio de tensión efectiva, introducido por Karl Terzaghi , establece que la tensión efectiva σ' (es decir, la tensión intergranular promedio entre partículas sólidas) puede calcularse mediante una simple resta de la presión de poro de la tensión total:

${\displaystyle \sigma '=\sigma -u\,}$^[7]

donde σ es la tensión total y u es la presión de poro. No es práctico medir σ' directamente, por lo que en la práctica la tensión efectiva vertical se calcula a partir de la presión de poro y la tensión total vertical. La distinción entre los términos presión y tensión también es importante. Por definición, la presión en un punto es igual en todas las direcciones, pero las tensiones en un punto pueden ser diferentes en diferentes direcciones. En mecánica de suelos, las tensiones y presiones de compresión se consideran positivas y las tensiones de tracción se consideran negativas, lo que es diferente de la convención de signos de la mecánica de sólidos para la tensión.

En condiciones de terreno nivelado, la tensión vertical total en un punto, en promedio, es el peso de todo lo que se encuentra por encima de ese punto por unidad de área. La tensión vertical debajo de una capa superficial uniforme con densidad y espesor es, por ejemplo:${\displaystyle \sigma _{v}}$${\displaystyle \rho }$${\displaystyle H}$

${\displaystyle \sigma _{v}=\rho gH=\gamma H}$

donde es la aceleración debida a la gravedad y es el peso unitario de la capa suprayacente. Si hay varias capas de suelo o agua por encima del punto de interés, la tensión vertical se puede calcular sumando el producto del peso unitario y el espesor de todas las capas suprayacentes. La tensión total aumenta con la profundidad en proporción a la densidad del suelo suprayacente.${\displaystyle g}$${\displaystyle \gamma }$

No es posible calcular la tensión total horizontal de esta manera. Las presiones laterales de tierra se abordan en otra parte.

Si no hay flujo de agua intersticial en el suelo, las presiones de agua intersticial serán hidrostáticas . El nivel freático se encuentra a la profundidad donde la presión del agua es igual a la presión atmosférica. En condiciones hidrostáticas, la presión del agua aumenta linealmente con la profundidad por debajo del nivel freático:

${\displaystyle u=\rho _{w}gz_{w}}$

donde es la densidad del agua y es la profundidad debajo del nivel freático.${\displaystyle \rho _{w}}$${\displaystyle z_{w}}$

Debido a la tensión superficial, el agua se elevará en un pequeño tubo capilar por encima de una superficie libre de agua. Del mismo modo, el agua se elevará por encima del nivel freático hacia los pequeños espacios porosos alrededor de las partículas del suelo. De hecho, el suelo puede estar completamente saturado a cierta distancia por encima del nivel freático. Por encima de la altura de saturación capilar, el suelo puede estar húmedo, pero el contenido de agua disminuirá con la elevación. Si el agua en la zona capilar no se mueve, la presión del agua obedece a la ecuación de equilibrio hidrostático, , pero tenga en cuenta que , es negativo por encima del nivel freático. Por lo tanto, las presiones hidrostáticas del agua son negativas por encima del nivel freático. El espesor de la zona de saturación capilar depende del tamaño de los poros, pero normalmente, las alturas varían entre un centímetro o más para arena gruesa hasta decenas de metros para limo o arcilla. ^[3] De hecho, el espacio poroso del suelo es un fractal uniforme, por ejemplo, un conjunto de fractales D-dimensionales distribuidos uniformemente de tamaño lineal promedio L. Para el suelo arcilloso se ha encontrado que L = 0,15 mm y D = 2,7. ^[20]${\displaystyle u=\rho _{w}gz_{w}}$${\displaystyle z_{w}}$

La tensión superficial del agua explica por qué el agua no se escurre de un castillo de arena mojado o de una bola de arcilla húmeda. Las presiones negativas del agua hacen que el agua se adhiera a las partículas y las atraiga entre sí; la fricción en los contactos de las partículas hace que un castillo de arena sea estable. Pero tan pronto como un castillo de arena mojado se sumerge debajo de una superficie de agua libre, las presiones negativas se pierden y el castillo se derrumba. Teniendo en cuenta la ecuación de tensión efectiva, , si la presión del agua es negativa, la tensión efectiva puede ser positiva, incluso en una superficie libre (una superficie donde la tensión normal total es cero). La presión de poro negativa atrae las partículas entre sí y provoca fuerzas de contacto de compresión entre partículas. Las presiones de poro negativas en suelos arcillosos pueden ser mucho más potentes que las de la arena. Las presiones de poro negativas explican por qué los suelos arcillosos se encogen cuando se secan y se hinchan cuando se humedecen. La hinchazón y la contracción pueden causar grandes daños, especialmente a las estructuras ligeras y a las carreteras. ^[15]${\displaystyle \sigma '=\sigma -u,}$

En secciones posteriores de este artículo se abordan las presiones del agua intersticial en los problemas de filtración y consolidación.

• 
  Agua en contacto con partículas
• 
  Fuerza de contacto intergranular debida a la tensión superficial
• 
  Contracción causada por el secado

La consolidación es un proceso por el cual los suelos disminuyen de volumen. Ocurre cuando se aplica una tensión a un suelo que hace que las partículas del suelo se compacten más estrechamente, reduciendo así el volumen. Cuando esto ocurre en un suelo que está saturado de agua, el agua se expulsará del suelo. El tiempo necesario para exprimir el agua de un depósito grueso de capa de suelo arcilloso puede ser de años. Para una capa de arena, el agua puede expulsarse en cuestión de segundos. Los cimientos de un edificio o la construcción de un nuevo terraplén harán que el suelo de abajo se consolide y esto provocará un asentamiento que, a su vez, puede causar problemas en el edificio o terraplén. Karl Terzaghi desarrolló la teoría de la consolidación unidimensional que permite predecir la cantidad de asentamiento y el tiempo necesario para que se produzca el asentamiento. ^[21] Posteriormente, Maurice Biot desarrolló por completo la teoría de consolidación de suelos tridimensional, ampliando el modelo unidimensional desarrollado previamente por Terzaghi a hipótesis más generales e introduciendo el conjunto de ecuaciones básicas de Poroelasticidad . ^[7] Los suelos se prueban con un edómetro para determinar su índice de compresión y coeficiente de consolidación.

Cuando se elimina la tensión de un suelo consolidado, el suelo rebotará, atrayendo agua hacia los poros y recuperando parte del volumen que había perdido en el proceso de consolidación. Si se vuelve a aplicar la tensión, el suelo se volverá a consolidar a lo largo de una curva de recompresión, definida por el índice de recompresión. El suelo que se ha consolidado a una gran presión y se ha descargado posteriormente se considera sobreconsolidado . La tensión efectiva vertical pasada máxima se denomina tensión de preconsolidación . Un suelo que actualmente experimenta la tensión efectiva vertical pasada máxima se dice que está normalmente consolidado . La relación de sobreconsolidación (OCR) es la relación entre la tensión efectiva vertical pasada máxima y la tensión efectiva vertical actual. La OCR es significativa por dos razones: en primer lugar, porque la compresibilidad del suelo normalmente consolidado es significativamente mayor que la del suelo sobreconsolidado, y en segundo lugar, el comportamiento de corte y la dilatación del suelo arcilloso están relacionados con la OCR a través de la mecánica del suelo en estado crítico ; Los suelos arcillosos altamente sobreconsolidados son dilatantes, mientras que los suelos normalmente consolidados tienden a ser contractivos. ^{[2] [3] [4]}

La resistencia al corte y la rigidez del suelo determinan si el suelo será estable o no o cuánto se deformará. El conocimiento de la resistencia es necesario para determinar si una pendiente será estable, si un edificio o un puente pueden hundirse demasiado en el suelo y las presiones limitantes sobre un muro de contención. Es importante distinguir entre la falla de un elemento del suelo y la falla de una estructura geotécnica (por ejemplo, los cimientos de un edificio, una pendiente o un muro de contención); algunos elementos del suelo pueden alcanzar su resistencia máxima antes de la falla de la estructura. Se pueden utilizar diferentes criterios para definir la "resistencia al corte" y el " punto de fluencia " para un elemento del suelo a partir de una curva de tensión-deformación . Se puede definir la resistencia al corte máxima como el pico de una curva de tensión-deformación, o la resistencia al corte en el estado crítico como el valor después de grandes deformaciones cuando la resistencia al corte se estabiliza. Si la curva de tensión-deformación no se estabiliza antes del final de la prueba de resistencia al corte, a veces se considera que la "resistencia" es la resistencia al corte con una deformación del 15-20%. ^[15] La resistencia al corte del suelo depende de muchos factores, incluidos la tensión efectiva y la relación de huecos.

La rigidez de corte es importante, por ejemplo, para evaluar la magnitud de las deformaciones de las cimentaciones y de los taludes antes de que se produzca una falla y porque está relacionada con la velocidad de la onda de corte . La pendiente de la parte inicial, casi lineal, de un gráfico de la tensión de corte en función de la deformación de corte se denomina módulo de corte.

El suelo es un conjunto de partículas que tienen poca o ninguna cementación, mientras que la roca (como la arenisca) puede consistir en un conjunto de partículas que están fuertemente cementadas entre sí por enlaces químicos. La resistencia al corte del suelo se debe principalmente a la fricción entre partículas y, por lo tanto, la resistencia al corte en un plano es aproximadamente proporcional a la tensión normal efectiva en ese plano. ^[3] El ángulo de fricción interna está, por lo tanto, estrechamente relacionado con el ángulo de pendiente estable máximo, a menudo llamado ángulo de reposo .

Pero además de la fricción, el suelo obtiene una resistencia de corte significativa del entrelazado de los granos. Si los granos están densamente empaquetados, tienden a separarse unos de otros ya que están sujetos a una tensión de corte. La expansión de la matriz de partículas debido al corte fue llamada dilatación por Osborne Reynolds . ^[11] Si se considera la energía requerida para cortar un conjunto de partículas, hay una entrada de energía por la fuerza de corte, T, que se mueve una distancia, x, y también hay una entrada de energía por la fuerza normal, N, a medida que la muestra se expande una distancia, y. ^[11] Debido a la energía adicional requerida para que las partículas se dilaten contra las presiones de confinamiento, los suelos dilatantes tienen una mayor resistencia máxima que los suelos contractivos. Además, a medida que los granos del suelo dilatante se dilatan, se vuelven más sueltos (su relación de huecos aumenta) y su tasa de dilatación disminuye hasta que alcanzan una relación de huecos crítica. Los suelos contractivos se vuelven más densos a medida que se cortan, y su tasa de contracción disminuye hasta que alcanzan una relación de huecos crítica.

La tendencia de un suelo a dilatarse o contraerse depende principalmente de la presión de confinamiento y de la relación de huecos del suelo. La tasa de dilatación es alta si la presión de confinamiento es pequeña y la relación de huecos es pequeña. La tasa de contracción es alta si la presión de confinamiento es grande y la relación de huecos es grande. Como primera aproximación, las regiones de contracción y dilatación están separadas por la línea de estado crítico.

Una vez que un suelo alcanza el estado crítico, ya no se contrae ni se dilata y la tensión cortante en el plano de falla está determinada por la tensión normal efectiva en el plano de falla y el ángulo de fricción del estado crítico :${\displaystyle \tau _{crit}}$${\displaystyle \sigma _{n}'}$${\displaystyle \phi _{crit}'\ }$

${\displaystyle \tau _{crit}=\sigma _{n}'\tan \phi _{crit}'\ }$

Sin embargo, la resistencia máxima del suelo puede ser mayor debido a la contribución del entrelazamiento (dilatancia). Esto se puede afirmar:

${\displaystyle \tau _{peak}=\sigma _{n}'\tan \phi _{peak}'\ }$

Donde . Sin embargo, el uso de un ángulo de fricción mayor que el valor del estado crítico para el diseño requiere cuidado. La resistencia máxima no se movilizará en todas partes al mismo tiempo en un problema práctico como una base, una pendiente o un muro de contención. El ángulo de fricción del estado crítico no es tan variable como el ángulo de fricción máxima y, por lo tanto, se puede confiar en él con seguridad. ^{[3] [4] [11]}${\displaystyle \phi _{peak}'>\phi _{crit}'}$

Sin reconocer la importancia de la dilatación, Coulomb propuso que la resistencia al corte del suelo puede expresarse como una combinación de componentes de adhesión y fricción: ^[11]

${\displaystyle \tau _{f}=c'+\sigma _{f}'\tan \phi '\,}$

Ahora se sabe que los parámetros y en la última ecuación no son propiedades fundamentales del suelo. ^{[3] [6] [11] [22]} En particular, y son diferentes según la magnitud de la tensión efectiva. ^{[6] [22]} Según Schofield (2006), ^[11] el uso prolongado de en la práctica ha llevado a muchos ingenieros a creer erróneamente que es un parámetro fundamental. Esta suposición de que y son constantes puede llevar a una sobreestimación de las resistencias máximas. ^{[3] [22]}${\displaystyle c'}$${\displaystyle \phi '}$${\displaystyle c'}$${\displaystyle \phi '}$${\displaystyle c'}$${\displaystyle c'}$${\displaystyle c'}$${\displaystyle \phi '}$

Además de los componentes de fricción y enclavamiento (dilatancia) de la resistencia, la estructura y la estructura también desempeñan un papel importante en el comportamiento del suelo. La estructura y la estructura incluyen factores como el espaciamiento y la disposición de las partículas sólidas o la cantidad y distribución espacial del agua intersticial; en algunos casos, el material cementante se acumula en los contactos partícula-partícula. El comportamiento mecánico del suelo se ve afectado por la densidad de las partículas y su estructura o disposición de las partículas, así como por la cantidad y distribución espacial de los fluidos presentes (por ejemplo, agua y huecos de aire). Otros factores incluyen la carga eléctrica de las partículas, la química del agua intersticial, los enlaces químicos (es decir, la cementación: partículas conectadas a través de una sustancia sólida como el carbonato de calcio recristalizado) ^{[1] [22]}

La presencia de fluidos casi incompresibles , como el agua, en los espacios porosos, afecta la capacidad de los poros para dilatarse o contraerse.

Si los poros están saturados de agua, el agua debe ser succionada hacia los espacios de los poros que se dilatan para llenar los poros que se expanden (este fenómeno es visible en la playa cuando se forman manchas aparentemente secas alrededor de los pies que presionan la arena húmeda).

De manera similar, en el caso de un suelo contractivo, es necesario extraer el agua de los espacios porosos para permitir que se produzca la contracción.

La dilatación de los huecos provoca presiones negativas de agua que atraen el fluido hacia los poros, y la contracción de los huecos provoca presiones positivas de poro que empujan el agua fuera de los poros. Si la tasa de cizallamiento es muy grande en comparación con la tasa a la que el agua puede ser succionada o expulsada de los espacios de poros que se dilatan o contraen, entonces el cizallamiento se llama cizallamiento no drenado , si el cizallamiento es lo suficientemente lento como para que las presiones de agua sean insignificantes, el cizallamiento se llama cizallamiento drenado . Durante el cizallamiento no drenado, la presión de agua u cambia dependiendo de las tendencias de cambio de volumen. A partir de la ecuación de tensión efectiva, el cambio en u afecta directamente la tensión efectiva mediante la ecuación:

${\displaystyle \sigma '=\sigma -u\,}$

y la resistencia es muy sensible a la tensión efectiva. De ello se deduce que la resistencia al corte no drenado de un suelo puede ser menor o mayor que la resistencia al corte drenado dependiendo de si el suelo es contractivo o dilatativo.

Los parámetros de resistencia se pueden medir en el laboratorio mediante la prueba de corte directo , la prueba de corte triaxial , la prueba de corte simple, la prueba de cono de caída y la prueba de veleta de corte (manual) ; existen muchos otros dispositivos y variaciones de estos dispositivos que se utilizan en la práctica hoy en día. Las pruebas realizadas para caracterizar la resistencia y la rigidez de los suelos en el suelo incluyen la prueba de penetración de cono y la prueba de penetración estándar .

La relación tensión-deformación de los suelos, y por tanto la resistencia al corte, se ve afectada por: ^[23]

1. Composición del suelo (material básico del suelo): mineralogía, tamaño de grano y distribución del tamaño de grano, forma de las partículas, tipo y contenido de fluido poroso, iones en el grano y en el fluido poroso.
2. Estado (inicial): definido por la relación de vacíos inicial , la tensión normal efectiva y la tensión de corte (historial de tensión). El estado se puede describir con términos como: suelto, denso, sobreconsolidado, normalmente consolidado, rígido, blando, contractivo, dilatativo, etc.
3. Estructura : Se refiere a la disposición de las partículas dentro de la masa del suelo; la manera en que las partículas están compactadas o distribuidas. Las características tales como capas, juntas, fisuras, superficies resbaladizas, huecos, bolsas, cementación, etc., son parte de la estructura. La estructura de los suelos se describe mediante términos tales como: inalterado, perturbado, remodelado, compactado, cementado; floculento, en forma de panal, de grano único; floculado, desfloculado; estratificado, en capas, laminado; isotrópico y anisotrópico.
4. Condiciones de carga : trayectoria de tensión efectiva (drenada, no drenada) y tipo de carga (magnitud, velocidad [estática, dinámica]) e historial de tiempo (monótona, cíclica).

La teoría de la tensión lateral de la tierra se utiliza para estimar la cantidad de tensión que el suelo puede ejercer perpendicularmente a la gravedad. Esta es la tensión ejercida sobre los muros de contención . Un coeficiente de tensión lateral de la tierra, K, se define como la relación entre la tensión lateral (horizontal) efectiva y la tensión vertical efectiva para suelos sin cohesión (K = σ' _h / σ' _v ). Hay tres coeficientes: en reposo, activo y pasivo. La tensión en reposo es la tensión lateral en el suelo antes de que se produzca cualquier perturbación. El estado de tensión activa se alcanza cuando un muro se aleja del suelo bajo la influencia de la tensión lateral y resulta de una falla por corte debido a la reducción de la tensión lateral. El estado de tensión pasiva se alcanza cuando un muro se empuja dentro del suelo lo suficiente como para causar una falla por corte dentro de la masa debido al aumento de la tensión lateral. Hay muchas teorías para estimar la tensión lateral de la tierra; algunas tienen base empírica y otras se derivan analíticamente.

La capacidad de carga del suelo es la tensión de contacto promedio entre una base y el suelo que provocará una falla por corte en el suelo. La tensión de carga admisible es la capacidad de carga dividida por un factor de seguridad. A veces, en sitios con suelos blandos, pueden producirse grandes asentamientos bajo cimientos cargados sin que se produzca una falla por corte real; en tales casos, la tensión de carga admisible se determina con respecto al asentamiento máximo admisible. Es importante durante la etapa de construcción y diseño de un proyecto evaluar la resistencia de la subrasante. La prueba de relación de carga de California (CBR) se utiliza comúnmente para determinar la idoneidad de un suelo como subrasante para el diseño y la construcción. La prueba de carga de placa de campo se utiliza comúnmente para predecir las deformaciones y las características de falla del suelo/subrasante y el módulo de reacción de la subrasante (ks). El módulo de reacción de la subrasante (ks) se utiliza en el diseño de cimientos, estudios de interacción suelo-estructura y diseño de pavimentos de carreteras. ^{[ cita requerida ]}

El campo de la estabilidad de taludes abarca el análisis de la estabilidad estática y dinámica de taludes de presas de tierra y de roca, taludes de otros tipos de terraplenes, taludes excavados y taludes naturales en suelo y roca blanda. ^[24]

Como se ve a la derecha, las pendientes de tierra pueden desarrollar una zona de debilidad esférica cortada. La probabilidad de que esto ocurra se puede calcular de antemano utilizando un sencillo paquete de análisis circular en 2D. ^[25] Una de las principales dificultades del análisis es localizar el plano de deslizamiento más probable para una situación determinada. ^[26] Muchos deslizamientos de tierra se han analizado sólo después de que se han producido. Los deslizamientos de tierra frente a la resistencia de la roca son dos factores a tener en cuenta.

Un hallazgo reciente en mecánica de suelos es que la deformación del suelo puede describirse como el comportamiento de un sistema dinámico . Este enfoque de la mecánica de suelos se conoce como Mecánica de suelos basada en sistemas dinámicos (DSSM). La DSSM simplemente sostiene que la deformación del suelo es un proceso de Poisson en el que las partículas se mueven a su posición final con tensiones de corte aleatorias.

La base del DSSM es que los suelos (incluidas las arenas) pueden ser cizallados hasta que alcancen una condición de estado estable en la que, en condiciones de tasa de deformación constante, no hay cambios en la tensión de corte, la tensión de confinamiento efectiva y la relación de huecos. El estado estable fue definido formalmente ^[27] por Steve J. Poulos Archivado el 17 de octubre de 2020 en Wayback Machine, profesor asociado del Departamento de Mecánica de Suelos de la Universidad de Harvard, quien se basó en una hipótesis que Arthur Casagrande estaba formulando hacia el final de su carrera. La condición de estado estable no es la misma que la condición de "estado crítico". Se diferencia del estado crítico en que especifica una estructura estadísticamente constante en el estado estable. Los valores de estado estable también dependen muy ligeramente de la tasa de deformación.

Muchos sistemas en la naturaleza alcanzan estados estables, y la teoría de sistemas dinámicos describe tales sistemas. El esfuerzo cortante del suelo también puede describirse como un sistema dinámico. ^{[28] [29]} La base física del sistema dinámico de esfuerzo cortante del suelo es un proceso de Poisson en el que las partículas se mueven al estado estable con esfuerzos cortantes aleatorios. ^[30] Joseph ^[31] generalizó esto: las partículas se mueven a su posición final (no solo al estado estable) con esfuerzos cortantes aleatorios. Debido a sus orígenes en el concepto de estado estable, a la DSSM a veces se la llama informalmente "mecánica de suelos de Harvard".

El DSSM permite realizar ajustes muy precisos a las curvas de esfuerzo-deformación, incluso para las arenas. Debido a que sigue las condiciones en el plano de falla, también proporciona ajustes precisos para la región posterior a la falla de arcillas y limos sensibles, algo que otras teorías no pueden hacer. Además, el DSSM explica relaciones clave en la mecánica del suelo que hasta la fecha simplemente se han dado por sentado, por ejemplo, por qué las resistencias máximas al corte no drenadas normalizadas varían con el logaritmo de la relación de sobreconsolidación y por qué las curvas de esfuerzo-deformación se normalizan con el esfuerzo de confinamiento efectivo inicial; y por qué en la consolidación unidimensional la relación de vacíos debe variar con el logaritmo de la tensión vertical efectiva, por qué la curva de fin de primaria es única para los incrementos de carga estática y por qué la relación entre el valor de fluencia Cα y el índice de compresión Cc debe ser aproximadamente constante para una amplia gama de suelos. ^[32]

• Mecánica de suelos en estado crítico
• Ingeniería sísmica
• Ingeniería geológica
• Modelado geotécnico por centrifugación
• Ingeniería geotécnica
• Ingeniería geotécnica (Offshore)
• Geotecnia
• Hidrogeología , características del acuífero estrechamente relacionadas con las características del suelo.
• Sociedad Internacional de Mecánica de Suelos e Ingeniería Geotécnica
• Mecánica de rocas
• Análisis de estabilidad de taludes

• Medios relacionados con Mecánica de suelos en Wikimedia Commons