Espejo curvo

Un espejo curvo es un espejo con una superficie reflectante curva. La superficie puede ser convexa (que sobresale hacia afuera) o cóncava (que se hunde hacia adentro). La mayoría de los espejos curvos tienen superficies que tienen la forma de parte de una esfera , pero a veces se utilizan otras formas en dispositivos ópticos. El tipo no esférico más común son los reflectores parabólicos , que se encuentran en dispositivos ópticos como los telescopios reflectores que necesitan obtener imágenes de objetos distantes, ya que los sistemas de espejos esféricos, como las lentes esféricas , sufren aberración esférica . Los espejos distorsionadores se utilizan para el entretenimiento. Tienen regiones convexas y cóncavas que producen imágenes deliberadamente distorsionadas. También proporcionan imágenes muy aumentadas o muy disminuidas (más pequeñas) cuando el objeto se coloca a ciertas distancias.
Espejos convexos

Un espejo convexo o espejo divergente es un espejo curvo en el que la superficie reflectante se abulta hacia la fuente de luz. [1] Los espejos convexos reflejan la luz hacia el exterior, por lo que no se utilizan para enfocar la luz. Dichos espejos siempre forman una imagen virtual , ya que el punto focal ( F ) y el centro de curvatura ( 2F ) son puntos imaginarios "dentro" del espejo, a los que no se puede llegar. Como resultado, las imágenes formadas por estos espejos no se pueden proyectar en una pantalla, ya que la imagen está dentro del espejo. La imagen es más pequeña que el objeto, pero se hace más grande a medida que el objeto se acerca al espejo.
Un haz de luz colimado (paralelo) diverge (se dispersa) después de reflejarse en un espejo convexo, ya que la normal a la superficie difiere en cada punto del espejo.
Usos

.jpg/440px-The_Arnolfini_Portrait,_détail_(2).jpg)
El espejo retrovisor del lado del pasajero de un automóvil suele ser un espejo convexo. En algunos países, estos espejos llevan una advertencia de seguridad que dice " Los objetos en el espejo están más cerca de lo que parecen ", para advertir al conductor de los efectos distorsionadores del espejo convexo en la percepción de la distancia. Los espejos convexos son los preferidos en los vehículos porque dan una imagen vertical (no invertida), aunque disminuida (más pequeña), y porque proporcionan un campo de visión más amplio al estar curvados hacia afuera.
Estos espejos se encuentran a menudo en los pasillos de varios edificios (comúnmente conocidos como "espejos de seguridad de pasillo"), incluidos hospitales , hoteles , escuelas , tiendas y edificios de apartamentos . Por lo general, se montan en una pared o techo donde los pasillos se cruzan entre sí, o donde hacen curvas cerradas. Son útiles para que las personas observen cualquier obstrucción que enfrentarán en el próximo pasillo o después del siguiente giro. También se utilizan en carreteras , caminos de acceso y callejones para brindar seguridad a los usuarios de la carretera donde hay falta de visibilidad, especialmente en curvas y giros. [2]
Los espejos convexos se utilizan en algunos cajeros automáticos como una medida de seguridad sencilla y práctica que permite a los usuarios ver lo que sucede detrás de ellos. Se venden dispositivos similares para colocarlos en monitores de ordenadores comunes . Los espejos convexos hacen que todo parezca más pequeño, pero cubren un área de vigilancia mayor.
Los espejos redondos convexos llamados Oeil de Sorcière (del francés «ojo de brujo») fueron un artículo de lujo popular a partir del siglo XV, y se muestran en muchas representaciones de interiores de esa época. [3] Con la tecnología del siglo XV, era más fácil hacer un espejo curvo regular (de vidrio soplado) que uno perfectamente plano. También se los conocía como «ojos de banquero» debido a que su amplio campo de visión era útil para la seguridad. Entre los ejemplos famosos en el arte se incluyen el Retrato de Arnolfini de Jan van Eyck y el ala izquierda del Retablo de Werl de Robert Campin . [4]
Imagen

La imagen en un espejo convexo es siempre virtual ( los rayos no han pasado realmente a través de la imagen; sus extensiones sí, como en un espejo normal), disminuida (más pequeña) y derecha (no invertida). A medida que el objeto se acerca al espejo, la imagen se hace más grande, hasta aproximadamente el tamaño del objeto, cuando toca el espejo. A medida que el objeto se aleja, la imagen disminuye de tamaño y se acerca gradualmente al foco, hasta que se reduce a un punto en el foco cuando el objeto está a una distancia infinita. Estas características hacen que los espejos convexos sean muy útiles: dado que todo aparece más pequeño en el espejo, cubren un campo de visión más amplio que un espejo plano normal , por lo que son útiles para mirar los automóviles detrás del automóvil de un conductor en una carretera, observar un área más amplia para vigilancia, etc.
Espejos cóncavos

Un espejo cóncavo , o espejo convergente , tiene una superficie reflectante que está empotrada hacia adentro (lejos de la luz incidente). Los espejos cóncavos reflejan la luz hacia adentro, hacia un punto focal. Se utilizan para enfocar la luz. A diferencia de los espejos convexos, los espejos cóncavos muestran diferentes tipos de imágenes según la distancia entre el objeto y el espejo.
Los espejos se denominan "espejos convergentes" porque tienden a recoger la luz que cae sobre ellos, reorientando los rayos incidentes paralelos hacia un foco. Esto se debe a que la luz se refleja en diferentes ángulos en diferentes puntos del espejo, ya que la normal a la superficie del espejo difiere en cada punto.
Usos
Los espejos cóncavos se utilizan en telescopios reflectores . [5] También se utilizan para proporcionar una imagen ampliada de la cara para aplicar maquillaje o afeitarse. [6] En aplicaciones de iluminación , los espejos cóncavos se utilizan para recoger luz de una fuente pequeña y dirigirla hacia afuera en un haz como en linternas , faros y focos , o para recoger luz de un área grande y enfocarla en un punto pequeño, como en la energía solar concentrada . Los espejos cóncavos se utilizan para formar cavidades ópticas , que son importantes en la construcción de láseres . Algunos espejos dentales utilizan una superficie cóncava para proporcionar una imagen ampliada. El sistema de ayuda al aterrizaje por espejo de los portaaviones modernos también utiliza un espejo cóncavo.
Imagen
| Posición del objeto ( S ), punto focal ( F ) | Naturaleza de la imagen | Diagrama |
|---|---|---|
| (Objeto entre el punto focal y el espejo) |
|  |
| (Objeto en el punto focal) |
|  |
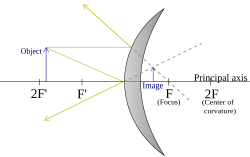
(Objeto entre el foco y el centro de curvatura) |
| 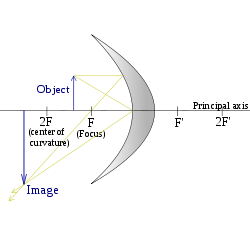 |
| (Objeto en el centro de curvatura) |
|  |
(Objeto más allá del centro de curvatura) |
| 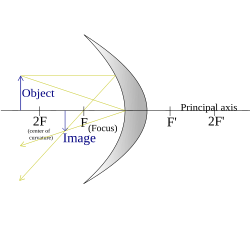 |
Forma de espejo
La mayoría de los espejos curvos tienen un perfil esférico. [7] Estos son los más simples de hacer y es la mejor forma para uso general. Sin embargo, los espejos esféricos sufren de aberración esférica : los rayos paralelos reflejados desde estos espejos no se enfocan en un solo punto. Para los rayos paralelos, como los que provienen de un objeto muy distante, un reflector parabólico puede hacer un mejor trabajo. Un espejo de este tipo puede enfocar los rayos paralelos entrantes en un punto mucho más pequeño que un espejo esférico. Un reflector toroidal es una forma de reflector parabólico que tiene una distancia focal diferente según el ángulo del espejo.
Análisis
Ecuación del espejo, aumento y distancia focal
La ecuación del espejo gaussiano , también conocida como ecuación del espejo y la lente, relaciona la distancia del objeto y la distancia de la imagen con la longitud focal : [2]
- .
La convención de signos que se utiliza aquí es que la distancia focal es positiva para espejos cóncavos y negativa para espejos convexos, y y son positivos cuando el objeto y la imagen están frente al espejo, respectivamente. (Son positivos cuando el objeto o la imagen son reales). [2]
En el caso de los espejos convexos, si se desplaza el término hacia el lado derecho de la ecuación para hallar , el resultado siempre es un número negativo, lo que significa que la distancia de la imagen es negativa (la imagen es virtual y se encuentra "detrás" del espejo). Esto es coherente con el comportamiento descrito anteriormente.
En el caso de los espejos cóncavos, el hecho de que la imagen sea virtual o real depende de la distancia entre el objeto y la distancia focal. Si el término es mayor que el término, entonces es positivo y la imagen es real. De lo contrario, el término es negativo y la imagen es virtual. Nuevamente, esto valida el comportamiento descrito anteriormente.
El aumento de un espejo se define como la altura de la imagen dividida por la altura del objeto:
- .
Por convención, si el aumento resultante es positivo, la imagen está en posición vertical. Si el aumento es negativo, la imagen está invertida (al revés).
Trazado de rayos
La ubicación y el tamaño de la imagen también se pueden determinar mediante el trazado gráfico de rayos, como se ilustra en las figuras anteriores. Un rayo dibujado desde la parte superior del objeto hasta el vértice de la superficie del espejo (donde el eje óptico se encuentra con el espejo) formará un ángulo con el eje óptico. El rayo reflejado tiene el mismo ángulo con el eje, pero en el lado opuesto (consulte Reflexión especular ).
Se puede trazar un segundo rayo desde la parte superior del objeto, paralelo al eje óptico. Este rayo se refleja en el espejo y pasa por su punto focal. El punto en el que se encuentran estos dos rayos es el punto de imagen correspondiente a la parte superior del objeto. Su distancia desde el eje óptico define la altura de la imagen, y su ubicación a lo largo del eje es la ubicación de la imagen. La ecuación del espejo y la ecuación de aumento se pueden derivar geométricamente considerando estos dos rayos. En su lugar, se puede considerar un rayo que va desde la parte superior del objeto a través del punto focal. Tal rayo se refleja paralelo al eje óptico y también pasa por el punto de imagen correspondiente a la parte superior del objeto.
Matriz de transferencia de rayos de espejos esféricos
El tratamiento matemático se realiza bajo la aproximación paraxial , es decir, bajo la primera aproximación un espejo esférico es un reflector parabólico . Aquí se muestra la matriz de rayos de un espejo esférico cóncavo. El elemento de la matriz es , donde es el punto focal del dispositivo óptico.
Los cuadros 1 y 3 muestran la suma de los ángulos de un triángulo y su comparación con π radianes (o 180°). El cuadro 2 muestra la serie de Maclaurin de hasta orden 1. Las derivaciones de las matrices de rayos de un espejo esférico convexo y una lente delgada son muy similares.
Véase también
- Problema de Alhazen (reflejo en un espejo esférico)
- Anamorfosis
- Energía solar concentrada : un método de generación de energía solar que utiliza espejos curvos o conjuntos de espejos.
- Lista de piezas y construcción del telescopio
Referencias
- ^ Nayak, Sanjay K.; Bhuvana, KP (2012). Ingeniería física. Nueva Delhi: Tata McGraw-Hill Education. pág. 6.4. ISBN 9781259006449.
- ^ abc Hecht, Eugene (1987). "5.4.3". Óptica (2.ª ed.). Addison Wesley. págs. 160-1. ISBN 0-201-11609-X.
- ^ Botteghe de Venecia: antigüedades, bisutería, café, pasteles, alfombras, cristal Archivado el 6 de marzo de 2017 en Wayback Machine.
- ^ Lorne Campbell, Catálogos de la Galería Nacional (nueva serie): Las pinturas neerlandesas del siglo XV , págs. 178-179, 188-189, 1998, ISBN 1-85709-171-X
- ^ Joshi, Dhiren M. Física de las ciencias vivas 10. Ratna Sagar. ISBN 9788183322904. Archivado desde el original el 18 de enero de 2018.
- ^ Anuario de Sura 2006 (inglés). Sura Books. ISBN 9788172541248. Archivado desde el original el 18 de enero de 2018.
- ^ Al-Azzawi, Abdul (26 de diciembre de 2006). Luz y óptica: principios y prácticas. CRC Press. ISBN 9780849383144. Archivado desde el original el 18 de enero de 2018.
Enlaces externos
- Aplicaciones Java para explorar el trazado de rayos para espejos curvos
- Espejos cóncavos: imágenes reales, Molecular Expressions Optical Microscopy Primer
- Espejos esféricos, laboratorio de física online
- "El pulido del espejo más grande del mundo" Popular Science , diciembre de 1935