Equilibrio dinámico
Equilibrio químico de una reacción reversible

En química , existe un equilibrio dinámico cuando se produce una reacción reversible . Las sustancias pasan de reactivos a productos a velocidades iguales , lo que significa que no hay cambio neto. Los reactivos y los productos se forman a una velocidad tal que la concentración de ninguno de ellos cambia. Es un ejemplo particular de un sistema en estado estacionario .

En física , en lo que respecta a la termodinámica , un sistema cerrado está en equilibrio termodinámico cuando las reacciones se producen a velocidades tales que la composición de la mezcla no cambia con el tiempo. De hecho, las reacciones se producen, a veces con mucha intensidad, pero en tal medida que no se pueden observar cambios en la composición. Las constantes de equilibrio se pueden expresar en términos de las constantes de velocidad para reacciones reversibles.

Ejemplos

En una botella nueva de refresco, la concentración de dióxido de carbono en la fase líquida tiene un valor particular. Si se vierte la mitad del líquido y se sella la botella, el dióxido de carbono abandonará la fase líquida a un ritmo cada vez menor, y la presión parcial del dióxido de carbono en la fase gaseosa aumentará hasta alcanzar el equilibrio. En ese punto, debido al movimiento térmico, una molécula de CO2 puede abandonar la fase líquida, pero en un tiempo muy breve otra molécula de CO2 pasará del gas al líquido, y viceversa. En el equilibrio, la velocidad de transferencia de CO2 de la fase gaseosa a la líquida es igual a la velocidad de líquido a gas. En este caso, la concentración de equilibrio de CO2 en el líquido viene dada por la ley de Henry , que establece que la solubilidad de un gas en un líquido es directamente proporcional a la presión parcial de ese gas sobre el líquido. [1] Esta relación se escribe como

do = K PAG {\displaystyle c=KP}

donde K es una constante dependiente de la temperatura, P es la presión parcial y c es la concentración del gas disuelto en el líquido. Por lo tanto, la presión parcial de CO2 en el gas ha aumentado hasta que se cumple la ley de Henry. La concentración de dióxido de carbono en el líquido ha disminuido y la bebida ha perdido parte de su efervescencia.

La ley de Henry se puede derivar al establecer que los potenciales químicos del dióxido de carbono en las dos fases sean iguales entre sí. La igualdad de potenciales químicos define el equilibrio químico . Otras constantes para el equilibrio dinámico que implican cambios de fase incluyen el coeficiente de partición y el producto de solubilidad . La ley de Raoult define la presión de vapor de equilibrio de una solución ideal.

El equilibrio dinámico también puede existir en un sistema monofásico. Un ejemplo sencillo es el del equilibrio ácido-base , como la disociación del ácido acético en una solución acuosa.

es 3 COOH ↽ − − ⇀ es 3 ARRULLO − + yo + {\displaystyle {\ce {CH3COOH <=> CH3COO- + H+}}}

En el equilibrio, el cociente de concentración , K , la constante de disociación ácida , es constante (sujeto a algunas condiciones).

K do = [ do yo 3 do Oh 2 − ] [ yo + ] [ do yo 3 do Oh 2 yo ] {\displaystyle K_{c}=\mathrm {\frac {[CH_{3}CO_{2}^{-}][H^{+}]}{[CH_{3}CO_{2}H]}} }

En este caso, la reacción directa implica la liberación de algunos protones de las moléculas de ácido acético y la reacción inversa implica la formación de moléculas de ácido acético cuando un ion acetato acepta un protón. El equilibrio se alcanza cuando la suma de los potenciales químicos de las especies del lado izquierdo de la expresión de equilibrio es igual a la suma de los potenciales químicos de las especies del lado derecho. Al mismo tiempo, las velocidades de las reacciones directa e inversa son iguales entre sí. Los equilibrios que implican la formación de complejos químicos también son equilibrios dinámicos y las concentraciones están gobernadas por las constantes de estabilidad de los complejos .

Los equilibrios dinámicos también pueden ocurrir en la fase gaseosa, como por ejemplo cuando se dimeriza el dióxido de nitrógeno .

2 NO 2 ↽ − − ⇀ norte 2 Oh 4 {\displaystyle {\ce {2NO2 <=> N2O4}}} ; K pag = [ norte 2 Oh 4 ] [ norte Oh 2 ] 2 {\displaystyle K_{p}=\mathrm {\frac {[N_{2}O_{4}]}{[NO_{2}]^{2}}} }

En la fase gaseosa, los corchetes indican la presión parcial. Alternativamente, la presión parcial de una sustancia puede escribirse como P(sustancia). [2]

Relación entre el equilibrio y las constantes de velocidad

En una reacción simple como la isomerización :

A ↽ − − ⇀ B {\displaystyle {\ce {A <=> B}}}

Hay dos reacciones a considerar, la reacción directa en la que la especie A se convierte en B y la reacción inversa en la que B se convierte en A. Si ambas reacciones son reacciones elementales , entonces la velocidad de reacción está dada por [3]

d [ A ] d a = − a F [ A ] a + a b [ B ] a {\displaystyle {\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}[{\ce {B}}]_{t}}

donde k f es la constante de velocidad para la reacción directa y k b es la constante de velocidad para la reacción inversa y los corchetes, […] , denotan la concentración . Si solo A está presente al comienzo, tiempo t = 0 , con una concentración [A] 0 , la suma de las dos concentraciones, [A] t y [B] t , en el tiempo t , será igual a [A] 0 .

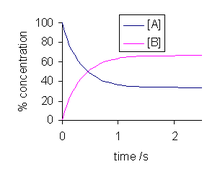
d [ A ] d a = − a F [ A ] a + a b ( [ A ] 0 − [ A ] a ) {\displaystyle {\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}([{\ce {A}}]_{0}-[{\ce {A}}]_{t}\right)}
% de concentraciones de especies en la reacción de isomerización. k f = 2 s −1 , k r = 1 s −1

La solución de esta ecuación diferencial es

[ A ] a = a b + a F mi − ( a F + a b ) a a F + a b [ A ] 0 {\displaystyle [{\ce {A}}]_{t}={\frac {k_{b}+k_{f}e^{-\left(k_{f}+k_{b}\right)t}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}

y se ilustra a la derecha. A medida que el tiempo tiende hacia el infinito, las concentraciones [A] t y [B] t tienden hacia valores constantes. Sea t la que se acerque al infinito, es decir, t → ∞ , en la expresión anterior:

[ A ] ∞ = a b a F + a b [ A ] 0 [ B ] ∞ = a F a F + a b [ A ] 0 {\displaystyle [{\ce {A}}]_{\infty }={\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{ 0}\qquad [{\ce {B}}]_{\infty }={\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_ {0}}

En la práctica, los cambios de concentración no serán medibles después de que las concentraciones no cambien después, por definición son concentraciones de equilibrio. Ahora, la constante de equilibrio para la reacción se define como a ⪆ 10 a F + a b . {\textstyle t\gtrapprox {\frac {10}{k_{f}+k_{b}}}.}

K = [ B ] ecualizador [ A ] ecualizador {\displaystyle K={\frac {[{\ce {B}}]_{\text{eq}}}{[{\ce {A}}]_{\text{eq}}}}}

De ello se deduce que la constante de equilibrio es numéricamente igual al cociente de las constantes de velocidad.

K = a F a F + a b [ A ] 0 a b a F + a b [ A ] 0 = a F a b {\displaystyle K={\frac {{\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}{{\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}}={\frac {k_{f}}{k_{b}}}}

En general, puede haber más de una reacción directa y más de una reacción inversa. Atkins afirma [3] que, para una reacción general, la constante de equilibrio global está relacionada con las constantes de velocidad de las reacciones elementales por

K = ( a F a b ) 1 × ( a F a b ) 2 × ⋯ {\displaystyle K=\left({\frac {k_{f}}{k_{b}}}\right)_{1}\times \left({\frac {k_{f}}{k_{b}}}\right)_{2}\times \cdots }

Véase también

Referencias

Atkins, PW; de Paula, J. (2006). Química física (8.ª ed.). Oxford University Press. ISBN 0-19-870072-5.

  1. ^ Atkins, Sección 5.3
  2. ^ Denbeigh, K (1981). Los principios del equilibrio químico (4.ª ed.). Cambridge, Reino Unido: Cambridge University Press. ISBN 0-521-28150-4.
  3. ^ ab Atkins, Sección 22.4
  • Ejemplo de equilibrio dinámico: Proyecto de demostraciones de Wolfram
Obtenido de "https://es.wikipedia.org/w/index.php?title=Equilibrio_dinámico&oldid=1249190709"