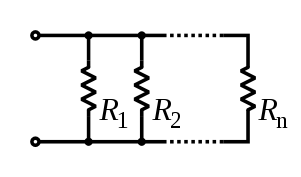
Circuitos en serie y en paralelo

Los componentes y redes eléctricas de dos terminales se pueden conectar en serie o en paralelo . La red eléctrica resultante tendrá dos terminales y puede participar en una topología en serie o en paralelo . El hecho de que un "objeto" de dos terminales sea un componente eléctrico (por ejemplo, un resistor ) o una red eléctrica (por ejemplo, resistores en serie) es una cuestión de perspectiva. En este artículo, se utilizará el término "componente" para referirse a un "objeto" de dos terminales que participa en las redes en serie/paralelo.
Los componentes conectados en serie están conectados a lo largo de un único "camino eléctrico", y cada componente tiene la misma corriente eléctrica a través de él, igual a la corriente a través de la red. El voltaje a través de la red es igual a la suma de los voltajes a través de cada componente. [1] [2]
Los componentes conectados en paralelo están conectados a lo largo de múltiples rutas y cada componente tiene el mismo voltaje , igual al voltaje a través de la red. La corriente a través de la red es igual a la suma de las corrientes a través de cada componente.
Las dos afirmaciones anteriores son equivalentes, excepto que intercambian el papel del voltaje y la corriente .
Un circuito compuesto únicamente por componentes conectados en serie se conoce como circuito en serie ; de igual modo, uno conectado completamente en paralelo se conoce como circuito en paralelo . Muchos circuitos pueden analizarse como una combinación de circuitos en serie y en paralelo, junto con otras configuraciones .
En un circuito en serie, la corriente que fluye a través de cada uno de los componentes es la misma, y el voltaje a través del circuito es la suma de las caídas de voltaje individuales a través de cada componente. [1] En un circuito en paralelo, el voltaje a través de cada uno de los componentes es el mismo, y la corriente total es la suma de las corrientes que fluyen a través de cada componente. [1]
Considere un circuito muy simple que consta de cuatro bombillas y una batería de automóvil de 12 voltios . Si un cable une la batería a una bombilla, a la siguiente, a la siguiente, a la siguiente y luego de nuevo a la batería en un bucle continuo, se dice que las bombillas están en serie. Si cada bombilla está conectada a la batería en un bucle separado, se dice que las bombillas están en paralelo. Si las cuatro bombillas están conectadas en serie, la misma corriente fluye a través de todas ellas y la caída de voltaje es de 3 voltios a través de cada bombilla, lo que puede no ser suficiente para hacerlas brillar. Si las bombillas están conectadas en paralelo, las corrientes a través de las bombillas se combinan para formar la corriente en la batería, mientras que la caída de voltaje es de 12 voltios a través de cada bombilla y todas brillan.
En un circuito en serie, todos los dispositivos deben funcionar para que el circuito esté completo. Si se funde una bombilla en un circuito en serie, se interrumpe todo el circuito. En los circuitos en paralelo, cada bombilla tiene su propio circuito, por lo que todas las bombillas, excepto una, podrían fundirse y la última seguiría funcionando.
Circuitos en serie
| Artículos sobre |
| Electromagnetismo |
|---|
 |
A los circuitos en serie a veces se los denomina circuitos acoplados por corriente. La corriente en un circuito en serie pasa por cada componente del circuito. Por lo tanto, todos los componentes en una conexión en serie transportan la misma corriente.
Un circuito en serie tiene un solo camino por el que puede circular la corriente. Abrir o interrumpir un circuito en serie en cualquier punto hace que todo el circuito se "abra" o deje de funcionar. Por ejemplo, si una sola de las bombillas de una cadena de luces navideñas antiguas se funde o se quita, toda la cadena deja de funcionar hasta que se reemplaza la bombilla defectuosa.
Actual
En un circuito en serie, la corriente es la misma para todos los elementos.
Voltaje
En un circuito en serie, el voltaje es la suma de las caídas de voltaje de los componentes individuales (unidades de resistencia).
Unidades de resistencia
La resistencia total de dos o más resistencias conectadas en serie es igual a la suma de sus resistencias individuales:
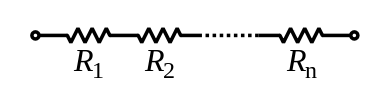 Aquí, el subíndice s en R s denota "serie", y R s denota resistencia en una serie.
Aquí, el subíndice s en R s denota "serie", y R s denota resistencia en una serie.
Conductancia
La conductancia eléctrica presenta una magnitud recíproca a la resistencia. Por lo tanto, la conductancia total de un circuito en serie de resistencias puras se puede calcular a partir de la siguiente expresión:
Para un caso especial de dos conductancias en serie, la conductancia total es igual a:
Inductores
Los inductores siguen la misma ley, en el sentido de que la inductancia total de los inductores no acoplados en serie es igual a la suma de sus inductancias individuales:
Sin embargo, en algunas situaciones, es difícil evitar que los inductores adyacentes se influyan entre sí, ya que el campo magnético de un dispositivo se acopla con los devanados de sus vecinos. Esta influencia se define por la inductancia mutua M. Por ejemplo, si dos inductores están en serie, hay dos inductancias equivalentes posibles según cómo se influyan entre sí los campos magnéticos de ambos inductores.
Cuando hay más de dos inductores, la inductancia mutua entre cada uno de ellos y la forma en que las bobinas se influyen entre sí complica el cálculo. Para un número mayor de bobinas, la inductancia combinada total viene dada por la suma de todas las inductancias mutuas entre las diversas bobinas, incluida la inductancia mutua de cada bobina dada consigo misma, lo que se denomina autoinductancia o simplemente inductancia. Para tres bobinas, hay seis inductancias mutuas , , y , y . También están las tres autoinductancias de las tres bobinas: , y .
Por lo tanto
Por reciprocidad, = de modo que los dos últimos grupos se pueden combinar. Los tres primeros términos representan la suma de las autoinductancias de las distintas bobinas. La fórmula se puede extender fácilmente a cualquier número de bobinas en serie con acoplamiento mutuo. El método se puede utilizar para encontrar la autoinductancia de bobinas grandes de alambre de cualquier forma de sección transversal calculando la suma de la inductancia mutua de cada vuelta de alambre en la bobina con cada una de las otras, ya que en una bobina de este tipo todas las vueltas están en serie.
Condensadores
Los capacitores siguen la misma ley utilizando los recíprocos. La capacidad total de los capacitores en serie es igual al recíproco de la suma de los recíprocos de sus capacidades individuales:
De manera equivalente, utilizando la elasticidad (el recíproco de la capacitancia), la elasticidad total en serie es igual a la suma de la elasticidad de cada capacitor.
Interruptores
Dos o más interruptores en serie forman una compuerta AND lógica ; el circuito solo transporta corriente si todos los interruptores están cerrados. Véase compuerta AND .
Pilas y baterías
Una batería es un conjunto de celdas electroquímicas . Si las celdas están conectadas en serie, el voltaje de la batería será la suma de los voltajes de las celdas. Por ejemplo, una batería de automóvil de 12 voltios contiene seis celdas de 2 voltios conectadas en serie. Algunos vehículos, como los camiones, tienen dos baterías de 12 voltios en serie para alimentar el sistema de 24 voltios.
Circuitos paralelos

Si dos o más componentes están conectados en paralelo, tienen la misma diferencia de potencial (voltaje) en sus extremos. Las diferencias de potencial entre los componentes son de la misma magnitud y también tienen polaridades idénticas. Se aplica el mismo voltaje a todos los componentes del circuito conectados en paralelo. La corriente total es la suma de las corrientes a través de los componentes individuales, de acuerdo con la ley de corriente de Kirchhoff .
Voltaje
En un circuito paralelo , el voltaje es el mismo para todos los elementos.
Actual
La corriente en cada resistencia individual se obtiene mediante la ley de Ohm . Al factorizar el voltaje se obtiene
Unidades de resistencia
Para hallar la resistencia total de todos los componentes, se suman los recíprocos de las resistencias de cada componente y se obtiene el recíproco de la suma. La resistencia total siempre será menor que el valor de la resistencia más pequeña:
Para sólo dos resistencias, la expresión no recíproca es razonablemente simple:
Esto a veces se conoce con el nombre mnemotécnico producto sobre suma .
Para N resistencias iguales en paralelo, la expresión de suma recíproca se simplifica a: y por lo tanto a:
Para encontrar la corriente en un componente con resistencia , utilice nuevamente la ley de Ohm:
Los componentes dividen la corriente según sus resistencias recíprocas, así, en el caso de dos resistencias,
Un término antiguo para los dispositivos conectados en paralelo es múltiple , como por ejemplo conexiones múltiples para lámparas de arco .
Conductancia
Dado que la conductancia eléctrica es recíproca a la resistencia, la expresión para la conductancia total de un circuito paralelo de resistencias es simplemente:
Las relaciones para la conductancia total y la resistencia se encuentran en una relación complementaria: la expresión para una conexión en serie de resistencias es la misma que para una conexión en paralelo de conductancias, y viceversa.
Inductores
Los inductores siguen la misma ley, en el sentido de que la inductancia total de los inductores no acoplados en paralelo es igual al recíproco de la suma de los recíprocos de sus inductancias individuales:
Si los inductores están situados en los campos magnéticos de cada uno, este enfoque no es válido debido a la inductancia mutua. Si la inductancia mutua entre dos bobinas en paralelo es M , el inductor equivalente es:
Si
El signo de depende de cómo se influyen entre sí los campos magnéticos. Para dos bobinas iguales acopladas estrechamente, la inductancia total es cercana a la de cada una de las bobinas. Si se invierte la polaridad de una bobina de modo que M sea negativa, entonces la inductancia paralela es casi cero o la combinación es casi no inductiva. Se supone que en el caso de "acoplamiento estrecho" M es casi igual a L . Sin embargo, si las inductancias no son iguales y las bobinas están acopladas estrechamente, pueden darse condiciones cercanas a un cortocircuito y corrientes circulantes altas para valores positivos y negativos de M , lo que puede causar problemas.
Más de tres inductores se vuelven más complejos y se debe considerar la inductancia mutua de cada inductor sobre cada uno de los otros inductores y su influencia mutua. Para tres bobinas, hay tres inductancias mutuas , y . Esto se maneja mejor con métodos matriciales y sumando los términos de la inversa de la matriz (3×3 en este caso).
Las ecuaciones pertinentes son de la forma:
Condensadores
La capacitancia total de los capacitores en paralelo es igual a la suma de sus capacitancias individuales:
El voltaje de trabajo de una combinación paralela de capacitores siempre está limitado por el voltaje de trabajo más pequeño de un capacitor individual.
Interruptores
Dos o más interruptores en paralelo forman una puerta lógica OR ; el circuito lleva corriente si al menos un interruptor está cerrado. Véase puerta OR .
Pilas y baterías
Si las celdas de una batería están conectadas en paralelo, el voltaje de la batería será el mismo que el voltaje de la celda, pero la corriente suministrada por cada celda será una fracción de la corriente total. Por ejemplo, si una batería consta de cuatro celdas idénticas conectadas en paralelo y suministra una corriente de 1 amperio , la corriente suministrada por cada celda será de 0,25 amperios. Si las celdas no son idénticas en voltaje, las celdas con voltajes más altos intentarán cargar las que tengan voltajes más bajos, lo que podría dañarlas.
Las baterías conectadas en paralelo se utilizaron ampliamente para alimentar los filamentos de las válvulas en las radios portátiles . Las baterías recargables de iones de litio (en particular, las baterías de las computadoras portátiles) a menudo se conectan en paralelo para aumentar la capacidad de amperios-hora. Algunos sistemas eléctricos solares tienen baterías en paralelo para aumentar la capacidad de almacenamiento; una aproximación cercana de los amperios-hora totales es la suma de todos los amperios-hora de las baterías en paralelo.
Combinando conductancias
De las leyes de circuitos de Kirchhoff se pueden deducir las reglas para combinar conductancias. Para dos conductancias y en paralelo , el voltaje a través de ellas es el mismo y de la ley de corriente de Kirchhoff (LKC) la corriente total es
Sustituyendo la ley de Ohm por conductancias se obtiene y la conductancia equivalente será,
Para dos conductancias y en serie la corriente a través de ellas será la misma y la Ley de Voltaje de Kirchhoff dice que el voltaje a través de ellas es la suma de los voltajes a través de cada conductancia, es decir,
Sustituyendo la ley de Ohm por la conductancia se obtiene, lo que a su vez da la fórmula para la conductancia equivalente,
Esta ecuación se puede reorganizar ligeramente, aunque este es un caso especial que solo se reorganizará de esta manera para dos componentes.
Para tres conductancias en serie,
Notación
El valor de dos componentes en paralelo a menudo se representa en ecuaciones mediante el operador paralelo , dos líneas verticales (∥), tomando prestada la notación de líneas paralelas de la geometría .
Esto simplifica expresiones que de otro modo se complicarían con la expansión de los términos. Por ejemplo:
Aplicaciones
Una aplicación común de los circuitos en serie en la electrónica de consumo es en las baterías, donde se utilizan varias celdas conectadas en serie para obtener un voltaje de funcionamiento conveniente. Dos celdas de zinc desechables en serie pueden alimentar una linterna o un control remoto a 3 voltios; el paquete de baterías de una herramienta eléctrica portátil puede contener una docena de celdas de iones de litio conectadas en serie para proporcionar 48 voltios.
Los circuitos en serie se utilizaban anteriormente para la iluminación de trenes eléctricos de varias unidades . Por ejemplo, si la tensión de alimentación era de 600 voltios, podía haber ocho bombillas de 70 voltios en serie (un total de 560 voltios) más una resistencia para reducir los 40 voltios restantes. Los circuitos en serie para la iluminación de trenes fueron reemplazados, primero por los motores-generadores y luego por los dispositivos de estado sólido .
La resistencia en serie también se puede aplicar a la disposición de los vasos sanguíneos dentro de un órgano determinado. Cada órgano está irrigado por una arteria grande, arterias más pequeñas, arteriolas, capilares y venas dispuestas en serie. La resistencia total es la suma de las resistencias individuales, como se expresa mediante la siguiente ecuación: R total = R arteria + R arteriolas + R capilares . La mayor proporción de resistencia en esta serie la aportan las arteriolas. [3]
La resistencia paralela se ilustra mediante el sistema circulatorio . Cada órgano está irrigado por una arteria que se ramifica desde la aorta . La resistencia total de esta disposición paralela se expresa mediante la siguiente ecuación: 1/ R total = 1/ R a + 1/ R b + ... + 1/ R n . R a , R b y R n son las resistencias de las arterias renal, hepática y otras respectivamente. La resistencia total es menor que la resistencia de cualquiera de las arterias individuales. [3]
Véase también
- Antiparalelo (electrónica)
- Combinando impedancias
- Divisor de corriente
- Transformadas de impedancia equivalente
- Analogía hidráulica
- Análisis de redes (circuitos eléctricos)
- Distancia de resistencia
- Dualidad serie-paralelo
- Orden parcial serie-paralelo
- Resortes en serie y en paralelo
- Topología (circuitos eléctricos)
- Divisor de voltaje
- Puente de Wheatstone
- Transformada Y-Δ
Referencias
- ^ abc Resnick, Robert; Halliday, David (1966). "Capítulo 32". Física . Vol. I y II (edición internacional combinada). Wiley . LCCN 66-11527. Ejemplo 1.
- ^ Smith, RJ (1966). Circuitos, dispositivos y sistemas (edición internacional). Nueva York: Wiley . pág. 21. LCCN 66-17612.
- ^ ab Costanzo, Linda S. Fisiología . Serie de revisiones de la junta. pág. 74.
Lectura adicional
- Williams, Tim (2005). El compañero del diseñador de circuitos . Butterworth-Heinemann . ISBN 0-7506-6370-7.
- "Combinaciones de resistencias: ¿Cuántos valores se pueden utilizar con resistencias de 1K ohm?". Revista EDN .
- Grotz, Bernhard (4 de enero de 2018). "Strömungswiderstand". Mechanik der Flüssigkeiten (en alemán).