Proyección ortográfica multivista

Parte de una serie sobre
Proyección gráfica
Planar Proyección paralela Proyección ortográfica Proyección isométrica Proyección oblicua Proyección en perspectiva Perspectiva curvilínea Reverse perspective
Views Bird's-eye view Cross section Cutaway drawing Exploded view drawing Fisheye lens Multiviews Panorama Worm's-eye view Zoom lens
Topics 3D projection Anamorphosis Axonometry Computer graphics Computer-aided design Descriptive geometry Engineering drawing Map projection Picture plane Plans (drawings) Projection (linear algebra) Projection plane Projective geometry Stereoscopy Technical drawing True length Vanishing point Video game graphics Viewing frustum
v t e

En dibujo técnico y gráficos por computadora , una proyección multivista es una técnica de ilustración mediante la cual se construye una serie estandarizada de imágenes ortográficas bidimensionales para representar la forma de un objeto tridimensional . Se producen hasta seis imágenes de un objeto (llamadas vistas primarias ), con cada plano de proyección paralelo a uno de los ejes de coordenadas del objeto. Las vistas se colocan unas respecto de otras de acuerdo con uno de dos esquemas: proyección de primer ángulo o proyección de tercer ángulo . En cada uno, las apariencias de las vistas pueden considerarse como proyectadas sobre planos que forman una caja de seis lados alrededor del objeto. Aunque se pueden dibujar seis lados diferentes, por lo general tres vistas de un dibujo brindan suficiente información para hacer un objeto tridimensional.

Estas tres vistas se conocen como vista frontal (también vista de elevación ), vista superior o vista en planta y vista final (también vista de perfil o vista en sección ).

Cuando el plano o eje del objeto representado no es paralelo al plano de proyección, y donde varios lados de un objeto son visibles en la misma imagen, se denomina vista auxiliar .

Para representar cada una de estas imágenes, se elige un rayo de visión (también llamado línea de proyección , rayo de proyección o línea de visión ) hacia el objeto, que determina en el objeto varios puntos de interés (por ejemplo, los puntos que son visibles cuando se mira el objeto a lo largo del rayo de visión); esos puntos de interés se asignan mediante una proyección ortográfica a puntos en algún plano geométrico (llamado plano de proyección o plano de imagen ) que es perpendicular al rayo de visión, creando así una representación 2D del objeto 3D.

Habitualmente, se eligen dos rayos de visión para cada uno de los tres ejes del sistema de coordenadas del objeto; es decir, paralelo a cada eje, el objeto puede verse en una de dos direcciones opuestas, lo que da un total de 6 proyecciones ortográficas (o "vistas") del objeto: ^[1]

• A lo largo de un eje vertical (a menudo el eje y ): las vistas superior e inferior , que se conocen como planos (porque muestran la disposición de las características en un plano horizontal, como un piso en un edificio).
• A lo largo de un eje horizontal (a menudo el eje z ): las vistas frontal y posterior , que se conocen como elevaciones (porque muestran las alturas de las características de un objeto como un edificio).
• A lo largo de un eje ortogonal (a menudo el eje x ): Las vistas izquierda y derecha , que también se conocen como elevaciones , siguen el mismo razonamiento.

Estos seis planos de proyección se entrecruzan entre sí, formando una caja alrededor del objeto, cuya construcción más uniforme es un cubo; tradicionalmente, estas seis vistas se presentan juntas proyectando primero el objeto 3D sobre las caras 2D de un cubo y luego "desplegando" las caras del cubo de manera que todas ellas estén contenidas dentro del mismo plano (es decir, el plano del medio en el que se presentarán todas las imágenes juntas, como una hoja de papel o un monitor de computadora, etc.). Sin embargo, incluso si las caras de la caja se despliegan de una manera estandarizada, existe una ambigüedad en cuanto a qué proyección se muestra en una cara en particular; el cubo tiene dos caras que son perpendiculares a un rayo de visión, y los puntos de interés pueden proyectarse sobre cualquiera de ellas, una elección que ha dado como resultado dos estándares predominantes de proyección:

1. Proyección de primer ángulo : en este tipo de proyección, se imagina que el objeto está en el primer cuadrante. Debido a que el observador normalmente mira desde el lado derecho del cuadrante para obtener la vista frontal, los objetos se interpondrán entre el observador y el plano de proyección. Por lo tanto, en este caso, se imagina que el objeto es transparente y se imagina que los proyectores se extienden desde varios puntos del objeto para encontrarse con el plano de proyección. Cuando estos puntos de encuentro se unen en orden en el plano, forman una imagen; por lo tanto, en la proyección de primer ángulo, cualquier vista se coloca de manera que represente el lado del objeto más alejado de él. La proyección de primer ángulo se utiliza a menudo en partes de Europa, por lo que a menudo se la llama proyección europea.
2. Proyección en tercer ángulo : en este tipo de proyección, se imagina que el objeto está en el tercer cuadrante. Nuevamente, como normalmente se supone que el observador mira desde el lado derecho del cuadrante para obtener la vista frontal, en este método, el plano de proyección se interpone entre el observador y el objeto. Por lo tanto, se supone que el plano de proyección es transparente. La intersección de este plano con los proyectores desde todos los puntos del objeto formaría una imagen en el plano transparente.

Las proyecciones multivista muestran las vistas principales de un objeto, cada una vista en una dirección paralela a uno de los ejes de coordenadas principales. Estas vistas principales se denominan planos y elevaciones . A veces se muestran como si el objeto hubiera sido cortado o seccionado para exponer el interior: estas vistas se denominan secciones .

Un plano es una vista de un objeto tridimensional visto verticalmente desde arriba (o, a veces, desde abajo ^{[ cita requerida ]} ). Puede dibujarse en la posición de un plano horizontal que pasa a través, por encima o por debajo del objeto. El contorno de una forma en esta vista a veces se denomina forma en planta , por ejemplo, en el caso de las alas de un avión .

La vista en planta desde arriba de un edificio se llama plano de tejado. Una sección vista en un plano horizontal a través de las paredes y que muestra el piso debajo se llama plano de planta .

La elevación es la vista de un objeto tridimensional desde la posición de un plano vertical junto a un objeto. En otras palabras, una elevación es una vista lateral, tal como se ve desde el frente, desde atrás, desde la izquierda o desde la derecha (y se denomina elevación frontal , elevación lateral [izquierda/derecha] y elevación trasera ).

Una elevación es un método común para representar la configuración externa y los detalles de un objeto tridimensional en dos dimensiones. Las fachadas de los edificios se muestran como elevaciones en los dibujos arquitectónicos y técnicos .

Las elevaciones son la proyección ortográfica más común para transmitir la apariencia de un edificio desde el exterior. Las perspectivas también se utilizan comúnmente para este propósito. La elevación de un edificio generalmente se etiqueta en relación con la dirección de la brújula hacia la que está orientada; la dirección desde la que una persona lo mira. Por ejemplo, la elevación norte de un edificio es el lado que está más cerca del norte verdadero en la brújula. ^[2]

Las elevaciones interiores se utilizan para mostrar detalles tales como carpintería y configuraciones de molduras.

En la industria de la construcción, las elevaciones son vistas de la estructura que no están en perspectiva. Se dibujan a escala para que se puedan tomar medidas de cualquier aspecto que sea necesario. Los conjuntos de dibujos incluyen elevaciones frontales, traseras y de ambos lados. Las elevaciones especifican la composición de las diferentes fachadas del edificio, incluidas las alturas de las cumbreras, la posición del desnivel final del terreno, los acabados exteriores, las pendientes del techo y otros detalles arquitectónicos.

Una elevación desarrollada es una variante de una vista de elevación regular en la que varios lados adyacentes no paralelos pueden mostrarse juntos como si se hubieran desplegado. Por ejemplo, las vistas norte y oeste pueden mostrarse una al lado de la otra, compartiendo un borde, aunque esto no represente una proyección ortográfica adecuada.

Una sección , o sección transversal , es una vista de un objeto tridimensional desde la posición de un plano a través del objeto.

Una sección es un método común para representar la disposición interna de un objeto tridimensional en dos dimensiones. Se utiliza a menudo en el dibujo técnico y tradicionalmente se raya con líneas cruzadas . El estilo de rayado con frecuencia indica el tipo de material por el que pasa la sección.

Con la tomografía axial computarizada , las computadoras construyen secciones transversales a partir de datos de rayos X.

• 
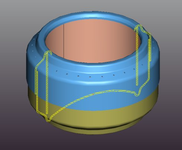
  Vista tridimensional de una estufa hecha con latas de bebidas, con una sección transversal en amarillo.
• 
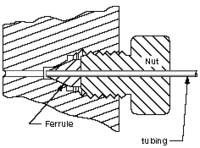
  Vista en sección transversal en 2D de un sello de compresión.
• 
  Corte transversal de un Porsche 996
• 
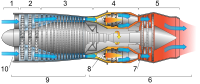
  Sección transversal de un motor a reacción
• 
  Vista en sección en diseño arquitectónico

Una vista auxiliar o pictórica es una vista ortográfica que se proyecta en cualquier plano que no sea una de las seis vistas principales . ^[3] Estas vistas se utilizan normalmente cuando un objeto tiene una superficie en un plano oblicuo. Al proyectar en un plano paralelo a la superficie oblicua, se muestra el tamaño y la forma reales de la superficie. Las vistas auxiliares se dibujan a menudo utilizando proyección isométrica .

This article needs editing to comply with Wikipedia's Manual of Style. Please help improve the content. (April 2014) (Learn how and when to remove this message)

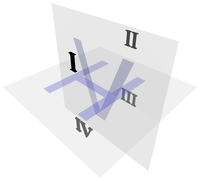
La proyección ortográfica moderna se deriva de la geometría descriptiva de Gaspard Monge . ^[4] Monge definió un sistema de referencia de dos planos de visión, el horizontal H ("suelo") y el vertical V ("telón de fondo"). Estos dos planos se intersecan para dividir el espacio 3D en 4 cuadrantes, que denominó:

• I : encima de H , delante de V
• II : encima de H , detrás de V
• III : debajo de H , detrás de V
• IV : debajo de H , delante de V

Estas etiquetas de cuadrante son las mismas que se utilizan en la geometría plana 2D, vistas desde una distancia infinita hacia la "izquierda", tomando H y V como el eje X y el eje Y , respectivamente.

El objeto 3D de interés se coloca entonces en el cuadrante I o III (equivalentemente, se desplaza la posición de la línea de intersección entre los dos planos), obteniendo proyecciones de primer y tercer ángulo , respectivamente. Los cuadrantes II y IV también son matemáticamente válidos, pero su uso daría como resultado una vista "verdadera" y la otra vista "invertida" 180° a través de su línea central vertical, lo que resulta demasiado confuso para los dibujos técnicos. (En los casos en que dicha vista es útil, por ejemplo, un techo visto desde arriba, se utiliza una vista reflejada, que es una imagen especular de la vista ortográfica verdadera).

La formulación original de Monge utiliza sólo dos planos y obtiene sólo las vistas superior y frontal. La adición de un tercer plano para mostrar una vista lateral (ya sea izquierda o derecha) es una extensión moderna. La terminología de cuadrante es un anacronismo leve, ya que una proyección ortográfica moderna con tres vistas corresponde con mayor precisión a un octante del espacio 3D.

En la proyección de primer ángulo , el objeto se ubica conceptualmente en el cuadrante I , es decir, flota por encima y delante de los planos de visión, los planos son opacos y cada vista se empuja a través del objeto hacia el plano más alejado de él. (Mnemotecnia: un "actor en un escenario"). Extendiéndose a la caja de 6 lados, cada vista del objeto se proyecta en la dirección (sentido) de la vista del objeto, sobre las paredes interiores (opacas) de la caja; es decir, cada vista del objeto se dibuja en el lado opuesto de la caja. Luego se crea una representación bidimensional del objeto "desplegando" la caja, para ver todas las paredes interiores . Esto produce dos plantas y cuatro elevaciones . Una forma más sencilla de visualizar esto es colocar el objeto sobre la parte superior de un recipiente al revés. Deslizar el objeto por el borde derecho del recipiente revela la vista lateral derecha.

• 
  Una imagen de un objeto en una caja.
• 
  La misma imagen, con vistas del objeto proyectadas en la dirección de la vista sobre las paredes utilizando la proyección del primer ángulo.
• 
  Imagen similar que muestra la caja desplegándose alrededor del objeto.
• 
  Imagen que muestra vistas ortográficas ubicadas entre sí de acuerdo con la proyección del primer ángulo.

En la proyección de tercer ángulo , el objeto se ubica conceptualmente en el cuadrante III, es decir, se coloca debajo y detrás de los planos de visualización, los planos son transparentes y cada vista se dibuja en el plano más cercano a él. (Mnemotecnia: un "tiburón en un tanque", esp. que está hundido en el piso). Usando la caja de visualización de 6 lados, cada vista del objeto se proyecta opuesta a la dirección (sentido) de la vista, sobre las paredes exteriores (transparentes) de la caja; es decir, cada vista del objeto se dibuja en el mismo lado de la caja. Luego, la caja se desdobla para ver todas sus paredes exteriores . Una forma más sencilla de visualizar esto es colocar el objeto en el fondo de un recipiente. Deslizar el objeto hacia arriba por el borde derecho del recipiente revela la vista del lado derecho.

Aquí se muestra la construcción de proyecciones en tercer ángulo del mismo objeto que el anterior. Observe que las vistas individuales son las mismas, solo que están dispuestas de manera diferente.

La proyección de primer ángulo es como si el objeto estuviera sobre el papel y, desde la vista de "cara" (frontal), se enrolla hacia la derecha para mostrar el lado izquierdo o se enrolla para mostrar su parte inferior. Es estándar en toda Europa y Asia (excepto Japón). La proyección de primer ángulo se usó ampliamente en el Reino Unido, pero durante la Segunda Guerra Mundial, los dibujos británicos enviados para ser fabricados en los EE. UU., como el Rolls-Royce Merlin , tuvieron que dibujarse en proyección de tercer ángulo antes de que pudieran producirse, por ejemplo, como el Packard V-1650 Merlin . Esto significó que algunas empresas británicas adoptaron por completo la proyección de tercer ángulo. BS 308 (Parte 1) Práctica de dibujo de ingeniería, dio la opción de usar ambas proyecciones, pero en general, cada ilustración (excepto las que explicaban la diferencia entre primer y tercer ángulo) se hizo en primer ángulo. Después de la retirada de la norma BS 308 en 1999, la norma BS 8888 ofreció la misma opción ya que hacía referencia directa a la norma ISO 5456-2, Dibujos técnicos – Métodos de proyección – Parte 2: Representaciones ortográficas.

El tercer ángulo es como si el objeto fuera una caja que se va a desplegar. Si desplegamos la caja de modo que la vista frontal esté en el centro de los dos brazos, entonces la vista superior está encima de ella, la vista inferior está debajo de ella, la vista izquierda está a la izquierda y la vista derecha está a la derecha. Es estándar en los EE. UU. ( ASME Y14.3-2003 lo especifica como el sistema de proyección predeterminado), Japón ( JIS B 0001:2010 lo especifica como el sistema de proyección predeterminado), Canadá y Australia ( AS1100.101 lo especifica como el sistema de proyección preferido).

Tanto la proyección del primer ángulo como la del tercer ángulo dan como resultado las mismas 6 vistas; la diferencia entre ellas es la disposición de estas vistas alrededor de la caja.

Se ha generado una gran confusión en las salas de dibujo y los departamentos de ingeniería cuando se transfieren los dibujos de una convención a otra. En los dibujos de ingeniería , la proyección se indica mediante un símbolo internacional que representa un cono truncado en la proyección del primer o tercer ángulo, como se muestra en el diagrama de la derecha.

La interpretación en 3D es un cono truncado sólido, con el extremo pequeño apuntando hacia el observador. La vista frontal es, por lo tanto, dos círculos concéntricos. El hecho de que el círculo interior esté dibujado con una línea continua en lugar de discontinua identifica esta vista como la vista frontal, no la vista posterior. La vista lateral es un trapezoide isósceles .

• En la proyección del primer ángulo , la vista frontal se empuja hacia la pared trasera y la vista lateral derecha se empuja hacia la pared izquierda, por lo que el símbolo del primer ángulo muestra el trapezoide con su lado más corto alejado de los círculos.
• En la proyección del tercer ángulo , la vista frontal se acerca a la pared frontal y la vista lateral derecha se acerca a la pared derecha, por lo que el símbolo del tercer ángulo muestra el trapezoide con su lado más corto hacia los círculos.

La proyección multivista ortográfica se deriva de los principios de la geometría descriptiva y puede producir una imagen de un objeto imaginario específico visto desde cualquier dirección del espacio. La proyección ortográfica se distingue por proyectores paralelos que emanan de todos los puntos del objeto representado y que se intersecan en ángulos rectos. Más arriba se describe una técnica que permite obtener distintas vistas proyectando imágenes después de que el objeto se gira a la posición deseada.

La geometría descriptiva tradicionalmente se basa en la obtención de varias vistas imaginando un objeto estacionario y cambiando la dirección de proyección (visión) para obtener la vista deseada.

Consulte la Figura 1. Si utiliza la técnica de rotación anterior, observe que no hay ninguna vista ortográfica disponible que mire perpendicularmente a ninguna de las superficies inclinadas. Supongamos que un técnico desea una vista de este tipo para, por ejemplo, mirar a través de un orificio que se perforará perpendicularmente a la superficie. Tal vista podría ser necesaria para calcular espacios libres o para fines de dimensionamiento. Para obtener esta vista sin múltiples rotaciones se requieren los principios de la geometría descriptiva. Los pasos a continuación describen el uso de estos principios en la proyección del tercer ángulo.

• Fig.1 : Representación gráfica del objeto imaginario que el técnico desea imaginar.
• Fig. 2 : El objeto se imagina detrás de un plano de proyección vertical. La esquina en ángulo del plano de proyección se aborda más adelante.
• Fig.3 : Los proyectores emanan paralelamente desde todos los puntos del objeto, perpendiculares al plano de proyección.
• Fig.4 : De este modo se crea una imagen.
• Fig.5 : Se añade un segundo plano de proyección horizontal, perpendicular al primero.
• Fig.6 : Los proyectores emanan paralelamente desde todos los puntos del objeto perpendiculares al segundo plano de proyección.
• Fig.7 : De este modo se crea una imagen.
• Fig.8 : Se añade el tercer plano de proyección, perpendicular a los dos anteriores.
• Fig.9 : Los proyectores emanan paralelamente desde todos los puntos del objeto perpendiculares al tercer plano de proyección.

• Fig.10 : De este modo se crea una imagen.
• Fig.11 : El cuarto plano de proyección se agrega paralelo a la superficie inclinada elegida y, forzosamente, perpendicular al primer plano de proyección (frontal).
• Fig.12 : Los proyectores emanan paralelos desde todos los puntos del objeto perpendicularmente a la superficie inclinada y, forzosamente, perpendiculares al cuarto plano (auxiliar) de proyección.
• Fig.13 : De este modo se crea una imagen.
• Fig.14-16 : Los distintos planos de proyección se despliegan para ser planares con el plano frontal de proyección.
• Fig.17 : Aspecto final de una proyección multivista ortográfica que incluye una "Vista auxiliar" que muestra la forma real de una superficie inclinada.

El primer ángulo se utiliza en la mayor parte del mundo. ^[5]

La proyección de tercer ángulo se utiliza con mayor frecuencia en Estados Unidos, ^[6] Japón (en JIS B 0001：2010); ^[7] y se prefiere en Australia, como se establece en AS 1100.101—1992 6.3.3. ^[8]

En el Reino Unido, BS8888 9.7.2.1 permite tres convenciones diferentes para organizar las vistas: vistas etiquetadas, proyección del tercer ángulo y proyección del primer ángulo.

• Dibujo arquitectónico
• Sección transversal (geometría)
• Dibujo de ingeniería
• Proyección gráfica
• Planos (dibujos)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Multiview orthographic projection" – news · newspapers · books · scholar · JSTOR (November 2009) (Learn how and when to remove this message)

BS 308 (Parte 1) Práctica de dibujo de ingeniería BS 8888 Documentación y especificación técnica de productos ISO 5456-2 Dibujos técnicos – Métodos de proyección – Parte 2: Representaciones ortográficas (incluye el símbolo de cono truncado)

• Sitio web educativo que describe los principios de proyección del primer y tercer ángulo — Universidad de Limerick
• Sitio web educativo que describe los principios de proyección del primer y tercer ángulo.
• Imágenes etiquetadas como "Elevation" en Flickr.com
• Método básico de proyección: primer ángulo vs. tercer ángulo