Estrechamiento (ingeniería)

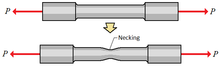
En ingeniería y ciencia de los materiales , el estrechamiento es un modo de deformación por tracción en el que cantidades relativamente grandes de deformación se localizan desproporcionadamente en una pequeña región del material. La disminución prominente resultante en el área de la sección transversal local proporciona la base para el nombre "cuello". Debido a que las deformaciones locales en el cuello son grandes, el estrechamiento a menudo se asocia estrechamente con la fluencia , una forma de deformación plástica asociada con materiales dúctiles , a menudo metales o polímeros . ^[1] Una vez que ha comenzado el estrechamiento, el cuello se convierte en la ubicación exclusiva de fluencia en el material, ya que el área reducida le da al cuello la mayor tensión local .

El estrechamiento resulta de una inestabilidad durante la deformación por tracción cuando el área de la sección transversal de la muestra disminuye en una proporción mayor que la que se endurece por la deformación del material . Armand Considère publicó el criterio básico para el estrechamiento en 1885, en el contexto de la estabilidad de estructuras a gran escala como los puentes. ^[2] Tres conceptos proporcionan el marco para comprender la formación de cuellos.

1. Antes de la deformación, todos los materiales reales presentan heterogeneidades como defectos o variaciones locales en las dimensiones o la composición que provocan fluctuaciones locales en las tensiones y deformaciones . Para determinar la ubicación del cuello incipiente, estas fluctuaciones solo necesitan ser infinitesimales en magnitud.
2. Durante la deformación plástica por tracción, el material disminuye su área de sección transversal debido a la incompresibilidad del flujo plástico (no debido al efecto Poisson , que está vinculado al comportamiento elástico).
3. Durante la deformación plástica por tracción, el material se endurece. La cantidad de endurecimiento varía según el grado de deformación.

Los dos últimos efectos determinan la estabilidad mientras que el primer efecto determina la ubicación del mástil.

Se espera que se produzca inestabilidad (inicio de estrangulamiento) cuando un aumento en la deformación (local) no produce un aumento neto en la carga, F . Esto sucederá cuando

${\displaystyle \Delta F=0}$

Esto conduce a

${\displaystyle {\begin{aligned}&F=A\sigma _{T}\\[4pt]\implies &dF=Ad\sigma _{T}+\sigma _{T}dA=0\\[4pt]\implies &{\frac {d\sigma _{T}}{\sigma _{T}}}=-{\frac {dA}{A}}={\frac {dL}{L}}=d\varepsilon _{T}\\\implies &\sigma _{T}={\frac {d\sigma _{T}}{d\varepsilon _{T}}}\end{aligned}}}$

El subíndice T se utiliza para enfatizar que estas tensiones y deformaciones deben ser valores verdaderos. Por lo tanto, se predice que el estrechamiento comenzará cuando la pendiente de la curva de tensión/deformación verdadera caiga a un valor igual a la tensión verdadera en ese punto.

El estrechamiento es un fenómeno que se produce con frecuencia tanto en metales como en polímeros. Sin embargo, aunque el fenómeno se debe al mismo efecto básico en ambos materiales, tienden a tener diferentes tipos de curva de tensión-deformación (real), de modo que deben considerarse por separado en términos de comportamiento de estrechamiento. En el caso de los metales, la tensión (real) tiende a aumentar de forma monótona con el aumento de la deformación, aunque el gradiente ( velocidad de endurecimiento por deformación ) tiende a disminuir progresivamente. Esto se debe principalmente a una caída progresiva de la movilidad de las dislocaciones , causada por las interacciones entre ellas. En cambio, en el caso de los polímeros, la curva puede ser más compleja. Por ejemplo, en algunos casos el gradiente puede aumentar bruscamente con el aumento de la deformación, debido a que las cadenas de polímeros se alinean a medida que se reorganizan durante la deformación plástica. Esto puede dar lugar a un estrechamiento estable. En los metales no es posible que se produzca ningún efecto de este tipo.

La figura muestra una captura de pantalla de una simulación interactiva disponible en el sitio web educativo DoITPoMS . Se muestra la construcción de una curva de tensión-deformación (real) representada por una expresión analítica simple (Ludwik-Hollomon).

La condición también puede expresarse en términos de la deformación nominal:

${\displaystyle {\begin{aligned}{\frac {d\sigma _{T}}{d\varepsilon _{T}}}&={\frac {d\sigma _{T}}{d\varepsilon _{N}}}{\frac {d\varepsilon _{N}}{d\varepsilon _{T}}}\\[4pt]&={\frac {d\sigma _{T}}{d\varepsilon _{N}}}{\frac {dL/L_{0}}{dL/L}}\\[4pt]&={\frac {d\sigma _{T}}{d\varepsilon _{N}}}{\frac {L}{L_{0}}}\\[4pt]&={\frac {d\sigma _{T}}{d\varepsilon _{N}}}(1+\varepsilon _{\mathrm {N} })\end{alineado}}}$

Por lo tanto, en el punto de inestabilidad:

${\displaystyle \sigma _{T}={\frac {d\sigma _{T}}{d\varepsilon _{N}}}(1+\varepsilon _{N})}$

Por lo tanto, también se puede formular en términos de un gráfico de tensión real frente a deformación nominal. En un gráfico de este tipo, el estrechamiento comenzará donde una línea desde el punto ε _N = –1 forme una tangente a la curva. Esto se muestra en la siguiente figura, que se obtuvo utilizando la misma representación de Ludwik-Hollomon de la relación tensión real – deformación real que la de la figura anterior.

Es importante destacar que la condición también corresponde a un pico (meseta) en el gráfico de tensión nominal – deformación nominal. Esto se puede ver al obtener el gradiente de dicho gráfico al diferenciar la expresión para σ _N con respecto a ε _N .

${\displaystyle {\begin{aligned}\sigma _{N}&={\frac {\sigma _{T}}{1+\varepsilon _{N}}}\\[4pt]\por lo tanto {\frac {d\sigma _{N}}{d\varepsilon _{N}}}&={\frac {d\sigma _{T}}{d\varepsilon _{N}}}{\frac {1}{1+\varepsilon _{N}}}-{\frac {\sigma _{T}}{(1+\varepsilon _{N})^{2}}}\end{aligned}}}$

Sustituyendo el gradiente de tensión nominal-tensión real (al inicio del estrechamiento):

${\displaystyle {\frac {d\sigma_{N}}{d\varepsilon_{N}}}={\frac {\sigma_{T}}{1+\varepsilon_{N}}}{\frac {1}{1+\varepsilon_{N}}}-{\frac {\sigma_{T}}{(1+\varepsilon_{N})^{2}}}=0}$

Esta condición también se puede ver en las dos figuras. Dado que muchas curvas de tensión-deformación se presentan como gráficos nominales, y esta es una condición simple que se puede identificar mediante inspección visual, es en muchos sentidos el criterio más fácil de usar para establecer el inicio del estrechamiento. También corresponde a la "resistencia" ( tensión de tracción máxima ), al menos para los metales que se estrechan (que cubre la mayoría de los metales de "ingeniería"). Por otro lado, el pico en una curva de tensión-deformación nominal es comúnmente una meseta bastante plana, en lugar de un máximo pronunciado, por lo que la evaluación precisa de la deformación al inicio del estrechamiento puede ser difícil. Sin embargo, esta deformación es una indicación significativa de la "ductilidad" del metal, más que la "deformación nominal en la fractura" comúnmente utilizada, que depende de la relación de aspecto de la longitud calibrada de la pieza de prueba de tracción ^[3] ; consulte el artículo sobre ductilidad .

La construcción tangente que se muestra arriba rara vez se utiliza para interpretar las curvas de tensión-deformación de los metales. Sin embargo, es popular para el análisis del estiramiento por tracción de polímeros. ^{[4] [5]} (ya que permite el estudio del régimen de estrangulamiento estable). Se puede observar que, para los polímeros, la deformación se expresa comúnmente como una "ratio de estiramiento", en lugar de una deformación: en este caso, la extrapolación de la tangente se lleva a cabo a un ratio de estiramiento de cero, en lugar de una deformación de -1.

Los gráficos se refieren (arriba) a un material que forma un cuello estable y (abajo) a un material que se deforma de manera homogénea en todas las relaciones de estiramiento.

A medida que avanza la deformación, la inestabilidad geométrica hace que la tensión continúe concentrándose en el cuello hasta que el material se rompa o el material en forma de cuello se endurezca lo suficiente, como lo indica el segundo punto tangente en el diagrama superior, para hacer que otras regiones del material se deformen en su lugar. La cantidad de tensión en el cuello estable se denomina relación de estiramiento natural ^[6] porque está determinada por las características de endurecimiento del material, no por la cantidad de estiramiento impuesto al material. Los polímeros dúctiles a menudo presentan cuellos estables porque la orientación molecular proporciona un mecanismo de endurecimiento que predomina en grandes deformaciones. ^[7]

• Curva de tensión-deformación
• Estrangulamiento de trazas
• Máquina de pruebas universal