Sección transversal (geometría)

En geometría y ciencia , una sección transversal es la intersección no vacía de un cuerpo sólido en el espacio tridimensional con un plano , o su análogo en espacios de dimensiones superiores . Cortar un objeto en rebanadas crea muchas secciones transversales paralelas. El límite de una sección transversal en el espacio tridimensional que es paralelo a dos de los ejes , es decir, paralelo al plano determinado por estos ejes, a veces se denomina línea de contorno ; por ejemplo, si un plano corta a través de montañas de un mapa en relieve paralelo al suelo, el resultado es una línea de contorno en el espacio bidimensional que muestra puntos en la superficie de las montañas de igual elevación .

Parte de una serie sobre
Proyección gráfica
Planar Proyección paralela Proyección ortográfica Proyección isométrica Proyección oblicua Proyección en perspectiva Perspectiva curvilínea Perspectiva inversa
Vistas Vista de pájaro Sección transversal Dibujo en corte Dibujo de vista en despiece Lente ojo de pez Vistas múltiples Panorama Vista desde el punto de vista del gusano Objetivo zoom
Temas Proyección 3D Anamorfosis Axonometría Gráficos de computadora Diseño asistido por ordenador Geometría descriptiva Dibujo de ingeniería Proyección de mapas Plano de imagen Planos (dibujos) Proyección (álgebra lineal) Plano de proyección Geometría proyectiva Estereoscopia Dibujo técnico Longitud real Punto de fuga Gráficos de videojuegos Visualización del tronco truncado
en a mi

En el dibujo técnico, una sección transversal, que es la proyección de un objeto sobre un plano que lo interseca, es una herramienta común que se utiliza para representar la disposición interna de un objeto tridimensional en dos dimensiones. Tradicionalmente, se la raya con un estilo que a menudo indica los tipos de materiales que se utilizan.

Con la tomografía axial computarizada , las computadoras pueden construir secciones transversales a partir de datos de rayos X.

Si un plano interseca un sólido (un objeto tridimensional), entonces la región común al plano y al sólido se llama sección transversal del sólido. ^[1] Un plano que contiene una sección transversal del sólido puede denominarse plano de corte .

La forma de la sección transversal de un sólido puede depender de la orientación del plano de corte con respecto al sólido. Por ejemplo, mientras que todas las secciones transversales de una pelota son discos, ^[2] las secciones transversales de un cubo dependen de cómo se relaciona el plano de corte con el cubo. Si el plano de corte es perpendicular a una línea que une los centros de dos caras opuestas del cubo, la sección transversal será un cuadrado; sin embargo, si el plano de corte es perpendicular a una diagonal del cubo que une vértices opuestos, la sección transversal puede ser un punto, un triángulo o un hexágono.

Un concepto relacionado es el de sección plana , que es la curva de intersección de un plano con una superficie . ^[3] Así, una sección plana es el límite de una sección transversal de un sólido en un plano de corte.

Si una superficie en un espacio tridimensional está definida por una función de dos variables, es decir, z = f ( x , y ) , las secciones planas mediante planos de corte que son paralelos a un plano de coordenadas (un plano determinado por dos ejes de coordenadas) se denominan curvas de nivel o isolíneas . ^[4] Más específicamente, los planos de corte con ecuaciones de la forma z = k (planos paralelos al plano xy ) producen secciones planas que a menudo se denominan líneas de contorno en las áreas de aplicación.

Una sección transversal de un poliedro es un polígono .

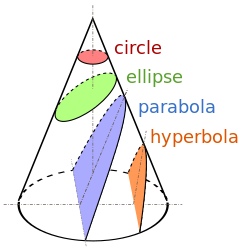
Las secciones cónicas ( círculos , elipses , parábolas e hipérbolas ) son secciones planas de un cono con los planos de corte en distintos ángulos, como se ve en el diagrama de la izquierda.

Cualquier sección transversal que pase por el centro de un elipsoide forma una región elíptica, mientras que las secciones planas correspondientes son elipses en su superficie. Estas degeneran en discos y círculos, respectivamente, cuando los planos de corte son perpendiculares a un eje de simetría. En términos más generales, las secciones planas de una cuádrica son secciones cónicas. ^[5]

Una sección transversal de un cilindro circular recto sólido que se extiende entre dos bases es un disco si la sección transversal es paralela a la base del cilindro, o una región elíptica (ver diagrama a la derecha) si no es paralela ni perpendicular a la base. Si el plano de corte es perpendicular a la base, consiste en un rectángulo (no se muestra) a menos que sea tangente al cilindro, en cuyo caso es un solo segmento de línea .

El término cilindro también puede significar la superficie lateral de un cilindro sólido (ver cilindro (geometría) ). Si se utiliza un cilindro en este sentido, el párrafo anterior se leería de la siguiente manera: Una sección plana de un cilindro circular recto de longitud finita ^[6] es un círculo si el plano de corte es perpendicular al eje de simetría del cilindro, o una elipse si no es ni paralelo ni perpendicular a ese eje. Si el plano de corte es paralelo al eje, la sección plana consta de un par de segmentos de línea paralelos a menos que el plano de corte sea tangente al cilindro, en cuyo caso, la sección plana es un solo segmento de línea.

Se puede utilizar una sección plana para visualizar la derivada parcial de una función con respecto a uno de sus argumentos, como se muestra. Supongamos que z = f ( x , y ) . Al tomar la derivada parcial de f ( x , y ) con respecto a x , se puede tomar una sección plana de la función f en un valor fijo de y para trazar la curva de nivel de z únicamente en función de x ; entonces la derivada parcial con respecto a x es la pendiente del gráfico bidimensional resultante.

Una sección plana de una función de densidad de probabilidad de dos variables aleatorias en la que el plano de corte se encuentra en un valor fijo de una de las variables es una función de densidad condicional de la otra variable (condicionada al valor fijo que define la sección plana). Si, en cambio, se toma la sección plana para un valor fijo de la densidad, el resultado es un contorno de isodensidad . Para la distribución normal , estos contornos son elipses.

En economía , una función de producción f ( x , y ) especifica la producción que se puede producir con varias cantidades x e y de insumos, típicamente mano de obra y capital físico. La función de producción de una empresa o una sociedad se puede representar gráficamente en un espacio tridimensional. Si se toma una sección plana paralela al plano xy , el resultado es una isocuanta que muestra las diversas combinaciones de uso de mano de obra y capital que darían como resultado el nivel de producción dado por la altura de la sección plana. Alternativamente, si se toma una sección plana de la función de producción en un nivel fijo de y —es decir, paralela al plano xz— , entonces el resultado es un gráfico bidimensional que muestra cuánta producción se puede producir en cada uno de los diversos valores de uso x de un insumo combinado con el valor fijo del otro insumo y .

También en economía, una función de utilidad cardinal u ordinal u ( w , v ) da el grado de satisfacción de un consumidor obtenido al consumir cantidades w y v de dos bienes. Si se toma una sección plana de la función de utilidad a una altura dada (nivel de utilidad), el resultado bidimensional es una curva de indiferencia que muestra varias combinaciones alternativas de cantidades consumidas w y v de los dos bienes, todas las cuales dan el nivel de utilidad especificado.

El principio de Cavalieri establece que los sólidos con secciones transversales correspondientes de áreas iguales tienen volúmenes iguales.

El área de la sección transversal ( ) de un objeto cuando se observa desde un ángulo determinado es el área total de la proyección ortográfica del objeto desde ese ángulo. Por ejemplo, un cilindro de altura h y radio r tiene cuando se observa a lo largo de su eje central y cuando se observa desde una dirección ortogonal. Una esfera de radio r tiene cuando se observa desde cualquier ángulo. De manera más genérica, se puede calcular evaluando la siguiente integral de superficie:${\estilo de visualización A'}$${\displaystyle A'=\pi r^{2}}$${\displaystyle A'=2rh}$${\displaystyle A'=\pi r^{2}}$${\estilo de visualización A'}$

${\displaystyle A'=\iint \limits _{\mathrm {arriba} }d\mathbf {A} \cdot \mathbf {\hat {r}} ,}$

donde es el vector unitario que apunta a lo largo de la dirección de visualización hacia el observador, es un elemento de superficie con una normal que apunta hacia afuera, y la integral se toma solo sobre la superficie superior, esa parte de la superficie que es "visible" desde la perspectiva del observador. Para un cuerpo convexo , cada rayo que atraviesa el objeto desde la perspectiva del observador cruza solo dos superficies. Para tales objetos, la integral se puede tomar sobre toda la superficie ( ) tomando el valor absoluto del integrando (de modo que la "parte superior" y la "parte inferior" del objeto no se resten, como lo requeriría el Teorema de divergencia aplicado al campo vectorial constante ) y dividiendo por dos:${\displaystyle \mathbf {\hat {r}} }$${\displaystyle d\mathbf {A}}$${\estilo de visualización A}$${\displaystyle \mathbf {\hat {r}} }$

${\displaystyle A'={\frac {1}{2}}\iint \limits _{A}|d\mathbf {A} \cdot \mathbf {\hat {r}} |}$

En analogía con la sección transversal de un sólido, la sección transversal de un cuerpo n -dimensional en un espacio n -dimensional es la intersección no vacía del cuerpo con un hiperplano (un subespacio ( n − 1) -dimensional). Este concepto se ha utilizado a veces para ayudar a visualizar aspectos de espacios de dimensiones superiores. ^[7] Por ejemplo, si un objeto de cuatro dimensiones pasara a través de nuestro espacio tridimensional, veríamos una sección transversal tridimensional del objeto de cuatro dimensiones. En particular, una esfera de 4 (hiperesfera) que pasa a través del espacio tridimensional aparecería como una esfera de 3 dimensiones que aumentaba hasta un máximo y luego disminuía de tamaño durante la transición. Este objeto dinámico (desde el punto de vista del espacio tridimensional) es una secuencia de secciones transversales de la esfera de 4 dimensiones.

En geología , la estructura del interior de un planeta a menudo se ilustra utilizando un diagrama de una sección transversal del planeta que pasa por el centro del planeta, como en la sección transversal de la Tierra a la derecha.

Las secciones transversales se utilizan a menudo en anatomía para ilustrar la estructura interna de un órgano, como se muestra a la izquierda.

Una sección transversal del tronco de un árbol , como se muestra a la izquierda, revela anillos de crecimiento que pueden usarse para encontrar la edad del árbol y las propiedades temporales de su entorno.

Wikimedia Commons alberga una categoría multimedia sobre Secciones transversales .

• Geometría descriptiva
• Dibujo en despiece
• Proyección gráfica
• Planos (dibujos)
• Calibre de perfil
• Revestimiento de secciones ; representación de materiales
• Plano secante

• Albert, Abraham Adrian (2016) [1949], Geometría analítica de sólidos , Dover, ISBN 978-0-486-81026-3
• Stewart, Ian (2001), Flatterland / como Flatland, sólo que más , Persus Publishing, ISBN 0-7382-0675-X
• Swokowski, Earl W. (1983), Cálculo con geometría analítica (edición alternativa), Prindle, Weber & Schmidt, ISBN 0-87150-341-7