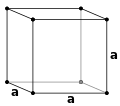
Estructura cristalina

Disposición ordenada de átomos, iones o moléculas en un material cristalino.

En cristalografía , la estructura cristalina es una descripción de la disposición ordenada de átomos , iones o moléculas en un material cristalino . ^[1] Las estructuras ordenadas surgen de la naturaleza intrínseca de las partículas constituyentes para formar patrones simétricos que se repiten a lo largo de las direcciones principales del espacio tridimensional de la materia.

El grupo más pequeño de partículas del material que constituye este patrón repetitivo es la celda unitaria de la estructura. La celda unitaria refleja por completo la simetría y la estructura de todo el cristal, que se construye mediante la traslación repetitiva de la celda unitaria a lo largo de sus ejes principales. Los vectores de traslación definen los nodos de la red de Bravais .

Las longitudes de los ejes/aristas principales de la celda unitaria y los ángulos entre ellos son constantes de red , también llamadas parámetros de red o parámetros de celda . Las propiedades de simetría del cristal se describen mediante el concepto de grupos espaciales . ^[1] Todas las posibles disposiciones simétricas de partículas en el espacio tridimensional pueden describirse mediante 230 grupos espaciales.

La estructura cristalina y la simetría juegan un papel fundamental en la determinación de muchas propiedades físicas, como la escisión , la estructura de la banda electrónica y la transparencia óptica .

Celda unitaria

La estructura cristalina se describe en términos de la geometría de la disposición de las partículas en las celdas unitarias. La celda unitaria se define como la unidad repetitiva más pequeña que tiene la simetría completa de la estructura cristalina. ^[2] La geometría de la celda unitaria se define como un paralelepípedo , que proporciona seis parámetros de red tomados como las longitudes de los bordes de la celda ( a , b , c ) y los ángulos entre ellos ( α , β , γ ). Las posiciones de las partículas dentro de la celda unitaria se describen mediante las coordenadas fraccionarias ( x _i , y _i , z _i ) a lo largo de los bordes de la celda, medidas desde un punto de referencia. Por lo tanto, solo es necesario informar las coordenadas de un subconjunto asimétrico más pequeño de partículas, llamado unidad asimétrica cristalográfica. La unidad asimétrica puede elegirse de modo que ocupe el espacio físico más pequeño, lo que significa que no todas las partículas necesitan estar ubicadas físicamente dentro de los límites dados por los parámetros de red. Todas las demás partículas de la celda unitaria se generan mediante las operaciones de simetría que caracterizan la simetría de la celda unitaria. El conjunto de operaciones de simetría de la celda unitaria se expresa formalmente como el grupo espacial de la estructura cristalina. ^[3]

Cúbica simple (P)
Cúbica centrada en el cuerpo (I)
Cúbica centrada en las caras (F)

Índices de Miller

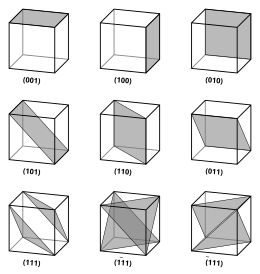
Los vectores y planos de una red cristalina se describen mediante la notación de índice de Miller de tres valores . Esta sintaxis utiliza los índices h , k y ℓ como parámetros direccionales. ^[4]

Por definición, la sintaxis ( hkℓ ) denota un plano que intercepta los tres puntos a ₁ / h , a ₂ / k y a ₃ / ℓ , o algún múltiplo de los mismos. Es decir, los índices de Miller son proporcionales a las inversas de las intersecciones del plano con la celda unitaria (en la base de los vectores reticulares). Si uno o más de los índices es cero, significa que los planos no intersecan ese eje (es decir, la intersección está "en el infinito"). Un plano que contiene un eje de coordenadas se traslada de modo que ya no contenga ese eje antes de que se determinen sus índices de Miller. Los índices de Miller para un plano son números enteros sin factores comunes. Los índices negativos se indican con barras horizontales, como en (1 2 3). En un sistema de coordenadas ortogonales para una celda cúbica, los índices de Miller de un plano son los componentes cartesianos de un vector normal al plano.

Considerando solo los planos ( hkℓ ) que intersecan uno o más puntos de la red (los planos de la red ), la distancia d entre planos de la red adyacentes está relacionada con el vector de red recíproco (más corto) ortogonal a los planos mediante la fórmula

d={\frac {2\pi }{|\mathbf {g} _{hk\ell }|}}

Planos y direcciones

Las direcciones cristalográficas son líneas geométricas que unen nodos ( átomos , iones o moléculas ) de un cristal. Asimismo, los planos cristalográficos son planos geométricos que unen nodos. Algunas direcciones y planos tienen una mayor densidad de nodos. Estos planos de alta densidad tienen una influencia en el comportamiento del cristal de la siguiente manera: ^[1]

Propiedades ópticas : El índice de refracción está directamente relacionado con la densidad (o fluctuaciones periódicas de densidad).
Adsorción y reactividad : La adsorción física y las reacciones químicas ocurren en la superficie de los átomos o moléculas o cerca de ellos. Por lo tanto, estos fenómenos son sensibles a la densidad de nodos.
Tensión superficial : La condensación de un material hace que los átomos, iones o moléculas sean más estables si están rodeados de otras especies similares. La tensión superficial de una interfase varía en función de la densidad de la superficie.

Defectos microestructurales : Los poros y los cristalitos tienden a tener límites de grano rectos siguiendo planos de mayor densidad.
Escisión : esto suele ocurrir preferentemente en paralelo a los planos de mayor densidad.
Deformación plástica : el deslizamiento de la dislocación se produce preferentemente en paralelo a los planos de mayor densidad. La perturbación transportada por la dislocación ( vector de Burgers ) se produce en una dirección densa. El desplazamiento de un nodo en una dirección más densa requiere una menor distorsión de la red cristalina.

Algunas direcciones y planos se definen por la simetría del sistema cristalino. En los sistemas monoclínicos, trigonales, tetragonales y hexagonales hay un único eje (a veces llamado eje principal ) que tiene mayor simetría rotacional que los otros dos ejes. El plano basal es el plano perpendicular al eje principal en estos sistemas cristalinos. En los sistemas cristalinos triclínicos, ortorrómbicos y cúbicos, la designación del eje es arbitraria y no hay eje principal.

Estructuras cúbicas

Para el caso especial de cristales cúbicos simples, los vectores de red son ortogonales y de igual longitud (usualmente denotados como a ); lo mismo ocurre con la red recíproca. Por lo tanto, en este caso común, los índices de Miller ( ℓmn ) y [ ℓmn ] simplemente denotan normales/direcciones en coordenadas cartesianas . Para cristales cúbicos con constante de red a , el espaciamiento d entre planos de red adyacentes (ℓmn) es (de arriba):

d_{\ell mn}={\frac {a}{\sqrt {\ell ^{2}+m^{2}+n^{2}}}}

Debido a la simetría de los cristales cúbicos, es posible cambiar el lugar y el signo de los números enteros y tener direcciones y planos equivalentes:

Las coordenadas entre corchetes angulares, como ⟨100⟩, denotan una familia de direcciones que son equivalentes debido a operaciones de simetría, como [100], [010], [001] o el negativo de cualquiera de esas direcciones.
Las coordenadas entre llaves o corchetes como {100} denotan una familia de normales del plano que son equivalentes debido a operaciones de simetría, de forma muy similar a como los corchetes angulares denotan una familia de direcciones.

En el caso de las redes cúbicas centradas en las caras (fcc) y cúbicas centradas en el cuerpo (bcc), los vectores reticulares primitivos no son ortogonales. Sin embargo, en estos casos los índices de Miller se definen convencionalmente en relación con los vectores reticulares de la supercelda cúbica y, por lo tanto, son simplemente las direcciones cartesianas .

Espaciamiento interplanar

El espaciamiento d entre planos reticulares adyacentes ( hkℓ ) viene dado por: ^[5]^[6]

Cúbico:
${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}+\ell ^{2}}{a^{2}}}$
Tetragonal:
${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}}{a^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$
Hexagonal:
${\frac {1}{d^{2}}}={\frac {4}{3}}\left({\frac {h^{2}+hk+k^{2}}{a^{2}}}\right)+{\frac {\ell ^{2}}{c^{2}}}$
Romboédrico ( configuración primitiva ):
${\frac {1}{d^{2}}}={\frac {(h^{2}+k^{2}+\ell ^{2})\sin ^{2}\alpha +2(hk+k\ell +h\ell )(\cos ^{2}\alpha -\cos \alpha )}{a^{2}(1-3\cos ^{2}\alpha +2\cos ^{3}\alpha )}}$
Ortorrómbico:
${\frac {1}{d^{2}}}={\frac {h^{2}}{a^{2}}}+{\frac {k^{2}}{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$
Monoclínico:
${\frac {1}{d^{2}}}=\left({\frac {h^{2}}{a^{2}}}+{\frac {k^{2}\sin ^{2}\beta }{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}-{\frac {2h\ell \cos \beta }{ac}}\right)\csc ^{2}\beta$
Triclínica:
${\frac {1}{d^{2}}}={\frac {{\frac {h^{2}}{a^{2}}}\sin ^{2}\alpha +{ \frac {k^{2}}{b^{2}}}\sin ^{2}\beta +{\frac {\ell ^{2}}{c^{2}}}\sin ^{2 }\gamma +{\frac {2k\ell }{bc}}(\cos \beta \cos \gamma -\cos \alpha )+{\frac {2h\ell }{ac}}(\cos \gamma \ cos \alpha -\cos \beta )+{\frac {2hk}{ab}}(\cos \alpha \cos \beta -\cos \gamma )}{1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$

Clasificación por simetría

La propiedad que define a un cristal es su simetría inherente. La realización de ciertas operaciones de simetría en la red cristalina la deja inalterada. Todos los cristales tienen simetría traslacional en tres direcciones, pero algunos tienen también otros elementos de simetría. Por ejemplo, rotar el cristal 180° sobre un eje determinado puede dar como resultado una configuración atómica idéntica a la configuración original; el cristal tiene simetría rotacional doble sobre este eje. Además de la simetría rotacional, un cristal puede tener simetría en forma de planos especulares, y también las llamadas simetrías compuestas, que son una combinación de traslación y rotación o simetrías especulares. Se logra una clasificación completa de un cristal cuando se identifican todas las simetrías inherentes del cristal. ^[7]

Sistemas de celosía

Los sistemas reticulares son una agrupación de estructuras cristalinas según los grupos puntuales de su red. Todos los cristales pertenecen a uno de los siete sistemas reticulares. Están relacionados con los siete sistemas cristalinos , pero no son iguales .

Descripción general de los sistemas de celosía más comunes
Familia de cristal	Sistema de celosía	Grupo de puntos ( notación de Schönflies )	14 celosías de Bravais
Familia de cristal	Sistema de celosía	Grupo de puntos ( notación de Schönflies )	Primitivo (P)	Centrado en la base (S)	Centrado en el cuerpo (I)	Centrado en la cara (F)
Triclínica (a)		C _yo	aP
Monoclínico (m)		C _{2 horas}	parlamentario	EM
Ortorrómbico (o)		D 2 _horas	deo	sistema operativo	yo	de
Tetragonal (t)		D _{4 horas}	tP		yo
Hexagonal (h)	Romboédrico	D _3d	hora
Hexagonal (h)	Hexagonal	D _{6 horas}	persona de edad avanzada
Cúbico (c)		Oh	cP		yo	cF

El sistema más simétrico, el cúbico o isométrico, tiene la simetría de un cubo , es decir, presenta cuatro ejes de rotación triples orientados a 109,5° (el ángulo tetraédrico ) entre sí. Estos ejes triples se encuentran a lo largo de las diagonales del cuerpo del cubo. Los otros seis sistemas reticulares son el hexagonal , el tetragonal , el romboédrico (a menudo confundido con el sistema cristalino trigonal ), el ortorrómbico , el monoclínico y el triclínico .

Celosías de Bravais

Las redes de Bravais , también denominadas redes espaciales , describen la disposición geométrica de los puntos de la red ^[4] y, por lo tanto, la simetría traslacional del cristal. Las tres dimensiones del espacio proporcionan 14 redes de Bravais distintas que describen la simetría traslacional. Todos los materiales cristalinos reconocidos hoy en día, sin incluir los cuasicristales , encajan en una de estas disposiciones. Las catorce redes tridimensionales, clasificadas por sistema de red, se muestran arriba.

La estructura cristalina está formada por el mismo grupo de átomos, la base , situados alrededor de cada uno de los puntos de la red. Por tanto, este grupo de átomos se repite indefinidamente en tres dimensiones según la disposición de una de las redes de Bravais. La rotación característica y las simetrías especulares de la celda unitaria se describen mediante su grupo puntual cristalográfico .

Sistemas de cristal

Un sistema cristalino es un conjunto de grupos puntuales en el que los propios grupos puntuales y sus correspondientes grupos espaciales se asignan a un sistema reticular. De los 32 grupos puntuales que existen en tres dimensiones, la mayoría se asignan a un solo sistema reticular, en cuyo caso el sistema cristalino y el sistema reticular tienen el mismo nombre. Sin embargo, cinco grupos puntuales se asignan a dos sistemas reticulares, romboédrico y hexagonal, porque ambos sistemas reticulares presentan una simetría rotacional triple. Estos grupos puntuales se asignan al sistema cristalino trigonal.

Descripción general de los sistemas cristalinos
Familia de cristal	Sistema de cristal	Grupo de puntos / Clase de cristal	Moscas de Schön	Simetría de puntos	Orden	Grupo abstracto
triclínico		pediatra	C ₁	polar enantiomórfico	1	trivial $\mathbb {Z} _ {1}$
triclínico		pinacoidal	Ci ₍ S ₂ )	centrosimétrico	2	cíclico $\mathbb {Z} _ {2}$
monoclínico		esfenoidal	C ₂	polar enantiomórfico	2	cíclico $\mathbb {Z} _ {2}$
		domático	Cs ( C _1h₎	polar	2	cíclico $\mathbb {Z} _ {2}$
		prismático	C _{2 horas}	centrosimétrico	4	Klein cuatro $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
ortorrómbico		rómbico-disfenoidal	D2 (V ₎	enantiomórfico	4	Klein cuatro $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		rómbico- piramidal	C2v	polar	4	Klein cuatro $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		rómbico- bipiramidal	D _2h ( _Vh )	centrosimétrico	8	$\mathbb {V} \times \mathbb {Z} _{2}$
tetragonal		tetragonal-piramidal	C ₄	polar enantiomórfico	4	cíclico $\mathbb {Z} _ {4}$
		tetragonal-diesfenoidal	S ₄	no centrosimétrico	4	cíclico $\mathbb {Z} _ {4}$
		tetragonal-bipiramidal	C _{4 horas}	centrosimétrico	8	$\mathbb {Z} _{4}\times \mathbb {Z} _{2}$
		tetragonal-trapezoédrico	D4	enantiomórfico	8	diedro $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		piramidal ditetragonal	C _4v	polar	8	diedro $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		tetragonal-escalenoédrico	D _2d ( _Vd )	no centrosimétrico	8	diedro $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		ditetragonal-bipiramidal	D _{4 horas}	centrosimétrico	16	$\mathbb {D} _{8}\times \mathbb {Z} _{2}$
hexagonal	trigonal	piramidal trigonal	C ₃	polar enantiomórfico	3	cíclico $\mathbb {Z} _ {3}$
		romboédrico	C3i ( _S6 )	centrosimétrico	6	cíclico $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		Trigonal-trapezoédrico	D3	enantiomórfico	6	diedro $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		piramidal ditrigonal	C _3v	polar	6	diedro $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		ditrigonal-escalenoédrico	D _3d	centrosimétrico	12	diedro $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
	hexagonal	piramidal hexagonal	C ₆	polar enantiomórfico	6	cíclico $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		trigonal-bipiramidal	C _{3 horas}	no centrosimétrico	6	cíclico $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		hexagonal-bipiramidal	C _{6 horas}	centrosimétrico	12	$\mathbb {Z} _{6}\times \mathbb {Z} _{2}$
		trapezoédrico hexagonal	D6	enantiomórfico	12	diedro $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		piramidal dihexagonal	C _6v	polar	12	diedro $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		ditrigonal-bipiramidal	D 3 _horas	no centrosimétrico	12	diedro $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		dihexagonal-bipiramidal	D _{6 horas}	centrosimétrico	24	$\mathbb {D} _{12}\times \mathbb {Z} _{2}$
cúbico		tetartoidal	yo	enantiomórfico	12	alterno $\mathbb {A} _{4}$
		diploide	El	centrosimétrico	24	$\mathbb {A} _{4}\times \mathbb {Z} _{2}$
		giroideo	Oh	enantiomórfico	24	simétrico $\mathbb {S} _{4}$
		hextetraédrico	T.D.	no centrosimétrico	24	simétrico $\mathbb {S} _{4}$
		hexoctaédrico	Oh	centrosimétrico	48	$\mathbb {S} _{4}\times \mathbb {Z} _{2}$

En total hay siete sistemas cristalinos: triclínico, monoclínico, ortorrómbico, tetragonal, trigonal, hexagonal y cúbico.

Grupos de puntos

El grupo puntual cristalográfico o clase cristalina es el grupo matemático que comprende las operaciones de simetría que dejan al menos un punto inalterado y que dejan inalterada la apariencia de la estructura cristalina. Estas operaciones de simetría incluyen

Reflexión , que refleja la estructura a través de un plano de reflexión.
Rotación , que hace girar la estructura una porción específica de un círculo alrededor de un eje de rotación.
Inversión , que cambia el signo de la coordenada de cada punto con respecto a un centro de simetría o punto de inversión.
Rotación impropia , que consiste en una rotación alrededor de un eje seguida de una inversión.

Los ejes de rotación (propios e impropios), los planos de reflexión y los centros de simetría se denominan colectivamente elementos de simetría . Existen 32 clases de cristales posibles. Cada una de ellas puede clasificarse en uno de los siete sistemas cristalinos.

Grupos espaciales

Además de las operaciones del grupo puntual, el grupo espacial de la estructura cristalina contiene operaciones de simetría traslacional, entre las que se incluyen:

Traslaciones puras , que mueven un punto a lo largo de un vector
Ejes de tornillo , que giran un punto alrededor de un eje mientras se trasladan paralelos al eje. ^[8]
Planos de deslizamiento , que reflejan un punto a través de un plano mientras lo trasladan paralelo al plano. ^[8]

Hay 230 grupos espaciales distintos.

Coordinación atómica

Considerando la disposición de los átomos entre sí, sus números de coordinación, distancias interatómicas, tipos de enlace, etc., es posible formar una visión general de las estructuras y formas alternativas de visualizarlas. ^[9]

Embalaje compacto

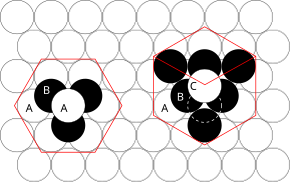
Los principios implicados se pueden entender considerando la forma más eficiente de agrupar esferas de igual tamaño y apilar planos atómicos muy compactos en tres dimensiones. Por ejemplo, si el plano A se encuentra debajo del plano B, hay dos formas posibles de colocar un átomo adicional sobre la capa B. Si se colocara una capa adicional directamente sobre el plano A, esto daría lugar a la siguiente serie:

... ABABAB ...

Esta disposición de átomos en una estructura cristalina se conoce como empaquetamiento compacto hexagonal (hcp) .

Sin embargo, si los tres planos están escalonados entre sí y no es hasta que la cuarta capa se posiciona directamente sobre el plano A que se repite la secuencia, entonces surge la siguiente secuencia:

... ABCABCABC ...

Este tipo de disposición estructural se conoce como empaquetamiento cúbico compacto (ccp) .

La celda unitaria de una disposición ccp de átomos es la celda unitaria cúbica centrada en las caras (fcc). Esto no es inmediatamente obvio ya que las capas compactas son paralelas a los planos {111} de la celda unitaria fcc. Hay cuatro orientaciones diferentes de las capas compactas.

APF y CN

Una característica importante de una estructura cristalina es su factor de empaquetamiento atómico (FPA). Este se calcula suponiendo que todos los átomos son esferas idénticas, con un radio lo suficientemente grande como para que cada esfera se apoye en la siguiente. El factor de empaquetamiento atómico es la proporción de espacio que ocupan estas esferas, que se puede calcular calculando el volumen total de las esferas y dividiéndolo por el volumen de la celda de la siguiente manera:

\mathrm {APF} ={\frac {N_{\mathrm {particle} }V_{\mathrm {particle} }}{V_{\text{unit cell}}}}

Otra característica importante de una estructura cristalina es su número de coordinación (CN), que es el número de vecinos más próximos a un átomo central en la estructura.

A continuación se muestran los APF y CN de las estructuras cristalinas más comunes:

Estructura cristalina	Factor de empaquetamiento atómico	Número de coordinación ( Geometría )
Diamante cúbico	0,34	4 ( Tetraedro )
Cúbico simple	0,52 ^[10]	6 ( Octaedro )
Cúbica centrada en el cuerpo (BCC)	0,68 ^[10]	8 ( Cubo )
Cúbica centrada en las caras (FCC)	0,74 ^[10]	12 ( Cuboctaedro )
Hexagonal compacto (HCP)	0,74 ^[10]	12 ( Ortobicúpula triangular )

La eficiencia de empaquetamiento del 74% del FCC y HCP es la densidad máxima posible en celdas unitarias construidas con esferas de un solo tamaño.

Sitios intersticiales

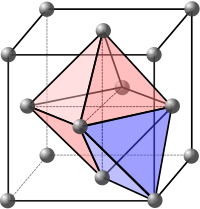
Los sitios intersticiales son los espacios vacíos entre los átomos en la red cristalina. Estos espacios pueden llenarse con iones con cargas opuestas para formar estructuras de múltiples elementos. También pueden llenarse con átomos de impurezas o autointersticiales para formar defectos intersticiales .

Defectos e impurezas

Los cristales reales presentan defectos o irregularidades en las disposiciones ideales descritas anteriormente y son estos defectos los que determinan críticamente muchas de las propiedades eléctricas y mecánicas de los materiales reales.

Impurezas

Cuando un átomo sustituye a uno de los componentes atómicos principales dentro de la estructura cristalina, puede producirse una alteración de las propiedades eléctricas y térmicas del material. ^[11] Las impurezas también pueden manifestarse como impurezas de espín electrónico en ciertos materiales. La investigación sobre impurezas magnéticas demuestra que la alteración sustancial de ciertas propiedades, como el calor específico, puede verse afectada por pequeñas concentraciones de una impureza, como por ejemplo las impurezas en aleaciones ferromagnéticas semiconductoras pueden dar lugar a propiedades diferentes, como se predijo por primera vez a finales de los años 1960. ^[12]^[13]

Dislocaciones

Las dislocaciones en una red cristalina son defectos lineales que están asociados con campos de tensión locales. Las dislocaciones permiten el corte con una tensión menor que la necesaria para una estructura cristalina perfecta. ^[14] Los campos de tensión locales dan lugar a interacciones entre las dislocaciones que luego dan lugar al endurecimiento por deformación o al trabajo en frío .

Límites de grano

Los límites de grano son interfaces donde se encuentran cristales de diferentes orientaciones. ^[4] Un límite de grano es una interfaz monofásica, con cristales a cada lado del límite que son idénticos excepto en la orientación. El término "límite de cristalito" se utiliza a veces, aunque raramente. Las áreas de límite de grano contienen aquellos átomos que han sido perturbados de sus sitios reticulares originales, dislocaciones e impurezas que han migrado al límite de grano de menor energía.

Si consideramos geométricamente un límite de grano como una interfaz de un único cristal cortado en dos partes, una de las cuales está rotada, observamos que se requieren cinco variables para definir un límite de grano. Los dos primeros números provienen del vector unitario que especifica un eje de rotación. El tercer número designa el ángulo de rotación del grano. Los dos últimos números especifican el plano del límite de grano (o un vector unitario que es normal a este plano). ^[9]

Los límites de grano interrumpen el movimiento de las dislocaciones a través de un material, por lo que reducir el tamaño de los cristales es una forma común de mejorar la resistencia, como se describe en la relación Hall-Petch . Dado que los límites de grano son defectos en la estructura cristalina, tienden a disminuir la conductividad eléctrica y térmica del material. La alta energía interfacial y la unión relativamente débil en la mayoría de los límites de grano a menudo los convierte en sitios preferidos para el inicio de la corrosión y para la precipitación de nuevas fases del sólido. También son importantes para muchos de los mecanismos de fluencia . ^[9]

Los límites de grano tienen en general sólo unos pocos nanómetros de ancho. En los materiales comunes, los cristalitos son lo suficientemente grandes como para que los límites de grano representen una pequeña fracción del material. Sin embargo, se pueden lograr tamaños de grano muy pequeños. En los sólidos nanocristalinos, los límites de grano se convierten en una fracción de volumen significativa del material, con profundos efectos en propiedades tales como la difusión y la plasticidad . En el límite de los cristalitos pequeños, a medida que la fracción de volumen de los límites de grano se acerca al 100%, el material deja de tener cualquier carácter cristalino y, por lo tanto, se convierte en un sólido amorfo . ^[9]

Predicción de la estructura

La dificultad de predecir estructuras cristalinas estables basándose únicamente en el conocimiento de la composición química ha sido durante mucho tiempo un obstáculo en el camino hacia el diseño de materiales totalmente computacional. Ahora, con algoritmos más potentes y computación de alto rendimiento, se pueden predecir estructuras de complejidad media utilizando enfoques como algoritmos evolutivos , muestreo aleatorio o metadinámica.

Las estructuras cristalinas de los sólidos iónicos simples (por ejemplo, NaCl o sal de mesa) se han racionalizado desde hace mucho tiempo en términos de las reglas de Pauling , establecidas por primera vez en 1929 por Linus Pauling , a quien muchos se refieren desde entonces como el "padre del enlace químico". ^[15] Pauling también consideró la naturaleza de las fuerzas interatómicas en los metales y concluyó que aproximadamente la mitad de los cinco orbitales d en los metales de transición están involucrados en el enlace, y los orbitales d no enlazantes restantes son responsables de las propiedades magnéticas. Por lo tanto, Pauling pudo correlacionar el número de orbitales d en la formación de enlaces con la longitud del enlace, así como con muchas de las propiedades físicas de la sustancia. Posteriormente introdujo el orbital metálico, un orbital adicional necesario para permitir la resonancia sin inhibiciones de los enlaces de valencia entre varias estructuras electrónicas. ^[16]

En la teoría del enlace de valencia resonante , los factores que determinan la elección de una de las estructuras cristalinas alternativas de un metal o compuesto intermetálico giran en torno a la energía de resonancia de los enlaces entre las posiciones interatómicas. Está claro que algunos modos de resonancia harían contribuciones mayores (serían más estables mecánicamente que otros), y que en particular una simple relación entre el número de enlaces y el número de posiciones sería excepcional. El principio resultante es que una estabilidad especial está asociada con las relaciones más simples o "números de enlace": 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 , etc. La elección de la estructura y el valor de la relación axial (que determina las longitudes de enlace relativas) son, por tanto, el resultado del esfuerzo de un átomo por utilizar su valencia en la formación de enlaces estables con números de enlace fraccionarios simples. ^[17]^[18]

Después de postular una correlación directa entre la concentración de electrones y la estructura cristalina en aleaciones de fase beta, Hume-Rothery analizó las tendencias en los puntos de fusión, compresibilidades y longitudes de enlace como una función del número de grupo en la tabla periódica con el fin de establecer un sistema de valencias de los elementos de transición en el estado metálico. Este tratamiento, por tanto, enfatizó la creciente fuerza de enlace como una función del número de grupo. ^[19] La operación de fuerzas direccionales se enfatizó en un artículo sobre la relación entre los híbridos de enlace y las estructuras metálicas. La correlación resultante entre las estructuras electrónicas y cristalinas se resume en un solo parámetro, el peso de los electrones d por orbital metálico hibridado. El "peso d" se calcula en 0,5, 0,7 y 0,9 para las estructuras fcc, hcp y bcc respectivamente. La relación entre los electrones d y la estructura cristalina se hace evidente. ^[20]

En las predicciones/simulaciones de estructuras cristalinas, se suele aplicar la periodicidad, ya que se imagina que el sistema es ilimitado en todas las direcciones. Partiendo de una estructura triclínica sin ninguna propiedad de simetría adicional asumida, el sistema puede ser impulsado a mostrar algunas propiedades de simetría adicionales aplicando la Segunda Ley de Newton a las partículas en la celda unitaria y una ecuación dinámica desarrollada recientemente para los vectores de período del sistema ^[21] (parámetros de red que incluyen ángulos), incluso si el sistema está sujeto a tensión externa.

Polimorfismo

El polimorfismo es la aparición de múltiples formas cristalinas de un material. Se encuentra en muchos materiales cristalinos, incluidos polímeros , minerales y metales . Según las reglas de equilibrio de fases de Gibbs, estas fases cristalinas únicas dependen de variables intensivas como la presión y la temperatura. El polimorfismo está relacionado con la alotropía , que se refiere a los sólidos elementales . La morfología completa de un material se describe por el polimorfismo y otras variables como el hábito cristalino , la fracción amorfa o los defectos cristalográficos . Los polimorfos tienen diferentes estabilidades y pueden transformarse espontánea e irreversiblemente de una forma metaestable (o forma termodinámicamente inestable) a la forma estable a una temperatura particular. ^[22] También exhiben diferentes puntos de fusión , solubilidades y patrones de difracción de rayos X.

Un buen ejemplo de esto es la forma de cuarzo del dióxido de silicio , o SiO ₂ . En la gran mayoría de los silicatos , el átomo de Si muestra una coordinación tetraédrica por 4 oxígenos. Todas las formas cristalinas excepto una involucran unidades tetraédricas {SiO ₄ } unidas entre sí por vértices compartidos en diferentes disposiciones. En diferentes minerales, los tetraedros muestran diferentes grados de interconexión y polimerización. Por ejemplo, se presentan individualmente, unidos en pares, en grupos finitos más grandes que incluyen anillos, en cadenas, cadenas dobles, láminas y marcos tridimensionales. Los minerales se clasifican en grupos basados en estas estructuras. En cada una de las 7 formas cristalinas termodinámicamente estables o polimorfos del cuarzo cristalino, solo 2 de cada 4 de cada uno de los bordes de los tetraedros {SiO ₄ } se comparten con otros, lo que produce la fórmula química neta para la sílice: SiO ₂ .

Otro ejemplo es el estaño elemental (Sn), que es maleable cerca de temperaturas ambiente pero es frágil cuando se enfría. Este cambio en las propiedades mecánicas se debe a la existencia de sus dos alótropos principales , α- y β-estaño. Los dos alótropos que se encuentran a presión y temperatura normales, α-estaño y β-estaño, se conocen más comúnmente como estaño gris y estaño blanco respectivamente. Dos alótropos más, γ y σ, existen a temperaturas superiores a 161 °C y presiones superiores a varios GPa. ^[23] El estaño blanco es metálico y es la forma cristalina estable a temperatura ambiente o superior. Por debajo de 13,2 °C, el estaño existe en forma gris, que tiene una estructura cristalina cúbica de diamante , similar al diamante , el silicio o el germanio . El estaño gris no tiene propiedades metálicas en absoluto, es un material en polvo gris opaco y tiene pocos usos, aparte de unas pocas aplicaciones especializadas en semiconductores . ^[24] Aunque la temperatura de transformación α–β del estaño es nominalmente 13,2 °C, las impurezas (por ejemplo, Al, Zn, etc.) reducen la temperatura de transición muy por debajo de 0 °C, y tras la adición de Sb o Bi la transformación puede no ocurrir en absoluto. ^[25]

Propiedades físicas

Veinte de las 32 clases de cristales son piezoeléctricos , y los cristales que pertenecen a una de estas clases (grupos puntuales) muestran piezoelectricidad . Todas las clases piezoeléctricas carecen de simetría de inversión . Cualquier material desarrolla una polarización dieléctrica cuando se le aplica un campo eléctrico, pero una sustancia que tiene una separación de carga natural de este tipo incluso en ausencia de un campo se denomina material polar. Si un material es polar o no está determinado únicamente por su estructura cristalina. Solo 10 de los 32 grupos puntuales son polares . Todos los cristales polares son piroeléctricos , por lo que las 10 clases de cristales polares a veces se denominan clases piroeléctricas.

Existen algunas estructuras cristalinas, en particular la estructura de perovskita , que presentan un comportamiento ferroeléctrico . Esto es análogo al ferromagnetismo , en el sentido de que, en ausencia de un campo eléctrico durante la producción, el cristal ferroeléctrico no exhibe una polarización. Al aplicar un campo eléctrico de magnitud suficiente, el cristal se polariza permanentemente. Esta polarización se puede revertir mediante una contracarga suficientemente grande, de la misma manera que se puede revertir un ferroimán. Sin embargo, aunque se denominan ferroeléctricos, el efecto se debe a la estructura cristalina (no a la presencia de un metal ferroso).

Algunos ejemplos de estructuras cristalinas

CH3COONa.3H2O
C2H5ONa
Cloruro de potasio
CaF2
TiO2
NaCl
β-cuarzo (SiO ₂ )
Rubí

Véase también

Zona de Brillouin : una celda primitiva en la red espacial recíproca de un cristal
Ingeniería de cristales
Crecimiento de cristales : una etapa importante del proceso de cristalización
Base de datos cristalográfica
Coordenadas fraccionarias
Fases de Frank-Kasper
Notación de Hermann-Mauguin : una notación para representar la simetría en grupos de puntos, grupos de planos y grupos espaciales.
Crecimiento de cristales mediante pedestal calentado por láser
Cristal líquido : un estado de la materia con propiedades tanto de líquidos como de cristales convencionales.
Función de Patterson : función utilizada para resolver el problema de fase en cristalografía de rayos X
Tabla periódica (estructura cristalina) : (para elementos que son sólidos a temperatura y presión estándar) proporciona la estructura cristalina de las formas más estables desde el punto de vista termodinámico en esas condiciones. En todos los demás casos, la estructura indicada corresponde al elemento en su punto de fusión.
Celda primitiva : unidad repetitiva formada por los vectores que abarcan los puntos de una red.
Cristal semilla : un pequeño trozo de un solo cristal que se utiliza para iniciar el crecimiento de un cristal más grande.
Celda de Wigner-Seitz : una celda primitiva de una red cristalina con descomposición de Voronoi aplicada

Referencias

^ abc Hook, JR; Hall, HE (2010). Física del estado sólido . Manchester Physics Series (2.ª ed.). John Wiley & Sons. ISBN 9780471928041.
^ West, Anthony R. (1999). Química básica del estado sólido (2.ª ed.). Wiley. pág. 1. ISBN 978-0-471-98756-7.
^ Tablas internacionales de cristalografía (2006). Volumen A, Simetría de grupos espaciales.
^ Enciclopedia abc de física (segunda edición), RG Lerner , GL Trigg, editores VHC, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
^ "4. Redes directas y recíprocas". CSIC Departamento de Cristalografía y Biología Estructural . 6 de abril de 2017 . Consultado el 18 de mayo de 2017 .
^ Edington, JW (1975). Difracción de electrones en el microscopio electrónico . doi :10.1007/978-1-349-02595-4. ISBN 978-0-333-18292-5.
^ Ashcroft, N .; Mermin, D. (1976). "Capítulo 7". Física del estado sólido . Brooks/Cole (Thomson Learning, Inc.). ISBN 978-0030493461.
^ de Donald E. Sands (1994). "§4-2 Ejes de tornillo y §4-3 Planos de deslizamiento". Introducción a la cristalografía (reimpresión de WA Benjamin corregida, edición de 1975). Courier-Dover. págs. 70–71. ISBN 978-0486678399.
^ abcd Parker, CB, ed. (1994). Enciclopedia de Física McGraw Hill (2.ª ed.). McGraw-Hill. ISBN 978-0070514003.
^ abcd Ellis, Arthur B.; et al. (1995). Teaching General Chemistry: A Materials Science Companion (Enseñanza de la química general: un manual de ciencia de los materiales) (3.ª ed.). Washington, DC: American Chemical Society. ISBN 084122725X.
^ Kallay, Nikola (2000). Dinámica interfacial. CRC Press. ISBN 978-0824700065.
^ Hogan, CM (1969). "Densidad de estados de una aleación ferromagnética aislante". Physical Review . 188 (2): 870–874. Código Bibliográfico :1969PhRv..188..870H. doi :10.1103/PhysRev.188.870.
^ Zhang, XY; Suhl, H (1985). "Duplicaciones de períodos relacionados con ondas de espín y caos bajo bombeo transversal". Physical Review A . 32 (4): 2530–2533. Bibcode :1985PhRvA..32.2530Z. doi :10.1103/PhysRevA.32.2530. PMID 9896377.
^ Courtney, Thomas (2000). Comportamiento mecánico de los materiales . Long Grove, IL: Waveland Press. pág. 85. ISBN 978-1-57766-425-3.
^ L. Pauling (1929). "Los principios que determinan la estructura de los cristales iónicos complejos". J. Am. Chem. Soc. 51 (4): 1010–1026. doi :10.1021/ja01379a006.
^ Pauling, Linus (1938). "La naturaleza de las fuerzas interatómicas en los metales". Physical Review . 54 (11): 899–904. Código Bibliográfico :1938PhRv...54..899P. doi :10.1103/PhysRev.54.899.
^ Pauling, Linus (1947). "Radios atómicos y distancias interatómicas en metales". Revista de la Sociedad Química Americana . 69 (3): 542–553. doi :10.1021/ja01195a024.
^ Pauling, L. (1949). "Una teoría de enlace de valencia resonante de metales y compuestos intermetálicos". Actas de la Royal Society A . 196 (1046): 343–362. Bibcode :1949RSPSA.196..343P. doi : 10.1098/rspa.1949.0032 .
^ Hume-rothery, W.; Irving, HM; Williams, RJP (1951). "Las valencias de los elementos de transición en el estado metálico". Actas de la Royal Society A . 208 (1095): 431. Bibcode :1951RSPSA.208..431H. doi :10.1098/rspa.1951.0172. S2CID 95981632.
^ Altmann, SL; Coulson, CA; Hume-Rothery, W. (1957). "Sobre la relación entre los híbridos de enlace y las estructuras metálicas". Actas de la Royal Society A . 240 (1221): 145. Bibcode :1957RSPSA.240..145A. doi :10.1098/rspa.1957.0073. S2CID 94113118.
^ Liu, Gang (2015). "Ecuaciones dinámicas para los vectores de período en un sistema periódico bajo estrés externo constante". Can. J. Phys. 93 (9): 974–978. arXiv : cond-mat/0209372 . Código Bibliográfico :2015CaJPh..93..974L. doi :10.1139/cjp-2014-0518. S2CID 54966950.
^ Hanaor, Dorian AH; Sorrell, Charles C. (2011). "Revisión de la transformación de la fase de anatasa a rutilo". Journal of Materials Science . 46 (4): 855–874. Bibcode :2011JMatS..46..855H. doi : 10.1007/s10853-010-5113-0 .
^ Molodets, AM; Nabatov, SS (2000). "Potenciales termodinámicos, diagrama de estado y transiciones de fase del estaño en compresión de choque". Alta temperatura . 38 (5): 715–721. Código Bibliográfico :2000HTemp..38..715M. doi :10.1007/BF02755923. S2CID 120417927.
^ Holleman, Arnold F.; Wiberg, Egon; Wiberg, Nils (1985). "Estaño". Lehrbuch der Anorganischen Chemie (en alemán) (91-100 ed.). Walter de Gruyter. págs. 793–800. ISBN 978-3-11-007511-3.
^ Schwartz, Mel (2002). "Estaño y aleaciones, propiedades". Enciclopedia de materiales, piezas y acabados (2.ª ed.). CRC Press. ISBN 978-1-56676-661-6.

Enlaces externos

Medios relacionados con Estructuras cristalinas en Wikimedia Commons

La estructura interna de los cristales... Cristalografía para principiantes
Diferentes tipos de estructura cristalina
Apéndice A del manual de Atoms, software para XAFS
Introducción a los minerales: clases y sistemas de cristales
Introducción a la cristalografía y a los sistemas minerales cristalinos
Planos de cristal e índices de Miller
Modelos de cristal 3D interactivos
Modelos específicos de Crystal 3D
Base de datos abierta de cristalografía (con más de 140.000 estructuras cristalinas)

[Solid_State_Physics_2010-1] Hook, JR; Hall, HE (2010). Física del estado sólido . Manchester Physics Series (2.ª ed.). John Wiley & Sons. ISBN 9780471928041.

[2] West, Anthony R. (1999). Química básica del estado sólido (2.ª ed.). Wiley. pág. 1. ISBN 978-0-471-98756-7.

[Space-group_symmetry-3] Tablas internacionales de cristalografía (2006). Volumen A, Simetría de grupos espaciales.

[Physics_1991-4] Enciclopedia abc de física (segunda edición), RG Lerner , GL Trigg, editores VHC, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3

[5] "4. Redes directas y recíprocas". CSIC Departamento de Cristalografía y Biología Estructural . 6 de abril de 2017 . Consultado el 18 de mayo de 2017 .

[6] Edington, JW (1975). Difracción de electrones en el microscopio electrónico . doi :10.1007/978-1-349-02595-4. ISBN 978-0-333-18292-5.

[7] Ashcroft, N .; Mermin, D. (1976). "Capítulo 7". Física del estado sólido . Brooks/Cole (Thomson Learning, Inc.). ISBN 978-0030493461.

[Sands-8] Donald E. Sands (1994). "§4-2 Ejes de tornillo y §4-3 Planos de deslizamiento". Introducción a la cristalografía (reimpresión de WA Benjamin corregida, edición de 1975). Courier-Dover. págs. 70–71. ISBN 978-0486678399.

[Physics_1994-9] Parker, CB, ed. (1994). Enciclopedia de Física McGraw Hill (2.ª ed.). McGraw-Hill. ISBN 978-0070514003.

[Ellis-10] Ellis, Arthur B.; et al. (1995). Teaching General Chemistry: A Materials Science Companion (Enseñanza de la química general: un manual de ciencia de los materiales) (3.ª ed.). Washington, DC: American Chemical Society. ISBN 084122725X.

[11] Kallay, Nikola (2000). Dinámica interfacial. CRC Press. ISBN 978-0824700065.

[12] Hogan, CM (1969). "Densidad de estados de una aleación ferromagnética aislante". Physical Review . 188 (2): 870–874. Código Bibliográfico :1969PhRv..188..870H. doi :10.1103/PhysRev.188.870.

[13] Zhang, XY; Suhl, H (1985). "Duplicaciones de períodos relacionados con ondas de espín y caos bajo bombeo transversal". Physical Review A . 32 (4): 2530–2533. Bibcode :1985PhRvA..32.2530Z. doi :10.1103/PhysRevA.32.2530. PMID 9896377.

[14] Courtney, Thomas (2000). Comportamiento mecánico de los materiales . Long Grove, IL: Waveland Press. pág. 85. ISBN 978-1-57766-425-3.

[Paulingsrules-15] L. Pauling (1929). "Los principios que determinan la estructura de los cristales iónicos complejos". J. Am. Chem. Soc. 51 (4): 1010–1026. doi :10.1021/ja01379a006.

[16] Pauling, Linus (1938). "La naturaleza de las fuerzas interatómicas en los metales". Physical Review . 54 (11): 899–904. Código Bibliográfico :1938PhRv...54..899P. doi :10.1103/PhysRev.54.899.

[17] Pauling, Linus (1947). "Radios atómicos y distancias interatómicas en metales". Revista de la Sociedad Química Americana . 69 (3): 542–553. doi :10.1021/ja01195a024.

[18] Pauling, L. (1949). "Una teoría de enlace de valencia resonante de metales y compuestos intermetálicos". Actas de la Royal Society A . 196 (1046): 343–362. Bibcode :1949RSPSA.196..343P. doi : 10.1098/rspa.1949.0032 .

[19] Hume-rothery, W.; Irving, HM; Williams, RJP (1951). "Las valencias de los elementos de transición en el estado metálico". Actas de la Royal Society A . 208 (1095): 431. Bibcode :1951RSPSA.208..431H. doi :10.1098/rspa.1951.0172. S2CID 95981632.

[20] Altmann, SL; Coulson, CA; Hume-Rothery, W. (1957). "Sobre la relación entre los híbridos de enlace y las estructuras metálicas". Actas de la Royal Society A . 240 (1221): 145. Bibcode :1957RSPSA.240..145A. doi :10.1098/rspa.1957.0073. S2CID 94113118.

[21] Liu, Gang (2015). "Ecuaciones dinámicas para los vectores de período en un sistema periódico bajo estrés externo constante". Can. J. Phys. 93 (9): 974–978. arXiv : cond-mat/0209372 . Código Bibliográfico :2015CaJPh..93..974L. doi :10.1139/cjp-2014-0518. S2CID 54966950.

[22] Hanaor, Dorian AH; Sorrell, Charles C. (2011). "Revisión de la transformación de la fase de anatasa a rutilo". Journal of Materials Science . 46 (4): 855–874. Bibcode :2011JMatS..46..855H. doi : 10.1007/s10853-010-5113-0 .

[23] Molodets, AM; Nabatov, SS (2000). "Potenciales termodinámicos, diagrama de estado y transiciones de fase del estaño en compresión de choque". Alta temperatura . 38 (5): 715–721. Código Bibliográfico :2000HTemp..38..715M. doi :10.1007/BF02755923. S2CID 120417927.

[24] Holleman, Arnold F.; Wiberg, Egon; Wiberg, Nils (1985). "Estaño". Lehrbuch der Anorganischen Chemie (en alemán) (91-100 ed.). Walter de Gruyter. págs. 793–800. ISBN 978-3-11-007511-3.

[25] Schwartz, Mel (2002). "Estaño y aleaciones, propiedades". Enciclopedia de materiales, piezas y acabados (2.ª ed.). CRC Press. ISBN 978-1-56676-661-6.