Edad del universo
Tiempo transcurrido desde el Big Bang

Parte de una serie sobre
Cosmología física
Imagen de cielo completo derivada de nueve años de datos WMAP
Universo primitivo
Antecedentes
Expansión  · Futuro
Componentes  · Estructura
Componentes
Estructura
Experimentos
Científicos
Historial del tema

En cosmología física , la edad del universo es el tiempo transcurrido desde el Big Bang . Los astrónomos han derivado dos medidas diferentes de la edad del universo : [1] una medida basada en observaciones directas de un estado temprano del universo, que indica una edad de13.787 ± 0,020  mil millones de años según la interpretación del modelo de concordancia Lambda-CDM a partir de 2021; [2] y una medición basada en las observaciones del universo local moderno, que sugieren una edad más joven. [3] [4] [5] La incertidumbre del primer tipo de medición se ha reducido a 20 millones de años, basándose en una serie de estudios que muestran cifras similares para la edad. Estos estudios incluyen investigaciones de la radiación de fondo de microondas realizadas por la nave espacial Planck , la sonda de anisotropía de microondas Wilkinson y otras sondas espaciales. Las mediciones de la radiación de fondo cósmico dan el tiempo de enfriamiento del universo desde el Big Bang, [6] y las mediciones de la tasa de expansión del universo se pueden utilizar para calcular su edad aproximada extrapolando hacia atrás en el tiempo. El rango de la estimación también está dentro del rango de la estimación de la estrella más antigua observada en el universo.

Historia

En el siglo XVIII empezó a aparecer el concepto de que la edad de la Tierra era de millones, si no miles de millones, de años. No obstante, la mayoría de los científicos a lo largo del siglo XIX y las primeras décadas del siglo XX supusieron que el universo en sí era estable y eterno, posiblemente con estrellas que iban y venían pero sin que se produjeran cambios en la mayor escala conocida en ese momento. [7]

Las primeras teorías científicas que indicaban que la edad del universo podría ser finita fueron los estudios de la termodinámica , formalizados a mediados del siglo XIX. El concepto de entropía dicta que si el universo (o cualquier otro sistema cerrado) fuera infinitamente viejo, entonces todo lo que hay en su interior estaría a la misma temperatura y, por lo tanto, no habría estrellas ni vida. En aquel momento no se propuso ninguna explicación científica para esta contradicción.

En 1915, Albert Einstein publicó la teoría de la relatividad general [8] y en 1917 construyó el primer modelo cosmológico basado en su teoría. Para mantener la coherencia con un universo en estado estacionario, Einstein añadió a sus ecuaciones lo que más tarde se denominó una constante cosmológica . El modelo de Einstein de un universo estático fue demostrado como inestable por Arthur Eddington .

El primer indicio observacional directo de que el universo no era estático sino que se expandía provino de las observaciones de " velocidades de recesión ", principalmente por Vesto M. Slipher , combinadas con distancias a las " nebulosas " ( galaxias ) por Edwin Hubble en un trabajo publicado en 1929. [9] A principios del siglo XX, Hubble y otros resolvieron estrellas individuales dentro de ciertas nebulosas, determinando así que eran galaxias, similares a, pero externas a, la Vía Láctea . Además, estas galaxias eran muy grandes y muy lejanas. Los espectros tomados de estas galaxias distantes mostraron un corrimiento al rojo en sus líneas espectrales presumiblemente causado por el efecto Doppler , lo que indica que estas galaxias se estaban alejando de la Tierra. Además, cuanto más lejos parecían estar estas galaxias (más tenues parecían) mayor era su corrimiento al rojo y, por lo tanto, más rápido parecían alejarse. Esta fue la primera evidencia directa de que el universo no es estático sino que se expande. La primera estimación de la edad del universo se basó en el cálculo de cuándo todos los objetos debieron haber comenzado a alejarse a toda velocidad del mismo punto. El valor inicial de Hubble para la edad del universo era muy bajo, ya que se suponía que las galaxias estaban mucho más cerca de lo que las observaciones posteriores demostraron.

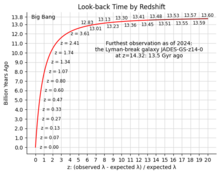
El tiempo de retrospección de las observaciones extragalácticas por su corrimiento al rojo hasta z=20 [10]

La primera medición razonablemente precisa de la tasa de expansión del universo, un valor numérico ahora conocido como la constante de Hubble , fue realizada en 1958 por el astrónomo Allan Sandage . [11] Su valor medido para la constante de Hubble estuvo muy cerca del rango de valores generalmente aceptado hoy.

Sandage, al igual que Einstein, no creía en sus propios resultados en el momento del descubrimiento. [ cita requerida ] Sandage propuso nuevas teorías de cosmogonía para explicar esta discrepancia. Este problema se resolvió más o menos mediante mejoras en los modelos teóricos utilizados para estimar las edades de las estrellas. A partir de 2024, utilizando los últimos modelos de evolución estelar, la edad estimada de la estrella más antigua conocida es13,8 ± 4 mil millones de años. [12]

El descubrimiento de la radiación de fondo cósmico de microondas , anunciado en 1965 [13], finalmente puso fin de manera efectiva a la incertidumbre científica restante sobre el universo en expansión. Fue un resultado casual del trabajo de dos equipos a menos de 60 millas de distancia. En 1964, Arno Penzias y Robert Woodrow Wilson estaban tratando de detectar ecos de ondas de radio con una antena supersensible. La antena detectó persistentemente un ruido bajo, constante y misterioso en la región de microondas que se extendía uniformemente por el cielo y estaba presente día y noche. Después de las pruebas, se aseguraron de que la señal no provenía de la Tierra , el Sol o la Vía Láctea , sino de fuera de la Vía Láctea, pero no pudieron explicarlo. Al mismo tiempo, otro equipo, Robert H. Dicke , Jim Peebles y David Wilkinson , estaban tratando de detectar ruido de bajo nivel que podría ser un remanente del Big Bang y podrían probar si la teoría del Big Bang era correcta. Los dos equipos se dieron cuenta de que el ruido detectado era de hecho radiación remanente del Big Bang, y que esto era una fuerte evidencia de que la teoría era correcta. Desde entonces, una gran cantidad de otras evidencias han fortalecido y confirmado esta conclusión y han refinado la edad estimada del universo hasta su cifra actual.

Las sondas espaciales WMAP, lanzada en 2001, y Planck , lanzada en 2009, produjeron datos que determinan la constante de Hubble y la edad del universo independientemente de las distancias entre galaxias, eliminando la mayor fuente de error. [14]

Explicación

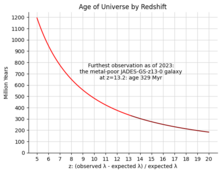
Relación entre el corrimiento al rojo y la edad del universo, desde z=5 hasta 20 [10]

El modelo de concordancia Lambda-CDM describe la evolución del universo desde un estado primordial muy uniforme, caliente y denso hasta su estado actual a lo largo de un lapso de aproximadamente 13.77 mil millones de años [15] de tiempo cosmológico . Este modelo se entiende bien teóricamente y está fuertemente respaldado por recientes observaciones astronómicas de alta precisión como WMAP . En contraste, las teorías sobre el origen del estado primordial siguen siendo muy especulativas.

Si extrapolamos el modelo Lambda-CDM hacia atrás desde el estado más antiguo bien comprendido, rápidamente (en una pequeña fracción de segundo) se alcanza una singularidad . Esto se conoce como la " singularidad inicial " o la " singularidad del Big Bang ". Esta singularidad no se entiende como algo que tenga un significado físico en el sentido habitual, pero es conveniente citar tiempos medidos "desde el Big Bang" aunque no correspondan a un tiempo que realmente pueda medirse físicamente.

Aunque en teoría el universo podría tener una historia más larga, la Unión Astronómica Internacional actualmente utiliza el término "edad del universo" para referirse a la duración de la expansión Lambda-CDM [16] o, equivalentemente, el tiempo transcurrido dentro del universo actualmente observable desde el Big Bang.

En julio de 2023, un estudio publicado en la revista Monthly Notices of the Royal Astronomical Society situó la edad del Universo en 26.700 millones de años. [17] [18] El autor Rajendra Gupta muestra un nuevo modelo que alarga el tiempo de formación de las galaxias varios miles de millones de años, lo que lleva a la conclusión de que la edad del Universo es aproximadamente el doble de lo que se pensaba. [17] [18] Utilizando la teoría de la luz cansada de Zwicky y las "constantes de acoplamiento" descritas por Paul Dirac , Gupta escribe que las recientes observaciones del Telescopio Espacial James Webb están en fuerte tensión con los modelos cosmológicos existentes. [17] Gupta dice sobre su nueva teoría: "Resuelve así el problema de la 'galaxia primitiva imposible' sin requerir la existencia de semillas de agujeros negros primordiales o espectro de potencia modificado". [17]

Límites de observación

Dado que el universo debe ser al menos tan antiguo como las cosas más antiguas que contiene, hay una serie de observaciones que establecen un límite inferior para la edad del universo; [19] [20] estas incluyen

  • la temperatura de las enanas blancas más frías , que se enfrían gradualmente a medida que envejecen, y
  • el punto de inflexión más tenue de las estrellas de la secuencia principal en los cúmulos (las estrellas de menor masa pasan una mayor cantidad de tiempo en la secuencia principal, por lo que las estrellas de menor masa que han evolucionado lejos de la secuencia principal establecen una edad mínima).

Parámetros cosmológicos

La edad del universo se puede determinar midiendo la constante de Hubble hoy y extrapolando hacia atrás en el tiempo con el valor observado de los parámetros de densidad ( ). Antes del descubrimiento de la energía oscura , se creía que el universo estaba dominado por la materia ( universo de Einstein-de Sitter , curva verde). El universo de De Sitter tiene una edad infinita, mientras que el universo cerrado tiene la edad más baja.   Ω   {\displaystyle ~\Omega ~}
El valor del factor de corrección de edad se muestra como una función de dos parámetros cosmológicos : la densidad de materia fraccionaria actual y la densidad constante cosmológica. Los valores de mejor ajuste de estos parámetros se muestran mediante el cuadro en la parte superior izquierda; el universo dominado por la materia se muestra mediante la estrella en la parte inferior derecha.   F   , {\displaystyle ~F~,}   Ω m   {\displaystyle ~\Omega _{\text{m}}~}   Ω Λ   . {\displaystyle ~\Omega _{\Lambda }~.}

El problema de determinar la edad del universo está estrechamente ligado al problema de determinar los valores de los parámetros cosmológicos. Hoy en día, esto se lleva a cabo en gran medida en el contexto del modelo ΛCDM , en el que se supone que el universo contiene materia normal (bariónica), materia oscura fría , radiación (que incluye tanto fotones como neutrinos ) y una constante cosmológica .

La contribución fraccionaria de cada uno a la densidad de energía actual del universo está dada por los parámetros de densidad y El modelo ΛCDM completo se describe mediante una serie de otros parámetros, pero para el propósito de calcular su edad estos tres, junto con el parámetro de Hubble , son los más importantes.   Ω m   , {\displaystyle ~\Omega _{\text{m}}~,}   Ω r   , {\displaystyle ~\Omega _{\text{r}}~,}   Ω Λ   . {\displaystyle ~\Omega _{\Lambda }~.}   H 0   {\displaystyle ~H_{0}~}

Si se tienen medidas precisas de estos parámetros, se puede determinar la edad del universo utilizando la ecuación de Friedmann . Esta ecuación relaciona la tasa de cambio en el factor de escala con el contenido de materia del universo. Dando la vuelta a esta relación, podemos calcular el cambio en el tiempo por cambio en el factor de escala y, por lo tanto, calcular la edad total del universo integrando esta fórmula. La edad se da entonces mediante una expresión de la forma   a ( t )   {\displaystyle ~a(t)~}   t 0   {\displaystyle ~t_{0}~}

t 0 = 1 H 0 F ( Ω r , Ω m , Ω Λ , … )   {\displaystyle t_{0}={\frac {1}{H_{0}}}\,F(\,\Omega _{\text{r}},\,\Omega _{\text{m}},\,\Omega _{\Lambda },\,\dots \,)~}

donde es el parámetro de Hubble y la función depende únicamente de la contribución fraccionaria al contenido de energía del universo que proviene de varios componentes. La primera observación que se puede hacer a partir de esta fórmula es que es el parámetro de Hubble el que controla la edad del universo, con una corrección que surge del contenido de materia y energía. Por lo tanto, una estimación aproximada de la edad del universo proviene del tiempo de Hubble , el inverso del parámetro de Hubble. Con un valor de alrededor de   H 0   {\displaystyle ~H_{0}~}   F   {\displaystyle ~F~}   H 0   {\displaystyle ~H_{0}~} 69 km/s/Mpc , el tiempo de Hubble se evalúa como   1 / H 0 =   {\displaystyle ~1/H_{0}=~} 14.500  millones de años. [21]

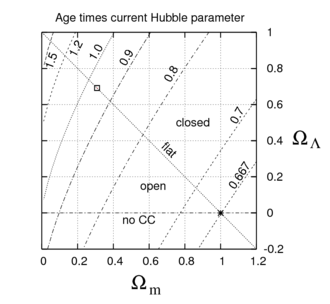
Para obtener un número más preciso, se debe calcular la función de corrección . En general, esto se debe hacer numéricamente, y los resultados para un rango de valores de parámetros cosmológicos se muestran en la figura. Para los valores de Planck (0,3086, 0,6914), mostrados por el recuadro en la esquina superior izquierda de la figura, este factor de corrección es de aproximadamente Para un universo plano sin ninguna constante cosmológica, mostrado por la estrella en la esquina inferior derecha, es mucho menor y, por lo tanto, el universo es más joven para un valor fijo del parámetro de Hubble. Para hacer esta figura, se mantiene constante (aproximadamente equivalente a mantener constante la temperatura del fondo cósmico de microondas ) y el parámetro de densidad de curvatura se fija por el valor de los otros tres.   F   {\displaystyle ~F~}   ( Ω m , Ω Λ ) =   {\displaystyle ~(\Omega _{\text{m}},\Omega _{\Lambda })=~}   F = 0.956   . {\displaystyle ~F=0.956~.}   F = 2 / 3   {\displaystyle ~F={2}/{3}~}   Ω r   {\displaystyle ~\Omega _{\text{r}}~}

Aparte del satélite Planck, la sonda de anisotropía de microondas Wilkinson ( WMAP ) fue fundamental para establecer una edad precisa del universo, aunque se deben incluir otras mediciones para obtener un número preciso. Las mediciones del CMB son muy buenas para restringir el contenido de materia [22] y el parámetro de curvatura [23] No es tan sensible a directamente, [23] en parte porque la constante cosmológica se vuelve importante solo en corrimientos al rojo bajos. Actualmente se cree que las determinaciones más precisas del parámetro de Hubble provienen de brillos medidos y corrimientos al rojo de supernovas distantes de tipo Ia . La combinación de estas mediciones conduce al valor generalmente aceptado para la edad del universo citado anteriormente.   Ω m   , {\displaystyle ~\Omega _{\text{m}}~,}   Ω k   . {\displaystyle ~\Omega _{\text{k}}~.}   Ω Λ   {\displaystyle ~\Omega _{\Lambda }~}   H 0   {\displaystyle ~H_{0}~}

La constante cosmológica hace que el universo sea "más viejo" para valores fijos de los otros parámetros. Esto es significativo, ya que antes de que la constante cosmológica fuera aceptada de manera general, el modelo del Big Bang tenía dificultades para explicar por qué los cúmulos globulares de la Vía Láctea parecían ser mucho más viejos que la edad del universo calculada a partir del parámetro de Hubble y un universo compuesto únicamente de materia. [24] [25] La introducción de la constante cosmológica permite que el universo sea más viejo que estos cúmulos, además de explicar otras características que el modelo cosmológico basado únicamente en materia no podía explicar. [26]

Mapa del mundo

La publicación de datos de nueve años del proyecto Wilkinson Microwave Anisotropy Probe (WMAP) de la NASA en 2012 estimó que la edad del universo era(13,772 ± 0,059) × 10 9 años (13,772 mil millones de años, con una incertidumbre de más o menos 59 millones de años). [6]

Esta edad se basa en el supuesto de que el modelo subyacente del proyecto es correcto; otros métodos de estimación de la edad del universo podrían dar edades diferentes. Suponiendo un fondo adicional de partículas relativistas, por ejemplo, se pueden ampliar las barras de error de la restricción WMAP en un orden de magnitud. [27]

Esta medición se realiza utilizando la ubicación del primer pico acústico en el espectro de potencia del fondo de microondas para determinar el tamaño de la superficie de desacoplamiento (tamaño del universo en el momento de la recombinación). El tiempo de viaje de la luz hasta esta superficie (dependiendo de la geometría utilizada) proporciona una edad fiable para el universo. Suponiendo la validez de los modelos utilizados para determinar esta edad, la precisión residual arroja un margen de error cercano al uno por ciento. [14]

Planck

En 2015, la Colaboración Planck estimó la edad del universo en13.813 ± 0.038  mil millones de años, ligeramente más alto pero dentro de las incertidumbres del número anterior derivado de los datos WMAP. [28]

En la siguiente tabla, las cifras están dentro de los límites de confianza del 68% para el modelo base ΛCDM .

Parámetros cosmológicos de los resultados de Planck de 2015 [28]
ParámetroSímboloTT + baja presiónTT + lowP + efecto lenteTT + lowP + lente + extTT, TE, EE + baja presiónTT, TE, EE + lowP + efecto lenteTT, TE, EE + lowP + efecto lente + ext
Edad del universo
(Ga)		 t 0 {\displaystyle t_{0}} 13,813 ± 0,03813,799 ± 0,03813,796 ± 0,02913,813 ± 0,02613,807 ± 0,02613,799 ± 0,021
Constante de Hubble
( km / Mpc⋅s )		 H 0 {\displaystyle H_{0}} 67,31 ± 0,9667,81 ± 0,9267,90 ± 0,5567,27 ± 0,6667,51 ± 0,6467,74 ± 0,46

Leyenda:

En 2018, la Colaboración Planck actualizó su estimación de la edad del universo a13.787 ± 0.020  mil millones de años. [2]

Suposición de fuertes principios

El cálculo de la edad del universo es preciso sólo si las suposiciones incorporadas en los modelos que se utilizan para estimarla también son precisas. Esto se conoce como hipótesis previas sólidas y básicamente implica eliminar los posibles errores en otras partes del modelo para convertir la precisión de los datos de observación reales directamente en el resultado final. La edad dada es, por tanto, precisa hasta el error especificado, ya que este representa el error en el instrumento utilizado para recopilar los datos brutos que se introducen en el modelo.

La edad del universo basada únicamente en el mejor ajuste a los datos de Planck 2018 es13.787 ± 0,020 mil millones de años. Este número representa una medición "directa" precisa de la edad del universo, en contraste con otros métodos que generalmente involucran la ley de Hubble y la edad de las estrellas más antiguas en los cúmulos globulares . Es posible utilizar diferentes métodos para determinar el mismo parámetro (en este caso, la edad del universo) y llegar a diferentes respuestas sin superposición en los "errores". Para evitar mejor el problema, es común mostrar dos conjuntos de incertidumbres: uno relacionado con la medición real y el otro relacionado con los errores sistemáticos del modelo que se está utilizando.

Por lo tanto , un componente importante del análisis de los datos utilizados para determinar la edad del universo (por ejemplo, de Planck ) es utilizar un análisis estadístico bayesiano , que normaliza los resultados en función de los datos anteriores (es decir, el modelo). [14] Esto cuantifica cualquier incertidumbre en la precisión de una medición debido a un modelo particular utilizado. [29] [30]

Véase también

Referencias

  1. ^ "De un Universo casi perfecto a lo mejor de ambos mundos". Misión Planck. sci.esa.int . Agencia Espacial Europea . 17 de julio de 2018. Últimos párrafos. Archivado desde el original el 13 de abril de 2020.
  2. ^ ab Planck Collaboration (2020). "Resultados del Planck 2018. VI. Parámetros cosmológicos". Astronomy & Astrophysics . 641 . página A6 (ver PDF página 15, Tabla 2: "Edad/Gyr", última columna). arXiv : 1807.06209 . Bibcode :2020A&A...641A...6P. doi : 10.1051/0004-6361/201833910 . S2CID  119335614.
  3. ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; Bucciarelli, Beatrice; Lattanzi, Mario G.; et al. (12 de julio de 2018). "Estándares de cefeidas de la Vía Láctea para medir distancias cósmicas y aplicación a Gaia DR2: implicaciones para la constante de Hubble". The Astrophysical Journal . 861 (2): 126. arXiv : 1804.10655 . Bibcode :2018ApJ...861..126R. doi : 10.3847/1538-4357/aac82e . ISSN  1538-4357. S2CID  55643027.
  4. ^ ESA/Planck Collaboration (17 de julio de 2018). «Medidas de la constante de Hubble». sci.esa.int . Agencia Espacial Europea . Archivado desde el original el 6 de octubre de 2020.
  5. ^ Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (29 de agosto de 2019). "El programa Hubble de Carnegie-Chicago. VIII. Una determinación independiente de la constante de Hubble basada en la punta de la rama gigante roja". The Astrophysical Journal . 882 (1): 34. arXiv : 1907.05922 . Bibcode :2019ApJ...882...34F. doi : 10.3847/1538-4357/ab2f73 . ISSN  1538-4357. S2CID  196623652.
  6. ^ ab Bennett, CL; et al. (2013). "Observaciones de nueve años de la sonda de anisotropía de microondas Wilkinson (WMAP): mapas finales y resultados". The Astrophysical Journal Supplement Series . 208 (2): 20. arXiv : 1212.5225 . Bibcode :2013ApJS..208...20B. doi :10.1088/0067-0049/208/2/20. S2CID  119271232.
  7. ^ Heilborn, JL, ed. (2005). Guía Oxford de la historia de la física y la astronomía. Oxford University Press. pág. 312. ISBN 978-0-19-517198-3.
  8. ^ Einstein, A. (1915). "Zur allgemeinen Relativitätstheorie" [Sobre la teoría general de la relatividad]. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (en alemán): 778–786. Código bibliográfico : 1915SPAW.......778E.
  9. ^ Hubble, E. (1929). "Una relación entre la distancia y la velocidad radial entre nebulosas extragalácticas". Actas de la Academia Nacional de Ciencias . 15 (3): 168–173. Bibcode :1929PNAS...15..168H. doi : 10.1073/pnas.15.3.168 . PMC 522427 . PMID  16577160. 
  10. ^ ab Pilipenko, Sergey V. (2013). "Calculadora cosmológica de papel y lápiz". arXiv : 1303.5961 [astro-ph.CO].Código Fortran-90 en el que se basan los cuadros y fórmulas de citación.
  11. ^ Sandage, AR (1958). "Problemas actuales en la escala de distancias extragalácticas". The Astrophysical Journal . 127 (3): 513–526. Bibcode :1958ApJ...127..513S. doi :10.1086/146483.
  12. ^ Cowan, John J.; Sneden, Christopher; Burles, Scott; Ivans, Inese I.; Cervezas, Timothy C.; Truran, James W.; et al. (junio de 2002). "La composición química y la edad de la estrella Halo pobre en metales BD +17 ° 3248". La revista astrofísica . 572 (2): 861–879. arXiv : astro-ph/0202429 . Código bibliográfico : 2002ApJ...572..861C. doi :10.1086/340347. S2CID  119503888.
  13. ^ Penzias, AA; Wilson, R .W. (1965). "Una medición del exceso de temperatura de la antena a 4080 Mc/s". The Astrophysical Journal . 142 : 419–421. Bibcode :1965ApJ...142..419P. doi : 10.1086/148307 .
  14. ^ abc Spergel, DN; et al. (2003). "Observaciones del primer año de la sonda de anisotropía de microondas Wilkinson (WMAP): determinación de parámetros cosmológicos". The Astrophysical Journal Supplement Series . 148 (1): 175–194. arXiv : astro-ph/0302209 . Código Bibliográfico :2003ApJS..148..175S. doi :10.1086/377226. S2CID  10794058.
  15. ^ "Detectives cósmicos". Agencia Espacial Europea . 2 de abril de 2013. Consultado el 15 de abril de 2013 .
  16. ^ Chang, K. (9 de marzo de 2008). "La medición de la edad del universo se vuelve más precisa". The New York Times .
  17. ^ abcd Rajendra P. Gupta (7 de julio de 2023). «Observaciones del universo temprano del JWST y cosmología ΛCDM». Monthly Notices of the Royal Astronomical Society . 524 (3): 3385–3395. arXiv : 2309.13100 . doi : 10.1093/mnras/stad2032 . Consultado el 22 de enero de 2024 .
  18. ^ ab Rizk, B. (13 de julio de 2023). «Una nueva investigación sitúa la edad del universo en 26.700 millones de años, casi el doble de lo que se creía anteriormente». Phys.org . Consultado el 22 de enero de 2024 .
  19. ^ Chaboyer, Brian (1 de diciembre de 1998). "La edad del universo". Physics Reports . 307 (1–4): 23–30. arXiv : astro-ph/9808200 . Bibcode :1998PhR...307...23C. doi :10.1016/S0370-1573(98)00054-4. S2CID  119491951.
  20. ^ Chaboyer, Brian (16 de febrero de 1996). "Un límite inferior para la edad del universo". Science . 271 (5251): 957–961. arXiv : astro-ph/9509115 . Bibcode :1996Sci...271..957C. doi :10.1126/science.271.5251.957. S2CID  952053.
  21. ^ Liddle, AR (2003). Introducción a la cosmología moderna (2.ª ed.). Wiley . p. 57. ISBN 978-0-470-84835-7.
  22. ^ Hu, W. "Animación: Sensibilidad del contenido de materia. La relación materia-radiación se eleva mientras se mantienen fijos todos los demás parámetros". Universidad de Chicago . Archivado desde el original el 23 de febrero de 2008. Consultado el 23 de febrero de 2008 .
  23. ^ ab Hu, W. "Animación: Escalado de distancia de diámetro angular con curvatura y lambda". Universidad de Chicago . Archivado desde el original el 23 de febrero de 2008. Consultado el 23 de febrero de 2008 .
  24. ^ "Cúmulos globulares de estrellas". SEDS . 1 de julio de 2011. Archivado desde el original el 24 de febrero de 2008 . Consultado el 19 de julio de 2013 .
  25. ^ Iskander, E. (11 de enero de 2006). «Independent age estimate». Universidad de Columbia Británica . Archivado desde el original el 6 de marzo de 2008. Consultado el 23 de febrero de 2008 .
  26. ^ Ostriker, JP; Steinhardt, PJ (1995). "Concordancia cósmica". arXiv : astro-ph/9505066 .
  27. ^ de Bernardis, F.; Melchiorri, A.; Verde, L.; Jiménez, R. (2008). "El fondo cósmico de neutrinos y la edad del universo". Revista de Cosmología y Física de Astropartículas . 2008 (3): 20. arXiv : 0707.4170 . Bibcode :2008JCAP...03..020D. doi :10.1088/1475-7516/2008/03/020. S2CID  8896110.
  28. ^ ab Planck Collaboration (2016). "Planck 2015 results. XIII. Cosmological parameters". Astronomy & Astrophysics . 594 . página A13 (ver PDF página 32, Tabla 4: "Age/Gyr", última columna). arXiv : 1502.01589 . Bibcode :2016A&A...594A..13P. doi :10.1051/0004-6361/201525830. S2CID  119262962.
  29. ^ Loredo, TJ (1992). "La promesa de la inferencia bayesiana para la astrofísica" (PDF) . En Feigelson, ED; Babu, GJ (eds.). Desafíos estadísticos en la astronomía moderna . Springer-Verlag . pp. 275–297. Bibcode :1992scma.conf..275L. doi :10.1007/978-1-4613-9290-3_31. ISBN . 978-1-4613-9292-7.
  30. ^ Colistete, R.; Fabris, JC; Concalves, SVB (2005). "Estadísticas bayesianas y restricciones de parámetros en el modelo generalizado de gas de Chaplygin utilizando datos de SNe ia". Revista Internacional de Física Moderna D . 14 (5): 775–796. arXiv : astro-ph/0409245 . Código Bibliográfico :2005IJMPD..14..775C. doi :10.1142/S0218271805006729. S2CID  14184379.
  • Wright, Ned. "Tutorial de cosmología". División de Astronomía y Astrofísica (sitio personal académico). Universidad de California, Los Ángeles .
  • Wright, Edward L. (2 de julio de 2005). "La edad del universo". División de Astronomía y Astrofísica (sitio personal académico). Universidad de California, Los Ángeles .
  • Hu, Wayne. "Animaciones de parámetros cosmológicos" (sitio personal académico). Universidad de Chicago .
  • Ostriker, JP; Steinhardt, PJ (1995). "Concordancia cósmica". arXiv : astro-ph/9505066 .
  • "Cúmulos globulares de estrellas". SEDS . Archivado desde el original el 30 de abril de 2015.
  • Scott, Douglas. "Estimaciones de edad independientes" (sitio personal académico). Vancouver, BC: Universidad de Columbia Británica .
  • "La escala del universo". KryssTal .— Espacio y tiempo a escala para principiantes.
  • "Calculadora de cosmología (con generación de gráficos)". iCosmos .
  • "El universo en expansión". Instituto Americano de Física .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Age_of_the_universe&oldid=1250049443"