Dispersión de luz estática
La dispersión de luz estática es una técnica de la química física que mide la intensidad de la luz dispersada para obtener el peso molecular promedio M w de una macromolécula como un polímero o una proteína en solución. La medición de la intensidad de dispersión en muchos ángulos permite calcular el radio cuadrático medio, también llamado radio de giro R g . Al medir la intensidad de dispersión para muchas muestras de varias concentraciones, se puede calcular el segundo coeficiente virial, A 2 . [1] [2] [3] [4] [5]
La dispersión de luz estática también se utiliza comúnmente para determinar el tamaño de suspensiones de partículas en los rangos sub-μm y supra-μm, a través de los formalismos de difracción de Lorenz-Mie (ver dispersión de Mie ) y de Fraunhofer , respectivamente.
Para los experimentos de dispersión de luz estática, se lanza una luz monocromática de alta intensidad, normalmente un láser, en una solución que contiene las macromoléculas. Se utilizan uno o varios detectores para medir la intensidad de dispersión en uno o varios ángulos. La dependencia angular es necesaria para obtener mediciones precisas tanto de la masa molar como del tamaño de todas las macromoléculas con un radio superior al 1-2% de la longitud de onda incidente. Por lo tanto, las mediciones simultáneas en varios ángulos en relación con la dirección de la luz incidente, conocidas como dispersión de luz multiángulo (MALS) o dispersión de luz láser multiángulo (MALLS), se consideran generalmente como la implementación estándar de la dispersión de luz estática. Se pueden encontrar detalles adicionales sobre la historia y la teoría de MALS en dispersión de luz multiángulo .
Para medir el peso molecular promedio directamente sin calibración a partir de la intensidad de dispersión de la luz, es necesario conocer la intensidad del láser, la eficiencia cuántica del detector y el volumen de dispersión total y el ángulo sólido del detector. Como esto no es práctico, todos los instrumentos comerciales se calibran utilizando un dispersor potente y conocido, como el tolueno, ya que la relación de Rayleigh del tolueno y algunos otros solventes se midieron utilizando un instrumento de dispersión de luz absoluta.
Teoría
En el caso de un instrumento de dispersión de luz compuesto por muchos detectores colocados en distintos ángulos, todos los detectores deben responder de la misma manera. Por lo general, los detectores tendrán una eficiencia cuántica ligeramente diferente , diferentes ganancias y están considerando diferentes volúmenes de dispersión geométrica. En este caso, es absolutamente necesaria una normalización de los detectores. Para normalizar los detectores, primero se realiza una medición de un disolvente puro. Luego, se agrega un dispersor isotrópico al disolvente. Dado que los dispersores isotrópicos dispersan la misma intensidad en cualquier ángulo, la eficiencia y la ganancia del detector se pueden normalizar con este procedimiento. Es conveniente normalizar todos los detectores al detector con un ángulo de 90°.
donde IR (90) es la intensidad de dispersión medida para el dispersor Rayleigh por el detector de ángulo de 90° .
La ecuación más común para medir el peso molecular promedio en peso, M w , es la ecuación de Zimm [5] (el lado derecho de la ecuación de Zimm se proporciona incorrectamente en algunos textos, como lo señalan Hiemenz y Lodge): [6]
dónde
y
con
y el vector de dispersión para la luz polarizada verticalmente es
con n 0 el índice de refracción del solvente, λ la longitud de onda de la fuente de luz, N A la constante de Avogadro , c la concentración de la solución, y d n /d c el cambio en el índice de refracción de la solución con el cambio en la concentración. La intensidad del analito medida en un ángulo es I A (θ) . En estas ecuaciones, el subíndice A es para el analito (la solución) y T es para el tolueno con la relación de Rayleigh del tolueno, siendo R T 1.35×10 −5 cm −1 para un láser HeNe . Como se describió anteriormente, el radio de giro, R g , y el segundo coeficiente virial, A 2 , también se calculan a partir de esta ecuación. El incremento del índice de refracción dn/dc caracteriza el cambio del índice de refracción n con la concentración c y se puede medir con un refractómetro diferencial.
Un diagrama de Zimm se construye a partir de una doble extrapolación a ángulo cero y concentración cero desde muchos ángulos y muchas mediciones de concentración. En su forma más simple, la ecuación de Zimm se reduce a:
para mediciones realizadas en ángulo bajo y dilución infinita ya que P (0) = 1.
Existen varios análisis desarrollados para analizar la dispersión de partículas en solución y obtener las características físicas de las partículas mencionadas anteriormente. Un experimento simple de dispersión de luz estática implica que la intensidad promedio de la muestra que se corrige para la dispersión del solvente dará como resultado la relación de Rayleigh, R, en función del ángulo o el vector de onda q, como se muestra a continuación:
Análisis de datos
El complot de Guinier
La intensidad dispersa se puede representar gráficamente como una función del ángulo para brindar información sobre R g, que puede calcularse simplemente utilizando la aproximación de Guinier de la siguiente manera:
donde ln(ΔR(θ)) = lnP(θ) también conocido como el factor de forma con q = 4πn 0 sen(θ/2)/λ . Por lo tanto, un gráfico de la relación de Rayleigh corregida, ΔR(θ) vs sen 2 (θ/2) o q 2 producirá una pendiente R g 2 /3 . Sin embargo, esta aproximación solo es cierta para qR g < 1 . Tenga en cuenta que para un gráfico de Guinier, el valor de dn/dc y la concentración no son necesarios.
El complot de Kratky
El diagrama de Kratky se utiliza normalmente para analizar la conformación de las proteínas , pero se puede utilizar para analizar el modelo de recorrido aleatorio de los polímeros . Se puede crear un diagrama de Kratky trazando sin 2 (θ/2)ΔR(θ) vs sin(θ/2) o q 2 ΔR(θ) vs q .
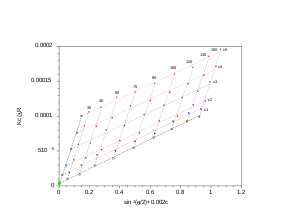
Parcela de Zimm
Para polímeros y complejos poliméricos que son monodispersos ( ) según lo determinado por dispersión de luz estática, un diagrama de Zimm es un medio convencional para derivar parámetros como R g , masa molecular M w y el segundo coeficiente virial A 2 .
Cabe señalar que si no se implementa la constante material K , un gráfico de Zimm solo dará como resultado R g . Por lo tanto, si se implementa K, se obtendrá la siguiente ecuación:
El análisis realizado con el gráfico de Zimm utiliza una extrapolación doble a concentración cero y ángulo de dispersión cero, lo que da como resultado un gráfico romboidal característico. Como la información angular está disponible, también es posible obtener el radio de giro ( R g ). Los experimentos se realizan en varios ángulos, que satisfacen la condición y al menos 4 concentraciones. La realización de un análisis de Zimm en una sola concentración se conoce como análisis de Zimm parcial y solo es válido para soluciones diluidas de dispersores puntuales fuertes. Sin embargo, el Zimm parcial no produce el segundo coeficiente virial , debido a la ausencia de la concentración variable de la muestra. Más específicamente, el valor del segundo coeficiente virial se supone igual a cero o se ingresa como un valor conocido para realizar el análisis de Zimm parcial.
El complot de Debye

Si las partículas medidas son más pequeñas que λ/20, el factor de forma P(θ) puede despreciarse ( P(θ) →1). Por lo tanto, la ecuación de Zimm se simplifica a la ecuación de Debye, de la siguiente manera:
Obsérvese que este es también el resultado de una extrapolación a un ángulo de dispersión cero. Al adquirir datos sobre la concentración y la intensidad de dispersión, se construye el diagrama de Debye representando Kc / ΔR(θ) en función de la concentración. La intersección de la línea ajustada proporciona la masa molecular, mientras que la pendiente corresponde al segundo coeficiente virial.
Como el diagrama de Debye es una simplificación de la ecuación de Zimm, se aplican las mismas limitaciones de esta última, es decir, las muestras deben presentar una naturaleza monodispersa. Para muestras polidispersas, la masa molecular resultante de una medición de dispersión de luz estática representará un valor promedio. Una ventaja del diagrama de Debye es la posibilidad de determinar el segundo coeficiente virial. Este parámetro describe la interacción entre partículas y solvente. En soluciones de macromoléculas, por ejemplo, puede asumir valores negativos (se favorecen las interacciones partícula-partícula), cero o positivos (se favorecen las interacciones partícula-solvente). [8]
Dispersión múltiple
La dispersión de luz estática presupone que cada fotón detectado se ha dispersado exactamente una sola vez. Por lo tanto, el análisis según los cálculos indicados anteriormente solo será correcto si la muestra se ha diluido lo suficiente para garantizar que los fotones no se dispersen varias veces por la muestra antes de ser detectados. La interpretación precisa se vuelve extremadamente difícil para sistemas con contribuciones no despreciables de la dispersión múltiple. En muchos instrumentos comerciales donde el análisis de la señal de dispersión se realiza automáticamente, el usuario puede no notar nunca el error. En particular, para partículas más grandes y aquellas con un alto contraste de índice de refracción, esto limita la aplicación de la dispersión de luz estática estándar a concentraciones de partículas muy bajas. Por otro lado, para las macromoléculas solubles que exhiben un contraste de índice de refracción relativamente bajo en comparación con el solvente, incluidos la mayoría de los polímeros y biomoléculas en sus respectivos solventes, la dispersión múltiple rara vez es un factor limitante incluso en concentraciones que se acercan a los límites de solubilidad.
Sin embargo, como lo demuestra Schaetzel [9], es posible suprimir la dispersión múltiple en experimentos de dispersión de luz estática mediante un enfoque de correlación cruzada. La idea general es aislar la luz dispersada individualmente y suprimir las contribuciones no deseadas de la dispersión múltiple en un experimento de dispersión de luz estática. Se han desarrollado y aplicado diferentes implementaciones de dispersión de luz por correlación cruzada. Actualmente, el esquema más utilizado es el llamado método de dispersión de luz dinámica 3D. [10] [11] El mismo método también se puede utilizar para corregir los datos de dispersión de luz dinámica para las contribuciones de dispersión múltiple. [12]
Dispersión de luz estática por gradiente de composición
Las muestras que cambian sus propiedades después de la dilución no pueden analizarse mediante dispersión de luz estática en términos del modelo simple presentado aquí como la ecuación de Zimm. Un análisis más sofisticado conocido como "dispersión de luz estática (o multiángulo) de gradiente de composición" (CG-SLS o CG-MALS) es una clase importante de métodos para investigar las interacciones proteína-proteína , las propiedades coligativas y otras interacciones macromoleculares, ya que produce, además del tamaño y el peso molecular, información sobre la afinidad y la estequiometría de los complejos moleculares formados por una o más especies macromoleculares/biomoleculares asociadas. En particular, la dispersión de luz estática de una serie de diluciones puede analizarse para cuantificar la autoasociación, la oligomerización reversible y la atracción o repulsión no específica, mientras que la dispersión de luz estática de mezclas de especies puede analizarse para cuantificar la heteroasociación. [13]
Aplicaciones
Una de las principales aplicaciones de la dispersión de luz estática para la determinación de la masa molecular es en el campo de las macromoléculas, como las proteínas y los polímeros, [14] [15] [16] ya que es posible medir la masa molecular de las proteínas sin ninguna suposición sobre su forma. La dispersión de luz estática suele combinarse con otras técnicas de caracterización de partículas, como la cromatografía de exclusión por tamaño (SEC), la dispersión de luz dinámica (DLS) y la dispersión de luz electroforética (ELS).
Véase también
- Dispersión de luz estática diferencial (DSLS)
- Dispersión dinámica de la luz
- Dispersión de luz
- Interacciones proteína-proteína
Referencias
- ^ A. Einstein (1910). "Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes". Anales de Física . 33 (16): 1275. Código bibliográfico : 1910AnP...338.1275E. doi : 10.1002/andp.19103381612.
- ^ CV Raman (1927). "Relación del efecto Tyndall con la presión osmótica en soluciones coloidales". Indian J. Phys . 2 : 1.
- ^ P. Debye (1944). "Dispersión de luz en soluciones". J. Appl. Phys . 15 (4): 338. Código Bibliográfico :1944JAP....15..338D. doi :10.1063/1.1707436.
- ^ BH Zimm (1945). "Teoría molecular de la dispersión de la luz en fluidos". J. Chem. Phys . 13 (4): 141. Código Bibliográfico :1945JChPh..13..141Z. doi :10.1063/1.1724013.
- ^ ab BH Zimm (1948). "La dispersión de la luz y la función de distribución radial de soluciones de alto contenido en polímeros". J. Chem. Phys . 16 (12): 1093. Bibcode :1948JChPh..16.1093Z. doi :10.1063/1.1746738.
- ^ Hiemenz, Paul C.; Logia, Timothy P. (2007). Química de polímeros (2ª ed.). Boca Ratón, Florida [ua]: CRC Press. págs. 307–308. ISBN 978-1-57444-779-8.
- ^ "Medición de masa molecular mediante dispersión de luz estática :: Anton Paar Wiki". Anton Paar . Consultado el 23 de septiembre de 2022 .
- ^ Chang, Qing (2016), "Presión osmótica", Química coloidal e interfacial para el control de la calidad del agua , Elsevier, págs. 37-47, doi :10.1016/b978-0-12-809315-3.00004-9, ISBN 978-0-12-809315-3, consultado el 14 de junio de 2022
- ^ Schaetzel, K. (1991). "Supresión de la dispersión múltiple mediante técnicas de correlación cruzada de fotones". J. Mod. Opt . 38 : SA393–SA398. Código Bibliográfico :1990JPCM....2..393S. doi :10.1088/0953-8984/2/S/062. S2CID 250745836.
- ^ Urban, C.; Schurtenberger, P. (1998). "Caracterización de suspensiones coloidales turbias utilizando técnicas de dispersión de luz combinadas con métodos de correlación cruzada". J. Colloid Interface Sci . 207 (1): 150–158. Bibcode :1998JCIS..207..150U. doi :10.1006/jcis.1998.5769. PMID 9778402.
- ^ Block, I.; Scheffold, F. (2010). "Dispersión de luz modulada por correlación cruzada 3D: mejora de la caracterización de muestras turbias". Review of Scientific Instruments . 81 (12): 123107–123107–7. arXiv : 1008.0615 . Bibcode :2010RScI...81l3107B. doi :10.1063/1.3518961. PMID 21198014. S2CID 9240166.
- ^ Pusey, PN (1999). "Supresión de la dispersión múltiple mediante técnicas de correlación cruzada de fotones". Current Opinion in Colloid & Interface Science . 4 (3): 177–185. doi :10.1016/S1359-0294(99)00036-9.
- ^ Some, D. (2013). "Análisis de interacciones biomoleculares basado en dispersión de luz". Biophys. Rev . 5 (2): 147–158. doi :10.1007/s12551-013-0107-1. PMC 3641300 . PMID 23646069.
- ^ Sedlák, Marián (1 de marzo de 2006). "Estructura supramolecular a gran escala en soluciones de compuestos de baja masa molar y mezclas de líquidos: I. Caracterización de la dispersión de la luz". The Journal of Physical Chemistry B . 110 (9): 4329–4338. doi :10.1021/jp0569335. ISSN 1520-6106. PMID 16509731.
- ^ Díaz‐Lasprilla, Ana M.; Mercado, Ronald A.; Ramírez‐Caballero, Gustavo E. (20 de junio de 2021). "Efecto del grado de polimerización del glicerol en las propiedades emulsionantes de los ésteres de poliglicerol". Journal of Applied Polymer Science . 138 (24): 50566. doi :10.1002/app.50566. ISSN 0021-8995. S2CID 233888953.
- ^ "Dimerización de la albúmina sérica bovina según la medición del tamaño de partícula y la masa molecular :: Anton-Paar.com". Anton Paar . Consultado el 14 de junio de 2022 .
Enlaces externos
- Aplicación de la dispersión de luz estática
- Litesizer










