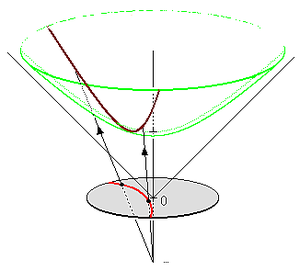
- El modelo hiperboloide se puede representar como la ecuación t 2 = x 1 2 + x 2 2 + 1 , t > 1 . Se puede utilizar para construir un modelo de disco de Poincaré como una proyección vista desde ( t = −1, x 1 = 0, x 2 = 0) , proyectando la mitad superior del hiperboloide sobre el disco unitario en t = 0 . La geodésica roja en el modelo de disco de Poincaré se proyecta sobre la geodésica marrón en el hiperboloide verde.
- Animación de un mosaico hiperbólico parcial {7,3} del hiperboloide rotado en la perspectiva de Poincaré.
Modelo de disco de Poincaré


En geometría , el modelo de disco de Poincaré , también llamado modelo de disco conforme , es un modelo de geometría hiperbólica bidimensional en el que todos los puntos están dentro del disco unitario y las líneas rectas son arcos circulares contenidos dentro del disco que son ortogonales al círculo unitario o diámetros del círculo unitario.
El grupo de isometrías que preservan la orientación del modelo de disco está dado por el grupo unitario especial proyectivo PSU(1,1) , el cociente del grupo unitario especial SU(1,1) por su centro { I , − I } .
Junto con el modelo de Klein y el modelo de semiespacio de Poincaré , fue propuesto por Eugenio Beltrami , quien utilizó estos modelos para demostrar que la geometría hiperbólica era equiconsistente con la geometría euclidiana . Recibe el nombre de Henri Poincaré , porque su redescubrimiento de esta representación catorce años después se hizo más conocido que el trabajo original de Beltrami. [1]
El modelo de bola de Poincaré es un modelo similar para la geometría hiperbólica tridimensional o n -dimensional en la que los puntos de la geometría están en la bola unitaria n -dimensional .
Historia
El modelo de disco fue descrito por primera vez por Bernhard Riemann en una conferencia de 1854 (publicada en 1868), que inspiró un artículo de 1868 de Eugenio Beltrami . [2] Henri Poincaré lo empleó en su tratamiento de 1882 de las funciones hiperbólicas, parabólicas y elípticas, [3] pero se hizo ampliamente conocido después de la presentación de Poincaré en su tratado filosófico de 1905, Ciencia e hipótesis . [4] Allí describe un mundo, ahora conocido como el disco de Poincaré, en el que el espacio era euclidiano, pero que parecía a sus habitantes satisfacer los axiomas de la geometría hiperbólica:
"Supongamos, por ejemplo, un mundo encerrado en una gran esfera y sujeto a las siguientes leyes: La temperatura no es uniforme; es máxima en su centro y disminuye gradualmente a medida que nos movemos hacia la circunferencia de la esfera, donde es el cero absoluto . La ley de esta temperatura es la siguiente: Si es el radio de la esfera y la distancia del punto considerado desde el centro, la temperatura absoluta será proporcional a . Además, supondré que en este mundo todos los cuerpos tienen el mismo coeficiente de dilatación , de modo que la dilatación lineal de cualquier cuerpo es proporcional a su temperatura absoluta. Finalmente, supondré que un cuerpo transportado de un punto a otro de diferente temperatura está instantáneamente en equilibrio térmico con su nuevo entorno. ... Si construyen una geometría, no será como la nuestra, que es el estudio de los movimientos de nuestros sólidos invariables; será el estudio de los cambios de posición que habrán distinguido así, y serán 'desplazamientos no euclidianos', y esto será geometría no euclidiana . Para que seres como nosotros, educados en un mundo así, no tengan la misma geometría que la nuestra.” [4] (pp.65-68)
El disco de Poincaré fue una pieza importante de evidencia para la hipótesis de que la elección de la geometría espacial es convencional más que fáctica, especialmente en las influyentes discusiones filosóficas de Rudolf Carnap [5] y de Hans Reichenbach . [6]
Líneas y distancias

Las líneas rectas hiperbólicas o geodésicas constan de todos los arcos de círculos euclidianos contenidos dentro del disco que son ortogonales al límite del disco, más todos los diámetros del disco.
Las distancias en este modelo son métricas de Cayley-Klein . Dados dos puntos distintos p y q dentro del disco, la única línea hiperbólica que los conecta interseca el límite en dos puntos ideales , a y b . Etiquételos de modo que los puntos sean, en orden, a , p , q , b , es decir, de modo que | aq | > | ap | y | pb | > | qb | .
La distancia hiperbólica entre p y q es entonces [7]
Las barras verticales indican la longitud euclidiana del segmento de línea que conecta los puntos entre sí en el modelo (no a lo largo del arco del círculo); ln es el logaritmo natural .
De manera equivalente, si u y v son dos vectores en un espacio vectorial real de n dimensiones R n con la norma euclidiana habitual, ambos con norma menor que 1, entonces podemos definir un invariante isométrico mediante
donde denota la norma euclidiana usual. Entonces la función de distancia es
Esta función de distancia se define para dos vectores cualesquiera de norma menor que uno, y convierte el conjunto de dichos vectores en un espacio métrico que es un modelo del espacio hiperbólico de curvatura constante −1. El modelo tiene la propiedad conforme de que el ángulo entre dos curvas que se intersecan en el espacio hiperbólico es el mismo que el ángulo en el modelo.
Especializándonos en el caso en el que uno de los puntos es el origen y la distancia euclidiana entre los puntos es r , la distancia hiperbólica es: donde es la función hiperbólica inversa de la tangente hiperbólica . Si los dos puntos se encuentran en el mismo radio y el punto se encuentra entre el origen y el punto , su distancia hiperbólica es Esto se reduce al caso especial anterior si .
Métrica y curvatura

El tensor métrico asociado del modelo de disco de Poincaré está dado por [8]
donde x i son las coordenadas cartesianas del espacio euclidiano ambiental.
Un marco ortonormal con respecto a esta métrica de Riemann está dado por
con doble cobastidor de 1 forma
En dos dimensiones
En dos dimensiones, con respecto a estos marcos y la conexión Levi-Civita , las formas de conexión están dadas por la única matriz antisimétrica de 1-formas que está libre de torsión , es decir, que satisface la ecuación matricial . Resolviendo esta ecuación se obtiene
donde está la matriz de curvatura
Por lo tanto, la curvatura del disco hiperbólico es
Construcción de líneas
Con compás y regla
La única línea hiperbólica que pasa por dos puntos y no por el diámetro del círculo límite se puede construir de la siguiente manera:
- Sea la inversión en el círculo límite del punto
- Sea la inversión en el círculo límite del punto
- Sea el punto medio del segmento
- Sea el punto medio del segmento
- Dibuje una línea perpendicular al segmento.
- Dibuje una línea perpendicular al segmento.
- sea donde línea y línea se cruzan.
- Dibujar un círculo con centro y pasando por (y ).
- La parte del círculo que está dentro del disco es la línea hiperbólica.
Si P y Q están en un diámetro del círculo límite, ese diámetro es la línea hiperbólica.
Otra forma es:
- Sea el punto medio del segmento
- Dibuje una línea m a través de la perpendicular al segmento
- Sea la inversión en el círculo límite del punto
- Sea el punto medio del segmento
- Dibuje una línea perpendicular al segmento.
- sea donde línea y línea se cruzan.
- Dibujar un círculo con centro y pasando por (y ).
- La parte del círculo que está dentro del disco es la línea hiperbólica.
Por geometría analítica
Una construcción básica de la geometría analítica es hallar una línea que pase por dos puntos dados. En el modelo del disco de Poincaré, las líneas en el plano están definidas por porciones de círculos que tienen ecuaciones de la forma
que es la forma general de un círculo ortogonal al círculo unitario, o bien por diámetros. Dados dos puntos u = (u 1 ,u 2 ) y v = (v 1 ,v 2 ) en el disco que no se encuentran en un diámetro, podemos resolver el círculo de esta forma que pasa por ambos puntos y obtener
Si los puntos u y v son puntos en el límite del disco que no se encuentran en los extremos de un diámetro, lo anterior se simplifica a
Anglos
Podemos calcular el ángulo entre el arco circular cuyos puntos finales ( puntos ideales ) están dados por los vectores unitarios u y v , y el arco cuyos puntos finales son s y t , mediante una fórmula. Como los puntos ideales son los mismos en el modelo de Klein y en el modelo del disco de Poincaré, las fórmulas son idénticas para cada modelo.
Si las líneas de ambos modelos son diámetros, de modo que v = − u y t = − s , entonces simplemente estamos encontrando el ángulo entre dos vectores unitarios, y la fórmula para el ángulo θ es
Si v = − u pero no t = − s , la fórmula se convierte, en términos del producto cuña ( ),
dónde
Si ambas cuerdas no son diámetros, se obtiene la fórmula general
dónde
Usando la identidad de Binet-Cauchy y el hecho de que estos son vectores unitarios, podemos reescribir las expresiones anteriores puramente en términos del producto escalar , como
Ciclos
En el plano euclidiano, los círculos generalizados (curvas de curvatura constante) son líneas y círculos. En la esfera , son círculos mayores y menores . En el plano hiperbólico, hay 4 tipos distintos de círculos o ciclos generalizados : círculos, horociclos, hiperciclos y geodésicas (o "líneas hiperbólicas"). En el modelo del disco de Poincaré, todos ellos están representados por líneas rectas o círculos.
Un círculo euclidiano:
- que esta completamente dentro del disco es un circulo hiperbólico ;
- que está dentro del disco y tangente al límite es un horociclo ;
- que interseca el límite ortogonalmente es una línea hiperbólica ; y
- que interseca el límite de forma no ortogonal es un hiperciclo .
Una cuerda euclidiana del círculo límite:
- que pasa por el centro es una línea hiperbólica; y
- que no pasa por el centro es un hiperciclo.
Círculos
Un círculo (el conjunto de todos los puntos de un plano que se encuentran a una distancia dada de un punto dado, su centro) es un círculo que se encuentra completamente dentro del disco y que no toca ni interseca su borde. El centro hiperbólico del círculo en el modelo no se corresponde en general con el centro euclidiano del círculo, sino que se encuentran en el mismo radio del disco de Poincaré. (El centro euclidiano siempre está más cerca del centro del disco que el centro hiperbólico).
Hiperciclos
Un hiperciclo (el conjunto de todos los puntos de un plano que están en un lado y a una distancia dada de una línea dada, su eje) es un arco de círculo euclidiano o cuerda del círculo límite que interseca el círculo límite en un ángulo positivo pero no recto . Su eje es la línea hiperbólica que comparte los mismos dos puntos ideales . Esto también se conoce como curva equidistante.
Horociclos

Un horociclo (una curva cuyas geodésicas normales o perpendiculares son paralelas límite , todas convergiendo asintóticamente al mismo punto ideal ), es un círculo dentro del disco que es tangente al círculo límite del disco. El punto donde toca el círculo límite no es parte del horociclo. Es un punto ideal y es el centro hiperbólico del horociclo. También es el punto al que convergen todas las geodésicas perpendiculares.
En el modelo del disco de Poincaré, los puntos euclidianos que representan los "extremos" opuestos de un horociclo convergen hacia su centro en el círculo límite, pero en el plano hiperbólico cada punto de un horociclo está infinitamente lejos de su centro, y los extremos opuestos del horociclo no están conectados. (La intuición euclidiana puede ser engañosa porque la escala del modelo aumenta hasta el infinito en el círculo límite).
Relación con otros modelos de geometría hiperbólica

Relación con el modelo de disco de Klein
El modelo de disco de Klein (también conocido como modelo de Beltrami-Klein) y el modelo de disco de Poincaré son modelos que proyectan todo el plano hiperbólico en un disco . Los dos modelos están relacionados a través de una proyección sobre o desde el modelo de hemisferio . El modelo de disco de Klein es una proyección ortográfica al modelo de hemisferio mientras que el modelo de disco de Poincaré es una proyección estereográfica .
Una ventaja del modelo de disco de Klein es que las líneas en este modelo son cuerdas rectas euclidianas . Una desventaja es que el modelo de disco de Klein no es conforme (los círculos y los ángulos están distorsionados).
Al proyectar las mismas líneas en ambos modelos sobre un disco, ambas líneas pasan por los mismos dos puntos ideales (los puntos ideales permanecen en el mismo lugar) además el polo de la cuerda en el modelo de disco de Klein es el centro del círculo que contiene el arco en el modelo de disco de Poincaré.
Un punto ( x , y ) en el modelo de disco de Poincaré se asigna a en el modelo de Klein.
Un punto ( x , y ) en el modelo de Klein se corresponde con el modelo de disco de Poincaré.
Para los puntos ideales y las fórmulas se vuelven así los puntos son fijos.
Si es un vector de norma menor que uno que representa un punto del modelo de disco de Poincaré, entonces el punto correspondiente del modelo de disco de Klein viene dado por:
Por el contrario, a partir de un vector de norma menor que uno que representa un punto del modelo de Beltrami-Klein, el punto correspondiente del modelo de disco de Poincaré viene dado por:
Relación con el modelo de semiplano de Poincaré
Tanto el modelo de disco de Poincaré como el modelo de semiplano de Poincaré llevan el nombre de Henri Poincaré .
Si es un número complejo de norma menor que uno que representa un punto del modelo del disco de Poincaré, entonces el punto correspondiente del modelo del semiplano viene dado por la inversa de la transformada de Cayley:
Un punto ( x , y ) en el modelo de disco se asigna al modelo de semiplano. [9]
Un punto ( x , y ) en el modelo de semiplano se asigna a un punto en el modelo de disco.
Relación con el modelo hiperboloide
El modelo del disco de Poincaré, así como el modelo de Klein , están relacionados con el modelo hiperboloide de forma proyectiva . Si tenemos un punto [ t , x 1 , ..., x n ] en la hoja superior del hiperboloide del modelo hiperboloide, definiendo así un punto en el modelo hiperboloide, podemos proyectarlo sobre el hiperplano t = 0 intersecándolo con una línea dibujada a través de [−1, 0, ..., 0]. El resultado es el punto correspondiente del modelo del disco de Poincaré.
Para las coordenadas cartesianas ( t , x i ) en el hiperboloide y ( y i ) en el plano, las fórmulas de conversión son:
Compare las fórmulas para la proyección estereográfica entre una esfera y un plano.
Realizaciones artísticas

MC Escher exploró el concepto de representar el infinito en un plano bidimensional. Las conversaciones con el matemático canadiense HSM Coxeter alrededor de 1956 inspiraron el interés de Escher en las teselaciones hiperbólicas , que son teselas regulares del plano hiperbólico. Los grabados en madera de Escher Circle Limit I–IV demuestran este concepto entre 1958 y 1960, siendo el último Circle Limit IV: Heaven and Hell en 1960. [10] Según Bruno Ernst, el mejor de ellos es Circle Limit III .
HyperRogue , un juego roguelike, utiliza el plano hiperbólico para la geometría de su mundo y también utiliza el modelo de disco de Poincaré.
Véase también
- Geometría hiperbólica
- Modelo de Beltrami-Klein
- Modelo de semiplano de Poincaré
- Métrica de Poincaré
- Pseudosfera
- Modelo hiperboloide
- Geometría inversa
- Teselación uniforme en el plano hiperbólico
Referencias
- ^ Penrose, Roger (2004). El camino a la realidad: una guía completa de las leyes del universo . Gran Bretaña: Jonathan Cape. p. 45. ISBN 0-224-04447-8.
- ^ Milnor, John W. "Geometría hiperbólica: los primeros 150 años". Boletín de la Sociedad Matemática Americana 6, núm. 1 (1982): 9-24.B. Riemann, "Ueber die Hypothesen welche der Geometrie zu Grunde liegen", Abh. KG Wiss. Göttingen 13 (de su discurso inaugural de 1854).
Eugenio Beltrami. "Teoria fundamentale degli spazii di curvatura costante", Annali di mat. ser. II 2, 232-255 (Op. Mat. 1, 406-429; Ann. École Norm. Sup. 6 (1869), 345-375).
- ^ Poincaré, H. (1 de diciembre de 1882). "Teoría de los grupos fuchsiens". Acta Mathematica (en francés). 1 (1): 1–62. doi : 10.1007/BF02592124 . ISSN 1871-2509. S2CID 120406828.
- ^ ab Poincaré, Henri (1905). Ciencia e hipótesis. Robarts - Universidad de Toronto. Londres W. Scott.
- ^ Carus, A. W.; Friedman, Michael; Kienzler, Wolfgang; Richardson, Alan; Schlotter, Sven (25 de junio de 2019). Rudolf Carnap: Primeros escritos: Las obras completas de Rudolf Carnap, volumen 1. Oxford University Press. ISBN 978-0-19-106526-2.
- ^ Reichenbach, Hans (13 de marzo de 2012). La filosofía del espacio y el tiempo. Courier Corporation. ISBN 978-0-486-13803-9.
- ^ Berger, Marcel (1987) [1977]. "9.6 El modelo de Poincaré". Geometría II . Traducido por Cole, M.; Levy, S. Springer. pág. 339.
- ^ "Comparación de los tensores métricos de los modelos de geometría hiperbólica de disco de Poincaré y de Klein". Stack Exchange . 23 de mayo de 2015.
- ^ "Asignación del modelo de disco de Poincaré al modelo de semiplano de Poincaré" . Consultado el 13 de diciembre de 2015 .
- ^ Exploración del límite del círculo de Escher
Lectura adicional
- James W. Anderson, Geometría hiperbólica , segunda edición, Springer, 2005.
- Eugenio Beltrami, Teoria fundamentale degli spazii di curvatura costante , Annali. di Mat., ser II 2 (1868), 232–255.
- Saul Stahl, El semiplano de Poincaré , Jones y Bartlett, 1993.



































![{\displaystyle {\begin{alineado}x^{2}+y^{2}&{}+{\frac {u_{2}(v_{1}^{2}+v_{2}^{2} +1)-v_{2}(u_{1}^{2}+u_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}} x\\[8pt]&{}+{\frac {v_{1}(u_{1}^{2}+u_{2}^{2}+1)-u_{1}(v_{1}^ {2}+v_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/16afa80f4b34b6bd195672537bd9b6844fad533c)