Modelo de semiplano de Poincaré

En geometría no euclidiana , el modelo de semiplano de Poincaré es una forma de representar el plano hiperbólico utilizando puntos en el conocido plano euclidiano . En concreto, cada punto del plano hiperbólico se representa utilizando un punto euclidiano con coordenadas ⁠ ⁠${\displaystyle \langle x,y\rangle }$ cuya ⁠ ⁠${\estilo de visualización y}$ coordenada es mayor que cero, el semiplano superior , y se adopta un tensor métrico (definición de distancia) llamado métrica de Poincaré , en el que la escala local es inversamente proporcional a la ⁠ ⁠${\estilo de visualización y}$ coordenada. Los puntos en el eje ⁠ ⁠${\estilo de visualización x}$ , cuya ⁠ ⁠${\estilo de visualización y}$ coordenada es igual a cero, representan puntos ideales (puntos en el infinito), que están fuera del plano hiperbólico propiamente dicho.

A veces se considera que los puntos del modelo de semiplano se encuentran en el plano complejo con parte imaginaria positiva . Con esta interpretación, cada punto del plano hiperbólico se asocia a un número complejo .

El modelo de semiplano puede ser pensado como una proyección cartográfica desde el plano hiperbólico curvo al plano euclidiano plano. A partir del modelo hiperboloide (una representación del plano hiperbólico sobre un hiperboloide de dos láminas incrustadas en el espacio tridimensional de Minkowski , análogo a la esfera incrustada en el espacio tridimensional euclidiano), el modelo de semiplano se obtiene por proyección ortográfica en una dirección paralela a un vector nulo , que también puede ser pensado como una especie de proyección estereográfica centrada en un punto ideal. La proyección es conforme , es decir, conserva los ángulos, y al igual que la proyección estereográfica de la esfera proyecta círculos generalizados ( geodésicas , hiperciclos , horociclos y círculos) en el plano hiperbólico a círculos generalizados (líneas o círculos) en el plano. En particular, las geodésicas (análogas a las líneas rectas ) se proyectan sobre semicírculos cuyo centro tiene la coordenada${\estilo de visualización y}$ cero, o sobre líneas rectas verticales de coordenada constante , los${\estilo de visualización x}$ hiperciclos se proyectan sobre círculos que cruzan el eje ,${\estilo de visualización x}$ los horociclos se proyectan sobre círculos tangentes al eje${\estilo de visualización x}$ o sobre líneas horizontales de coordenada constante , y ${\estilo de visualización y}$los círculos se proyectan sobre círculos contenidos enteramente en el semiplano.

Los movimientos hiperbólicos , las transformaciones geométricas que preservan la distancia desde el plano hiperbólico hacia sí mismo, se representan en el semiplano de Poincaré por el subconjunto de transformaciones de Möbius del plano que preservan el semiplano; estas son transformaciones conformes que preservan el círculo y que envían el eje ⁠ ⁠${\estilo de visualización x}$ hacia sí mismo sin cambiar su orientación. Cuando los puntos en el plano se toman como números complejos, cualquier transformación de Möbius se representa por una transformación fraccionaria lineal de números complejos, y los movimientos hiperbólicos se representan por elementos del grupo lineal especial proyectivo ⁠ ⁠${\displaystyle \operatorname {PSL} _{2}(\mathbb {R} )}$ .

La transformada de Cayley proporciona una isometría entre el modelo de semiplano y el modelo de disco de Poincaré , que es una proyección estereográfica del hiperboloide centrado en cualquier punto ordinario en el plano hiperbólico, que mapea el plano hiperbólico sobre un disco en el plano euclidiano, y también comparte las propiedades de conformidad y mapeo de círculos generalizados a círculos generalizados.

El modelo de semiplano de Poincaré debe su nombre a Henri Poincaré , pero se originó con Eugenio Beltrami , quien lo utilizó, junto con el modelo de Klein y el modelo de disco de Poincaré , para demostrar que la geometría hiperbólica era equiconsistente con la geometría euclidiana .

El modelo de semiplano se puede generalizar al modelo de semiespacio de Poincaré del espacio hiperbólico dimensional reemplazando${\estilo de visualización (n+1)}$ la coordenada única por coordenadas distintas .${\estilo de visualización x}$${\estilo de visualización n}$

La métrica del modelo en el semiplano, es:${\displaystyle \{\langle x,y\rangle \mid y>0\},}$

${\displaystyle (ds)^{2}={\frac {(dx)^{2}+(dy)^{2}}{y^{2}}}}$

donde s mide la longitud a lo largo de una línea (posiblemente curva). Las líneas rectas en el plano hiperbólico ( geodésicas para este tensor métrico, es decir, curvas que minimizan la distancia) se representan en este modelo mediante arcos circulares perpendiculares al eje x (semicírculos cuyos centros están en el eje x ) y rayos rectos verticales perpendiculares al eje x .

Si y son dos puntos en el semiplano y es la reflexión de a través del eje x en el semiplano inferior, la distancia entre los dos puntos bajo la métrica del plano hiperbólico es:${\textstyle p_{1}=\langle x_{1},y_{1}\rangle }$${\textstyle p_{2}=\langle x_{2},y_{2}\rangle }$${\textstyle y>0}$${\textstyle {\tilde {p}}_{1}=\langle x_{1},-y_{1}\rangle }$${\textstyle p_{1}}$

$${\displaystyle {\begin{aligned}\operatorname {dist} (p_{1},p_{2})&=2\operatorname {arsinh} {\frac {\|p_{2}-p_{1}\|}{2{\sqrt {y_{1}y_{2}{\vphantom {t}}}}}}\\[10mu]&=2\operatorname {artanh} {\frac {\|p_{2}-p_{1}\|}{\|p_{2}-{\tilde {p}}_{1}\|}}\\[10mu]&=2\ln {\frac {\|p_{2}-p_{1}\|+\|p_{2}-{\tilde {p}}_{1}\|}{2{\sqrt {y_{1}y_{2}{\vphantom {t}}}}},\end{aligned}}}$$

donde es la distancia euclidiana entre los puntos ⁠ ⁠ y ⁠ ⁠ , es el seno hiperbólico inverso y es la tangente hiperbólica inversa . Se puede pensar que esta fórmula proviene de la longitud de la cuerda en la métrica de Minkowski entre puntos en el modelo hiperboloide , , análoga a encontrar la longitud de arco en una esfera en términos de la longitud de la cuerda. Se puede pensar que esta fórmula proviene de la distancia euclidiana en el modelo del disco de Poincaré con un punto en el origen, análoga a encontrar la longitud de arco en la esfera tomando una proyección estereográfica centrada en un punto y midiendo la distancia euclidiana en el plano desde el origen hasta el otro punto.${\textstyle \|p_{2}-p_{1}\|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{ 2}}}}$$estilo de visualización p_{1}}$$estilo de visualización p_{2}$${\displaystyle {\vphantom {\Big )}}\nombre del operador {arsinh} x={}}$${\displaystyle \textstyle \ln {\bigl (}x+{\sqrt {x^{2}+1}}{\bigr )}}$${\displaystyle \operatorname {artanh} x{\vphantom {\big )}}={}}$${\displaystyle {\frac {1}{2}}\ln {\bigl (}(1+x)/(1-x){\bigr )}}$${\textstyle 2\operatorname {arsinh} }$${\displaystyle \operatorname {acorde} (p_{1},\,p_{2})={}{\vphantom {\tfrac {1}{2}}}}$${\displaystyle 2\sinh {\tfrac {1}{2}}\nombre del operador {dist} (p_{1},\,p_{2})}$${\textstyle 2\operatorname {artanh} }$

Si los dos puntos y están en una línea hiperbólica (semicírculo euclidiano) que interseca el eje x en los puntos ideales y la distancia de a es:${\textstyle p_{1}}$${\textstyle p_{2}}$${\textstyle p_{0}=\langle x_{0},0\rangle }$${\textstyle p_{3}=\langle x_{3},0\rangle,}$${\textstyle p_{1}}$${\textstyle p_{2}}$

$${\displaystyle \operatorname {dist} (p_{1},p_{2})=\left|\,\ln {\frac {\|p_{2}-p_{0}\|\|p_{1}-p_{3}\|}{\|p_{1}-p_{0}\|\|p_{2}-p_{3}\|}}\right|.}$$

Cf. Relación cruzada .

Algunos casos especiales se pueden simplificar. Dos puntos con la misma coordenada :${\displaystyle x}$ [ ^1]

$${\displaystyle {\operatorname {dist} }{\bigl (}\langle x,y_{1}\rangle ,\langle x,y_{2}\rangle {\bigr )}=\left|\,\ln {\frac {y_{2}}{y_{1}}}\right|=|\ln y_{2}-\ln y_{1}|.}$$

Dos puntos con la misma coordenada:${\textstyle y}$

$${\displaystyle {\operatorname {dist} }{\bigl (}\langle x_{1},\,y\rangle ,\langle x_{2},\,y\rangle {\bigr )}=2\operatorname {arsinh} {\frac {|x_{2}-x_{1}|}{2y}}.}$$

Un punto ⁠ ⁠${\displaystyle \langle x_{1},r\rangle }$ en el vértice del semicírculo y otro punto en un ángulo central de ⁠ ⁠ .${\textstyle (x-x_{1})^{2}+y^{2}=r^{2},}$${\displaystyle \phi }$

$${\displaystyle {\operatorname {dist} }{\bigl (}\langle x_{1},r\rangle ,\langle x_{1}\pm r\sin \phi ,r\cos \phi \rangle {\bigr )}={2\operatorname {artanh} }{\bigl (}{\tan {\tfrac {1}{2}}\phi }{\bigr )}=\operatorname {gd} ^{-1}\phi ,}$$

donde ⁠ ⁠ es la ${\displaystyle \textstyle \operatorname {gd} ^{-1}}$función Gudermanniana inversa .

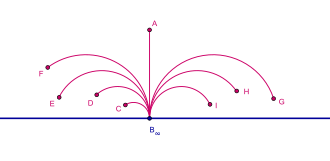
Los puntos ideales (puntos en el infinito) en el modelo del semiplano de Poincaré son de dos tipos: los puntos en el eje ⁠ ⁠${\displaystyle x}$ y un punto imaginario enel que se encuentra el punto ideal al que convergen todas las líneas ortogonales al eje ⁠ ⁠ .${\displaystyle y=\infty }$${\displaystyle x}$

Las líneas rectas , las geodésicas (el camino más corto entre los puntos contenidos en ellas) se modelan mediante semicírculos cuyo origen está en el eje x, o bien mediante rayos rectos verticales ortogonales al eje x.

Un círculo (curva equidistante de un punto central) con centro y radio está modelado por un círculo con centro ⁠ ⁠ y radio ⁠ ⁠ .${\displaystyle \langle x,y\rangle }$${\displaystyle r}$${\displaystyle \langle x,y\cosh r\rangle }$${\displaystyle y\sinh r}$

Un hiperciclo (una curva equidistante de una línea recta, su eje) se modela mediante un arco circular que interseca el eje ⁠ ⁠${\displaystyle x}$ en los mismos dos puntos ideales que el semicírculo que modela su eje pero en un ángulo agudo u obtuso , o una línea recta que interseca el eje ⁠ ⁠ en el mismo punto que la línea vertical que modela su eje, pero en un ${\displaystyle x}$ángulo agudo u obtuso .

Un horociclo (una curva cuyas normales convergen todas asintóticamente en la misma dirección, su centro) se modela mediante un círculo tangente al eje ⁠ ⁠${\displaystyle x}$ (pero excluyendo el punto ideal de intersección, que es su centro), o una línea paralela al eje ⁠ ⁠${\displaystyle x}$ , en cuyo caso el centro es el punto ideal en ⁠ ⁠${\displaystyle y=\infty }$ .

Un círculo euclidiano con centro y radio representa: ${\displaystyle \langle x_{e},y_{e}\rangle }$${\displaystyle r_{e}}$

• Cuando el círculo está completamente dentro del semiplano, un círculo hiperbólico con centro y radio.$${\displaystyle \textstyle {\big \langle }x_{e},{\sqrt {y_{e}^{2}-r_{e}^{2}}}\,{\big \rangle }}$$$${\displaystyle {\tfrac {1}{2}}\ln \left({\frac {y_{e}+r_{e}}{y_{e}-r_{e}}}\right).}$$
• Cuando el círculo está completamente dentro del semiplano y toca el límite, se forma un horociclo centrado alrededor del punto ideal.${\displaystyle (x_{e},0)}$
• cuando el círculo interseca el límite ortogonalmente una línea hiperbólica${\displaystyle (y_{e}=0)}$
• cuando el círculo interseca el límite no ortogonal se forma un hiperciclo.

A continuación se muestra cómo se pueden utilizar construcciones con compás y regla en el modelo para lograr el efecto de las construcciones básicas en el plano hiperbólico . ^[2] Por ejemplo, cómo construir el semicírculo en el semiplano euclidiano que modela una línea en el plano hiperbólico a través de dos puntos dados.

Dibuje el segmento de línea entre los dos puntos. Construya la mediatriz del segmento de línea. Halle su intersección con el eje x . Dibuje el círculo alrededor de la intersección que pasa por los puntos dados. Borre la parte que está sobre o debajo del eje x .

O en el caso especial donde los dos puntos dados se encuentran en una línea vertical, dibuje esa línea vertical a través de los dos puntos y borre la parte que está sobre o debajo del eje x .

Si los dos puntos no están en una línea vertical: Dibuje la línea radial (semicírculo) entre los dos puntos dados como en el caso anterior. Construya una tangente a esa línea en el punto no central. Trace una perpendicular desde el punto central dado hasta el eje x . Encuentre la intersección de estas dos líneas para obtener el centro del círculo modelo. Dibuje el círculo modelo alrededor de ese nuevo centro y pasando por el punto no central dado.

Si los dos puntos dados se encuentran sobre una línea vertical y el centro dado está por encima del otro punto dado: Dibuje un círculo alrededor de la intersección de la línea vertical y el eje x que pase por el punto central dado. Dibuje una línea horizontal a través del punto no central. Construya la tangente al círculo en su intersección con esa línea horizontal. El punto medio entre la intersección de la tangente con la línea vertical y el punto no central dado es el centro del círculo modelo. Dibuje el círculo modelo alrededor de ese nuevo centro y pasando por el punto no central dado.

Si los dos puntos dados se encuentran sobre una línea vertical y el centro dado está debajo del otro punto dado: Dibuje un círculo alrededor de la intersección de la línea vertical y el eje x que pase por el punto central dado. Dibuje una línea tangente al círculo que pase por el punto no central dado. Dibuje una línea horizontal a través de ese punto de tangencia y encuentre su intersección con la línea vertical. El punto medio entre esa intersección y el punto no central dado es el centro del círculo modelo. Dibuje el círculo modelo alrededor de ese nuevo centro y que pase por el punto no central dado.

Traza una perpendicular p desde el centro euclidiano del círculo hasta el eje x . Sea q la intersección de esta línea con el eje x . Traza una línea tangente al círculo que pase por q . Traza el semicírculo h con centro q que pase por el punto donde se encuentran la tangente y el círculo. El centro (hiperbólico) es el punto donde h y p se cruzan. ^[3]

Creando el punto que es la intersección de dos líneas existentes, si se intersecan: Encuentra la intersección de los dos semicírculos (o líneas verticales) dados.

Creando uno o dos puntos en la intersección de una línea y un círculo (si se intersecan): Encuentra la intersección del semicírculo dado (o línea vertical) con el círculo dado.

Creando uno o dos puntos en la intersección de dos círculos (si se intersecan): Encuentra la intersección de los dos círculos dados.

El grupo proyectivo lineal PGL(2, C ) actúa sobre la esfera de Riemann mediante las transformaciones de Möbius . El subgrupo que proyecta el semiplano superior, H , sobre sí mismo es PSL(2, R ), las transformadas con coeficientes reales, y éstas actúan transitiva e isométricamente sobre el semiplano superior, convirtiéndolo en un espacio homogéneo .

Hay cuatro grupos de Lie estrechamente relacionados que actúan en el semiplano superior mediante transformaciones lineales fraccionarias y preservan la distancia hiperbólica.

• El grupo lineal especial SL(2, R ) que consiste en el conjunto de matrices 2×2 con elementos reales cuyo determinante es +1. Nótese que muchos textos (incluida Wikipedia) a menudo dicen SL(2, R ) cuando en realidad quieren decir PSL(2, R ).
• El grupo S*L(2, R ) está formado por el conjunto de matrices 2×2 con elementos reales cuyo determinante es +1 o −1. Nótese que SL(2, R ) es un subgrupo de este grupo.
• El grupo lineal especial proyectivo PSL(2, R ) = SL(2, R )/{± I }, que consiste en las matrices en SL(2, R ) módulo más o menos la matriz identidad.
• El grupo PS ^* L(2, R ) = S ^* L(2, R )/{± I }=PGL(2, R ) es nuevamente un grupo proyectivo, y nuevamente, módulo más o menos la matriz identidad. PSL(2, R ) está contenido como un subgrupo normal de índice dos, siendo la otra clase lateral el conjunto de matrices 2×2 con entradas reales cuyo determinante es igual a −1, módulo más o menos la matriz identidad.

La relación de estos grupos con el modelo de Poincaré es la siguiente:

• El grupo de todas las isometrías de H , a veces denotado como Isom( H ), es isomorfo a PS ^* L(2, R ). Esto incluye tanto las isometrías que preservan la orientación como las que la invierten. La función que invierte la orientación (la función especular) es .${\displaystyle z\rightarrow -{\overline {z}}}$
• El grupo de isometrías que preservan la orientación de H , a veces denominado Isom ⁺ ( H ), es isomorfo a PSL(2, R ).

Los subgrupos importantes del grupo de isometría son los grupos fucsianos .

También se ve con frecuencia el grupo modular SL(2, Z ). Este grupo es importante de dos maneras. Primero, es un grupo de simetría de la red cuadrada de puntos 2x2. Por lo tanto, las funciones que son periódicas en una cuadrícula cuadrada, como las formas modulares y las funciones elípticas , heredarán una simetría SL(2, Z ) de la cuadrícula. En segundo lugar, SL(2, Z ) es, por supuesto, un subgrupo de SL(2, R ), y por lo tanto tiene un comportamiento hiperbólico incorporado. En particular, SL(2, Z ) se puede utilizar para teselar el plano hiperbólico en celdas de área igual (de Poincaré).

La acción grupal del grupo lineal especial proyectivo sobre se define por${\displaystyle {\rm {PSL}}(2,\mathbb {R} )}$${\displaystyle \mathbb {H} }$

${\displaystyle {\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}\cdot z={\frac {az+b}{cz+d}}={\frac {(ac|z|^{2}+bd+(ad+bc)\Re (z))+i(ad-bc)\Im (z)}{|cz+d|^{2}}}.}$

Nótese que la acción es transitiva : para cualquier , existe un tal que . También es fiel, en el sentido de que si para todo entonces g = e .${\displaystyle z_{1},z_{2}\in \mathbb {H} }$${\displaystyle g\in {\rm {PSL}}(2,\mathbb {R} )}$${\displaystyle gz_{1}=z_{2}}$${\displaystyle gz=z}$${\displaystyle z\in \mathbb {H} ,}$

El subgrupo estabilizador o de isotropía de un elemento es el conjunto de los cuales dejan z inalterado: gz = z . El estabilizador de i es el grupo de rotación${\displaystyle z\in \mathbb {H} }$${\displaystyle g\in {\rm {PSL}}(2,\mathbb {R} )}$

${\displaystyle {\rm {SO}}(2)=\left.\left\{{\begin{pmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{pmatrix}}\right|\theta \in \mathbb {R} \right\}.}$

Dado que cualquier elemento se asigna a i por algún elemento de , esto significa que el subgrupo de isotropía de cualquier z es isomorfo a SO(2). Por lo tanto, . Alternativamente, el fibrado de vectores tangentes de longitud unitaria en el semiplano superior, llamado fibrado tangente unitario , es isomorfo a .${\displaystyle z\in \mathbb {H} }$${\displaystyle {\rm {PSL}}(2,\mathbb {R} )}$${\displaystyle \mathbb {H} ={\rm {PSL}}(2,\mathbb {R} )/{\rm {SO}}(2)}$${\displaystyle {\rm {PSL}}(2,\mathbb {R} )}$

El semiplano superior está teselado en conjuntos regulares libres por el grupo modular ${\displaystyle {\rm {SL}}(2,\mathbb {Z} ).}$

Las geodésicas de este tensor métrico son arcos circulares perpendiculares al eje real (semicírculos cuyo origen está en el eje real) y líneas rectas verticales que terminan en el eje real.

La geodésica de velocidad unitaria que sube verticalmente a través del punto i está dada por

${\displaystyle \gamma (t)={\begin{pmatrix}e^{t/2}&0\\0&e^{-t/2}\\\end{pmatrix}}\cdot i=ie^{t}.}$

Como PSL(2, R ) actúa transitivamente por isometrías del semiplano superior, esta geodésica se proyecta en las otras geodésicas a través de la acción de PSL(2, R ). Por lo tanto, la geodésica de velocidad unitaria general está dada por

${\displaystyle \gamma (t)={\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}{\begin{pmatrix}e^{t/2}&0\\0&e^{-t/2}\\\end{pmatrix}}\cdot i={\frac {aie^{t}+b}{cie^{t}+d}}.}$

Esto proporciona una descripción básica del flujo geodésico en el fibrado tangente de longitud unitaria ( fibrado lineal complejo ) en el semiplano superior. A partir de este modelo, se puede obtener el flujo en superficies de Riemann arbitrarias , como se describe en el artículo sobre el flujo de Anosov .

La métrica del modelo en el semiespacio está dada por${\textstyle \{\langle x,y,z\rangle \mid z>0\}}$

$${\displaystyle (ds)^{2}={\frac {(dx)^{2}+(dy)^{2}+(dz)^{2}}{z^{2}}}\,}$$

donde s mide la longitud a lo largo de una línea posiblemente curva. Las líneas rectas en el espacio hiperbólico ( geodésicas para este tensor métrico, es decir, curvas que minimizan la distancia) se representan en este modelo mediante arcos circulares normales al plano z = 0 (semicírculos cuyo origen está en el plano z = 0 ) y rayos verticales rectos normales al plano z = 0 .

La distancia entre dos puntos medida en esta métrica a lo largo de dicha geodésica es:${\textstyle p_{1}=\langle x_{1},y_{1},z_{1}\rangle }$${\textstyle p_{2}=\langle x_{2},y_{2},z_{2}\rangle }$

$${\displaystyle \operatorname {dist} (p_{1},p_{2})=2\operatorname {arsinh} {\frac {\|p_{2}-p_{1}\|}{2{\sqrt {z_{1}z_{2}{\vphantom {t}}}}}}.}$$

Este modelo se puede generalizar para modelar un espacio hiperbólico dimensional reemplazando el número real x por un vector en un espacio vectorial euclidiano de n dimensiones.${\displaystyle n+1}$

Notas

Fuentes