Dipolo

En física , un dipolo (del griego antiguo δίς ( dís )  'dos ​​veces' y πόλος ( pólos )  'eje') ^{[1] [2] [3]} es un fenómeno electromagnético que ocurre de dos maneras:

• Un dipolo eléctrico se encarga de la separación de las cargas eléctricas positivas y negativas que se encuentran en cualquier sistema electromagnético. Un ejemplo sencillo de este sistema es un par de cargas de igual magnitud pero de signo opuesto separadas por una distancia normalmente pequeña. (Un dipolo eléctrico permanente se denomina electreto ).
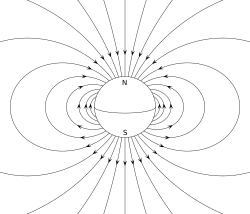
• Un dipolo magnético es la circulación cerrada de un sistema de corriente eléctrica . Un ejemplo sencillo es un solo bucle de cable con corriente constante a través de él. Un imán de barra es un ejemplo de un imán con un momento dipolar magnético permanente . ^{[4] [5]}

Los dipolos, ya sean eléctricos o magnéticos, se pueden caracterizar por su momento dipolar, una cantidad vectorial. En el caso del dipolo eléctrico simple, el momento dipolar eléctrico apunta de la carga negativa hacia la carga positiva y tiene una magnitud igual a la fuerza de cada carga multiplicada por la separación entre las cargas. (Para ser precisos: para la definición del momento dipolar, siempre se debe considerar el "límite dipolar", donde, por ejemplo, la distancia de las cargas generadoras debe converger a 0 mientras que, simultáneamente, la fuerza de la carga debe divergir hacia el infinito de tal manera que el producto permanezca como una constante positiva).

Para el bucle de corriente magnética (dipolar), el momento dipolar magnético apunta a través del bucle (de acuerdo con la regla de agarre de la mano derecha ), con una magnitud igual a la corriente en el bucle multiplicada por el área del bucle.

De manera similar a los bucles de corriente magnética, la partícula electrónica y algunas otras partículas fundamentales tienen momentos dipolares magnéticos, ya que un electrón genera un campo magnético idéntico al generado por un bucle de corriente muy pequeño. Sin embargo, el momento dipolar magnético de un electrón no se debe a un bucle de corriente, sino a una propiedad intrínseca del electrón. ^[6] El electrón también puede tener un momento dipolar eléctrico , aunque esto aún no se ha observado (ver momento dipolar eléctrico del electrón ).

Un imán permanente, como un imán de barra, debe su magnetismo al momento dipolar magnético intrínseco del electrón. Los dos extremos de un imán de barra se denominan polos (no deben confundirse con los monopolos , consulte la Clasificación a continuación) y pueden etiquetarse como "norte" y "sur". En términos del campo magnético de la Tierra, son respectivamente polos "en busca del norte" y "en busca del sur": si el imán estuviera suspendido libremente en el campo magnético de la Tierra, el polo en busca del norte apuntaría hacia el norte y el polo en busca del sur apuntaría hacia el sur. El momento dipolar del imán de barra apunta desde su sur magnético a su polo norte magnético . En una brújula magnética , el polo norte de un imán de barra apunta al norte. Sin embargo, eso significa que el polo norte geomagnético de la Tierra es el polo sur (polo en busca del sur) de su momento dipolar y viceversa.

Los únicos mecanismos conocidos para la creación de dipolos magnéticos son los bucles de corriente o el espín mecánico-cuántico, ya que la existencia de monopolos magnéticos nunca ha sido demostrada experimentalmente.

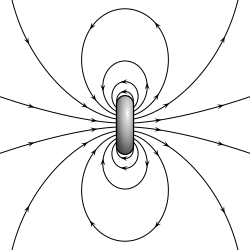
Un dipolo físico está formado por dos cargas puntuales iguales y opuestas: en sentido literal, dos polos. Su campo a grandes distancias (es decir, distancias grandes en comparación con la separación de los polos) depende casi por completo del momento dipolar, tal como se definió anteriormente. Un dipolo puntual (eléctrico) es el límite que se obtiene dejando que la separación tienda a cero mientras se mantiene fijo el momento dipolar. El campo de un dipolo puntual tiene una forma particularmente simple, y el término de orden 1 en la expansión multipolar es precisamente el campo del dipolo puntual.

Aunque no se conocen monopolos magnéticos en la naturaleza, sí existen dipolos magnéticos en forma de espín mecánico-cuántico asociado a partículas como los electrones (aunque la descripción precisa de tales efectos queda fuera del electromagnetismo clásico). Un dipolo puntual magnético teórico tiene un campo magnético exactamente de la misma forma que el campo eléctrico de un dipolo puntual eléctrico. Un bucle muy pequeño que transporta corriente es aproximadamente un dipolo puntual magnético; el momento dipolar magnético de un bucle de este tipo es el producto de la corriente que fluye en el bucle y el área (vectorial) del bucle.

Cualquier configuración de cargas o corrientes tiene un "momento dipolar", que describe el dipolo cuyo campo es la mejor aproximación, a grandes distancias, al de la configuración dada. Este es simplemente un término en la expansión multipolar cuando la carga total ("momento monopolar") es 0, como siempre lo es para el caso magnético, ya que no hay monopolos magnéticos. El término dipolar es el dominante a grandes distancias: su campo disminuye en proporción a ⁠1/r3^​⁠ , en comparación con ⁠1/r4^​⁠ para el siguiente término ( cuadrupolo ) y potencias superiores de ⁠1/a⁠ para términos más altos, o ⁠1/r2^​⁠ para el término monopolar.

Muchas moléculas tienen momentos dipolares de este tipo debido a distribuciones no uniformes de cargas positivas y negativas en los distintos átomos. Tal es el caso de los compuestos polares como el fluoruro de hidrógeno (HF), donde la densidad electrónica se comparte de manera desigual entre los átomos. Por lo tanto, el dipolo de una molécula es un dipolo eléctrico con un campo eléctrico inherente que no debe confundirse con un dipolo magnético , que genera un campo magnético.

El químico físico Peter JW Debye fue el primer científico en estudiar extensamente los dipolos moleculares y, como consecuencia, los momentos dipolares se miden en la unidad no perteneciente al SI llamada Debye en su honor.

Para las moléculas existen tres tipos de dipolos:

Dipolos permanentes

Estos ocurren cuando dos átomos en una molécula tienen electronegatividades sustancialmente diferentes  : un átomo atrae electrones más que otro, volviéndose más negativo, mientras que el otro átomo se vuelve más positivo. Una molécula con un momento dipolar permanente se denomina molécula polar . Véase atracciones dipolo-dipolo .

Dipolos instantáneos

Estos se producen por casualidad cuando los electrones están más concentrados en un lugar que en otro de una molécula , lo que crea un dipolo temporal. Estos dipolos son de menor magnitud que los dipolos permanentes, pero aún desempeñan un papel importante en la química y la bioquímica debido a su prevalencia. Véase dipolo instantáneo .

Dipolos inducidos

Estos fenómenos pueden ocurrir cuando una molécula con un dipolo permanente repele los electrones de otra molécula, lo que induce un momento dipolar en esa molécula. Una molécula está polarizada cuando lleva un dipolo inducido. Véase atracción dipolar inducida .

En términos más generales, un dipolo inducido de cualquier distribución de carga polarizable ρ (recuerde que una molécula tiene una distribución de carga) es causado por un campo eléctrico externo a ρ . Este campo puede, por ejemplo, originarse a partir de un ion o molécula polar en la proximidad de ρ o puede ser macroscópico (por ejemplo, una molécula entre las placas de un condensador cargado ). El tamaño del momento dipolar inducido es igual al producto de la fuerza del campo externo y la polarizabilidad dipolar de ρ .

Los valores del momento dipolar se pueden obtener midiendo la constante dieléctrica . Algunos valores típicos de la fase gaseosa que se dan con la unidad Debye son: ^[7]

• dióxido de carbono : 0
• Monóxido de carbono : 0,112 D
• ozono : 0,53 D
• fosgeno : 1,17 D
• amoniaco : 1,42 D
• vapor de agua : 1,85 D
• cianuro de hidrógeno : 2,98 D
• cianamida : 4,27 D
• bromuro de potasio : 10,41 D

El bromuro de potasio (KBr) tiene uno de los momentos dipolares más altos porque es un compuesto iónico que existe como molécula en fase gaseosa.

El momento dipolar total de una molécula puede aproximarse como una suma vectorial de los momentos dipolares de los enlaces . Como suma vectorial, depende de la orientación relativa de los enlaces, de modo que a partir del momento dipolar se puede deducir información sobre la geometría molecular .

Por ejemplo, el dipolo cero del CO ₂ implica que los dos momentos dipolares de enlace C=O se cancelan, de modo que la molécula debe ser lineal. En el caso del H ₂ O, los momentos dipolares de enlace O−H no se cancelan porque la molécula está doblada. En el caso del ozono (O ₃ ), que también es una molécula doblada, los momentos dipolares de enlace no son cero, aunque los enlaces O−O se den entre átomos similares. Esto concuerda con las estructuras de Lewis para las formas de resonancia del ozono, que muestran una carga positiva en el átomo de oxígeno central.

Un ejemplo en química orgánica del papel de la geometría en la determinación del momento dipolar son los isómeros cis y trans del 1,2-dicloroeteno . En el isómero cis , los dos enlaces polares C−Cl están en el mismo lado del doble enlace C=C y el momento dipolar molecular es 1,90 D. En el isómero trans , el momento dipolar es cero porque los dos enlaces C−Cl están en lados opuestos del C=C y se cancelan (y los dos momentos de enlace para los enlaces C−H mucho menos polares también se cancelan).

Otro ejemplo del papel de la geometría molecular es el trifluoruro de boro , que tiene tres enlaces polares con una diferencia de electronegatividad mayor que el umbral tradicionalmente citado de 1,7 para el enlace iónico . Sin embargo, debido a la distribución triangular equilátera de los iones fluoruro centrados en el catión boro y en el mismo plano que este, la simetría de la molécula hace que su momento dipolar sea cero.

Consideremos una colección de N partículas con cargas q _i y vectores de posición r _i . Por ejemplo, esta colección puede ser una molécula formada por electrones, todos con carga − e , y núcleos con carga eZ _i , donde Z _i es el número atómico del i  ésimo núcleo. El observable dipolar (cantidad física) tiene el operador dipolar mecánico cuántico : ^{[ cita requerida ]}

${\displaystyle {\mathfrak {p}}=\sum _{i=1}^{N}\,q_{i}\,\mathbf {r} _{i}\,.}$

Nótese que esta definición es válida sólo para átomos o moléculas neutros, es decir, con carga total igual a cero. En el caso ionizado, tenemos

${\displaystyle {\mathfrak {p}}=\sum _{i=1}^{N}\,q_{i}\,(\mathbf {r} _{i}-\mathbf {r} _{c}),}$

donde es el centro de masa de la molécula/grupo de partículas. ^[8]${\displaystyle \mathbf {r} _{c}}$

Un átomo no degenerado ( estado S ) puede tener solo un dipolo permanente cero. Este hecho se deduce de la simetría de inversión de los átomos desde el punto de vista de la mecánica cuántica. Los tres componentes del operador dipolar son antisimétricos bajo inversión con respecto al núcleo.

${\displaystyle {\mathfrak {I}}\;{\mathfrak {p}}\;{\mathfrak {I}}^{-1}=-{\mathfrak {p}},}$

donde es el operador dipolar y es el operador de inversión.${\displaystyle {\mathfrak {p}}}$${\displaystyle {\mathfrak {I}}}$

El momento dipolar permanente de un átomo en un estado no degenerado (ver nivel de energía degenerado ) se da como el valor esperado (promedio) del operador dipolar,

${\displaystyle \left\langle {\mathfrak {p}}\right\rangle =\left\langle \,S\,|{\mathfrak {p}}|\,S\,\right\rangle ,}$

donde es una función de onda no degenerada, de estado S , que es simétrica o antisimétrica bajo inversión: . Dado que el producto de la función de onda (en el ket) y su conjugado complejo (en el bra) es siempre simétrico bajo inversión y su inversa,${\displaystyle |\,S\,\rangle }$${\displaystyle {\mathfrak {I}}\,|\,S\,\rangle =\pm |\,S\,\rangle }$

${\displaystyle \left\langle {\mathfrak {p}}\right\rangle =\left\langle \,{\mathfrak {I}}^{-1}\,S\,|{\mathfrak {p}}|\,{\mathfrak {I}}^{-1}\,S\,\right\rangle =\left\langle \,S\,|{\mathfrak {I}}\,{\mathfrak {p}}\,{\mathfrak {I}}^{-1}|\,S\,\right\rangle =-\left\langle {\mathfrak {p}}\right\rangle }$

De ello se deduce que el valor esperado cambia de signo bajo inversión. Usamos aquí el hecho de que , al ser un operador de simetría, es unitario : y por definición el adjunto hermítico puede moverse de bra a ket y luego se convierte en . Dado que la única cantidad que es igual a menos en sí es el cero, el valor esperado se desvanece,${\displaystyle {\mathfrak {I}}}$${\displaystyle {\mathfrak {I}}^{-1}={\mathfrak {I}}^{*}\,}$${\displaystyle {\mathfrak {I}}^{*}\,}$${\displaystyle {\mathfrak {I}}^{**}={\mathfrak {I}}\,}$

${\displaystyle \left\langle {\mathfrak {p}}\right\rangle =0.}$

En el caso de átomos de capa abierta con niveles de energía degenerados, se podría definir un momento dipolar con la ayuda del efecto Stark de primer orden . Esto da un dipolo no nulo (por definición proporcional a un desplazamiento de Stark de primer orden no nulo) solo si algunas de las funciones de onda que pertenecen a las energías degeneradas tienen paridad opuesta ; es decir, tienen un comportamiento diferente bajo inversión. Esto es una ocurrencia rara, pero sucede para el átomo de H excitado, donde los estados 2s y 2p son "accidentalmente" degenerados (ver el artículo Vector de Laplace–Runge–Lenz para el origen de esta degeneración) y tienen paridad opuesta (2s es par y 2p es impar).

La intensidad del campo lejano, B , de un campo magnético dipolar viene dada por

${\displaystyle B(m,r,\lambda )={\frac {\mu _{0}}{4\pi }}{\frac {m}{r^{3}}}{\sqrt {1+3\sin ^{2}(\lambda )}}\,,}$

dónde

B es la fuerza del campo, medida en teslas

r es la distancia desde el centro, medida en metros

λ es la latitud magnética (igual a 90° −  θ ) donde θ es la colatitud magnética, medida en radianes o grados desde el eje del dipolo ^{[nota 1]}

m es el momento dipolar, medido en amperios -metros cuadrados o julios por tesla

μ ₀ es la permeabilidad del espacio libre , medida en henries por metro.

La conversión a coordenadas cilíndricas se logra utilizando r ² = z ² + ρ ² y

${\displaystyle \lambda =\arcsin \left({\frac {z}{\sqrt {z^{2}+\rho ^{2}}}}\right)}$

donde ρ es la distancia perpendicular desde el eje z . Entonces,

${\displaystyle B(\rho ,z)={\frac {\mu _{0}m}{4\pi \left(z^{2}+\rho ^{2}\right)^{\frac {3}{2}}}}{\sqrt {1+{\frac {3z^{2}}{z^{2}+\rho ^{2}}}}}}$

El campo en sí es una cantidad vectorial:

${\displaystyle \mathbf {B} (\mathbf {m} ,\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\ {\frac {3(\mathbf {m} \cdot {\hat {\mathbf {r} }}){\hat {\mathbf {r} }}-\mathbf {m} }{r^{3}}}}$

dónde

B es el campo

r es el vector desde la posición del dipolo hasta la posición donde se mide el campo

r es el valor absoluto de r : la distancia desde el dipolo

r̂ = ⁠a/a⁠ es el vector unitario paralelo a r ;

m es el momento dipolar (vectorial)

μ ₀ es la permeabilidad del espacio libre

Este es exactamente el campo de un dipolo puntual, exactamente el término dipolar en la expansión multipolar de un campo arbitrario, y aproximadamente el campo de cualquier configuración tipo dipolo a grandes distancias.

El potencial vectorial A de un dipolo magnético es

${\displaystyle \mathbf {A} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {m} \times {\hat {\mathbf {r} }}}{r^{2}}}}$

con las mismas definiciones que anteriormente.

El potencial electrostático en la posición r debido a un dipolo eléctrico en el origen viene dado por:

${\displaystyle \Phi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\,{\frac {\mathbf {p} \cdot {\hat {\mathbf {r} }}}{r^{2}}}}$

donde p es el momento dipolar (vectorial) , y є ₀ es la permitividad del espacio libre .

Este término aparece como el segundo término en la expansión multipolar de un potencial electrostático arbitrario Φ( r ). Si la fuente de Φ( r ) es un dipolo, como se supone aquí, este término es el único término no nulo en la expansión multipolar de Φ( r ). El campo eléctrico de un dipolo se puede encontrar a partir del gradiente de este potencial:

${\displaystyle \mathbf {E} =-\nabla \Phi ={\frac {1}{4\pi \epsilon _{0}}}\ {\frac {3(\mathbf {p} \cdot {\hat {\mathbf {r} }}){\hat {\mathbf {r} }}-\mathbf {p} }{r^{3}}}-\delta ^{3}(\mathbf {r} ){\frac {\mathbf {p} }{3\epsilon _{0}}}.}$

Esta es la misma forma de expresión para el campo magnético de un dipolo magnético puntual, ignorando la función delta. Sin embargo, en un dipolo eléctrico real, las cargas están físicamente separadas y el campo eléctrico diverge o converge en las cargas puntuales. Esto es diferente al campo magnético de un dipolo magnético real que es continuo en todas partes. La función delta representa el campo fuerte que apunta en la dirección opuesta entre las cargas puntuales, que a menudo se omite ya que rara vez se está interesado en el campo en la posición del dipolo. Para más discusiones sobre el campo interno de los dipolos, consulte ^{[5] [9]} o Momento magnético § Campo magnético interno de un dipolo .

Dado que la dirección de un campo eléctrico se define como la dirección de la fuerza sobre una carga positiva, las líneas de campo eléctrico apuntan lejos de una carga positiva y hacia una carga negativa.

Cuando se coloca en un campo eléctrico o magnético homogéneo , surgen fuerzas iguales pero opuestas en cada lado del dipolo creando un torque τ }:

${\displaystyle {\boldsymbol {\tau }}=\mathbf {p} \times \mathbf {E} }$

para un momento dipolar eléctrico p (en culombios-metros), o

${\displaystyle {\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B} }$

para un momento dipolar magnético m (en amperios-metros cuadrados).

El par resultante tenderá a alinear el dipolo con el campo aplicado, lo que en el caso de un dipolo eléctrico, produce una energía potencial de

${\displaystyle U=-\mathbf {p} \cdot \mathbf {E} }$.

La energía de un dipolo magnético es similar

${\displaystyle U=-\mathbf {m} \cdot \mathbf {B} }$.

Además de los dipolos en electrostática, también es común considerar un dipolo eléctrico o magnético que oscila en el tiempo. Es una extensión, o un siguiente paso más físico, de la radiación de ondas esféricas .

En particular, considere un dipolo eléctrico oscilante armónicamente, con frecuencia angular ω y un momento dipolar p ₀ a lo largo de la dirección ẑ de la forma

${\displaystyle \mathbf {p} (\mathbf {r} ,t)=\mathbf {p} (\mathbf {r} )e^{-i\omega t}=p_{0}{\hat {\mathbf {z} }}e^{-i\omega t}.}$

En el vacío, el campo exacto producido por este dipolo oscilante se puede derivar utilizando la formulación de potencial retardado como:

${\displaystyle {\begin{aligned}\mathbf {E} &={\frac {1}{4\pi \varepsilon _{0}}}\left\{{\frac {\omega ^{2}}{c^{2}r}}\left({\hat {\mathbf {r} }}\times \mathbf {p} \right)\times {\hat {\mathbf {r} }}+\left({\frac {1}{r^{3}}}-{\frac {i\omega }{cr^{2}}}\right)\left(3{\hat {\mathbf {r} }}\left[{\hat {\mathbf {r} }}\cdot \mathbf {p} \right]-\mathbf {p} \right)\right\}e^{\frac {i\omega r}{c}}e^{-i\omega t}\\\mathbf {B} &={\frac {\omega ^{2}}{4\pi \varepsilon _{0}c^{3}}}({\hat {\mathbf {r} }}\times \mathbf {p} )\left(1-{\frac {c}{i\omega r}}\right){\frac {e^{i\omega r/c}}{r}}e^{-i\omega t}.\end{aligned}}}$

Para ⁠rω/do⁠  ≫ 1, el campo lejano toma la forma más simple de una onda "esférica" ​​radiante, pero con dependencia angular incorporada en el producto vectorial: ^[10]

${\displaystyle {\begin{aligned}\mathbf {B} &={\frac {\omega ^{2}}{4\pi \varepsilon _{0}c^{3}}}({\hat {\mathbf {r} }}\times \mathbf {p} ){\frac {e^{i\omega (r/c-t)}}{r}}={\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi c}}({\hat {\mathbf {r} }}\times {\hat {\mathbf {z} }}){\frac {e^{i\omega (r/c-t)}}{r}}=-{\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi c}}\sin(\theta ){\frac {e^{i\omega (r/c-t)}}{r}}\mathbf {\hat {\phi }} \\\mathbf {E} &=c\mathbf {B} \times {\hat {\mathbf {r} }}=-{\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi }}\sin(\theta )\left({\hat {\phi }}\times \mathbf {\hat {r}} \right){\frac {e^{i\omega (r/c-t)}}{r}}=-{\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi }}\sin(\theta ){\frac {e^{i\omega (r/c-t)}}{r}}{\hat {\theta }}.\end{aligned}}}$

El vector de Poynting promediado en el tiempo

${\displaystyle \langle \mathbf {S} \rangle =\left({\frac {\mu _{0}p_{0}^{2}\omega ^{4}}{32\pi ^{2}c}}\right){\frac {\sin ^{2}(\theta )}{r^{2}}}\mathbf {\hat {r}} }$

no se distribuye isótropamente, sino que se concentra en direcciones perpendiculares al momento dipolar, como resultado de las ondas eléctricas y magnéticas no esféricas. De hecho, la función armónica esférica (sen θ ) responsable de dicha distribución angular toroidal es precisamente la onda "p" l  = 1.

La potencia total promedio en el tiempo irradiada por el campo se puede derivar del vector de Poynting como

${\displaystyle P={\frac {\mu _{0}\omega ^{4}p_{0}^{2}}{12\pi c}}.}$

Obsérvese que la dependencia de la potencia de la cuarta potencia de la frecuencia de la radiación está de acuerdo con la dispersión de Rayleigh y los efectos subyacentes de por qué el cielo se compone principalmente de color azul.

Un dipolo polarizado circular se describe como una superposición de dos dipolos lineales.

• Densidad de polarización
• Modelos de dipolos magnéticos
• Modelo dipolar del campo magnético terrestre
• Electreto
• Dipolo del océano Índico y dipolo del océano Índico subtropical , dos fenómenos oceanográficos
• Interacción magnética dipolo-dipolo
• Momento magnético de giro
• Monopolo
• Armónicos sólidos
• Momentos multipolares axiales
• Momentos multipolares cilíndricos
• Momentos multipolares esféricos
• Expansión de Laplace
• Sólido molecular
• Momento magnético#Campo magnético interno de un dipolo

• Programa de geomagnetismo del USGS
• Campos de fuerza Archivado el 14 de diciembre de 2010 en Wayback Machine : un capítulo de un libro de texto en línea
• Potencial dipolar eléctrico de Stephen Wolfram y densidad de energía de un dipolo magnético de Franz Krafft. Proyecto de demostraciones de Wolfram .