Dinámica de vuelo de aeronaves

La introducción de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave . Considere ampliar la introducción para brindar una descripción general accesible de todos los aspectos importantes del artículo. ( Julio de 2018 )

La dinámica de vuelo es la ciencia que estudia la orientación y el control de los vehículos aéreos en tres dimensiones. Los tres parámetros críticos de la dinámica de vuelo son los ángulos de rotación en tres dimensiones sobre el centro de gravedad del vehículo (cg), conocidos como cabeceo , alabeo y guiñada . Estos se conocen colectivamente como actitud de la aeronave , a menudo principalmente en relación con el marco atmosférico en vuelo normal, pero también en relación con el terreno durante el despegue o el aterrizaje, o cuando se opera a baja altitud. El concepto de actitud no es específico de las aeronaves de ala fija, sino que también se extiende a las aeronaves rotatorias como los helicópteros y los dirigibles , donde la dinámica de vuelo involucrada en el establecimiento y control de la actitud es completamente diferente.

Los sistemas de control ajustan la orientación de un vehículo con respecto a su centro de gravedad. Un sistema de control incluye superficies de control que, cuando se desvían, generan un momento (o par de alerones) con respecto al centro de gravedad que hace girar la aeronave en inclinación, balanceo y guiñada. Por ejemplo, un momento de inclinación proviene de una fuerza aplicada a una distancia hacia adelante o hacia atrás del centro de gravedad, lo que hace que la aeronave incline hacia arriba o hacia abajo.

Un avión de ala fija aumenta o disminuye la sustentación generada por las alas cuando inclina el morro hacia arriba o hacia abajo aumentando o disminuyendo el ángulo de ataque (AOA). El ángulo de alabeo también se conoce como ángulo de inclinación en un avión de ala fija, que normalmente se "inclina" para cambiar la dirección horizontal del vuelo. Un avión está aerodinámico desde el morro hasta la cola para reducir la resistencia, lo que hace que sea ventajoso mantener el ángulo de deslizamiento lateral cerca de cero, aunque un avión puede "deslizarse lateralmente" deliberadamente para aumentar la resistencia y la velocidad de descenso durante el aterrizaje, para mantener el rumbo del avión igual que el rumbo de la pista durante los aterrizajes con viento cruzado y durante el vuelo con potencia asimétrica. ^[1]

El balanceo, el cabeceo y la guiñada se refieren a rotaciones sobre los respectivos ejes a partir de un estado de equilibrio de vuelo definido . El ángulo de balanceo en equilibrio se conoce como nivel de alas o ángulo de inclinación cero.

La convención aeronáutica más común define el balanceo como el que actúa sobre el eje longitudinal, positivo con el ala de estribor (derecha) abajo. La guiñada es sobre el eje vertical del cuerpo, positivo con el morro hacia estribor. El cabeceo es sobre un eje perpendicular al plano longitudinal de simetría, positivo con el morro hacia arriba. ^[2]

En la dinámica de vuelo se utilizan con frecuencia tres sistemas de coordenadas cartesianas dextrógiras . El primer sistema de coordenadas tiene un origen fijo en el marco de referencia de la Tierra:

• Marco de tierra
  • Origen: arbitrario, fijo en relación con la superficie de la Tierra.
  • Eje x _E - positivo en dirección norte
  • Eje y _E - positivo en dirección este
  • Eje z _E : positivo hacia el centro de la Tierra

En muchas aplicaciones de dinámica de vuelo, se supone que el marco de la Tierra es inercial con un plano x _E , y _E , aunque el marco de la Tierra también puede considerarse un sistema de coordenadas esféricas con origen en el centro de la Tierra.

Los otros dos marcos de referencia están fijados al cuerpo y sus orígenes se mueven junto con la aeronave, generalmente en el centro de gravedad. Para una aeronave que es simétrica de derecha a izquierda, los marcos se pueden definir como:

• Marco de la carrocería
  • Origen - centro de gravedad del avión
  • Eje x _b - positivo que sale del morro del avión en el plano de simetría del avión
  • Eje z _b : perpendicular al eje x _b , en el plano de simetría de la aeronave, positivo debajo de la aeronave
  • Eje yb : _{perpendicular} al plano xb , zb , positivo determinado por la _regla de la mano derecha ( _generalmente , positivo en el ala derecha)
• Marco de viento
  • Origen - centro de gravedad del avión
  • Eje x _w : positivo en la dirección del vector de velocidad de la aeronave con respecto al aire.
  • Eje z _w : perpendicular al eje x _w , en el plano de simetría de la aeronave, positivo debajo de la aeronave.
  • _{Eje yw} : perpendicular al plano xw , zw _, positivo determinado por la regla de la mano derecha (generalmente, positivo hacia la derecha ₎

Los aviones asimétricos tienen marcos fijos de carrocería análogos, pero se deben utilizar convenciones diferentes para elegir las direcciones precisas de los ejes x y z .

El marco de referencia terrestre es un marco conveniente para expresar la cinemática de traslación y rotación de la aeronave. El marco de referencia terrestre también es útil porque, bajo ciertas suposiciones, se puede aproximar como inercial. Además, una fuerza que actúa sobre la aeronave, el peso, está fija en la dirección + z _E.

El marco de la carrocería suele ser de interés porque el origen y los ejes permanecen fijos en relación con la aeronave. Esto significa que la orientación relativa de la Tierra y los marcos de la carrocería describe la actitud de la aeronave. Además, la dirección de la fuerza de empuje generalmente está fija en el marco de la carrocería, aunque algunas aeronaves pueden variar esta dirección, por ejemplo, mediante la vectorización del empuje .

El marco de viento es un marco conveniente para expresar las fuerzas y momentos aerodinámicos que actúan sobre una aeronave. En particular, la fuerza aerodinámica neta se puede dividir en componentes a lo largo de los ejes del marco de viento, con la _fuerza de arrastre en la dirección -xw y la fuerza de sustentación en la _dirección -zw .

Además de definir los marcos de referencia, se puede determinar la orientación relativa de los mismos. La orientación relativa se puede expresar de diversas formas, entre ellas:

• Matrices de rotación
• Cosenos de dirección
• Ángulos de Euler
• Cuaterniones

Los diversos ángulos de Euler que relacionan los tres marcos de referencia son importantes para la dinámica del vuelo. Existen muchas convenciones de ángulos de Euler, pero todas las secuencias de rotación que se presentan a continuación utilizan la convención zy'-x" . Esta convención corresponde a un tipo de ángulos de Tait-Bryan , que se conocen comúnmente como ángulos de Euler. Esta convención se describe en detalle a continuación para los ángulos de Euler de balanceo, cabeceo y guiñada que describen la orientación del marco del cuerpo en relación con el marco de la Tierra. Los otros conjuntos de ángulos de Euler se describen a continuación por analogía.

• En primer lugar, giramos los ejes x _E e y E _del marco de referencia terrestre alrededor del eje z _E en el ángulo de guiñada ψ . Esto da como resultado un marco de referencia intermedio con ejes denominados x ' ,y ' ,z ' , donde z'=z _E .
• En segundo lugar, giramos los ejes x ' y z ' alrededor del eje y ' en el ángulo de inclinación θ . Esto da como resultado otro marco de referencia intermedio con ejes denominados x",y",z" , donde y"=y ' .
• Por último, giramos los ejes y" y z" alrededor del eje x" en el ángulo de giro φ . El marco de referencia que resulta después de las tres rotaciones es el marco de la carrocería.

Basado en las convenciones de rotaciones y ejes anteriores:

• Ángulo de guiñada ψ: ángulo entre el norte y la proyección del eje longitudinal de la aeronave sobre el plano horizontal;
• Ángulo de cabeceo θ: ángulo entre el eje longitudinal de la aeronave y la horizontal;
• Ángulo de alabeo φ: rotación alrededor del eje longitudinal de la aeronave después de girar en guiñada y cabeceo.

• Ángulo de rumbo σ: ángulo entre el componente norte y el horizontal del vector de velocidad, que describe en qué dirección se mueve la aeronave en relación con las direcciones cardinales.
• Ángulo de trayectoria de vuelo γ: es el ángulo entre la horizontal y el vector de velocidad, que describe si la aeronave está subiendo o descendiendo.
• Ángulo de inclinación μ: representa una rotación de la fuerza de sustentación alrededor del vector de velocidad, que puede indicar si el avión está girando .

Al realizar las rotaciones descritas anteriormente para obtener el marco del cuerpo a partir del marco de la Tierra, existe esta analogía entre los ángulos:

• σ, ψ (rumbo vs. guiñada)
• γ, θ (trayectoria de vuelo vs. inclinación)
• μ, φ (Banco vs Roll)

• ángulo de deslizamiento lateral β: ángulo entre el vector de velocidad y la proyección del eje longitudinal de la aeronave sobre el plano x _w ,y _w , que describe si hay un componente lateral en la velocidad de la aeronave

• ángulo de ataque α : ángulo entre el plano x _w , y _w y el eje longitudinal de la aeronave y, entre otras cosas, es una variable importante para determinar la magnitud de la fuerza de sustentación

Al realizar las rotaciones descritas anteriormente para obtener el marco del cuerpo a partir del marco de la Tierra, existe esta analogía entre los ángulos:

• β, ψ (deslizamiento lateral vs. guiñada)
• α , θ (ataque vs tono)
• (φ = 0) (nada vs rodar)

Entre los tres marcos de referencia existen pues estas analogías:

• Guiñada / Rumbo / Deslizamiento lateral (eje Z, vertical)
• Inclinación / Trayectoria de vuelo / Ángulo de ataque (eje Y, ala)
• Balanceo/Inclinación/nada (eje X, morro)

Al analizar la estabilidad de una aeronave, es habitual considerar perturbaciones en relación con un estado de vuelo estable nominal . Por lo tanto, el análisis se aplicaría, por ejemplo, suponiendo que:

Vuelo recto y nivelado

Girar a velocidad constante

Aproximación y aterrizaje

Despegar

La velocidad, la altura y el ángulo de ataque son diferentes para cada condición de vuelo, además, la aeronave estará configurada de manera diferente, por ejemplo, a baja velocidad los flaps pueden estar desplegados y el tren de aterrizaje puede estar abajo.

A excepción de los diseños asimétricos (o diseños simétricos con deslizamiento lateral significativo), las ecuaciones de movimiento longitudinal (que involucran fuerzas de inclinación y sustentación) pueden tratarse independientemente del movimiento lateral (que involucra balanceo y guiñada).

A continuación se consideran perturbaciones sobre una trayectoria de vuelo nominal recta y nivelada.

Para que el análisis sea relativamente simple, se supone que las superficies de control están fijas durante todo el movimiento, lo que se conoce como estabilidad fija. El análisis sin estabilidad requiere la complicación adicional de tener en cuenta el movimiento de las superficies de control.

Además, se supone que el vuelo se realiza en aire en calma y el avión se trata como un cuerpo rígido .

Sobre un avión en vuelo actúan tres fuerzas: el peso , el empuje y la fuerza aerodinámica .

La expresión para calcular la fuerza aerodinámica es:

${\displaystyle \mathbf {F} _{A}=\int _{\Sigma }(-\Delta p\mathbf {n} +\mathbf {f} )\,d\sigma }$

dónde:

${\displaystyle \Delta p\equiv}$Diferencia entre presión estática y presión de corriente libre

${\displaystyle \mathbf {n} \equiv}$vector normal exterior del elemento de área

${\displaystyle \mathbf {f} \equiv}$vector de tensión tangencial ejercido por el aire sobre el cuerpo

${\displaystyle \Sigma \equiv }$superficie de referencia adecuada

Proyectado sobre los ejes del viento obtenemos:

${\displaystyle \mathbf {F} _{A}=-(\mathbf {i} _{w}D+\mathbf {j} _{w}Q+\mathbf {k} _{w}L)}$

dónde:

${\displaystyle D\equiv }$Arrastrar

${\displaystyle Q\equiv }$Fuerza lateral

${\displaystyle L\equiv }$Elevar

Presión dinámica de la corriente libre${\displaystyle \equiv q={\tfrac {1}{2}}\,\rho \,V^{2}}$

Superficie de referencia adecuada ( superficie del ala , en el caso de aviones )${\displaystyle \equiv S}$

Coeficiente de presión ${\displaystyle \equiv C_{p}={\dfrac {p-p_{\infty }}{q}}}$

Coeficiente de fricción ${\displaystyle \equiv C_{f}={\dfrac {f}{q}}}$

Coeficiente de arrastre ${\displaystyle \equiv C_{d}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {i_{w}} +C_{f}\mathbf {t} \bullet \mathbf {i_{w}} ]\,d\sigma }$

Coeficiente de fuerza lateral${\displaystyle \equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma }$

Coeficiente de sustentación ${\displaystyle \equiv C_{L}={\dfrac {L}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {k_{w}} +C_{f}\mathbf {t} \bullet \mathbf {k_{w}} ]\,d\sigma }$

Es necesario conocer C _p y C _f en cada punto de la superficie considerada.

En ausencia de efectos térmicos, hay tres números adimensionales notables:

• Compresibilidad del flujo:

Número de Mach ${\displaystyle \equiv M={\dfrac {V}{a}}}$

• Viscosidad del flujo:

Número de Reynolds ${\displaystyle \equiv Re={\dfrac {\rho Vl}{\mu }}}$

• Rarefacción del flujo:

Número de Knudsen ${\displaystyle \equiv Kn={\dfrac {\lambda }{l}}}$

dónde:

${\displaystyle a={\sqrt {kR\theta }}\equiv }$velocidad del sonido

${\displaystyle k\equiv }$ relación de calor específico

${\displaystyle R\equiv }$ constante de gas por unidad de masa

${\displaystyle \theta \equiv }$temperatura absoluta

${\displaystyle \lambda ={\dfrac {\mu }{\rho }}{\sqrt {\dfrac {\pi }{2R\theta }}}={\dfrac {M}{Re}}{\sqrt {\dfrac {k\pi }{2}}}\equiv }$ camino libre medio

Según λ existen tres posibles grados de rarefacción y sus movimientos correspondientes se denominan:

• Corriente continua (rarefacción despreciable):${\displaystyle {\dfrac {M}{Re}}\ll 1}$
• Corriente de transición (rarefacción moderada):${\displaystyle {\dfrac {M}{Re}}\approx 1}$
• Corriente molecular libre (alta rarefacción):${\displaystyle {\dfrac {M}{Re}}\gg 1}$

El movimiento de un cuerpo a través de una corriente se considera, en dinámica de vuelo, como una corriente continua. En la capa exterior del espacio que rodea al cuerpo, la viscosidad será despreciable. Sin embargo, los efectos de la viscosidad deberán tenerse en cuenta al analizar el flujo en las proximidades de la capa límite .

Dependiendo de la compresibilidad del flujo, se pueden considerar diferentes tipos de corrientes:

• Corriente subsónica incompresible :${\displaystyle 0<M<0.3}$
• Corriente subsónica compresible :${\displaystyle 0.3<M<0.8}$
• Corriente transónica :${\displaystyle 0.8<M<1.2}$
• Corriente supersónica :${\displaystyle 1.2<M<5}$
• Corriente hipersónica :${\displaystyle 5<M}$

Si la geometría del cuerpo es fija y en caso de vuelo simétrico (β=0 y Q=0), los coeficientes de presión y fricción son funciones que dependen de:

${\displaystyle C_{p}=C_{p}(\alpha ,M,Re,P)}$

${\displaystyle C_{f}=C_{f}(\alpha ,M,Re,P)}$

dónde:

${\displaystyle \alpha \equiv }$ ángulo de ataque

${\displaystyle P\equiv }$punto considerado de la superficie

En estas condiciones, los coeficientes de resistencia y sustentación son funciones que dependen exclusivamente del ángulo de ataque del fuselaje y de los números de Mach y Reynolds . La eficiencia aerodinámica, definida como la relación entre los coeficientes de sustentación y de resistencia, también dependerá de estos parámetros.

${\displaystyle {\begin{cases}C_{D}=C_{D}(\alpha ,M,Re)\\C_{L}=C_{L}(\alpha ,M,Re)\\E=E(\alpha ,M,Re)={\dfrac {C_{L}}{C_{D}}}\\\end{cases}}}$

También es posible obtener la dependencia del coeficiente de arrastre respecto del coeficiente de sustentación . Esta relación se conoce como ecuación del coeficiente de arrastre:

${\displaystyle C_{D}=C_{D}(C_{L},M,Re)\equiv }$ecuación del coeficiente de arrastre

La eficiencia aerodinámica tiene un valor máximo, E _max , con respecto a C _L donde la línea tangente desde el origen de coordenadas toca el gráfico de la ecuación del coeficiente de arrastre.

El coeficiente de arrastre, C _D , se puede descomponer de dos maneras. La primera descomposición típica separa los efectos de la presión y la fricción:

${\displaystyle C_{D}=C_{Df}+C_{Dp}{\begin{cases}C_{Df}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }C_{f}\mathbf {t} \bullet \mathbf {i_{w}} \,d\sigma \\C_{Dp}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }(-C_{p})\mathbf {n} \bullet \mathbf {i_{w}} \,d\sigma \end{cases}}}$

Existe una segunda descomposición típica que tiene en cuenta la definición de la ecuación del coeficiente de arrastre. Esta descomposición separa el efecto del coeficiente de sustentación en la ecuación, obteniendo dos términos C _D0 y C _Di . C _D0 se conoce como el coeficiente de arrastre parásito y es el coeficiente de arrastre base en sustentación cero. C _Di se conoce como el coeficiente de arrastre inducido y es producido por la sustentación de la carrocería.

${\displaystyle C_{D}=C_{D0}+C_{Di}{\begin{cases}C_{D0}=(C_{D})_{C_{L}=0}\\C_{Di}\end{cases}}}$

Un buen intento para el coeficiente de arrastre inducido es suponer una dependencia parabólica de la sustentación.

${\displaystyle C_{Di}=kC_{L}^{2}\Rightarrow C_{D}=C_{D0}+kC_{L}^{2}}$

La eficiencia aerodinámica ahora se calcula como:

${\displaystyle E={\dfrac {C_{L}}{C_{D0}+kC_{L}^{2}}}\Rightarrow {\begin{cases}E_{max}={\dfrac {1}{2{\sqrt {kC_{D0}}}}}\\(C_{L})_{Emax}={\sqrt {\dfrac {C_{D0}}{k}}}\\(C_{Di})_{Emax}=C_{D0}\end{cases}}}$

Si la configuración del avión es simétrica respecto al plano XY, el coeficiente de arrastre mínimo es igual al arrastre parásito del avión.

${\displaystyle C_{Dmin}=(C_{D})_{CL=0}=C_{D0}}$

Sin embargo, en caso de que la configuración sea asimétrica respecto del plano XY, la resistencia mínima difiere de la resistencia parásita. En estos casos, se puede trazar una nueva ecuación aproximada de resistencia parabólica que deje el valor mínimo de resistencia en un valor de sustentación cero.

${\displaystyle C_{Dmin}=C_{DM}\neq (C_{D})_{CL=0}}$

${\displaystyle C_{D}=C_{DM}+k(C_{L}-C_{LM})^{2}}$

El coeficiente de presión varía con el número de Mach según la relación que se indica a continuación: ^[4]

${\displaystyle C_{p}={\frac {C_{p0}}{\sqrt {|1-{M_{\infty }}^{2}|}}}}$

dónde

• C _p es el coeficiente de presión compresible
• C _p0 es el coeficiente de presión incompresible
• M _∞ es el número de Mach de corriente libre.

Esta relación es razonablemente precisa para 0,3 < M < 0,7 y cuando M = 1 se convierte en ∞, lo cual es una situación física imposible y se denomina singularidad de Prandtl-Glauert .

ver Fuerza aerodinámica

La estabilidad es la capacidad de la aeronave para contrarrestar las perturbaciones en su trayectoria de vuelo.

Según David P. Davies , existen seis tipos de estabilidad de una aeronave: estabilidad de velocidad, estabilidad longitudinal estática sin palanca, estabilidad lateral estática, estabilidad direccional, estabilidad oscilatoria y estabilidad en espiral. ^{[5] : 164}

Un avión en vuelo de crucero suele tener una velocidad estable. Si la velocidad aumenta, la resistencia aumenta, lo que reducirá la velocidad hasta el equilibrio para su configuración y ajuste de empuje. Si la velocidad disminuye, la resistencia disminuye y el avión acelerará hasta alcanzar su velocidad de equilibrio, donde el empuje es igual a la resistencia.

Sin embargo, en vuelo lento, debido a la resistencia inducida por la sustentación , a medida que disminuye la velocidad, la resistencia aumenta (y viceversa). Esto se conoce como la "parte posterior de la curva de resistencia ". La aeronave será inestable en cuanto a velocidad, porque una disminución de la velocidad provocará una disminución adicional de la velocidad.

La estabilidad longitudinal se refiere a la estabilidad de una aeronave en el cabeceo. En el caso de una aeronave estable, si la aeronave se inclina hacia arriba, las alas y la cola crean un momento de inclinación hacia abajo que tiende a restaurar la aeronave a su actitud original. En el caso de una aeronave inestable, una alteración en el cabeceo dará lugar a un momento de cabeceo cada vez mayor. La estabilidad estática longitudinal es la capacidad de una aeronave de recuperarse de una alteración inicial. La estabilidad dinámica longitudinal se refiere a la amortiguación de estos momentos estabilizadores, lo que evita oscilaciones persistentes o crecientes en el cabeceo.

La estabilidad direccional o de veleta se refiere a la estabilidad estática del avión respecto del eje z. Al igual que en el caso de la estabilidad longitudinal, es deseable que el avión tienda a volver a una condición de equilibrio cuando se somete a algún tipo de perturbación de guiñada. Para ello, la pendiente de la curva del momento de guiñada debe ser positiva. Un avión que posee este modo de estabilidad siempre apuntará hacia el viento relativo, de ahí el nombre de estabilidad de veleta.

It has been suggested that this section be moved into Aircraft dynamic modes. (Discuss) (April 2024)

Es una práctica común derivar una ecuación característica de cuarto orden para describir el movimiento longitudinal y luego factorizarla aproximadamente en un modo de alta frecuencia y un modo de baja frecuencia. El enfoque adoptado aquí consiste en utilizar el conocimiento cualitativo del comportamiento de las aeronaves para simplificar las ecuaciones desde el principio y llegar al resultado por una vía más accesible.

Los dos movimientos longitudinales (modos) se denominan oscilación de paso de período corto (SPPO) y fugoide .

Una entrada breve (en la terminología de los sistemas de control , un impulso ) en el cabeceo (generalmente a través del elevador en una aeronave de ala fija con configuración estándar) generalmente provocará sobrepasos con respecto a la condición de compensación. La transición se caracteriza por un movimiento armónico simple amortiguado con respecto a la nueva compensación. Hay muy pocos cambios en la trayectoria durante el tiempo que tarda la oscilación en amortiguarse.

Generalmente, esta oscilación es de alta frecuencia (por lo tanto, de período corto) y se amortigua durante un período de unos pocos segundos. Un ejemplo del mundo real implicaría que un piloto seleccione una nueva actitud de ascenso, por ejemplo, 5° de morro hacia arriba desde la actitud original. Se puede utilizar un tirón corto y brusco hacia atrás en la columna de control, y generalmente conducirá a oscilaciones sobre la nueva condición de compensación. Si las oscilaciones están mal amortiguadas, la aeronave tardará un largo período de tiempo en asentarse en la nueva condición, lo que puede conducir a una oscilación inducida por el piloto . Si el modo de período corto es inestable, generalmente será imposible para el piloto controlar la aeronave de manera segura durante cualquier período de tiempo.

Este movimiento armónico amortiguado se denomina oscilación de cabeceo de período corto ; surge de la tendencia de una aeronave estable a apuntar en la dirección general de vuelo. Es muy similar en naturaleza al modo veleta de las configuraciones de misiles o cohetes. El movimiento involucra principalmente la actitud de cabeceo (theta) y la incidencia (alfa). La dirección del vector de velocidad, relativa a los ejes inerciales es . El vector de velocidad es: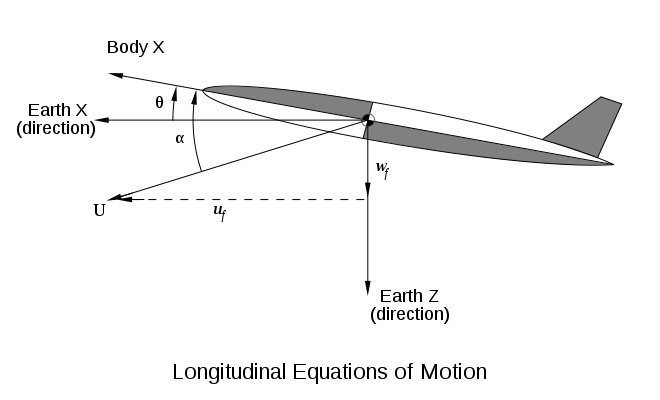${\displaystyle \theta }$${\displaystyle \alpha }$${\displaystyle \theta -\alpha }$

${\displaystyle u_{f}=U\cos(\theta -\alpha )}$

No se pudo analizar (SVG (MathML se puede habilitar a través del complemento del navegador): Respuesta no válida ("La extensión Math no se puede conectar a Restbase") del servidor "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle w_f=U\sin(\theta-\alpha)}

donde , son los componentes de la velocidad en los ejes inerciales. Según la segunda ley de Newton , las aceleraciones son proporcionales a las fuerzas , por lo que las fuerzas en los ejes inerciales son:${\displaystyle u_{f}}$${\displaystyle w_{f}}$

${\displaystyle X_{f}=m{\frac {du_{f}}{dt}}=m{\frac {dU}{dt}}\cos(\theta -\alpha )-mU{\frac {d(\theta -\alpha )}{dt}}\sin(\theta -\alpha )}$

${\displaystyle Z_{f}=m{\frac {dw_{f}}{dt}}=m{\frac {dU}{dt}}\sin(\theta -\alpha )+mU{\frac {d(\theta -\alpha )}{dt}}\cos(\theta -\alpha )}$

donde m es la masa . Por la naturaleza del movimiento, la variación de velocidad es despreciable durante el período de oscilación, por lo que:${\displaystyle m{\frac {dU}{dt}}}$

${\displaystyle X_{f}=-mU{\frac {d(\theta -\alpha )}{dt}}\sin(\theta -\alpha )}$

${\displaystyle Z_{f}=mU{\frac {d(\theta -\alpha )}{dt}}\cos(\theta -\alpha )}$

Pero las fuerzas se generan por la distribución de la presión sobre el cuerpo y se refieren al vector de velocidad. Pero el conjunto de ejes de velocidad (viento) no es un sistema inercial , por lo que debemos resolver las fuerzas de los ejes fijos en ejes de viento. Además, solo nos interesa la fuerza a lo largo del eje z:

${\displaystyle Z=-Z_{f}\cos(\theta -\alpha )+X_{f}\sin(\theta -\alpha )}$

O:

${\displaystyle Z=-mU{\frac {d(\theta -\alpha )}{dt}}}$

En palabras, la fuerza del eje del viento es igual a la aceleración centrípeta .

La ecuación del momento es la derivada temporal del momento angular :

${\displaystyle M=B{\frac {d^{2}\theta }{dt^{2}}}}$

donde M es el momento de cabeceo y B es el momento de inercia respecto del eje de cabeceo. Sea: , la velocidad de cabeceo. Las ecuaciones de movimiento, con todas las fuerzas y momentos referidos a los ejes del viento son, por lo tanto:${\displaystyle {\frac {d\theta }{dt}}=q}$

${\displaystyle {\frac {d\alpha }{dt}}=q+{\frac {Z}{mU}}}$

${\displaystyle {\frac {dq}{dt}}={\frac {M}{B}}}$

Nos ocupamos únicamente de las perturbaciones en fuerzas y momentos, debidas a perturbaciones en los estados y q, y sus derivadas temporales. Estas se caracterizan por las derivadas de estabilidad determinadas a partir de la condición de vuelo. Las posibles derivadas de estabilidad son:${\displaystyle \alpha }$

${\displaystyle Z_{\alpha }}$Elevación debida a la incidencia, esta es negativa porque el eje z está hacia abajo mientras que la incidencia positiva provoca una fuerza hacia arriba.

${\displaystyle Z_{q}}$La sustentación debida a la velocidad de cabeceo surge del aumento de la incidencia de la cola, por lo tanto también es negativa, pero pequeña en comparación con .${\displaystyle Z_{\alpha }}$

${\displaystyle M_{\alpha }}$ Momento de cabeceo debido a la incidencia: término de estabilidad estática. La estabilidad estática requiere que este sea negativo.

${\displaystyle M_{q}}$ Momento de cabeceo debido a la velocidad de cabeceo: término de amortiguación del cabeceo, que siempre es negativo.

Dado que la cola está operando en el campo de flujo del ala, los cambios en la incidencia del ala provocan cambios en la corriente descendente, pero hay un retraso para que el cambio en el campo de flujo del ala afecte la elevación de la cola, esto se representa como un momento proporcional a la tasa de cambio de incidencia:

${\displaystyle M_{\dot {\alpha }}}$

El efecto de caída retardada le da a la cola más sustentación y produce un momento de morro hacia abajo, por lo que se espera que sea negativo.${\displaystyle M_{\dot {\alpha }}}$

Las ecuaciones de movimiento, con pequeñas fuerzas de perturbación y momentos, se convierten en:

${\displaystyle {\frac {d\alpha }{dt}}=\left(1+{\frac {Z_{q}}{mU}}\right)q+{\frac {Z_{\alpha }}{mU}}\alpha }$

${\displaystyle {\frac {dq}{dt}}={\frac {M_{q}}{B}}q+{\frac {M_{\alpha }}{B}}\alpha +{\frac {M_{\dot {\alpha }}}{B}}{\dot {\alpha }}}$

Estos pueden manipularse para producir una ecuación diferencial lineal de segundo orden en :${\displaystyle \alpha }$

${\displaystyle {\frac {d^{2}\alpha }{dt^{2}}}-\left({\frac {Z_{\alpha }}{mU}}+{\frac {M_{q}}{B}}+(1+{\frac {Z_{q}}{mU}}){\frac {M_{\dot {\alpha }}}{B}}\right){\frac {d\alpha }{dt}}+\left({\frac {Z_{\alpha }}{mU}}{\frac {M_{q}}{B}}-{\frac {M_{\alpha }}{B}}(1+{\frac {Z_{q}}{mU}})\right)\alpha =0}$

Esto representa un movimiento armónico simple amortiguado.

Debemos esperar que sea pequeño en comparación con la unidad, por lo que el coeficiente de (el término 'rigidez') será positivo, siempre que . Esta expresión está dominada por , que define la estabilidad estática longitudinal de la aeronave, debe ser negativa para la estabilidad. El término de amortiguamiento se reduce por el efecto de la corriente descendente, y es difícil diseñar una aeronave con una respuesta natural rápida y una amortiguación intensa. Por lo general, la respuesta está subamortiguada pero es estable.${\displaystyle {\frac {Z_{q}}{mU}}}$${\displaystyle \alpha }$${\displaystyle M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}}$${\displaystyle M_{\alpha }}$

Si se mantiene la palanca fija, el avión no mantendrá un vuelo recto y nivelado (excepto en el improbable caso de que esté perfectamente ajustado para un vuelo nivelado con su altitud y potencia actuales), sino que comenzará a descender, nivelarse y ascender nuevamente. Repetirá este ciclo hasta que intervenga el piloto. Esta oscilación de largo período en velocidad y altura se denomina modo fugoide . Se analiza suponiendo que el SSPO realiza su función adecuada y mantiene el ángulo de ataque cerca de su valor nominal. Los dos estados que se ven afectados principalmente son el ángulo de trayectoria de vuelo (gamma) y la velocidad. Las ecuaciones de movimiento de pequeña perturbación son:${\displaystyle \gamma }$

${\displaystyle mU{\frac {d\gamma }{dt}}=-Z}$

lo que significa que la fuerza centrípeta es igual a la perturbación en la fuerza de sustentación.

Para la velocidad, resolviendo a lo largo de la trayectoria:

${\displaystyle m{\frac {du}{dt}}=X-mg\gamma }$

donde g es la aceleración debida a la gravedad en la superficie de la Tierra . La aceleración a lo largo de la trayectoria es igual a la fuerza neta en sentido x menos el componente de peso. No debemos esperar que las derivadas aerodinámicas significativas dependan del ángulo de la trayectoria de vuelo, por lo que solo se deben considerar y . es el incremento de la resistencia con el aumento de la velocidad, es negativo, de la misma manera es el incremento de la sustentación debido al incremento de la velocidad, también es negativo porque la sustentación actúa en sentido opuesto al eje z.${\displaystyle X_{u}}$${\displaystyle Z_{u}}$${\displaystyle X_{u}}$${\displaystyle Z_{u}}$

Las ecuaciones de movimiento se convierten en:

${\displaystyle mU{\frac {d\gamma }{dt}}=-Z_{u}u}$

${\displaystyle m{\frac {du}{dt}}=X_{u}u-mg\gamma }$

Estos pueden expresarse como una ecuación de segundo orden en el ángulo de la trayectoria de vuelo o la perturbación de la velocidad:

${\displaystyle {\frac {d^{2}u}{dt^{2}}}-{\frac {X_{u}}{m}}{\frac {du}{dt}}-{\frac {Z_{u}g}{mU}}u=0}$

Ahora la sustentación es casi igual al peso:

${\displaystyle Z={\frac {1}{2}}\rho U^{2}c_{L}S_{w}=W}$

donde es la densidad del aire, es el área del ala, W el peso y es el coeficiente de sustentación (se supone constante porque la incidencia es constante), tenemos, aproximadamente:${\displaystyle \rho }$${\displaystyle S_{w}}$${\displaystyle c_{L}}$

${\displaystyle Z_{u}={\frac {2W}{U}}={\frac {2mg}{U}}}$

El período del fugoide, T, se obtiene a partir del coeficiente de u:

${\displaystyle {\frac {2\pi }{T}}={\sqrt {\frac {2g^{2}}{U^{2}}}}}$

O:

${\displaystyle T={\frac {2\pi U}{{\sqrt {2}}g}}}$

Como la sustentación es mucho mayor que la resistencia, el fugoide, en el mejor de los casos, se amortigua ligeramente. Una hélice con velocidad fija sería de ayuda. Una fuerte amortiguación de la rotación del paso o una gran inercia rotacional aumentan el acoplamiento entre los modos de período corto y fugoide, de modo que estos modificarán el fugoide.

En un cohete o misil simétrico, la estabilidad direccional en guiñada es la misma que la estabilidad de cabeceo; se asemeja a la oscilación de cabeceo de período corto, con equivalentes en el plano de guiñada a las derivadas de estabilidad del plano de cabeceo. Por esta razón, la estabilidad direccional de cabeceo y guiñada se conocen colectivamente como la estabilidad de "veleta" del misil.

Las aeronaves carecen de simetría entre el cabeceo y la guiñada, por lo que la estabilidad direccional en la guiñada se deriva de un conjunto diferente de derivadas de estabilidad. El plano de guiñada equivalente a la oscilación de cabeceo de período corto, que describe la estabilidad direccional del plano de guiñada, se denomina balanceo holandés. A diferencia de los movimientos del plano de cabeceo, los modos laterales implican tanto el movimiento de balanceo como el de guiñada.

Es habitual derivar las ecuaciones de movimiento mediante manipulación formal, lo que, para el ingeniero, equivale a un juego de manos matemático. El enfoque actual sigue el análisis del plano de inclinación al formular las ecuaciones en términos de conceptos que son razonablemente familiares.

La aplicación de un impulso a través de los pedales del timón debería inducir un balanceo holandés , que es la oscilación entre el balanceo y la guiñada, con el movimiento de balanceo rezagado respecto del guiñada en un cuarto de ciclo, de modo que las puntas de las alas sigan trayectorias elípticas con respecto al avión.

La ecuación de traslación del plano de guiñada, al igual que en el plano de cabeceo, iguala la aceleración centrípeta a la fuerza lateral.

${\displaystyle {\frac {d\beta }{dt}}={\frac {Y}{mU}}-r}$

donde (beta) es el ángulo de deslizamiento lateral , Y la fuerza lateral y r la velocidad de guiñada.${\displaystyle \beta }$

Las ecuaciones de momento son un poco más complicadas. La condición de equilibrio se da cuando la aeronave se encuentra en un ángulo de ataque con respecto al flujo de aire. El eje x del cuerpo no se alinea con el vector de velocidad, que es la dirección de referencia para los ejes del viento. En otras palabras, los ejes del viento no son ejes principales (la masa no se distribuye simétricamente sobre los ejes de guiñada y alabeo). Consideremos el movimiento de un elemento de masa en la posición -z, x en la dirección del eje y, es decir, hacia el plano del papel.

Si la velocidad de giro es p, la velocidad de la partícula es:

${\displaystyle v=-pz+xr}$

Compuesta por dos términos, la fuerza sobre esta partícula es, en primer lugar, proporcional a la velocidad de cambio de v, y en segundo lugar, se debe al cambio de dirección de este componente de la velocidad a medida que el cuerpo se mueve. Los últimos términos dan lugar a productos vectoriales de pequeñas cantidades (pq, pr, qr), que luego se descartan. En este análisis, se descartan desde el principio para mayor claridad. En efecto, suponemos que la dirección de la velocidad de la partícula debida a las velocidades simultáneas de balanceo y guiñada no cambia significativamente a lo largo del movimiento. Con esta suposición simplificadora, la aceleración de la partícula se convierte en:

${\displaystyle {\frac {dv}{dt}}=-{\frac {dp}{dt}}z+{\frac {dr}{dt}}x}$

El momento de guiñada viene dado por:

${\displaystyle \delta mx{\frac {dv}{dt}}=-{\frac {dp}{dt}}xz\delta m+{\frac {dr}{dt}}x^{2}\delta m}$

Hay un momento de guiñada adicional debido al desplazamiento de la partícula en la dirección y:${\displaystyle {\frac {dr}{dt}}y^{2}\delta m}$

El momento de guiñada se obtiene sumando todas las partículas del cuerpo:

${\displaystyle N=-{\frac {dp}{dt}}\int xzdm+{\frac {dr}{dt}}\int x^{2}+y^{2}dm=-E{\frac {dp}{dt}}+C{\frac {dr}{dt}}}$

donde N es el momento de guiñada, E es un producto de inercia y C es el momento de inercia sobre el eje de guiñada . Un razonamiento similar da como resultado la ecuación de balanceo:

${\displaystyle L=A{\frac {dp}{dt}}-E{\frac {dr}{dt}}}$

donde L es el momento de rodadura y A el momento de inercia de rodadura.

Los estados son (deslizamiento lateral), r (velocidad de guiñada) y p (velocidad de alabeo), con momentos N (guiñada) y L (alabeo), y fuerza Y (desplazamiento lateral). Hay nueve derivadas de estabilidad relevantes para este movimiento; a continuación se explica cómo se originan. Sin embargo, se puede obtener una mejor comprensión intuitiva simplemente jugando con un modelo de avión y considerando cómo las fuerzas sobre cada componente se ven afectadas por los cambios en el deslizamiento lateral y la velocidad angular: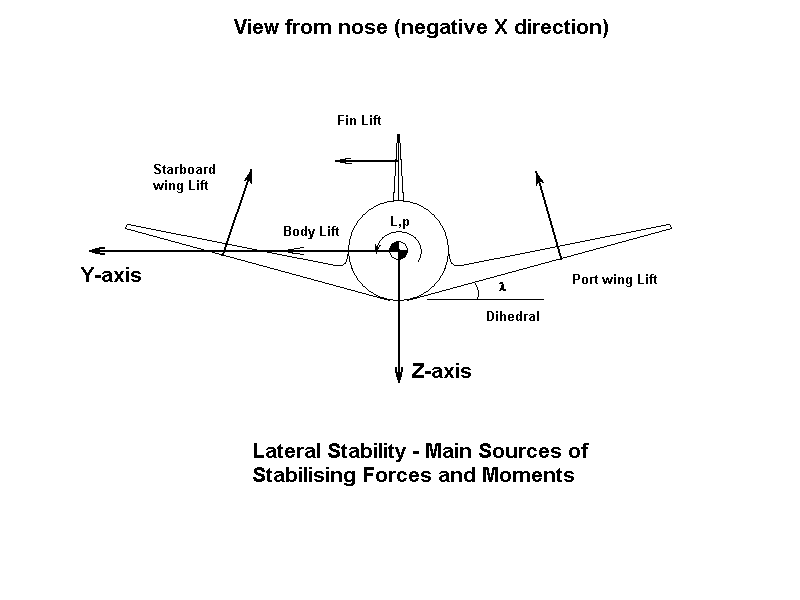${\displaystyle \beta }$

${\displaystyle Y_{\beta }}$Fuerza lateral debido al deslizamiento lateral (en ausencia de guiñada).

El deslizamiento lateral genera una fuerza lateral desde la aleta y el fuselaje. Además, si el ala tiene diedro, el deslizamiento lateral en un ángulo de alabeo positivo aumenta la incidencia en el ala de estribor y la reduce en el lado de babor, lo que resulta en un componente de fuerza neta directamente opuesto a la dirección del deslizamiento lateral. El barrido hacia atrás de las alas tiene el mismo efecto en la incidencia, pero como las alas no están inclinadas en el plano vertical, el barrido hacia atrás por sí solo no afecta . Sin embargo, se puede utilizar anhedral con ángulos de barrido hacia atrás altos en aeronaves de alto rendimiento para compensar los efectos de incidencia del ala del deslizamiento lateral. Curiosamente, esto no invierte el signo de la contribución de la configuración del ala a (en comparación con el caso diedro).${\displaystyle Y_{\beta }}$${\displaystyle Y_{\beta }}$

${\displaystyle Y_{p}}$Fuerza lateral debido a la velocidad de balanceo.

La velocidad de alabeo provoca una incidencia en la aleta, que genera una fuerza lateral correspondiente. Además, el alabeo positivo (ala de estribor hacia abajo) aumenta la sustentación en el ala de estribor y la reduce en el ala de babor. Si el ala tiene diedro, esto dará como resultado una fuerza lateral que se opondrá momentáneamente a la tendencia resultante de deslizamiento lateral. Las configuraciones de ala anédrica y/o estabilizador pueden hacer que el signo de la fuerza lateral se invierta si se anula el efecto de la aleta.

${\displaystyle Y_{r}}$Fuerza lateral debido a la velocidad de guiñada.

La guiñada genera fuerzas laterales debido a la incidencia en el timón, la aleta y el fuselaje.

${\displaystyle N_{\beta }}$Momento de guiñada debido a fuerzas de deslizamiento lateral.

El deslizamiento lateral en ausencia de acción del timón provoca un impacto en el fuselaje y el empenaje , creando así un momento de guiñada contrarrestado únicamente por la rigidez direccional que tendería a apuntar el morro del avión hacia el viento en condiciones de vuelo horizontal. En condiciones de deslizamiento lateral con un ángulo de alabeo determinado, el morro tenderá a apuntar hacia la dirección del deslizamiento lateral incluso sin acción del timón, lo que provocará un vuelo en espiral descendente.${\displaystyle N_{\beta }}$

${\displaystyle N_{p}}$Momento de guiñada debido a la velocidad de giro.

La velocidad de alabeo genera sustentación de las aletas, lo que provoca un momento de guiñada y también altera de forma diferencial la sustentación de las alas, lo que afecta a la contribución de la resistencia inducida de cada ala, lo que provoca una (pequeña) contribución del momento de guiñada. El alabeo positivo generalmente produce valores positivos a menos que el empenaje sea anédrico o la aleta esté por debajo del eje de alabeo. Los componentes de fuerza lateral resultantes de las diferencias de sustentación del ala diédrica o anédrica tienen poco efecto porque el eje del ala normalmente está alineado de cerca con el centro de gravedad.${\displaystyle N_{p}}$${\displaystyle N_{p}}$

${\displaystyle N_{r}}$Momento de guiñada debido a la velocidad de guiñada.

La entrada de la velocidad de guiñada en cualquier ángulo de alabeo genera vectores de fuerza en el timón, las aletas y el fuselaje que dominan el momento de guiñada resultante. La guiñada también aumenta la velocidad del ala exterior mientras que reduce la velocidad del ala interior, con los cambios correspondientes en la resistencia que causan un momento de guiñada opuesto (pequeño). se opone a la rigidez direccional inherente que tiende a apuntar el morro del avión hacia el viento y siempre coincide con el signo de la entrada de la velocidad de guiñada.${\displaystyle N_{r}}$

${\displaystyle L_{\beta }}$Momento de balanceo debido al deslizamiento lateral.

Un ángulo de deslizamiento positivo genera una incidencia en el empenaje que puede causar un momento de alabeo positivo o negativo según su configuración. Para cualquier ángulo de deslizamiento distinto de cero, las alas diedras causan un momento de alabeo que tiende a devolver la aeronave a la horizontal, al igual que las alas en flecha hacia atrás. Con alas muy en flecha, el momento de alabeo resultante puede ser excesivo para todos los requisitos de estabilidad y se podría utilizar un ángulo anhédrico para compensar el efecto del momento de alabeo inducido por el barrido del ala.

${\displaystyle L_{r}}$Momento de balanceo debido a la velocidad de guiñada.

La guiñada aumenta la velocidad del ala exterior mientras reduce la velocidad de la interior, lo que provoca un momento de balanceo hacia el lado interior. La contribución de la aleta normalmente favorece este efecto de balanceo hacia el interior, a menos que se compense con un estabilizador anédrico por encima del eje de balanceo (o diedro por debajo del eje de balanceo).

${\displaystyle L_{p}}$Momento de balanceo debido a la velocidad de balanceo.

El alabeo crea fuerzas contrarrotatorias en las alas de babor y estribor, y también genera fuerzas similares en el empenaje. Estos efectos opuestos del momento de alabeo deben ser superados por la acción del alerón para mantener la velocidad de alabeo. Si el alabeo se detiene en un ángulo de alabeo distinto de cero, el momento de alabeo ascendente inducido por el deslizamiento lateral resultante debería devolver la aeronave a la horizontal, a menos que sea superado a su vez por el momento de alabeo descendente resultante de la velocidad de guiñada inducida por el deslizamiento lateral. La estabilidad longitudinal podría garantizarse o mejorarse minimizando este último efecto.${\displaystyle L_{\beta }}$ ${\displaystyle L_{r}}$

Dado que el balanceo holandés es un modo de manejo, análogo a la oscilación de cabeceo de período corto, se puede ignorar cualquier efecto que pueda tener sobre la trayectoria. La velocidad de giro r se compone de la tasa de cambio del ángulo de deslizamiento lateral y la velocidad de giro. Si tomamos esta última como cero, suponiendo que no hay efecto sobre la trayectoria, para el propósito limitado de estudiar el balanceo holandés:

${\displaystyle {\frac {d\beta }{dt}}=-r}$

Las ecuaciones de guiñada y balanceo, con las derivadas de estabilidad, se convierten en:

${\displaystyle C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p}$(guiñada)

${\displaystyle A{\frac {dp}{dt}}-E{\frac {dr}{dt}}=L_{\beta }\beta -L_{r}{\frac {d\beta }{dt}}+L_{p}p}$(rollo)

El momento de inercia debido a la aceleración del balanceo se considera pequeño en comparación con los términos aerodinámicos, por lo que las ecuaciones se convierten en:

${\displaystyle -C{\frac {d^{2}\beta }{dt^{2}}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p}$

${\displaystyle E{\frac {d^{2}\beta }{dt^{2}}}=L_{\beta }\beta -L_{r}{\frac {d\beta }{dt}}+L_{p}p}$

Esto se convierte en una ecuación de segundo orden que rige la velocidad de giro o el deslizamiento lateral:

${\displaystyle \left({\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}\right){\frac {d^{2}\beta }{dt^{2}}}+\left({\frac {L_{p}}{A}}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}\right){\frac {d\beta }{dt}}-\left({\frac {L_{p}}{A}}{\frac {N_{\beta }}{C}}-{\frac {L_{\beta }}{A}}{\frac {N_{p}}{C}}\right)\beta =0}$

La ecuación para la velocidad de alabeo es idéntica, pero el ángulo de alabeo (phi) viene dado por:${\displaystyle \phi }$

${\displaystyle {\frac {d\phi }{dt}}=p}$

Si p es un movimiento armónico simple amortiguado, también lo es , pero el alabeo debe estar en cuadratura con la velocidad de alabeo y, por lo tanto, también con el deslizamiento lateral. El movimiento consiste en oscilaciones en alabeo y guiñada, con el movimiento de alabeo retrasado 90 grados con respecto a la guiñada. Las puntas de las alas trazan trayectorias elípticas.${\displaystyle \phi }$

La estabilidad requiere que los términos " rigidez " y "amortiguación" sean positivos. Estos son:

${\displaystyle {\frac {{\frac {L_{p}}{A}}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}}$(mojadura)

${\displaystyle {\frac {{\frac {L_{\beta }}{A}}{\frac {N_{p}}{C}}-{\frac {L_{p}}{A}}{\frac {N_{\beta }}{C}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}}$ (rigidez)

El denominador está dominado por , la derivada de amortiguación del balanceo, que siempre es negativa, por lo que los denominadores de estas dos expresiones serán positivos.${\displaystyle L_{p}}$

Teniendo en cuenta el término "rigidez": será positivo porque siempre es negativo y es positivo por diseño. suele ser negativo, mientras que es positivo. Un diedro excesivo puede desestabilizar el alabeo holandés, por lo que las configuraciones con alas muy en flecha requieren un anhedro para compensar la contribución del alabe en flecha .${\displaystyle -L_{p}N_{\beta }}$${\displaystyle L_{p}}$${\displaystyle N_{\beta }}$${\displaystyle L_{\beta }}$${\displaystyle N_{p}}$${\displaystyle L_{\beta }}$

El término de amortiguación está dominado por el producto de las derivadas de amortiguación de balanceo y de amortiguación de guiñada, ambas son negativas, por lo que su producto es positivo. Por lo tanto, el balanceo holandés debería estar amortiguado.

El movimiento va acompañado de un ligero movimiento lateral del centro de gravedad y un análisis más "exacto" introducirá términos en etc. En vista de la precisión con la que se pueden calcular las derivadas de estabilidad, esto es una pedantería innecesaria, que sirve para oscurecer la relación entre la geometría y el manejo de la aeronave, que es el objetivo fundamental de este artículo.${\displaystyle Y_{\beta }}$

Al mover la palanca hacia los lados y devolverla al centro se produce un cambio neto en la orientación del balanceo.

El movimiento de balanceo se caracteriza por la ausencia de estabilidad natural, no existen derivadas de estabilidad que generen momentos en respuesta al ángulo de balanceo inercial. Una perturbación del balanceo induce una velocidad de balanceo que solo se cancela mediante la intervención del piloto o del piloto automático . Esto ocurre con cambios insignificantes en la velocidad de deslizamiento lateral o de guiñada, por lo que la ecuación de movimiento se reduce a:

${\displaystyle A{\frac {dp}{dt}}=L_{p}p.}$

${\displaystyle L_{p}}$es negativo, por lo que la velocidad de alabeo disminuirá con el tiempo. La velocidad de alabeo se reduce a cero, pero no hay control directo sobre el ángulo de alabeo.

Si se mantiene la palanca quieta al comenzar con las alas casi niveladas, el avión generalmente tendrá una tendencia a desviarse gradualmente hacia un lado de la trayectoria de vuelo recta. Este es el modo espiral (ligeramente inestable) . ^{[ cita requerida ]}

Al estudiar la trayectoria, lo que interesa es la dirección del vector de velocidad, más que la del cuerpo. La dirección del vector de velocidad cuando se proyecta sobre la horizontal se denomina trayectoria, denotada por ( mu ). La orientación del cuerpo se denomina rumbo, denotada por ( psi ). La ecuación de fuerza del movimiento incluye un componente de peso: ^{[ cita requerida ]}${\displaystyle \mu }$${\displaystyle \psi }$

${\displaystyle {\frac {d\mu }{dt}}={\frac {Y}{mU}}+{\frac {g}{U}}\phi }$

donde g es la aceleración gravitacional y U es la velocidad.

Incluidas las derivadas de estabilidad:

${\displaystyle {\frac {d\mu }{dt}}={\frac {Y_{\beta }}{mU}}\beta +{\frac {Y_{r}}{mU}}r+{\frac {Y_{p}}{mU}}p+{\frac {g}{U}}\phi }$

Se espera que las velocidades de balanceo y de guiñada sean pequeñas, por lo que se ignorarán las contribuciones de y .${\displaystyle Y_{r}}$${\displaystyle Y_{p}}$

La velocidad de deslizamiento lateral y de alabeo varían gradualmente, por lo que se ignoran sus derivadas temporales. Las ecuaciones de guiñada y alabeo se reducen a:

${\displaystyle N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0}$ (guiñada)

${\displaystyle L_{\beta }\beta +L_{r}{\frac {d\mu }{dt}}+L_{p}p=0}$(rollo)

Resolviendo para y p :${\displaystyle \beta }$

${\displaystyle \beta ={\frac {(L_{r}N_{p}-L_{p}N_{r})}{(L_{p}N_{\beta }-N_{p}L_{\beta })}}{\frac {d\mu }{dt}}}$

${\displaystyle p={\frac {(L_{\beta }N_{r}-L_{r}N_{\beta })}{(L_{p}N_{\beta }-N_{p}L_{\beta })}}{\frac {d\mu }{dt}}}$

Sustituyendo el deslizamiento lateral y la velocidad de balanceo en la ecuación de fuerza, se obtiene una ecuación de primer orden en el ángulo de balanceo:

${\displaystyle {\frac {d\phi }{dt}}=mg{\frac {(L_{\beta }N_{r}-N_{\beta }L_{r})}{mU(L_{p}N_{\beta }-N_{p}L_{\beta })-Y_{\beta }(L_{r}N_{p}-L_{p}N_{r})}}\phi }$

Se trata de un crecimiento o decrecimiento exponencial , dependiendo de si el coeficiente de es positivo o negativo. El denominador suele ser negativo, lo que requiere que ambos productos sean positivos. Esto entra en conflicto directo con el requisito de estabilidad del balanceo holandés, y es difícil diseñar una aeronave para la que tanto el balanceo holandés como el modo espiral sean inherentemente estables. ^{[ cita requerida ]}${\displaystyle \phi }$${\displaystyle L_{\beta }N_{r}>N_{\beta }L_{r}}$

Dado que el modo espiral tiene una constante de tiempo larga, el piloto puede intervenir para estabilizarlo de manera efectiva, pero un avión con un balanceo holandés inestable sería difícil de volar. Es habitual diseñar el avión con un modo de balanceo holandés estable, pero un modo espiral ligeramente inestable. ^{[ cita requerida ]}

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2009) (Learn how and when to remove this message)

• NK Sinha y N Ananthkrishnan (2013), Dinámica de vuelo elemental con una introducción a los métodos de bifurcación y continuación , CRC Press, Taylor & Francis.
• Babister, AW (1980). Estabilidad y respuesta dinámica de aeronaves (1.ª ed.). Oxford: Pergamon Press. ISBN 978-0080247687.

• MIXR - plataforma de simulación de realidad mixta
• JSBsim, una biblioteca de software de control y dinámica de vuelo, independiente de la plataforma y de código abierto, en C++