Disco aireado

En óptica , el disco de Airy (o disco de Airy ) y el patrón de Airy son descripciones del punto de luz mejor enfocado que puede crear una lente perfecta con una apertura circular , limitada por la difracción de la luz. El disco de Airy es importante en física , óptica y astronomía .

El patrón de difracción resultante de una abertura circular uniformemente iluminada tiene una región central brillante , conocida como disco de Airy, que junto con la serie de anillos concéntricos que la rodean se denomina patrón de Airy. Ambos reciben su nombre de George Biddell Airy . El fenómeno del disco y los anillos ya se conocía antes de Airy; John Herschel describió la apariencia de una estrella brillante vista a través de un telescopio con gran aumento en un artículo de 1828 sobre la luz para la Enciclopedia Metropolitana :

...la estrella se ve entonces (en circunstancias favorables de atmósfera tranquila, temperatura uniforme, etc.) como un disco planetario perfectamente redondo y bien definido, rodeado por dos, tres o más anillos alternativamente oscuros y brillantes, que, si se observan con atención, se ven ligeramente coloreados en sus bordes. Se suceden unos a otros a intervalos casi iguales alrededor del disco central.... ^[1]

Airy escribió el primer tratamiento teórico completo que explica el fenómeno (su libro "Sobre la difracción de un objeto de vidrio con apertura circular" de 1835). ^[2]

Matemáticamente, el patrón de difracción se caracteriza por la longitud de onda de la luz que ilumina la abertura circular y el tamaño de la abertura. La apariencia del patrón de difracción se caracteriza además por la sensibilidad del ojo u otro detector utilizado para observar el patrón.

La aplicación más importante de este concepto se da en cámaras , microscopios y telescopios . Debido a la difracción, el punto más pequeño en el que una lente o un espejo puede enfocar un haz de luz es del tamaño del disco de Airy. Incluso si se pudiera fabricar una lente perfecta, todavía hay un límite para la resolución de una imagen creada por dicha lente. Un sistema óptico en el que la resolución ya no está limitada por imperfecciones en las lentes sino solo por la difracción se dice que está limitado por difracción .

Lejos de la apertura, el ángulo en el que se produce el primer mínimo, medido desde la dirección de la luz entrante, viene dado por la fórmula aproximada:

$${\displaystyle \sin \theta \approx 1.22{\frac {\lambda }{d}}}$$

o, para ángulos pequeños, simplemente

$${\displaystyle \theta \aproximadamente 1,22{\frac {\lambda }{d}},}$$

donde está en radianes, es la longitud de onda de la luz en metros y es el diámetro de la abertura en metros. El ancho total en la mitad del máximo está dado por${\estilo de visualización \theta}$${\estilo de visualización \lambda}$${\estilo de visualización {d}}$${\displaystyle \theta _{\mathrm {FWHM} }=1.029{\frac {\lambda }{d}}.}$

Airy escribió esta relación como

$${\displaystyle s={\frac {2.76}{a}},}$$

donde era el ángulo del primer mínimo en segundos de arco, era el radio de la apertura en pulgadas y se supuso que la longitud de onda de la luz era 0,000022 pulgadas (560 nm; la media de las longitudes de onda visibles). ^[3] Esto es igual a la resolución angular de una apertura circular. El criterio de Rayleigh para resolver apenas dos objetos que son fuentes puntuales de luz, como las estrellas vistas a través de un telescopio, es que el centro del disco de Airy para el primer objeto se produce en el primer mínimo del disco de Airy del segundo. Esto significa que la resolución angular de un sistema limitado por difracción está dada por las mismas fórmulas.${\estilo de visualización {s}}$${\estilo de visualización {a}}$

Sin embargo, mientras que el ángulo en el que se produce el primer mínimo (que a veces se describe como el radio del disco de Airy) depende sólo de la longitud de onda y el tamaño de la apertura, la apariencia del patrón de difracción variará con la intensidad (brillo) de la fuente de luz. Debido a que cualquier detector (ojo, película, digital) utilizado para observar el patrón de difracción puede tener un umbral de intensidad para la detección, el patrón de difracción completo puede no ser evidente. En astronomía, los anillos exteriores con frecuencia no son evidentes incluso en una imagen muy ampliada de una estrella. Puede ser que ninguno de los anillos sea evidente, en cuyo caso la imagen de la estrella aparece como un disco (máximo central solamente) en lugar de como un patrón de difracción completo. Además, las estrellas más débiles aparecerán como discos más pequeños que las estrellas más brillantes, porque menos de su máximo central alcanza el umbral de detección. ^[4] Aunque en teoría todas las estrellas u otras "fuentes puntuales" de una longitud de onda dada y vistas a través de una apertura dada tienen el mismo radio de disco de Airy caracterizado por la ecuación anterior (y el mismo tamaño de patrón de difracción), diferenciándose solo en intensidad, la apariencia es que las fuentes más débiles aparecen como discos más pequeños, y las fuentes más brillantes aparecen como discos más grandes. ^[5] Esto fue descrito por Airy en su trabajo original: ^[6]

La rápida disminución de la luz en los anillos sucesivos explicará suficientemente la visibilidad de dos o tres anillos con una estrella muy brillante y la no visibilidad de anillos con una estrella débil. La diferencia de los diámetros de las manchas centrales (o discos espurios) de diferentes estrellas ... también se explica plenamente. Así, el radio del disco espurio de una estrella débil, donde la luz de menos de la mitad de la intensidad de la luz central no hace impresión en el ojo, está determinado por [ s = 1,17 / a ], mientras que el radio del disco espurio de una estrella brillante, donde la luz de 1/10 de la intensidad de la luz central es sensible, está determinado por [ s = 1,97 / a ].

A pesar de esta característica del trabajo de Airy, el radio del disco de Airy a menudo se da simplemente como el ángulo del primer mínimo, incluso en los libros de texto estándar. ^[7] En realidad, el ángulo del primer mínimo es un valor límite para el tamaño del disco de Airy, y no un radio definido.

Si dos objetos captados por una cámara están separados por un ángulo lo suficientemente pequeño como para que sus discos de Airy en el detector de la cámara comiencen a superponerse, los objetos ya no pueden separarse claramente en la imagen y comienzan a difuminarse. Se dice que dos objetos están resueltos cuando el máximo del primer patrón de Airy cae sobre el primer mínimo del segundo patrón de Airy ( criterio de Rayleigh ).

Por lo tanto, la separación angular más pequeña que pueden tener dos objetos antes de que se difuminen significativamente se da como se indicó anteriormente por$${\displaystyle \sin \theta = 1,22\,{\frac {\lambda }{d}}.}$$

Por lo tanto, la capacidad del sistema para resolver los detalles está limitada por la relación λ/ d . Cuanto mayor sea la apertura para una longitud de onda determinada, más finos serán los detalles que se pueden distinguir en la imagen.

Esto también se puede expresar como donde es la separación de las imágenes de los dos objetos en la película, y es la distancia desde la lente a la película. Si tomamos la distancia desde la lente a la película como aproximadamente igual a la longitud focal de la lente, encontramos pero es el número f de una lente. Una configuración típica para usar en un día nublado sería$${\displaystyle {\frac {x}{f}}=1.22\,{\frac {\lambda }{d}},}$$${\estilo de visualización x}$${\estilo de visualización f}$$${\displaystyle x=1.22\,{\frac {\lambda \,f}{d}},}$$${\displaystyle {\frac {f}{d}}}$f /8(ver regla de Sunny 16 ). Para el violeta, la luz visible de longitud de onda más corta, la longitud de onda λ es de aproximadamente 420 nanómetros (ver células cónicas para la sensibilidad de las células cónicas S). Esto da un valor para de aproximadamente 4 μm. En una cámara digital, hacer que los píxeles del sensor de imagen sean más pequeños que la mitad de este valor (un píxel para cada objeto, uno para cada espacio entre ellos) no aumentaría significativamente la resolución de la imagen capturada . Sin embargo, puede mejorar la imagen final mediante un sobremuestreo, lo que permite la reducción de ruido.${\estilo de visualización x}$

El número f más rápido para el ojo humano es de aproximadamente 2,1 ^[8], que corresponde a una función de dispersión de puntos limitada por difracción con un diámetro de aproximadamente 1 μm. Sin embargo, en este número f, la aberración esférica limita la agudeza visual, mientras que un diámetro de pupila de 3 mm (f/5,7) se aproxima a la resolución alcanzada por el ojo humano. ^[9] La densidad máxima de conos en la fóvea humana es de aproximadamente 170 000 por milímetro cuadrado ^[10] , lo que implica que el espaciado de los conos en el ojo humano es de aproximadamente 2,5 μm, aproximadamente el diámetro de la función de dispersión de puntos en f/5.

Un haz láser circular con una intensidad uniforme a lo largo del círculo (un haz de superficie plana) enfocado por una lente formará un patrón de disco de Airy en el foco. El tamaño del disco de Airy determina la intensidad del láser en el foco.

Algunas miras de puntería para armas (por ejemplo, FN FNC ) requieren que el usuario alinee una mira de mirilla (la mira trasera, cercana, es decir, que estará fuera de foco) con una punta (que debe estar enfocada y superpuesta al objetivo) en el extremo del cañón. Al mirar a través de la mira de mirilla, el usuario notará un disco Airy que ayudará a centrar la mira sobre el pasador. ^[11]

La luz proveniente de una abertura circular iluminada uniformemente (o de un haz uniforme y plano) exhibirá un patrón de difracción de Airy lejos de la abertura debido a la difracción de Fraunhofer (difracción de campo lejano).

Las condiciones para estar en el campo lejano y exhibir un patrón de Airy son: la luz entrante que ilumina la abertura es una onda plana (sin variación de fase a lo largo de la abertura), la intensidad es constante en el área de la abertura y la distancia desde la abertura donde se observa la luz difractada (la distancia de la pantalla) es grande en comparación con el tamaño de la abertura, y el radio de la abertura no es mucho mayor que la longitud de onda de la luz. Las dos últimas condiciones se pueden escribir formalmente como${\estilo de visualización R}$${\estilo de visualización a}$${\estilo de visualización \lambda}$${\displaystyle R>a^{2}/\lambda .}$

En la práctica, las condiciones para una iluminación uniforme se pueden cumplir colocando la fuente de iluminación lejos de la abertura. Si no se cumplen las condiciones para el campo lejano (por ejemplo, si la abertura es grande), el patrón de difracción de Airy de campo lejano también se puede obtener en una pantalla mucho más cercana a la abertura utilizando una lente justo después de la abertura (o la lente misma puede formar la abertura). El patrón de Airy se formará entonces en el foco de la lente en lugar de en el infinito.

Por lo tanto, el punto focal de un rayo láser circular uniforme (un rayo plano) enfocado por una lente también será un patrón de Airy.

En una cámara o un sistema de imágenes, un objeto que se encuentra lejos se proyecta sobre la película o el plano del detector a través de la lente del objetivo, y el patrón de difracción de campo lejano se observa en el detector. La imagen resultante es una convolución de la imagen ideal con el patrón de difracción de Airy debido a la difracción de la apertura del iris o debido al tamaño finito de la lente. Esto conduce a la resolución finita de un sistema de lentes descrito anteriormente.

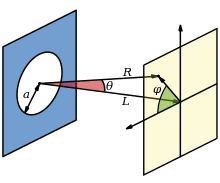
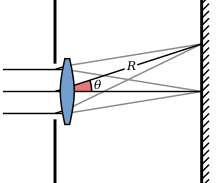
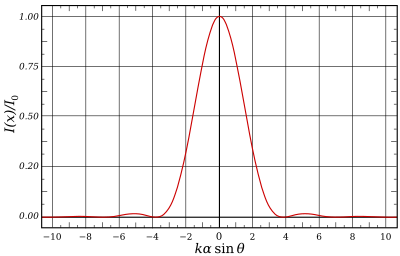
La intensidad del patrón de Airy sigue el patrón de difracción de Fraunhofer de una apertura circular, dado por el módulo al cuadrado de la transformada de Fourier de la apertura circular:

$${\displaystyle I(\theta )=I_{0}\left[{\frac {2J_{1}(k\,a\sin \theta )}{k\,a\sin \theta }}\right]^{2}=I_{0}\left[{\frac {2J_{1}(x)}{x}}\right]^{2}}$$

donde es la intensidad máxima del patrón en el centro del disco de Airy, es la función de Bessel de primer tipo de orden uno, es el número de onda, es el radio de la apertura, y es el ángulo de observación, es decir, el ángulo entre el eje de la apertura circular y la línea entre el centro de la apertura y el punto de observación. donde q es la distancia radial desde el punto de observación al eje óptico y R es su distancia a la apertura. Tenga en cuenta que el disco de Airy dado por la expresión anterior solo es válido para R grande , donde se aplica la difracción de Fraunhofer ; el cálculo de la sombra en el campo cercano debe manejarse más bien utilizando la difracción de Fresnel .${\displaystyle I_{0}}$${\estilo de visualización J_{1}}$${\displaystyle k={2\pi }/{\lambda }}$${\displaystyle a}$${\displaystyle \theta }$${\displaystyle x=ka\sin \theta ={\frac {2\pi a}{\lambda }}{\frac {q}{R}},}$

Sin embargo, el patrón de Airy exacto aparece a una distancia finita si se coloca una lente en la abertura. En ese caso, el patrón de Airy estará perfectamente enfocado a la distancia dada por la longitud focal de la lente (suponiendo que la luz colimada incide en la abertura) dada por las ecuaciones anteriores.

Los ceros de están en De esto, se deduce que el primer anillo oscuro en el patrón de difracción ocurre donde o${\displaystyle J_{1}(x)}$${\displaystyle x=ka\sin \theta \approx 3.8317,7.0156,10.1735,13.3237,16.4706\dots .}$${\displaystyle ka\sin {\theta }=3.8317\dots ,}$

$${\displaystyle \sin \theta \approx {\frac {3.83}{ka}}={\frac {3.83\lambda }{2\pi a}}=1.22{\frac {\lambda }{2a}}=1.22{\frac {\lambda }{d}}.}$$

Si se utiliza una lente para enfocar el patrón de Airy a una distancia finita, entonces el radio del primer anillo oscuro en el plano focal está dado únicamente por la apertura numérica A (estrechamente relacionada con el número f ) por${\displaystyle q_{1}}$ $${\displaystyle q_{1}=R\sin \theta _{1}\approx 1.22{R}{\frac {\lambda }{d}}=1.22{\frac {\lambda }{2A}}}$$

donde la apertura numérica A es igual al radio de la apertura d /2 dividido por R', la distancia desde el centro del patrón de Airy hasta el borde de la apertura. Si consideramos la apertura de radio d /2 y la lente como una cámara (ver el diagrama anterior) que proyecta una imagen sobre un plano focal a una distancia f , la apertura numérica A está relacionada con el número f comúnmente citado N= f/d (relación entre la longitud focal y el diámetro de la lente) según

$${\displaystyle A={\frac {r}{R'}}={\frac {r}{\sqrt {f^{2}+r^{2}}}}={\frac {1}{\sqrt {4N^{2}+1}}};}$$

para N ≫1 simplemente se aproxima como Esto muestra que la mejor resolución de imagen posible de una cámara está limitada por la apertura numérica (y por lo tanto el número f) de su lente debido a la difracción .${\textstyle A\approx 1/2N.}$

El medio máximo del disco central de Airy (donde ) ocurre en el punto 1/e ² (donde ) ocurre en y el máximo del primer anillo ocurre en${\displaystyle 2J_{1}(x)/x=1/{\sqrt {2}}}$${\displaystyle x=1.61633995\dots ;}$${\displaystyle 2J_{1}(x)/x=1/{e}}$${\displaystyle x=2.58383899\dots ,}$${\displaystyle x=5.13562230\dots .}$

La intensidad en el centro del patrón de difracción está relacionada con la potencia total incidente en la apertura por ^[12]${\displaystyle I_{0}}$${\displaystyle P_{0}}$

$${\displaystyle I_{0}={\frac {\mathrm {E} _{A}^{2}A^{2}}{2R^{2}}}={\frac {P_{0}A}{\lambda ^{2}R^{2}}}}$$

donde es la intensidad de la fuente por unidad de área en la apertura, A es el área de la apertura ( ) y R es la distancia desde la apertura. En el plano focal de una lente, la intensidad en el máximo del primer anillo es aproximadamente el 1,75 % de la intensidad en el centro del disco de Airy.${\displaystyle \mathrm {E} }$${\displaystyle A=\pi a^{2}}$${\displaystyle I_{0}=(P_{0}A)/(\lambda ^{2}f^{2}).}$

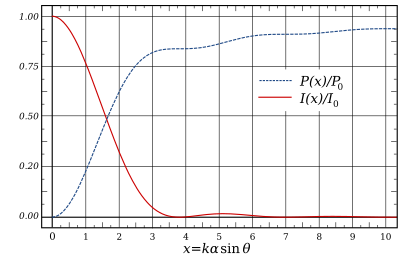
La expresión anterior se puede integrar para obtener la potencia total contenida en el patrón de difracción dentro de un círculo de tamaño determinado:${\displaystyle I(\theta )}$

$${\displaystyle P(\theta )=P_{0}[1-J_{0}^{2}(ka\sin \theta )-J_{1}^{2}(ka\sin \theta )]}$$

donde y son funciones de Bessel . Por lo tanto, las fracciones de la potencia total contenidas en el primer, segundo y tercer anillo oscuro (donde ) son 83,8 %, 91,0 % y 93,8 % respectivamente. ^[13]${\displaystyle J_{0}}$${\displaystyle J_{1}}$${\displaystyle J_{1}(ka\sin \theta )=0}$

El disco de Airy y el patrón de difracción se pueden calcular numéricamente a partir de primeros principios utilizando integrales de trayectoria de Feynman. ^[14]

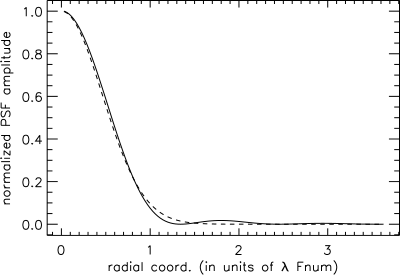
El patrón de Airy cae lentamente hasta cero a medida que aumenta la distancia desde el centro, y los anillos exteriores contienen una parte significativa de la intensidad integrada del patrón. Como resultado, el tamaño de punto de la raíz cuadrada media (RMS) no está definido (es decir, es infinito). Una medida alternativa del tamaño de punto es ignorar los anillos exteriores relativamente pequeños del patrón de Airy y aproximar el lóbulo central con un perfil gaussiano , de modo que

$${\displaystyle I(q)\approx I'_{0}\exp \left({\frac {-2q^{2}}{\omega _{0}^{2}}}\right)\ ,}$$

donde es la irradiancia en el centro del patrón, representa la distancia radial desde el centro del patrón y es el ancho RMS gaussiano (en una dimensión). Si igualamos la amplitud pico del patrón de Airy y el perfil gaussiano, es decir, y encontramos el valor de que da la aproximación óptima al patrón, obtenemos ^[15]${\displaystyle I'_{0}}$${\displaystyle q}$${\textstyle \omega _{0}}$${\displaystyle I'_{0}=I_{0},}$${\textstyle \omega _{0}}$

${\textstyle \omega _{0}\approx 0.84\lambda N\ ,}$

donde N es el número f . Si, por otro lado, deseamos asegurar que el perfil gaussiano tenga el mismo volumen que el patrón de Airy, entonces esto se convierte en

${\textstyle \omega _{0}\approx 0.90\lambda N\ .}$

En la teoría de la aberración óptica , es común describir un sistema de imágenes como limitado por difracción si el radio del disco de Airy es mayor que el tamaño de punto RMS determinado a partir del trazado geométrico de rayos (ver Diseño de lentes ópticas ). La aproximación del perfil gaussiano proporciona un medio alternativo de comparación: el uso de la aproximación anterior muestra que la cintura gaussiana de la aproximación gaussiana al disco de Airy es aproximadamente dos tercios del radio del disco de Airy, es decir, en oposición a${\textstyle \omega _{0}}$${\displaystyle 0.84\lambda N}$${\displaystyle 1.22\lambda N.}$

También se pueden derivar ecuaciones similares para el patrón de difracción oscurecido de Airy ^{[16] [17]} , que es el patrón de difracción de una abertura o haz anular, es decir, una abertura (haz) circular uniforme oscurecida por un bloque circular en el centro. Esta situación es relevante para muchos diseños comunes de telescopios reflectores que incorporan un espejo secundario, incluidos los telescopios newtonianos y los telescopios Schmidt-Cassegrain .

$${\displaystyle I(R)={\frac {I_{0}}{(1-\epsilon ^{2})^{2}}}\left({\frac {2J_{1}(x)}{x}}-{\frac {2\epsilon J_{1}(\epsilon x)}{x}}\right)^{2}}$$

donde es la razón de oscurecimiento de la apertura anular, o la razón entre el diámetro del disco oscurecedor y el diámetro de la apertura (haz). y x se define como se indica anteriormente: donde es la distancia radial en el plano focal desde el eje óptico, es la longitud de onda y es el número f del sistema. La energía fraccionaria encerrada (la fracción de la energía total contenida dentro de un círculo de radio centrado en el eje óptico en el plano focal) se expresa entonces mediante:${\displaystyle \epsilon }$${\displaystyle \left(0\leq \epsilon <1\right),}$${\displaystyle x=ka\sin(\theta )\approx {\frac {\pi R}{\lambda N}}}$${\displaystyle R}$${\displaystyle \lambda }$${\displaystyle N}$${\displaystyle R}$

$${\displaystyle E(R)={\frac {1}{(1-\epsilon ^{2})}}\left(1-J_{0}^{2}(x)-J_{1}^{2}(x)+\epsilon ^{2}\left[1-J_{0}^{2}(\epsilon x)-J_{1}^{2}(\epsilon x)\right]-4\epsilon \int _{0}^{x}{\frac {J_{1}(t)J_{1}(\epsilon t)}{t}}\,dt\right)}$$

Para que las fórmulas se reduzcan a las versiones no oscurecidas anteriores.${\displaystyle \epsilon \rightarrow 0}$

El efecto práctico de tener una obstrucción central en un telescopio es que el disco central se vuelve ligeramente más pequeño y el primer anillo brillante se vuelve más brillante a expensas del disco central. Esto se vuelve más problemático con telescopios de distancia focal corta que requieren espejos secundarios más grandes. ^[18]

Un haz láser circular con un perfil de intensidad uniforme, enfocado por una lente, formará un patrón de Airy en el plano focal de la lente. La intensidad en el centro del foco será donde es la potencia total del haz, es el área del haz ( es el diámetro del haz), es la longitud de onda y es la distancia focal de la lente.${\displaystyle I_{0,Airy}=(P_{0}A)/(\lambda ^{2}f^{2})}$${\displaystyle P_{0}}$${\displaystyle A=\pi D^{2}/4}$${\displaystyle D}$${\displaystyle \lambda }$${\displaystyle f}$

Un haz gaussiano transmitido a través de una abertura dura se verá recortado. Se pierde energía y se produce una difracción de borde, lo que aumenta efectivamente la divergencia. Debido a estos efectos, existe un diámetro del haz gaussiano que maximiza la intensidad en el campo lejano. Esto ocurre cuando el diámetro del haz gaussiano es el 89 % del diámetro de la abertura y la intensidad en el eje en el campo lejano será el 81 % de la producida por un perfil de intensidad uniforme. ^[19]${\displaystyle 1/e^{2}}$

La integral de Fourier de la sección transversal circular de radio es${\displaystyle a}$

${\displaystyle \int _{0}^{a}rdr\int _{0}^{2\pi }d\phi e^{i{\vec {k}}\cdot {\vec {r}}}=\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi e^{ikr\cos \phi }=2\int _{0}^{a}rdr\int _{0}^{\pi }d\phi \cos(kr\cos \phi )=2\pi \int _{0}^{a}rdrJ_{0}(kr)=2\pi {\frac {a}{k}}J_{1}(kr).}$

Este es el caso especial de la integral de Fourier de la sección transversal elíptica con semiejes y : ^[20]${\displaystyle a}$${\displaystyle b}$

${\displaystyle \int _{x^{2}/a^{2}+y^{2}/b^{2}\leq 1}e^{ik_{x}x}e^{ik_{y}y}dxdy=2\pi {\frac {ab}{c}}J_{1}(c)}$

dónde

${\displaystyle c\equiv {\sqrt {(k_{x}a)^{2}+(k_{y}b)^{2}}}.}$

• Astronomía amateur
• Apodización
• Difracción de Fraunhofer
• Bloom (efecto sombreador)
• Anillos de Newton
• Unidad óptica
• Función de dispersión de puntos
• Anillo Debye-Scherrer
• Relación de Strehl
• Patrón moteado

• Michael W. Davidson . "Conceptos y fórmulas en microscopía: resolución".Nikon MicroscopyU (sitio web).
  • Kenneth R. Spring; Brian O. Flynn y Michael W. Davidson. "Formación de imágenes: apertura numérica y resolución de imágenes" . Consultado el 15 de junio de 2006 .(Tutorial interactivo de Java) Expresiones moleculares (sitio web).
  • Kenneth R. Spring; Brian O. Flynn y Michael W. Davidson. "Formación de imágenes: formación de patrones de Airy" . Consultado el 15 de junio de 2006 .(Tutorial interactivo de Java) Expresiones moleculares .
• Paul Padley. "Difracción desde una apertura circular"., Connexions (sitio web), 8 de noviembre de 2005. – Detalles matemáticos para derivar la fórmula anterior.
• "El disco aéreo: una explicación de qué es y por qué no puedes evitarlo", Oldham Optical UK .
• Weisstein, Eric W. "Ceros de la función de Bessel". MathWorld .
• "Análisis extendido de Nijboer-Zernike (ENZ) y recuperación de aberraciones".