Hemodinámica
La hemodinámica o hemodinámica es la dinámica del flujo sanguíneo . El sistema circulatorio está controlado por mecanismos homeostáticos de autorregulación , al igual que los circuitos hidráulicos están controlados por sistemas de control . La respuesta hemodinámica monitorea y se ajusta continuamente a las condiciones del cuerpo y su entorno. La hemodinámica explica las leyes físicas que rigen el flujo de sangre en los vasos sanguíneos .
El flujo sanguíneo asegura el transporte de nutrientes , hormonas , productos metabólicos de desecho, oxígeno y dióxido de carbono por todo el cuerpo para mantener el metabolismo a nivel celular , la regulación del pH , la presión osmótica y la temperatura de todo el cuerpo y la protección contra daños microbianos y mecánicos. [1]
La sangre es un fluido no newtoniano y su estudio es más eficaz mediante la reología que mediante la hidrodinámica. Como los vasos sanguíneos no son tubos rígidos, la hidrodinámica clásica y la mecánica de fluidos basada en el uso de viscosímetros clásicos no son capaces de explicar la hemodinámica. [2]
El estudio del flujo sanguíneo se llama hemodinámica, y el estudio de las propiedades del flujo sanguíneo se llama hemorreología .
Sangre
La sangre es un líquido complejo. Está compuesta de plasma y elementos formes . El plasma contiene un 91,5 % de agua, un 7 % de proteínas y un 1,5 % de otros solutos. Los elementos formes son las plaquetas , los glóbulos blancos y los glóbulos rojos . La presencia de estos elementos formes y su interacción con las moléculas del plasma son las principales razones por las que la sangre difiere tanto de los fluidos newtonianos ideales. [1]
Viscosidad del plasma
El plasma sanguíneo normal se comporta como un fluido newtoniano a velocidades fisiológicas de cizallamiento. Los valores típicos de la viscosidad del plasma humano normal a 37 °C son 1,4 mN·s/m 2 . [3] La viscosidad del plasma normal varía con la temperatura de la misma manera que la de su disolvente, el agua [4] ; un cambio de 3 °C en la temperatura en el rango fisiológico (36,5 °C a 39,5 °C) reduce la viscosidad del plasma en aproximadamente un 10 %. [5]
Presión osmótica del plasma
La presión osmótica de una solución está determinada por el número de partículas presentes y por la temperatura . Por ejemplo, una solución 1 molar de una sustancia contiene6,022 × 10 23 moléculas por litro de esa sustancia y a 0 °C tiene una presión osmótica de 2,27 MPa (22,4 atm). La presión osmótica del plasma afecta la mecánica de la circulación de varias maneras. Una alteración de la diferencia de presión osmótica a través de la membrana de una célula sanguínea provoca un desplazamiento del agua y un cambio del volumen celular. Los cambios en la forma y la flexibilidad afectan las propiedades mecánicas de la sangre entera. Un cambio en la presión osmótica del plasma altera el hematocrito, es decir, la concentración de volumen de glóbulos rojos en la sangre entera al redistribuir el agua entre los espacios intravasculares y extravasculares. Esto a su vez afecta la mecánica de la sangre entera. [6]
Glóbulos rojos
El glóbulo rojo es muy flexible y tiene forma bicóncava. Su membrana tiene un módulo de Young en la región de 106 Pa . La deformación en los glóbulos rojos es inducida por la tensión de corte. Cuando se corta una suspensión, los glóbulos rojos se deforman y giran debido al gradiente de velocidad, y la tasa de deformación y giro depende de la tasa de corte y la concentración. Esto puede influir en la mecánica de la circulación y puede complicar la medición de la viscosidad sanguínea . Es cierto que en un flujo en estado estacionario de un fluido viscoso a través de un cuerpo esférico rígido sumergido en el fluido, donde asumimos que la inercia es despreciable en tal flujo, se cree que la fuerza gravitacional descendente de la partícula está equilibrada por la fuerza de arrastre viscosa. A partir de este equilibrio de fuerzas, se puede demostrar que la velocidad de caída está dada por la ley de Stokes [ cita requerida ]
- [6]
Donde a es el radio de la partícula, ρ p , ρ f son respectivamente la densidad de la partícula y del fluido μ es la viscosidad del fluido, g es la aceleración gravitacional. De la ecuación anterior podemos ver que la velocidad de sedimentación de la partícula depende del cuadrado del radio. Si la partícula se libera desde el reposo en el fluido , su velocidad de sedimentación U s aumenta hasta que alcanza el valor constante llamado velocidad terminal (U), como se muestra arriba. [ cita requerida ]
Hemodilución
La hemodilución es la dilución de la concentración de glóbulos rojos y componentes del plasma mediante la sustitución parcial de la sangre con coloides o cristaloides . Es una estrategia para evitar la exposición de los pacientes a los posibles peligros de las transfusiones de sangre homóloga . [7] [8]
La hemodilución puede ser normovolémica, lo que implica la dilución de los componentes normales de la sangre mediante el uso de expansores. Durante la hemodilución normovolémica aguda (ANH), la sangre que se pierde posteriormente durante la cirugía contiene proporcionalmente menos glóbulos rojos por mililitro, lo que minimiza la pérdida intraoperatoria de toda la sangre. Por lo tanto, la sangre que pierde el paciente durante la cirugía en realidad no la pierde el paciente, ya que este volumen se purifica y se redirige al paciente. [ cita requerida ]
Por otra parte, la hemodilución hipervolémica (HVH) utiliza una expansión de volumen preoperatoria aguda sin extracción de sangre. Sin embargo, al elegir un fluido, se debe asegurar que, al mezclarlo, la sangre restante se comporte en la microcirculación como en el fluido sanguíneo original, conservando todas sus propiedades de viscosidad . [9]
Al presentar qué volumen de ANH debe aplicarse, un estudio sugiere un modelo matemático de ANH que calcula el máximo ahorro posible de RCM utilizando ANH, dado el peso del paciente H i y H m . [ cita requerida ]
Para mantener la normovolemia, la sangre autóloga extraída debe ser reemplazada simultáneamente por un hemodiluido adecuado. Lo ideal es lograrlo mediante una transfusión de intercambio isovolémica de un sustituto de plasma con una presión osmótica coloidal (OP). Un coloide es un líquido que contiene partículas lo suficientemente grandes como para ejercer una presión oncótica a través de la membrana microvascular. Al debatir el uso de coloide o cristaloide, es imperativo pensar en todos los componentes de la ecuación de Starling:
Para identificar el hematocrito mínimo seguro deseable para un paciente determinado es útil la siguiente ecuación: [ cita requerida ]
donde EBV es el volumen de sangre estimado ; en este modelo se utilizaron 70 mL/kg y H i (hematocrito inicial) es el hematocrito inicial del paciente. De la ecuación anterior se desprende claramente que el volumen de sangre extraído durante la ANH hasta el H m es el mismo que el de BL s . La cantidad de sangre que se debe extraer suele basarse en el peso, no en el volumen. La cantidad de unidades que se deben extraer para hemodiluir hasta el hematocrito máximo seguro (ANH) se puede encontrar mediante
Esto se basa en el supuesto de que cada unidad extraída por hemodilución tiene un volumen de 450 mL (el volumen real de una unidad variará un poco ya que la finalización de la recolección depende del peso y no del volumen). El modelo supone que el valor de hemodilución es igual a la H m antes de la cirugía, por lo tanto, la retransfusión de sangre obtenida por hemodilución debe comenzar cuando comienza la SBL. El RCM disponible para la retransfusión después de ANH (RCMm) se puede calcular a partir de la H i del paciente y el hematocrito final después de la hemodilución ( H m ).
El SBL máximo que es posible cuando se utiliza ANH sin caer por debajo de Hm(BLH) se encuentra asumiendo que toda la sangre extraída durante ANH se devuelve al paciente a una velocidad suficiente para mantener el hematocrito en el nivel mínimo seguro.
Si se utiliza ANH siempre que el SBL no supere el BL H, no habrá necesidad de transfusión sanguínea. De lo anterior podemos concluir que, por lo tanto, el H no debe superar el s . Por lo tanto, la diferencia entre el BL H y el BL s es la pérdida de sangre quirúrgica incremental ( BL i ) posible cuando se utiliza ANH.
Cuando se expresa en términos del RCM
Donde RCM i es la masa de glóbulos rojos que debería administrarse utilizando sangre homóloga para mantener la H m si no se utiliza ANH y la pérdida de sangre es igual a BLH. [ cita requerida ]
El modelo utilizado supone el uso de ANH para un paciente de 70 kg con un volumen sanguíneo estimado de 70 ml/kg (4900 ml). Se evaluó un rango de H i y H m para comprender las condiciones en las que la hemodilución es necesaria para beneficiar al paciente. [10] [11]
Resultado
El resultado de los cálculos del modelo se presenta en una tabla que se incluye en el apéndice para un rango de H i de 0,30 a 0,50 con ANH realizada con hematocritos mínimos de 0,30 a 0,15. Dado un H i de 0,40, si se supone que H m es 0,25, entonces, a partir de la ecuación anterior, el recuento de RCM sigue siendo alto y no es necesaria ANH, si BL s no supera los 2303 ml, ya que el hematocrito no caerá por debajo de H m , aunque se deben extraer cinco unidades de sangre durante la hemodilución. En estas condiciones, para lograr el máximo beneficio de la técnica si se utiliza ANH, no se requerirá sangre homóloga para mantener la H m si la pérdida de sangre no supera los 2940 ml. En tal caso, la ANH puede ahorrar un máximo de 1,1 unidades equivalentes de glóbulos rojos empaquetados, y es necesaria una transfusión de sangre homóloga para mantener la H m , incluso si se utiliza ANH. [ cita requerida ] Este modelo se puede utilizar para identificar cuándo se puede utilizar ANH para un paciente determinado y el grado de ANH necesario para maximizar ese beneficio. [ cita requerida ]
Por ejemplo, si H i es 0,30 o menos, no es posible ahorrar una masa de glóbulos rojos equivalente a dos unidades de PRBC homólogo incluso si el paciente se hemodiluye a un H m de 0,15. Esto se debe a que de la ecuación de RCM, el RCM del paciente no alcanza la ecuación dada anteriormente. Si H i es 0,40, se deben extraer al menos 7,5 unidades de sangre durante la ANH, lo que da como resultado un H m de 0,20 para ahorrar dos unidades equivalentes. Claramente, cuanto mayor sea el H i y mayor sea el número de unidades extraídas durante la hemodilución, más eficaz será la ANH para prevenir la transfusión de sangre homóloga. El modelo aquí está diseñado para permitir que los médicos determinen dónde la ANH puede ser beneficiosa para un paciente según su conocimiento del H i , el potencial de SBL y una estimación del H m . Aunque el modelo utilizó un paciente de 70 kg, el resultado se puede aplicar a cualquier paciente. Para aplicar estos resultados a cualquier peso corporal, cualquiera de los valores BLs, BLH y ANHH o PRBC dados en la tabla deben multiplicarse por el factor que llamaremos T
Básicamente, el modelo considerado anteriormente está diseñado para predecir el RCM máximo que puede salvar la ANH. [ cita requerida ]
En resumen, la eficacia de la ANH se ha descrito matemáticamente mediante mediciones de la pérdida de sangre quirúrgica y la medición del flujo sanguíneo. Esta forma de análisis permite una estimación precisa de la eficiencia potencial de las técnicas y muestra la aplicación de la medición en el campo médico. [10]
Circulación sanguínea
Gasto cardíaco
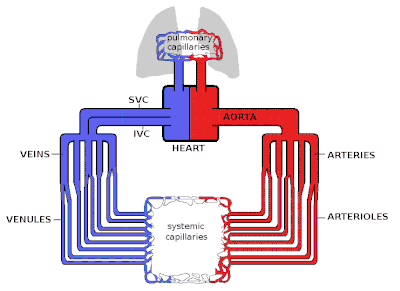
El corazón es el motor del sistema circulatorio y bombea sangre mediante contracción y relajación rítmicas. La velocidad del flujo sanguíneo que sale del corazón (a menudo expresada en l/min) se conoce como gasto cardíaco (GC).
La sangre que sale del corazón entra primero en la aorta , la arteria más grande del cuerpo. Luego procede a dividirse en arterias cada vez más pequeñas, luego en arteriolas y, finalmente, en capilares , donde se produce la transferencia de oxígeno. Los capilares se conectan a las vénulas y la sangre luego viaja de regreso a través de la red de venas hasta las venas cavas hacia el corazón derecho . La microcirculación (las arteriolas, los capilares y las vénulas) constituye la mayor parte del área del sistema vascular y es el sitio de la transferencia de O 2 , glucosa y sustratos enzimáticos hacia las células. El sistema venoso devuelve la sangre desoxigenada al corazón derecho, donde se bombea hacia los pulmones para oxigenarse y el CO 2 y otros desechos gaseosos se intercambian y expulsan durante la respiración. Luego, la sangre regresa al lado izquierdo del corazón, donde comienza el proceso nuevamente.
En un sistema circulatorio normal, el volumen de sangre que regresa al corazón cada minuto es aproximadamente igual al volumen que se bombea cada minuto (el gasto cardíaco). [12] Debido a esto, la velocidad del flujo sanguíneo a través de cada nivel del sistema circulatorio está determinada principalmente por el área transversal total de ese nivel.
El gasto cardíaco se determina mediante dos métodos. Uno es mediante la ecuación de Fick:
El otro método de termodilución es detectar el cambio de temperatura de un líquido inyectado en el puerto proximal de un Swan-Ganz al puerto distal.
El gasto cardíaco se expresa matemáticamente mediante la siguiente ecuación:
dónde
- CO = gasto cardíaco (L/seg)
- SV = volumen sistólico (ml)
- FC = frecuencia cardíaca (lpm)
El gasto cardíaco humano normal es de 5 a 6 l/min en reposo. No toda la sangre que entra en el ventrículo izquierdo sale del corazón. Lo que queda al final de la diástole (VTD) menos el volumen sistólico constituye el volumen sistólico final (VTS). [13]
Características anatómicas
El sistema circulatorio de las especies sometidas a presión sanguínea ortostática (como las serpientes arbóreas) ha evolucionado con características fisiológicas y morfológicas para superar la alteración circulatoria. Por ejemplo, en las serpientes arbóreas el corazón está más cerca de la cabeza, en comparación con las serpientes acuáticas. Esto facilita la perfusión sanguínea al cerebro. [14] [15]
Turbulencia
El flujo sanguíneo también se ve afectado por la uniformidad de los vasos, lo que da lugar a un flujo turbulento (caótico) o laminar (uniforme). La uniformidad se ve reducida por la acumulación de depósitos grasos en las paredes arteriales.
El número de Reynolds (denominado NR o Re) es una relación que ayuda a determinar el comportamiento de un fluido en un tubo, en este caso la sangre en el vaso.
La ecuación para esta relación adimensional se escribe como: [16]
- ρ : densidad de la sangre
- v : velocidad media de la sangre
- L : dimensión característica del recipiente, en este caso diámetro
- μ : viscosidad de la sangre
El número de Reynolds es directamente proporcional a la velocidad y al diámetro del tubo. Nótese que el NR es directamente proporcional a la velocidad media así como al diámetro. Un número de Reynolds menor a 2300 es flujo de fluido laminar, que se caracteriza por un movimiento de flujo constante, mientras que un valor mayor a 4000 se representa como flujo turbulento. [16] Debido a su radio más pequeño y velocidad más baja en comparación con otros vasos, el número de Reynolds en los capilares es muy bajo, lo que resulta en flujo laminar en lugar de turbulento. [17]
Velocidad
A menudo se expresa en cm/s. Este valor está inversamente relacionado con el área transversal total del vaso sanguíneo y también difiere por sección transversal, porque en condiciones normales el flujo sanguíneo tiene características laminares . Por esta razón, la velocidad del flujo sanguíneo es más rápida en el medio del vaso y más lenta en la pared del vaso. En la mayoría de los casos, se utiliza la velocidad media. [18] Hay muchas formas de medir la velocidad del flujo sanguíneo, como la microscopía videocapilar con análisis cuadro a cuadro o la anemometría láser Doppler . [19] Las velocidades de la sangre en las arterias son más altas durante la sístole que durante la diástole . Un parámetro para cuantificar esta diferencia es el índice de pulsatilidad ( PI ), que es igual a la diferencia entre la velocidad sistólica máxima y la velocidad diastólica mínima dividida por la velocidad media durante el ciclo cardíaco . Este valor disminuye con la distancia al corazón. [20]
| Tipos de vasos sanguíneos | Área total de la sección transversal | Velocidad de la sangre en cm/s |
|---|---|---|
| Aorta | 3–5 cm2 | 40 cm/s |
| Capilares | 4500–6000 cm2 | 0,03 cm/s [21] |
| Vena cava inferior y superior | 14 centímetros cuadrados | 15 cm/s |
Vasos sanguíneos
Resistencia vascular
La resistencia también está relacionada con el radio de los vasos, la longitud de los vasos y la viscosidad de la sangre.
En una primera aproximación basada en fluidos, como lo indica la ecuación de Hagen-Poiseuille . [16] La ecuación es la siguiente:
- ∆ P : caída/gradiente de presión
- μ : viscosidad
- l : longitud del tubo. En el caso de recipientes con longitudes infinitamente largas, l se reemplaza por el diámetro del recipiente.
- Q : caudal de la sangre en el vaso
- r : radio del buque
En un segundo enfoque, más realista de la resistencia vascular y que proviene de observaciones experimentales sobre flujos sanguíneos, según Thurston, [22] hay una capa de células de liberación de plasma en las paredes que rodean un flujo obstruido. Es una capa de fluido en la que a una distancia δ, la viscosidad η es una función de δ escrita como η(δ), y estas capas circundantes no se encuentran en el centro del vaso en el flujo sanguíneo real. En cambio, existe el flujo obstruido que es hiperviscoso porque contiene una alta concentración de glóbulos rojos. Thurston ensambló esta capa a la resistencia al flujo para describir el flujo sanguíneo por medio de una viscosidad η(δ) y un espesor δ de la capa de la pared.
La ley de resistencia sanguínea aparece como R adaptada al perfil del flujo sanguíneo:
- [22]
dónde
- R = resistencia al flujo sanguíneo
- c = coeficiente de flujo constante
- L = longitud del buque
- η(δ) = viscosidad de la sangre en la pared de la capa de células de liberación de plasma
- r = radio del vaso sanguíneo
- δ = distancia en la capa de células de liberación de plasma
La resistencia de la sangre varía en función de la viscosidad de la sangre y del tamaño de su flujo encapsulado (o flujo envolvente, ya que son complementarios en toda la sección del vaso), así como del tamaño de los vasos. Suponiendo que el flujo en el vaso es constante y laminar, el comportamiento de los vasos sanguíneos es similar al de una tubería. Por ejemplo, si p1 y p2 son presiones en los extremos del tubo, la caída/gradiente de presión es: [23]
Las arterias más grandes, incluidas todas las que son lo suficientemente grandes como para verlas sin aumento, son conductos con baja resistencia vascular (suponiendo que no haya cambios ateroscleróticos avanzados ) con altos caudales que generan solo pequeñas caídas de presión. Las arterias y arteriolas más pequeñas tienen mayor resistencia y confieren la principal caída de presión sanguínea a través de las arterias principales a los capilares del sistema circulatorio.

En las arteriolas la presión sanguínea es menor que en las arterias mayores. Esto se debe a las bifurcaciones, que causan una caída de presión. Cuantas más bifurcaciones haya, mayor será el área transversal total, por lo tanto la presión a través de la superficie cae. Esta es la razón por la que [ cita requerida ] las arteriolas tienen la caída de presión más alta. La caída de presión de las arteriolas es el producto del caudal y la resistencia: ∆P=Q xresistencia. La alta resistencia observada en las arteriolas, que influye en gran medida en el ∆ P, es el resultado de un radio más pequeño de aproximadamente 30 μm. [24] Cuanto menor sea el radio de un tubo, mayor será la resistencia al flujo de fluido.
Inmediatamente después de las arteriolas se encuentran los capilares. Siguiendo la lógica observada en las arteriolas, esperamos que la presión sanguínea sea menor en los capilares en comparación con las arteriolas. Dado que la presión es una función de la fuerza por unidad de área ( P = F / A ), cuanto mayor sea el área de superficie, menor será la presión cuando una fuerza externa actúe sobre ella. Aunque los radios de los capilares son muy pequeños, la red de capilares tiene la mayor área de superficie en la red vascular. Se sabe que tienen la mayor área de superficie (485 mm^2) en la red vascular humana. Cuanto mayor sea el área transversal total, menor será la velocidad media y la presión. [25]
Las sustancias llamadas vasoconstrictores pueden reducir el tamaño de los vasos sanguíneos, aumentando así la presión arterial. Los vasodilatadores (como la nitroglicerina ) aumentan el tamaño de los vasos sanguíneos, disminuyendo así la presión arterial.
Si la viscosidad de la sangre aumenta (se vuelve más espesa), el resultado es un aumento de la presión arterial. Ciertas enfermedades pueden cambiar la viscosidad de la sangre. Por ejemplo, la anemia (baja concentración de glóbulos rojos ) reduce la viscosidad, mientras que el aumento de la concentración de glóbulos rojos aumenta la viscosidad. Se pensaba que la aspirina y los fármacos " anticoagulantes " relacionados reducían la viscosidad de la sangre, pero en cambio los estudios han demostrado que actúan reduciendo la tendencia de la sangre a coagularse. [26]
Para determinar la resistencia vascular sistémica (RVS) se utiliza la fórmula para calcular todas las resistencias.
Esto se traduce para SVR en:
Dónde
- RVS = resistencia vascular sistémica (mmHg/L/min)
- PAM = presión arterial media (mmHg)
- PVC = presión venosa central (mmHg)
- CO = gasto cardíaco (L/min) [27]
Para obtener esto en unidades de madera, la respuesta se multiplica por 80.
La resistencia vascular sistémica normal está entre 900 y 1440 dinas/seg/cm−5. [28]
Tensión de la pared

Independientemente del sitio, la presión arterial está relacionada con la tensión de la pared del vaso según la ecuación de Young-Laplace (suponiendo que el espesor de la pared del vaso es muy pequeño en comparación con el diámetro del lumen ):
dónde
- P es la presión arterial
- t es el espesor de la pared
- r es el radio interior del cilindro.
- es la tensión del cilindro o "tensión circular".
Para que la suposición de paredes delgadas sea válida, el recipiente debe tener un espesor de pared de no más de aproximadamente una décima parte (a menudo citada como una vigésima parte) de su radio.
La tensión del cilindro , a su vez, es la fuerza media ejercida circunferencialmente (perpendicular tanto al eje como al radio del objeto) en la pared del cilindro, y puede describirse como:
dónde:
- F es la fuerza ejercida circunferencialmente sobre un área de la pared del cilindro que tiene las siguientes dos longitudes como lados:
- t es el espesor radial del cilindro
- l es la longitud axial del cilindro
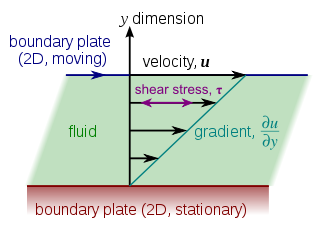
Estrés
Cuando se aplica una fuerza a un material, este comienza a deformarse o moverse. A medida que la fuerza necesaria para deformar un material (por ejemplo, para hacer que fluya un fluido) aumenta con el tamaño de la superficie del material A. [6] , la magnitud de esta fuerza F es proporcional al área A de la porción de la superficie. Por lo tanto, la cantidad (F/A) que es la fuerza por unidad de área se denomina tensión. La tensión de corte en la pared que está asociada con el flujo sanguíneo a través de una arteria depende del tamaño y la geometría de la arteria y puede variar entre 0,5 y 4 Pa . [29]
- .
En condiciones normales, para evitar la aterogénesis, la trombosis, la proliferación del músculo liso y la apoptosis endotelial, la tensión de corte mantiene su magnitud y dirección dentro de un rango aceptable. En algunos casos que ocurren debido al golpe de sangre, la tensión de corte alcanza valores mayores. Si bien la dirección de la tensión también puede cambiar por el flujo inverso, dependiendo de las condiciones hemodinámicas. Por lo tanto, esta situación puede conducir a la enfermedad aterosclerótica. [30]
Capacidad
Las venas se describen como los "vasos de capacitancia" del cuerpo porque más del 70% del volumen sanguíneo reside en el sistema venoso. Las venas son más flexibles que las arterias y se expanden para adaptarse a los cambios de volumen. [31]
Presión arterial
La presión sanguínea en la circulación se debe principalmente a la acción de bombeo del corazón. [32] La acción de bombeo del corazón genera un flujo sanguíneo pulsátil, que se conduce a las arterias, a través de la microcirculación y, finalmente, de regreso a través del sistema venoso al corazón. Durante cada latido del corazón, la presión arterial sistémica varía entre una presión máxima ( sistólica ) y una mínima ( diastólica ). [33] En fisiología, estas a menudo se simplifican en un valor, la presión arterial media (PAM) , que se calcula de la siguiente manera:
dónde:
- MAP = Presión arterial media
- DP = Presión arterial diastólica
- PP = Presión de pulso que es la presión sistólica menos la presión diastólica. [34]
Las diferencias en la presión arterial media son responsables del flujo sanguíneo de un lugar a otro en la circulación. La tasa de flujo sanguíneo medio depende tanto de la presión arterial como de la resistencia al flujo presentada por los vasos sanguíneos. La presión arterial media disminuye a medida que la sangre circulante se aleja del corazón a través de las arterias y capilares debido a las pérdidas viscosas de energía. La presión arterial media cae en toda la circulación, aunque la mayor parte de la caída ocurre a lo largo de las pequeñas arterias y arteriolas . [35] La gravedad afecta la presión arterial a través de fuerzas hidrostáticas (p. ej., al estar de pie), y las válvulas en las venas, la respiración y el bombeo por la contracción de los músculos esqueléticos también influyen en la presión arterial en las venas. [32]
La relación entre presión, flujo y resistencia se expresa en la siguiente ecuación: [12]
Aplicado al sistema circulatorio obtenemos:
dónde
- CO = gasto cardíaco (en L/min)
- PAM = presión arterial media (en mmHg), la presión promedio de la sangre cuando sale del corazón
- RAP = presión auricular derecha (en mmHg), la presión promedio de la sangre cuando regresa al corazón
- RVS = resistencia vascular sistémica (en mmHg * min/L)
Una forma simplificada de esta ecuación supone que la presión auricular derecha es aproximadamente 0:
La presión arterial ideal en la arteria braquial , donde los manguitos de presión arterial estándar miden la presión, es <120/80 mmHg. Otras arterias principales tienen niveles similares de registros de presión arterial, lo que indica disparidades muy bajas entre las arterias principales. En la arteria innominada, la lectura promedio es de 110/70 mmHg, la arteria subclavia derecha promedia 120/80 y la aorta abdominal es de 110/70 mmHg. [25] La presión relativamente uniforme en las arterias indica que estos vasos sanguíneos actúan como un reservorio de presión para los fluidos que se transportan dentro de ellos.
La presión desciende gradualmente a medida que la sangre fluye desde las arterias principales, a través de las arteriolas y los capilares, hasta que la sangre es impulsada hacia el corazón a través de las vénulas y las venas a través de la vena cava con la ayuda de los músculos. En cualquier caída de presión dada, el caudal está determinado por la resistencia al flujo sanguíneo. En las arterias, en ausencia de enfermedades, hay muy poca o ninguna resistencia a la sangre. El diámetro del vaso es el determinante principal para controlar la resistencia. En comparación con otros vasos más pequeños del cuerpo, la arteria tiene un diámetro mucho mayor (4 mm), por lo tanto, la resistencia es baja. [25]
El gradiente brazo-pierna (presión arterial) es la diferencia entre la presión arterial medida en los brazos y la medida en las piernas. Normalmente es inferior a 10 mmHg, [36] pero puede estar aumentado en casos de coartación de la aorta , por ejemplo. [36]
Importancia clínica
Monitoreo de presión
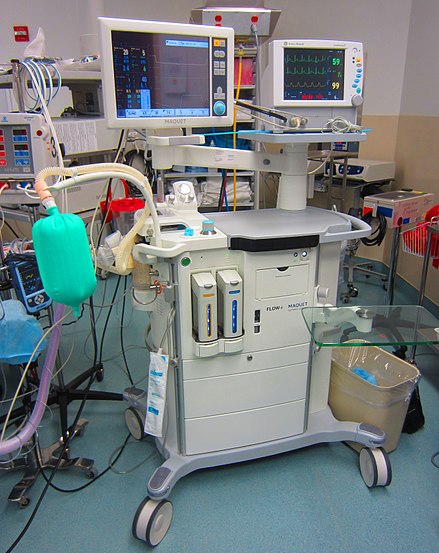
La monitorización hemodinámica es la observación de parámetros hemodinámicos a lo largo del tiempo, como la presión arterial y la frecuencia cardíaca . La presión arterial se puede controlar de forma invasiva a través de un conjunto de transductores de presión arterial insertado (que proporciona una monitorización continua) o de forma no invasiva midiendo repetidamente la presión arterial con un manguito de presión arterial inflable .
La hipertensión se diagnostica por la presencia de presiones arteriales de 140/90 o más durante dos visitas clínicas. [27]
La presión de cuña de la arteria pulmonar puede mostrar si hay insuficiencia cardíaca congestiva, trastornos de la válvula mitral y aórtica, hipervolemia , derivaciones o taponamiento cardíaco. [37]
Monitorización indirecta y remota del flujo sanguíneo mediante láser Doppler

La monitorización hemodinámica no invasiva de los vasos del fondo del ojo se puede realizar mediante holografía láser Doppler, con luz infrarroja cercana. El ojo ofrece una oportunidad única para la exploración no invasiva de enfermedades cardiovasculares . La obtención de imágenes láser Doppler mediante holografía digital puede medir el flujo sanguíneo en la retina y la coroides , cuyas respuestas Doppler exhiben un perfil en forma de pulso con el tiempo [38] [39] Esta técnica permite la microangiografía funcional no invasiva mediante la medición de alto contraste de las respuestas Doppler a partir de perfiles de flujo sanguíneo endoluminal en vasos del segmento posterior del ojo. Las diferencias en la presión arterial impulsan el flujo de sangre a lo largo de la circulación. La tasa de flujo sanguíneo medio depende tanto de la presión arterial como de la resistencia hemodinámica al flujo presentada por los vasos sanguíneos.
Glosario
- ANH
- Hemodilución normovolémica aguda
- ANH y
- Número de unidades durante la ANH
- BL H
- Máxima pérdida de sangre posible cuando se utiliza ANH antes de que sea necesaria una transfusión de sangre homóloga
- BL yo
- Posible pérdida de sangre incremental con ANH. (BL H – BL s )
- BL y
- Pérdida máxima de sangre sin ANH antes de que se requiera una transfusión de sangre homóloga
- virus de Epstein-Barr (VEB)
- Volumen sanguíneo estimado (70 ml/kg)
- Hct
- El hematocrito siempre se expresa aquí como fracción
- Hola
- Hematocrito inicial
- Yo soy
- Hematocrito mínimo seguro
- PRBC
- Equivalente de glóbulos rojos concentrados ahorrado por ANH
- RCM
- Masa de glóbulos rojos.
- RCM- H
- Masa celular disponible para transfusión después de la anestesia nacional
- RCM yo
- Masa de glóbulos rojos ahorrada por ANH
- SBL
- Pérdida de sangre quirúrgica
Etimología y pronunciación
La palabra hemodinámica ( / ˌh iːm əd aɪ ˈn æm ɪ k s , - m oʊ - / [40] ) utiliza formas combinadas de hemo- ( que proviene del griego antiguo haima , que significa sangre) y dinámica , por lo tanto " la dinámica de la sangre ". La vocal de la sílaba hemo- se escribe de diversas formas según la variación ae/e .
Notas y referencias
- ^ ab Tortora, Gerard J.; Derrickson, Bryan (2012). "El sistema cardiovascular: la sangre". Principios de anatomía y fisiología (13.ª ed.). John Wiley & Sons. págs. 729–732. ISBN 978-0-470-56510-0.
- ^ Fieldman, Joel S.; Phong, Duong H.; Saint-Aubin, Yvan; Vinet, Luc (2007). "Reología". Biología y mecánica de los flujos sanguíneos, parte II: mecánica y aspectos médicos . Springer. págs. 119–123. ISBN 978-0-387-74848-1.
- ^ Rand, Peter (31 de mayo de 1963). "Sangre humana en condiciones normotérmicas e hipotérmicas" (PDF) . Journal of Applied Physiology . 19 : 117–122. doi :10.1152/jappl.1964.19.1.117. PMID 14104265. Consultado el 16 de septiembre de 2014 .[ enlace muerto permanente ]
- ^ Errill, Edward W. (octubre de 1969). "Reología de la sangre". Physiological Reviews . 49 (4): 863–888. doi :10.1152/physrev.1969.49.4.863. PMID 4898603.
En sangre normal, a niveles de velocidad de cizallamiento tales que la ecuación 15 es aplicable, es decir, flujo newtoniano, se ha demostrado que el coeficiente de temperatura de la viscosidad es idéntico al del agua en el rango de 10-37 °C.
- ^ Cinar, Yildirim; Senyol, A. Mete; Duman, Kamber (mayo de 2001). "Viscosidad sanguínea y presión arterial: papel de la temperatura y la hiperglucemia". American Journal of Hypertension . 14 (5): 433–438. doi : 10.1016/S0895-7061(00)01260-7 . PMID 11368464.
- ^ abc Caro, CG; Pedley, TJ; Schroter, RC; Seed, WA (1978). La mecánica de la circulación . Oxford University Press. págs. 3–60, 151–176. ISBN 978-0-19-263323-1.
- ^ Naqash, Imtiaz A.; Draboo, MA; Lone, Abdul Qayoom; Nengroo, Showkat H.; Kirmani, Altaf; Bhat, Abdul Rashid (2011). "Evaluación de la hemodilución normovolémica aguda y la autotransfusión en pacientes neuroquirúrgicos sometidos a escisión de meningioma intracraneal". Revista de anestesiología y farmacología clínica . 27 (1): 54–58. doi : 10.4103/0970-9185.76645 . ISSN: 0970-9185. PMC: 3146160. PMID : 21804707.
- ^ Saito, Chihiro; Kamei, Tetsuya; Kubota, Shoji; Yoshida, Kiyoshi; Hibiya, Makoto; Hashimoto, Shuji (diciembre de 2018). "Asociación de hemodilución primaria y cebado autólogo retrógrado con transfusión en cirugía cardíaca: análisis de la base de datos de casos de perfusión de la Sociedad Japonesa de Tecnología Extracorpórea en Medicina". The Journal of Extra-corporeal Technology . 50 (4): 231–236. doi :10.1051/ject/201850231. ISSN 0022-1058. PMC 6296452 . PMID 30581230.
- ^ "Eficacia de la hemodilución normovolémica aguda, medida en función de la pérdida de sangre". Revista de la Sociedad Americana de Anestesiólogos, Inc. Archivado desde el original el 29 de junio de 2012. Consultado el 5 de abril de 2011 .
- ^ ab Kaya, M.; Li, JK-J. (2001). "Hemodilución: modelado y aspectos clínicos". Hemodilución: modelado y aspectos clínicos . Vol. 1. IEEE. págs. 177–179. doi :10.1109/IEMBS.2001.1018881. ISBN 978-0-7803-7211-5.S2CID 73295413 .
- ^ Feldman, Jeffrey M.; Roth, Jonathan V.; Bjoraker, David G. (enero de 1995). "Maximum blood saving by acute Normovolemia hemodilution" (Ahorro máximo de sangre mediante hemodilución normovolémica aguda). Anesthesia & Analgesia (Anestesia y analgesia ) . 80 (1): 108–113. doi : 10.1097/00000539-199501000-00019 . PMID: 7802266. S2CID : 24131754. Archivado desde el original el 23 de febrero de 2022. Consultado el 5 de abril de 2011 .
- ^ ab Costanzo, Linda S. (2003). Fisiología . Serie de revisiones de la junta (3.ª ed.). Filadelfia: Lippincott Williams & Wilkins. págs. 73-113. ISBN 978-0781739191.
- ^ King, Jordan; Lowery, David R. (2022), "Fisiología, gasto cardíaco", StatPearls , Treasure Island (FL): StatPearls Publishing, PMID 29262215 , consultado el 16 de mayo de 2022
- ^ Nasoori, Alireza; Taghipour, Ali; Shahbazzadeh, Delavar; Aminirissehei, Abdolhossein; Moghaddam, Sharif (2014). "Evaluación del lugar del corazón y la longitud de la cola en Naja oxiana, Macrovipera lebetina y Montivipera latifii". Revista Asia Pacífico de Medicina Tropical . 7 : S137–S142. doi : 10.1016/S1995-7645(14)60220-0 . PMID 25312108.
- ^ Lillywhite, Harvey B.; Albert, James S.; Sheehy, Coleman M.; Seymour, Roger S. (2012). "Gravedad y evolución de la morfología cardiopulmonar en serpientes". Comparative Biochemistry and Physiology . 161 (2): 230–242. doi :10.1016/j.cbpa.2011.10.029. PMC 3242868 . PMID 22079804.
- ^ abc Munson BR, Young DF, Okiishi TH, Huebsch WW (2009). Fundamentos de mecánica de fluidos (sexta edición). Nueva Jersey: John Wiley &Sons, Inc. pág. 725. ISBN 978-0-470-26284-9.
- ^ Fung, Yuan-cheng; Zweifach, BW (1971). "Microcirculación: mecánica del flujo sanguíneo en los capilares". Revisión anual de mecánica de fluidos . 3 : 189–210. Código Bibliográfico :1971AnRFM...3..189F. doi :10.1146/annurev.fl.03.010171.001201.
- ^ Tortora, Gerard J.; Derrickson, Bryan (2012). "El sistema cardiovascular: vasos sanguíneos y hemodinámica". Principios de anatomía y fisiología (13.ª ed.). John Wiley & Sons. pág. 816. ISBN 978-0470-56510-0.
- ^ Stücker, M.; Bailer, V.; Reuther, T.; Hoffman, K.; Kellam, K.; Altmeyer, P. (1996). "Velocidad de las células sanguíneas capilares en capilares de la piel humana ubicados perpendicularmente a la superficie de la piel: medida mediante un nuevo anemómetro láser Doppler". Investigación microvascular . 52 (2): 188–192. doi :10.1006/mvre.1996.0054. PMID 8901447.
- ^ Tortora, Gerard J.; Derrickson, Bryan (2012). "El sistema cardiovascular: vasos sanguíneos y hemodinámica". Principles of Anatomy & Physiology (Análisis de flujo laminar) (13.ª ed.). John Wiley & Sons. pág. 817. ISBN 978-0470-56510-0.
- ^ Marieb, Elaine N.; Hoehn, Katja (2013). "El sistema cardiovascular: vasos sanguíneos". Anatomía y fisiología humanas (novena edición). Pearson Education. pág. 712. ISBN 978-0-321-74326-8.
- ^ ab GB Thurston, Viscosidad y viscoelasticidad de la sangre en tubos de diámetro pequeño, Microvasular Research 11, 133 146, 1976
- ^ Womersley JR (1955). "Método para el cálculo de la velocidad, la tasa de flujo y la resistencia viscosa en las arterias cuando se conoce el gradiente de presión". Journal of Physiology . 127 (3): 553–563. doi :10.1113/jphysiol.1955.sp005276. PMC 1365740 . PMID 14368548.
- ^ Sircar, Sabyasach (2008). Principios de fisiología médica . India: Vistasta Publishing. ISBN 978-1-58890-572-7.
- ^ abc Fung, Yuan-cheng (1997). Biomecánica: circulación . Nueva York: Springer. pág. 571. ISBN. 978-0-387-94384-8.
- ^ Rosenson RS, Wolff D, Green D, Boss AH, Kensey KR (febrero de 2004). "Aspirina. La aspirina no altera la viscosidad sanguínea nativa". J. Thromb. Haemost . 2 (2): 340–341. doi : 10.1111/j.1538-79333.2004.0615f.x . PMID 14996003.
- ^ ab Delong, Claire; Sharma, Sandeep (2022), "Fisiología, resistencia vascular periférica", StatPearls , Treasure Island (FL): StatPearls Publishing, PMID 30855892 , consultado el 16 de mayo de 2022
- ^ Naderi, Nasim (1 de enero de 2022), Maleki, Majid; Alizadehasl, Azin; Haghjoo, Majid (eds.), "Capítulo 11 - Estudio hemodinámico", Practical Cardiology (segunda edición) , Elsevier, págs. 201–216, ISBN 978-0-323-80915-3, consultado el 22 de mayo de 2022
- ^ Potters (13 de febrero de 2014). "Medición de la tensión de corte de la pared mediante resonancia magnética con codificación de velocidad". Current Cardiovascular Imaging Reports . 7 (4). doi :10.1007/s12410-014-9257-1. S2CID 55721300.
- ^ Tazraei, P.; Riasi, A.; Takabi, B. (2015). "La influencia de las propiedades no newtonianas de la sangre en el golpe de sangre a través de la arteria cerebral posterior". Ciencias biológicas matemáticas . 264 : 119–127. doi :10.1016/j.mbs.2015.03.013. PMID 25865933.
- ^ Lough, Mary (15 de abril de 2015). Monitoreo hemodinámico: evolución de las tecnologías y la práctica clínica (1.ª ed.). St. Louis, Missouri: Elsevier Mosby. pág. 25. ISBN 978-0-323-08512-0.
- ^ ab Caro, Colin G. (1978). La mecánica de la circulación . Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-263323-1.
- ^ "Rango de presión arterial normal en adultos". Salud y Vida. 2010-06-07. Archivado desde el original el 2016-03-18 . Consultado el 2016-02-06 .
- ^ DeMers, Daniel; Wachs, Daliah (2022), "Fisiología, presión arterial media", StatPearls , Treasure Island (FL): StatPearls Publishing, PMID 30855814 , consultado el 22 de mayo de 2022
- ^ Klabunde, Richard (2005). Conceptos de fisiología cardiovascular . Lippincott Williams & Wilkins. págs. 93-94. ISBN. 978-0-7817-5030-1.
- ^ ab Markham LW, Knecht SK, Daniels SR, Mays WA, Khoury PR, Knilans TK (noviembre de 2004). "Desarrollo del gradiente de presión arterial brazo-pierna inducido por el ejercicio y compliancia arterial anormal en pacientes con coartación de aorta reparada". Am. J. Cardiol . 94 (9): 1200–1202. doi :10.1016/j.amjcard.2004.07.097. PMID 15518624.
- ^ "RHC | Centro Médico de la Universidad de Vanderbilt". medsites.vumc.org . Consultado el 16 de mayo de 2022 .
- ^ Puyo, L., M. Paques, M. Fink, JA. Sahel y M. Atlan. "Holografía láser Doppler in vivo de la retina humana". Biomedical optics express 9, no. 9 (2018): 4113-4129.
- ^ Puyo, Léo, Michel Paques, Mathias Fink, José-Alain Sahel y Michael Atlan. "Análisis de la forma de onda del flujo sanguíneo coroidal y retiniano humano con holografía láser Doppler". Biomedical Optics Express 10, n.º 10 (2019): 4942-4963.
- ^ "hemodinámica". Diccionario de inglés Lexico UK . Oxford University Press . Archivado desde el original el 22 de marzo de 2020.
Bibliografía
- Berne RM, Levy MN. Fisiología cardiovascular. Séptima edición, Mosby, 1997
- Rowell LB. Control cardiovascular humano. Oxford University Press 1993
- Braunwald E (Editor). Enfermedades cardíacas: un libro de texto de medicina cardiovascular. 5.ª edición. WBSaunders 1997
- Siderman S, Beyar R, Kleber AG. Electrofisiología cardíaca, circulación y transporte. Kluwer Academic Publishers 1991
- Asociación Estadounidense del Corazón
- Otto CM, Stoddard M, Waggoner A, Zoghbi WA. Recomendaciones para la cuantificación de la ecocardiografía Doppler: un informe del grupo de trabajo de cuantificación Doppler del Comité de nomenclatura y estándares de la Sociedad Estadounidense de Ecocardiografía. J Am Soc Echocardiogr 2002;15:167-184
- Peterson LH, La dinámica del flujo sanguíneo pulsátil, Circ. Res. 1954;2;127-139
- Monitorización hemodinámica, Bigatello LM, George E., Minerva Anestesiol, abril de 2002;68(4):219-25
- Claude Franceschi L'investigation vasculaire par ultrasonographie Doppler Masson 1979 ISBN Nr. 2-225-63679-6
- Claude Franceschi; Paolo Zamboni Principios de hemodinámica venosa Nova Science Publishers 2009-01 ISBN Nr. 1606924850/9781606924853
- Claude Franceschi Insuficiencia venosa de la pelvis y de las extremidades inferiores: Fundamento hemodinámico
- WR Milnor: Hemodinámica, Williams & Wilkins, 1982
- B Bo Sramek: Hemodinámica sistémica y manejo hemodinámico, 4.ª edición, ESBN 1-59196-046-0
Enlaces externos
- Aprenda hemodinámica

![{\displaystyle \ Q=K([P_{c}-P_{i}]S-[P_{c}-P_{i}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e42f7529864cb1070a1a07048e10d7e06fb125f1)
























