Espacio de fases
| Ecuaciones diferenciales |
|---|
| Alcance |
| Clasificación |
| Solución |
| People |
El espacio de fases de un sistema físico es el conjunto de todos los estados físicos posibles del sistema cuando se describe mediante una parametrización dada. Cada estado posible corresponde de forma única a un punto en el espacio de fases. Para los sistemas mecánicos , el espacio de fases suele estar formado por todos los valores posibles de los parámetros de posición y momento . Es el producto directo del espacio directo y el espacio recíproco . [ aclaración necesaria ] El concepto de espacio de fases fue desarrollado a finales del siglo XIX por Ludwig Boltzmann , Henri Poincaré y Josiah Willard Gibbs . [1]
Principios
En un espacio de fases, cada grado de libertad o parámetro del sistema se representa como un eje de un espacio multidimensional; un sistema unidimensional se denomina línea de fases , mientras que un sistema bidimensional se denomina plano de fases . Para cada estado posible del sistema o combinación permitida de valores de los parámetros del sistema, se incluye un punto en el espacio multidimensional. El estado evolutivo del sistema a lo largo del tiempo traza un camino (una trayectoria del espacio de fases para el sistema) a través del espacio de alta dimensión. La trayectoria del espacio de fases representa el conjunto de estados compatibles con el inicio desde una condición inicial particular , ubicada en el espacio de fases completo que representa el conjunto de estados compatibles con el inicio desde cualquier condición inicial. En su conjunto, el diagrama de fases representa todo lo que puede ser el sistema, y su forma puede dilucidar fácilmente cualidades del sistema que podrían no ser obvias de otra manera. Un espacio de fases puede contener una gran cantidad de dimensiones. Por ejemplo, un gas que contiene muchas moléculas puede requerir una dimensión separada para las posiciones x , y y z y los momentos de cada partícula (6 dimensiones para un gas monoatómico idealizado), y para sistemas moleculares más complejos se requieren dimensiones adicionales para describir los modos vibracionales de los enlaces moleculares, así como el giro alrededor de 3 ejes. Los espacios de fase son más fáciles de usar cuando se analiza el comportamiento de sistemas mecánicos restringidos al movimiento alrededor y a lo largo de varios ejes de rotación o traslación, por ejemplo, en robótica, como analizar el rango de movimiento de un brazo robótico o determinar la ruta óptima para lograr un resultado de posición/momento particular.

Momentos conjugados
En mecánica clásica, cualquier elección de coordenadas generalizadas q i para la posición (es decir, coordenadas en el espacio de configuración ) define momentos generalizados conjugados p i , que juntos definen coordenadas en el espacio de fases. De manera más abstracta, en mecánica clásica el espacio de fases es el fibrado cotangente del espacio de configuración, y en esta interpretación el procedimiento anterior expresa que una elección de coordenadas locales en el espacio de configuración induce una elección de coordenadas Darboux locales naturales para la estructura simpléctica estándar en un espacio cotangente.
Conjuntos estadísticos en el espacio de fases
El movimiento de un conjunto de sistemas en este espacio es estudiado por la mecánica estadística clásica . La densidad local de puntos en tales sistemas obedece al teorema de Liouville , y por lo tanto puede tomarse como constante. Dentro del contexto de un sistema modelo en mecánica clásica, las coordenadas del espacio de fases del sistema en un momento dado están compuestas por todas las variables dinámicas del sistema. Debido a esto, es posible calcular el estado del sistema en un momento dado en el futuro o en el pasado, a través de la integración de las ecuaciones de movimiento de Hamilton o de Lagrange.
En bajas dimensiones
En el caso de sistemas simples, puede haber tan solo uno o dos grados de libertad. Un grado de libertad se da cuando se tiene una ecuación diferencial ordinaria autónoma en una sola variable, y el sistema unidimensional resultante se denomina línea de fase , y el comportamiento cualitativo del sistema es inmediatamente visible desde la línea de fase. Los ejemplos no triviales más simples son el modelo de crecimiento exponencial /decaimiento (un equilibrio inestable/estable) y el modelo de crecimiento logístico (dos equilibrios, uno estable, uno inestable).
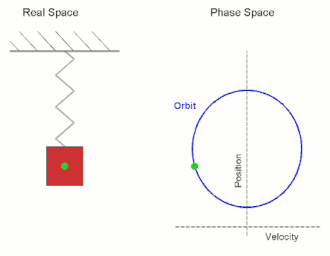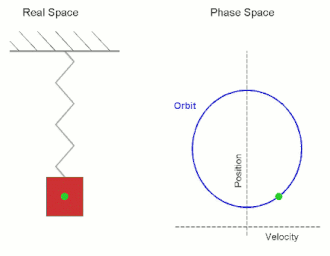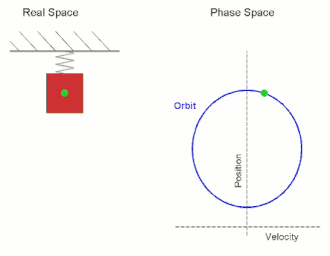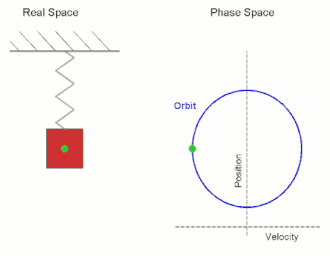
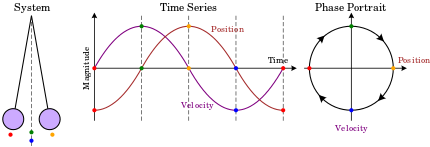
El espacio de fases de un sistema bidimensional se denomina plano de fases , que se da en la mecánica clásica para una sola partícula que se mueve en una dimensión, y donde las dos variables son la posición y la velocidad. En este caso, un esbozo del retrato de fases puede dar información cualitativa sobre la dinámica del sistema, como el ciclo límite del oscilador de Van der Pol que se muestra en el diagrama.
Aquí el eje horizontal indica la posición y el eje vertical la velocidad. A medida que el sistema evoluciona, su estado sigue una de las líneas (trayectorias) del diagrama de fases.

Conceptos relacionados
Diagrama de fases
Un gráfico de las variables de posición y momento en función del tiempo se denomina a veces gráfico de fases o diagrama de fases . Sin embargo, la última expresión, " diagrama de fases ", se reserva más habitualmente en las ciencias físicas para un diagrama que muestra las distintas regiones de estabilidad de las fases termodinámicas de un sistema químico, que consta de presión , temperatura y composición.
Retrato de fase


En matemáticas , un retrato de fase es una representación geométrica de las órbitas de un sistema dinámico en el plano de fase . Cada conjunto de condiciones iniciales está representado por un punto o curva diferente .
Los retratos de fase son una herramienta invaluable para estudiar sistemas dinámicos. Consisten en un gráfico de trayectorias típicas en el espacio de fases. Esto revela información como si existe un atractor , un repelente o un ciclo límite para el valor del parámetro elegido. El concepto de equivalencia topológica es importante para clasificar el comportamiento de los sistemas, ya que especifica cuándo dos retratos de fase diferentes representan el mismo comportamiento dinámico cualitativo. Un atractor es un punto estable que también se denomina "sumidero". El repelente se considera un punto inestable, que también se conoce como "fuente".
Un gráfico de retrato de fase de un sistema dinámico representa las trayectorias del sistema (con flechas) y los estados estables (con puntos) e inestables (con círculos) en un espacio de fases. Los ejes son de variables de estado .Integral de fase
En la mecánica estadística clásica (energías continuas), el concepto de espacio de fases proporciona un análogo clásico a la función de partición (suma de estados) conocida como integral de fase. [2] En lugar de sumar el factor de Boltzmann sobre estados de energía discretamente espaciados (definidos por números cuánticos enteros apropiados para cada grado de libertad), se puede integrar sobre el espacio de fases continuo. Dicha integración consta esencialmente de dos partes: la integración del componente de momento de todos los grados de libertad (espacio de momento) y la integración del componente de posición de todos los grados de libertad (espacio de configuración). Una vez que se conoce la integral de fase, se puede relacionar con la función de partición clásica mediante la multiplicación de una constante de normalización que representa el número de estados de energía cuántica por unidad de espacio de fases. Esta constante de normalización es simplemente la inversa de la constante de Planck elevada a una potencia igual al número de grados de libertad del sistema. [3]
Aplicaciones

Teoría del caos
Ejemplos clásicos de diagramas de fases de la teoría del caos son:
- El atractor de Lorenz
- crecimiento de la población (es decir, mapa logístico )
- plano de parámetros de polinomios cuadráticos complejos con conjunto de Mandelbrot .
Mecánica cuántica
En mecánica cuántica , las coordenadas p y q del espacio de fases normalmente se convierten en operadores hermíticos en un espacio de Hilbert .
Pero alternativamente pueden conservar su interpretación clásica, siempre que sus funciones se compongan de formas algebraicas novedosas (a través del producto estrella de Groenewold de 1946 ). Esto es consistente con el principio de incertidumbre de la mecánica cuántica. Cada observable mecánico cuántico corresponde a una función o distribución única en el espacio de fases, y a la inversa, como lo especificaron Hermann Weyl (1927) y complementaron John von Neumann (1931); Eugene Wigner (1932); y, en una gran síntesis, H. J. Groenewold (1946). Con J. E. Moyal (1949), estos completaron los fundamentos de la formulación del espacio de fases de la mecánica cuántica , una reformulación completa y lógicamente autónoma de la mecánica cuántica. [4] (Sus abstracciones modernas incluyen la cuantificación de la deformación y la cuantificación geométrica ).
Los valores esperados en la cuantificación del espacio de fase se obtienen de forma isomórfica a los observables del operador de seguimiento con la matriz de densidad en el espacio de Hilbert: se obtienen mediante integrales del espacio de fase de los observables, donde la distribución de cuasi-probabilidad de Wigner sirve efectivamente como medida.
Así, al expresar la mecánica cuántica en el espacio de fases (el mismo ámbito que para la mecánica clásica), el mapa de Weyl facilita el reconocimiento de la mecánica cuántica como una deformación (generalización) de la mecánica clásica, con parámetro de deformación ħ / S , donde S es la acción del proceso relevante. (Otras deformaciones familiares en física involucran la deformación de la mecánica clásica newtoniana en la mecánica relativista , con parámetro de deformación v / c ; [ cita requerida ] o la deformación de la gravedad newtoniana en la relatividad general , con parámetro de deformación radio de Schwarzschild /dimensión característica.) [ cita requerida ]
Las expresiones clásicas, los observables y las operaciones (como los corchetes de Poisson ) se modifican mediante correcciones cuánticas dependientes de ħ , ya que la multiplicación conmutativa convencional que se aplica en la mecánica clásica se generaliza a la multiplicación en estrella no conmutativa que caracteriza a la mecánica cuántica y subyace a su principio de incertidumbre.
Termodinámica y mecánica estadística
En los contextos de la termodinámica y la mecánica estadística , el término "espacio de fases" tiene dos significados: por un lado, se utiliza en el mismo sentido que en la mecánica clásica. Si un sistema termodinámico consta de N partículas, entonces un punto en el espacio de fases de 6 N dimensiones describe el estado dinámico de cada partícula en ese sistema, ya que cada partícula está asociada con 3 variables de posición y 3 variables de momento. En este sentido, siempre que las partículas sean distinguibles , se dice que un punto en el espacio de fases es un microestado del sistema. (Para partículas indistinguibles, un microestado consiste en un conjunto de N puntos, correspondientes a todos los posibles intercambios de las N partículas). N suele estar en el orden del número de Avogadro , por lo que describir el sistema a nivel microscópico a menudo es poco práctico. Esto conduce al uso del espacio de fases en un sentido diferente.
El espacio de fases también puede referirse al espacio parametrizado por los estados macroscópicos del sistema, como la presión, la temperatura, etc. Por ejemplo, se puede considerar que el diagrama de presión-volumen o el diagrama de temperatura-entropía describen parte de este espacio de fases. Un punto en este espacio de fases se denomina, en consecuencia, macroestado. Puede haber fácilmente más de un microestado con el mismo macroestado. Por ejemplo, para una temperatura fija, el sistema podría tener muchas configuraciones dinámicas a nivel microscópico. Cuando se utiliza en este sentido, una fase es una región del espacio de fases donde el sistema en cuestión se encuentra, por ejemplo, en la fase líquida o sólida , etc.
Como hay muchos más microestados que macroestados, el espacio de fases en el primer sentido suele ser una variedad de dimensiones mucho mayores que en el segundo sentido. Es evidente que se requieren muchos más parámetros para registrar cada detalle del sistema hasta la escala molecular o atómica que para especificar simplemente, por ejemplo, la temperatura o la presión del sistema.
Óptica
El espacio de fases se utiliza ampliamente en la óptica no generadora de imágenes , [5] la rama de la óptica dedicada a la iluminación. También es un concepto importante en la óptica hamiltoniana .
Medicamento
En medicina y bioingeniería , el método del espacio de fases se utiliza para visualizar respuestas fisiológicas multidimensionales . [6] [7]
Véase también
- Espacio de configuración (matemáticas)
- Minisuperespacio
- Línea de fase , caso unidimensional
- Plano de fase , caso bidimensional
- Retrato de fase
- Método del espacio de fases
- Espacio de parámetros
- Separatriz
- Aplicaciones
- Espacio de fase óptica
- Espacio de estados (controles) para obtener información sobre el espacio de estados (similar al estado de fase) en la ingeniería de control.
- Espacio de estados para obtener información sobre el espacio de estados con estados discretos en informática.
- Dinámica molecular
- Matemáticas
- Física
- Mecánica clásica
- Mecánica hamiltoniana
- Mecánica lagrangiana
- Espacio de estados (física) para obtener información sobre el espacio de estados en física
- Formulación del espacio de fases de la mecánica cuántica
- Características del espacio de fases de la mecánica cuántica
Referencias
- ^ Nolte, DD (2010). "La enredada historia del espacio de fases". Physics Today . 63 (4): 33–38. Bibcode :2010PhT....63d..33N. doi :10.1063/1.3397041. S2CID 17205307.
- ^ Laurendeau, Normand M. (2005). Termodinámica estadística: fundamentos y aplicaciones . Nueva York: Cambridge University Press. ISBN 0-521-84635-8.
- ^ Vu-Quoc, L. (2008). «Configuración integral». Archivado desde el original el 28 de abril de 2012.
- ^ Curtright, TL; Zachos, CK (2012). "Mecánica cuántica en el espacio de fases". Boletín de Física de Asia Pacífico . 01 : 37–46. arXiv : 1104.5269 . doi :10.1142/S2251158X12000069. S2CID 119230734.
- ^ Chaves, Julio (2015). Introducción a la óptica sin imágenes, segunda edición. CRC Press . ISBN 978-1482206739.
- ^ Klabukov, yo; Tenchurin, T.; Shepelev, A.; Baranovskii, D.; Mamagulashvili, V.; Dyuzheva, T.; Krasilnikova, O.; Balyasin, M.; Lyndup, A.; Krasheninnikov, M.; Sulina, Y.; Gomzyak, V.; Krasheninnikov, S.; Buzin, A.; Zayratyants, G. (2023). "Comportamientos biomecánicos y propiedades de degradación de andamios de polímeros multicapa: el método del espacio de fases para el diseño de vías biliares y la bioingeniería". Biomedicinas . 11 (3): 745. doi : 10.3390/biomedicinas11030745 . ISSN 2227-9059. PMC 10044742 . PMID 36979723.
- ^ Kirkland, MA (2004). "Un modelo de espacio de fases de la hematopoyesis y el concepto de renovación de células madre". Hematología experimental . 32 (6): 511–519. doi : 10.1016/j.exphem.2004.02.013 . hdl : 10536/DRO/DU:30101092 . ISSN 0301-472X. PMID 15183891.
Lectura adicional
- Nolte, DD (2015). Introducción a la dinámica moderna: caos, redes, espacio y tiempo . Oxford University Press. ISBN 978-0-19-965703-2.
- Nolte, DD (2018). Galileo sin límites: un camino a través de la vida, el universo y todo lo demás . Oxford University Press. ISBN 978-0-19-880584-7.
Enlaces externos
- "Espacio de fases", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]

