Efecto Doppler

El efecto Doppler (también llamado desplazamiento Doppler ) es el cambio en la frecuencia de una onda en relación con un observador que se mueve en relación con la fuente de la onda. ^{[1] [2] [3]} El efecto Doppler recibe su nombre del físico Christian Doppler , quien describió el fenómeno en 1842. Un ejemplo común de desplazamiento Doppler es el cambio de tono que se escucha cuando un vehículo que hace sonar la bocina se acerca y se aleja de un observador. En comparación con la frecuencia emitida, la frecuencia recibida es más alta durante la aproximación, idéntica en el instante de pasar y más baja durante la alejamiento. ^[4]

Cuando la fuente de la onda sonora se mueve hacia el observador, cada ciclo sucesivo de la onda se emite desde una posición más cercana al observador que el ciclo anterior. ^{[4] [5]} Por lo tanto, desde la perspectiva del observador, el tiempo entre ciclos se reduce, lo que significa que la frecuencia aumenta. Por el contrario, si la fuente de la onda sonora se aleja del observador, cada ciclo de la onda se emite desde una posición más alejada del observador que el ciclo anterior, por lo que el tiempo de llegada entre ciclos sucesivos aumenta, reduciendo así la frecuencia.

En el caso de las ondas que se propagan en un medio, como las ondas sonoras , la velocidad del observador y de la fuente son relativas al medio en el que se transmiten las ondas. ^[3] Por lo tanto, en tales casos, el efecto Doppler total puede resultar del movimiento de la fuente, del movimiento del observador, del movimiento del medio o de cualquier combinación de ellos. En el caso de las ondas que se propagan en el vacío , como es posible en el caso de las ondas electromagnéticas o las ondas gravitacionales , solo es necesario considerar la diferencia de velocidad entre el observador y la fuente.

Doppler propuso por primera vez este efecto en 1842 en su tratado " Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels " (Sobre la luz coloreada de las estrellas binarias y algunas otras estrellas del cielo). ^[6] La hipótesis fue probada para ondas sonoras por Buys Ballot en 1845. ^{[p 1]} Confirmó que el tono del sonido era más alto que la frecuencia emitida cuando la fuente de sonido se acercaba a él, y más bajo que la frecuencia emitida cuando la fuente de sonido se alejaba de él. Hippolyte Fizeau descubrió de forma independiente el mismo fenómeno en ondas electromagnéticas en 1848 (en Francia, el efecto a veces se llama "effet Doppler-Fizeau", pero ese nombre no fue adoptado por el resto del mundo ya que el descubrimiento de Fizeau fue seis años después de la propuesta de Doppler). ^{[p 2] [7]} En Gran Bretaña, John Scott Russell realizó un estudio experimental del efecto Doppler (1848). ^{[pág. 3]}

En la física clásica, donde las velocidades de la fuente y del receptor en relación con el medio son menores que la velocidad de las ondas en el medio, la relación entre la frecuencia observada y la frecuencia emitida viene dada por: ^[8] donde${\displaystyle f}$${\displaystyle f_{\text{0}}}$$${\displaystyle f=\left({\frac {c\pm v_{\text{r}}}{c\mp v_{\text{s}}}}\right)f_{0}}$$

• ${\displaystyle c}$es la velocidad de propagación de las ondas en el medio;
• ${\displaystyle v_{\text{r}}}$es la velocidad del receptor con respecto al medio. En la fórmula, se suma si el receptor se mueve hacia la fuente, se resta si el receptor se aleja de la fuente;${\displaystyle v_{\text{r}}}$${\displaystyle c}$
• ${\displaystyle v_{\text{s}}}$es la velocidad de la fuente con respecto al medio. se resta si la fuente se mueve hacia el receptor y se suma si la fuente se aleja del receptor.${\displaystyle v_{\text{s}}}$${\displaystyle c}$

Tenga en cuenta que esta relación predice que la frecuencia disminuirá si la fuente o el receptor se alejan el uno del otro.

De manera equivalente, bajo el supuesto de que la fuente se está acercando o alejando directamente del observador: donde $${\displaystyle {\frac {f}{v_{wr}}}={\frac {f_{0}}{v_{ws}}}={\frac {1}{\lambda }}}$$

• ${\displaystyle v_{wr}}$es la velocidad de la onda relativa al receptor;
• ${\displaystyle v_{ws}}$es la velocidad de la onda relativa a la fuente;
• ${\displaystyle \lambda }$es la longitud de onda.

Si la fuente se acerca al observador en un ángulo (pero con una velocidad constante), la frecuencia observada que se escucha primero es más alta que la frecuencia emitida por el objeto. A partir de entonces, hay una disminución monótona en la frecuencia observada a medida que se acerca al observador, a través de la igualdad cuando proviene de una dirección perpendicular al movimiento relativo (y se emitió en el punto de aproximación más cercano; pero cuando se recibe la onda, la fuente y el observador ya no estarán en su punto más cercano), y una disminución monótona continua a medida que se aleja del observador. Cuando el observador está muy cerca de la trayectoria del objeto, la transición de alta a baja frecuencia es muy abrupta. Cuando el observador está lejos de la trayectoria del objeto, la transición de alta a baja frecuencia es gradual.

Si las velocidades y son pequeñas en comparación con la velocidad de la onda, la relación entre la frecuencia observada y la frecuencia emitida es aproximadamente ^[8]${\displaystyle v_{\text{s}}}$${\displaystyle v_{\text{r}}\,}$${\displaystyle f}$${\displaystyle f_{\text{0}}}$

Frecuencia observada	Cambio de frecuencia
${\displaystyle f=\left(1+{\frac {\Delta v}{c}}\right)f_{0}}$	${\displaystyle \Delta f={\frac {\Delta v}{c}}f_{0}}$

dónde

• ${\displaystyle \Delta f=f-f_{0}}$
• ${\displaystyle \Delta v=-(v_{\text{r}}-v_{\text{s}})}$es el opuesto de la velocidad relativa del receptor con respecto a la fuente: es positiva cuando la fuente y el receptor se mueven uno hacia el otro.

• 
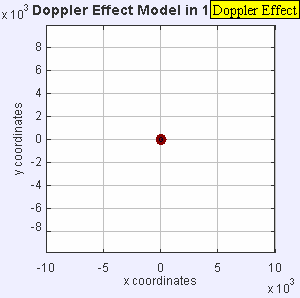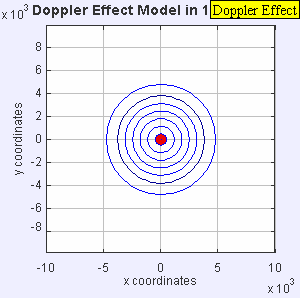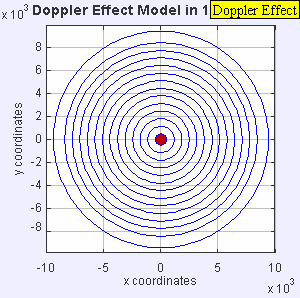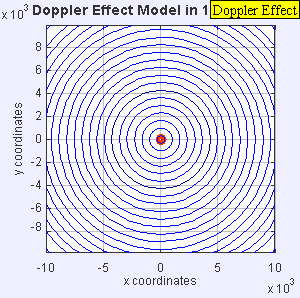
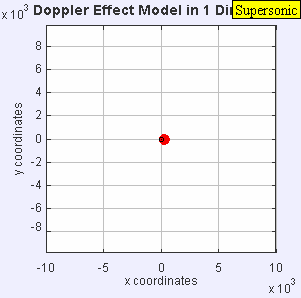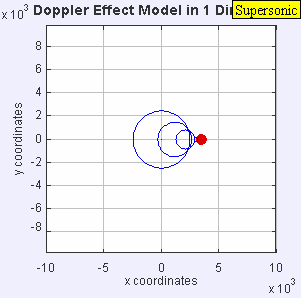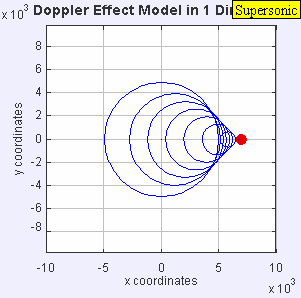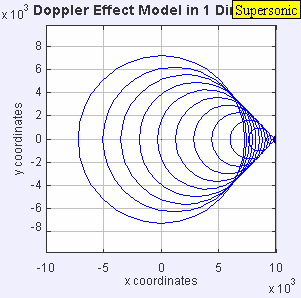
  Una fuente de sonido estacionaria produce ondas sonoras a una frecuencia constante f , y los frentes de onda se propagan simétricamente alejándose de la fuente a una velocidad constante c. La distancia entre los frentes de onda es la longitud de onda. Todos los observadores oirán la misma frecuencia, que será igual a la frecuencia real de la fuente donde f = f ₀ .
• 
  La misma fuente de sonido está emitiendo ondas sonoras a una frecuencia constante en el mismo medio. Sin embargo, ahora la fuente de sonido se está moviendo con una velocidad υ _s = 0,7 c . Como la fuente se está moviendo, el centro de cada nuevo frente de onda ahora está ligeramente desplazado hacia la derecha. Como resultado, los frentes de onda comienzan a agruparse en el lado derecho (delante) y se separan más en el lado izquierdo (detrás) de la fuente. Un observador frente a la fuente oirá una frecuencia más alta f = ⁠c + 0/c – 0,7 c⁠ f ₀ = 3,33 f ₀ y un observador detrás de la fuente oirá una frecuencia más baja f = ⁠c -0/c + 0,7 c⁠ f ₀ = 0,59 f ₀ .
• 
  Ahora la fuente se mueve a la velocidad del sonido en el medio ( υ _s = c ). Los frentes de onda que se encuentran frente a la fuente ahora están todos agrupados en el mismo punto. Como resultado, un observador que se encuentre frente a la fuente no detectará nada hasta que llegue la fuente y un observador que se encuentre detrás de la fuente oirá una frecuencia más baja f = ⁠c -0/c + c⁠ f ₀ = 0,5 f ₀ .
• 
  La fuente de sonido ya ha superado la velocidad del sonido en el medio y viaja a 1,4 c . Como la fuente se mueve más rápido que las ondas sonoras que crea, en realidad lidera el frente de onda que avanza. La fuente de sonido pasará por un observador estacionario antes de que este escuche el sonido. Como resultado, un observador frente a la fuente no detectará nada y un observador detrás de la fuente escuchará una frecuencia más baja f = ⁠c -0/c + 1,4 c⁠ f ₀ = 0,42 f ₀ .

Suponiendo un observador estacionario y una fuente de ondas que se mueve hacia el observador a (o excediendo) la velocidad de la onda, la ecuación Doppler predice una frecuencia infinita (o negativa) desde la perspectiva del observador. Por lo tanto, la ecuación Doppler no es aplicable para tales casos. Si la onda es una onda sonora y la fuente sonora se mueve más rápido que la velocidad del sonido, la onda de choque resultante crea un estampido sónico .

Lord Rayleigh predijo el siguiente efecto en su clásico libro sobre el sonido: si el observador se moviera de la fuente (estacionaria) al doble de la velocidad del sonido, una pieza musical previamente emitida por esa fuente se oiría con el tempo y tono correctos, pero como si se tocara al revés . ^[9]

La sirena de un vehículo de emergencia que pasa en movimiento suena más alta que su tono estacionario, se va reduciendo a medida que pasa y continúa sonando más baja que su tono estacionario a medida que se aleja del observador. El astrónomo John Dobson explicó el efecto de esta manera:

La razón por la que la sirena se desliza es porque no te golpea.

En otras palabras, si la sirena se acercara directamente al observador, el tono permanecería constante, en un tono más alto que el estacionario, hasta que el vehículo lo golpeara, y luego saltaría inmediatamente a un nuevo tono más bajo. Debido a que el vehículo pasa por el observador, la velocidad radial no permanece constante, sino que varía en función del ángulo entre su línea de visión y la velocidad de la sirena: donde es el ángulo entre la velocidad hacia adelante del objeto y la línea de visión desde el objeto hasta el observador.$${\displaystyle v_{\text{radial}}=v_{\text{s}}\cos(\theta )}$$${\displaystyle \theta }$

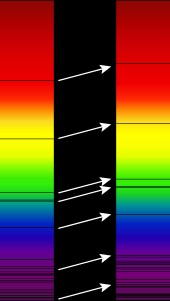
El efecto Doppler para ondas electromagnéticas como la luz es de uso generalizado en astronomía para medir la velocidad a la que las estrellas y galaxias se acercan o se alejan de nosotros, lo que resulta en el llamado corrimiento al azul o corrimiento al rojo , respectivamente. Esto puede usarse para detectar si una estrella aparentemente única es, en realidad, un sistema binario cercano , para medir la velocidad de rotación de estrellas y galaxias, o para detectar exoplanetas . Este efecto generalmente ocurre en una escala muy pequeña; no habría una diferencia notable en la luz visible a simple vista. ^[10] El uso del efecto Doppler en astronomía depende del conocimiento de frecuencias precisas de líneas discretas en los espectros de las estrellas.

Entre las estrellas cercanas , las velocidades radiales más altas con respecto al Sol son +308 km/s (BD-15°4041, también conocida como LHS 52, a 81,7 años luz de distancia) y −260 km/s (Woolley 9722, también conocida como Wolf 1106 y LHS 64, a 78,2 años luz de distancia). La velocidad radial positiva significa que la estrella se está alejando del Sol, la negativa que se está acercando.

El corrimiento al rojo también se utiliza para medir la expansión del universo . A veces se afirma que no se trata realmente de un efecto Doppler, sino que surge de la expansión del espacio. ^[11] Sin embargo, esta imagen puede ser engañosa porque la expansión del espacio es solo una convención matemática, que corresponde a una elección de coordenadas . ^[12] La interpretación más natural del corrimiento al rojo cosmológico es que es, en efecto, un corrimiento Doppler. ^[13]

Las galaxias distantes también presentan movimientos peculiares que son distintos de sus velocidades de recesión cosmológica. Si se utilizan los desplazamientos al rojo para determinar las distancias de acuerdo con la ley de Hubble , estos movimientos peculiares dan lugar a distorsiones del espacio de desplazamiento al rojo . ^[14]

El efecto Doppler se utiliza en algunos tipos de radar para medir la velocidad de los objetos detectados. Se dispara un haz de radar a un objetivo en movimiento (por ejemplo, un automóvil, ya que la policía utiliza el radar para detectar a los automovilistas que van a exceso de velocidad) cuando se acerca o se aleja de la fuente del radar. Cada onda de radar sucesiva tiene que viajar más lejos para llegar al automóvil, antes de reflejarse y volver a detectarse cerca de la fuente. A medida que cada onda tiene que moverse más lejos, la brecha entre cada onda aumenta, lo que aumenta la longitud de onda. En algunas situaciones, el haz de radar se dispara al automóvil en movimiento cuando se acerca, en cuyo caso cada onda sucesiva viaja una distancia menor, lo que disminuye la longitud de onda. En cualquier situación, los cálculos del efecto Doppler determinan con precisión la velocidad del automóvil. Además, la espoleta de proximidad , desarrollada durante la Segunda Guerra Mundial, se basa en el radar Doppler para detonar explosivos en el momento, la altura, la distancia, etc. correctos. ^{[ cita requerida ]}

Debido a que el desplazamiento Doppler afecta la onda incidente sobre el objetivo así como la onda reflejada hacia el radar, el cambio en la frecuencia observado por un radar debido a un objetivo que se mueve a una velocidad relativa es el doble del que se produce cuando el mismo objetivo emite una onda: ^[15]${\displaystyle \Delta v}$$${\displaystyle \Delta f={\frac {2\Delta v}{c}}f_{0}.}$$

Un ecocardiograma puede, dentro de ciertos límites, producir una evaluación precisa de la dirección del flujo sanguíneo y la velocidad de la sangre y el tejido cardíaco en cualquier punto arbitrario utilizando el efecto Doppler. Una de las limitaciones es que el haz de ultrasonidos debe ser lo más paralelo posible al flujo sanguíneo. Las mediciones de velocidad permiten la evaluación de las áreas y la función de las válvulas cardíacas, las comunicaciones anormales entre el lado izquierdo y derecho del corazón, la fuga de sangre a través de las válvulas (regurgitación valvular) y el cálculo del gasto cardíaco . La ecografía mejorada con contraste utilizando medios de contraste de microburbujas llenas de gas se puede utilizar para mejorar la velocidad u otras mediciones médicas relacionadas con el flujo. ^{[16] [17]}

Aunque "Doppler" se ha convertido en sinónimo de "medición de velocidad" en imágenes médicas, en muchos casos no es el cambio de frecuencia (desplazamiento Doppler) de la señal recibida lo que se mide, sino el cambio de fase ( cuando llega la señal recibida). ^{[p 4]}

Las mediciones de la velocidad del flujo sanguíneo también se utilizan en otros campos de la ecografía médica , como la ecografía obstétrica y la neurología . La medición de la velocidad del flujo sanguíneo en arterias y venas basada en el efecto Doppler es una herramienta eficaz para el diagnóstico de problemas vasculares como la estenosis . ^[18]

Se han desarrollado instrumentos como el velocímetro láser Doppler (LDV) y el velocímetro acústico Doppler (ADV) para medir las velocidades en un flujo de fluido. El LDV emite un haz de luz y el ADV emite una ráfaga acústica ultrasónica y mide el desplazamiento Doppler en las longitudes de onda de las reflexiones de las partículas que se mueven con el flujo. El flujo real se calcula como una función de la velocidad y la fase del agua. Esta técnica permite realizar mediciones de flujo no intrusivas, con alta precisión y alta frecuencia.

Desarrollada originalmente para mediciones de velocidad en aplicaciones médicas (flujo sanguíneo), la velocimetría Doppler ultrasónica (UDV) puede medir en tiempo real el perfil completo de velocidad en casi cualquier líquido que contenga partículas en suspensión, como polvo, burbujas de gas o emulsiones. Los flujos pueden ser pulsantes, oscilantes, laminares o turbulentos, estacionarios o transitorios. Esta técnica es completamente no invasiva.

El efecto Doppler se puede aprovechar para la navegación por satélite , como en Transit y DORIS .

El efecto Doppler también debe compensarse en las comunicaciones por satélite . Los satélites que se mueven rápidamente pueden tener un efecto Doppler de decenas de kilohercios en relación con una estación terrestre. La velocidad, y por tanto la magnitud del efecto Doppler, cambia debido a la curvatura de la Tierra. La compensación Doppler dinámica, en la que la frecuencia de una señal cambia progresivamente durante la transmisión, se utiliza para que el satélite reciba una señal de frecuencia constante. ^[20] Después de darse cuenta de que el efecto Doppler no se había tenido en cuenta antes del lanzamiento de la sonda Huygens de la misión Cassini-Huygens de 2005 , se alteró la trayectoria de la sonda para acercarse a Titán de tal manera que sus transmisiones viajaran perpendiculares a su dirección de movimiento en relación con Cassini, lo que redujo en gran medida el efecto Doppler. ^[21]

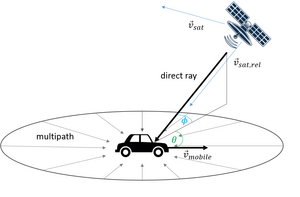
El desplazamiento Doppler de la trayectoria directa se puede estimar mediante la siguiente fórmula: ^[22] donde es la velocidad de la estación móvil, es la longitud de onda de la portadora, es el ángulo de elevación del satélite y es la dirección de conducción con respecto al satélite.$${\displaystyle f_{\rm {D,dir}}={\frac {v_{\rm {mob}}}{\lambda _{\rm {c}}}}\cos \phi \cos \theta }$$${\displaystyle v_{\text{mob}}}$${\displaystyle \lambda _{\rm {c}}}$${\displaystyle \phi }$${\displaystyle \theta }$

El desplazamiento Doppler adicional debido al movimiento del satélite se puede describir como: donde es la velocidad relativa del satélite.$${\displaystyle f_{\rm {D,sat}}={\frac {v_{\rm {rel,sat}}}{\lambda _{\rm {c}}}}}$$${\displaystyle v_{\rm {rel,sat}}}$

El altavoz Leslie , que se asocia más comúnmente con el famoso órgano Hammond y se utiliza predominantemente con él, aprovecha el efecto Doppler mediante el uso de un motor eléctrico para hacer girar una bocina acústica alrededor de un altavoz, enviando su sonido en un círculo. Esto da como resultado que en el oído del oyente se escuchen frecuencias de notas del teclado que fluctúan rápidamente.

Un vibrómetro láser Doppler (LDV) es un instrumento sin contacto para medir la vibración. El haz láser del LDV se dirige a la superficie de interés y la amplitud y frecuencia de la vibración se extraen del desplazamiento Doppler de la frecuencia del haz láser debido al movimiento de la superficie.

La planificación dinámica de rutas en tiempo real en robótica para ayudar al movimiento de robots en un entorno sofisticado con obstáculos móviles a menudo requiere la ayuda del efecto Doppler. ^[23] Estas aplicaciones se utilizan especialmente para la robótica competitiva donde el entorno cambia constantemente, como el robosoccer.

Desde 1968, científicos como Victor Veselago han especulado sobre la posibilidad de un efecto Doppler inverso. El tamaño del efecto Doppler depende del índice de refracción del medio por el que viaja una onda. Algunos materiales son capaces de refracción negativa , lo que debería conducir a un efecto Doppler que funciona en una dirección opuesta a la de un efecto Doppler convencional. ^[24] El primer experimento que detectó este efecto fue realizado por Nigel Seddon y Trevor Bearpark en Bristol , Reino Unido , en 2003. ^{[p 5]} Más tarde, el efecto Doppler inverso se observó en algunos materiales no homogéneos y se predijo dentro de un cono de Vavilov-Cherenkov. ^[25]

• Doppler, C. (1842). Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (Sobre la luz coloreada de las estrellas binarias y algunas otras estrellas del cielo) . Editorial: Abhandlungen der Königl. Bohm. Gesellschaft der Wissenschaften (V. Folge, Bd. 2, S. 465–482) [Actas de la Real Sociedad Bohemia de Ciencias (Parte V, Vol 2)]; Praga: 1842 (reeditado en 1903). Algunas fuentes mencionan 1843 como año de publicación porque en ese año se publicó el artículo en las Actas de la Sociedad Bohemia de Ciencias. El propio Doppler se refirió a la publicación como "Prag 1842 bei Borrosch und André", porque en 1842 hizo imprimir una edición preliminar que distribuyó de forma independiente.
• "Doppler y el efecto Doppler", EN da C. Andrade, Endeavour Vol. XVIII No. 69, enero de 1959 (publicado por ICI Londres). Relato histórico del artículo original de Doppler y desarrollos posteriores.
• David Nolte (2020). La caída y el ascenso del efecto Doppler. Physics Today, v. 73, págs. 31 - 35. DOI: 10.1063/PT.3.4429
• Adrian, Eleni (24 de junio de 1995). «Efecto Doppler». NCSA . Archivado desde el original el 12 de mayo de 2009. Consultado el 13 de julio de 2008 .

• Medios relacionados con el efecto Doppler en Wikimedia Commons
• El efecto Doppler - Las conferencias Feynman sobre física
• Efecto Doppler, ScienceWorld