Tensión (física)

La tensión es la fuerza de tracción o estiramiento transmitida axialmente a lo largo de un objeto, como una cuerda, una soga, una cadena, una varilla, un elemento de armadura u otro objeto, con el fin de estirarlo o separarlo. En términos de fuerza, es lo opuesto a la compresión . La tensión también se puede describir como el par de fuerzas de acción-reacción que actúan en cada extremo de un objeto.

A nivel atómico, cuando los átomos o las moléculas se separan entre sí y ganan energía potencial con una fuerza restauradora aún existente, la fuerza restauradora podría crear lo que también se llama tensión. Cada extremo de una cuerda o varilla bajo tal tensión podría tirar del objeto al que está unido, para restaurar la cuerda o varilla a su longitud relajada.

La tensión (como fuerza transmitida, como par de fuerzas acción-reacción o como fuerza restauradora) se mide en newtons en el Sistema Internacional de Unidades (o libras-fuerza en unidades imperiales ). Los extremos de una cuerda u otro objeto que transmite tensión ejercerán fuerzas sobre los objetos a los que está conectada la cuerda o varilla, en la dirección de la cuerda en el punto de unión. Estas fuerzas debidas a la tensión también se denominan "fuerzas pasivas". Hay dos posibilidades básicas para los sistemas de objetos sostenidos por cuerdas: ^[1] o bien la aceleración es cero y, por lo tanto, el sistema está en equilibrio, o bien hay aceleración y, por lo tanto, hay una fuerza neta presente en el sistema.

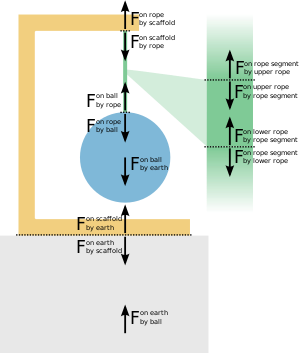
La tensión en una cuerda es una cantidad vectorial no negativa . La tensión cero es holgura. Una cuerda o soga a menudo se idealiza como unidimensional, con una longitud fija pero sin masa y con una sección transversal cero . Si no hay curvas en la cuerda, como ocurre con las vibraciones o las poleas , entonces la tensión es una constante a lo largo de la cuerda, igual a la magnitud de las fuerzas aplicadas por los extremos de la cuerda. Según la tercera ley de Newton , estas son las mismas fuerzas ejercidas sobre los extremos de la cuerda por los objetos a los que están unidos los extremos. Si la cuerda se curva alrededor de una o más poleas, seguirá teniendo una tensión constante a lo largo de su longitud en la situación idealizada de que las poleas no tengan masa ni fricción . Una cuerda vibrante vibra con un conjunto de frecuencias que dependen de la tensión de la cuerda. Estas frecuencias se pueden derivar de las leyes del movimiento de Newton . Cada segmento microscópico de la cuerda tira de sus segmentos vecinos y es tirado por ellos, con una fuerza igual a la tensión en esa posición a lo largo de la cuerda.

Si la cuerda tiene curvatura, entonces los dos tirones sobre un segmento por sus dos vecinos no sumarán cero, y habrá una fuerza neta sobre ese segmento de la cuerda, causando una aceleración. Esta fuerza neta es una fuerza restauradora , y el movimiento de la cuerda puede incluir ondas transversales que resuelven la ecuación central para la teoría de Sturm-Liouville : donde es la constante de fuerza por unidad de longitud [unidades de fuerza por área], es el ...., es el ...., y son los valores propios para resonancias de desplazamiento transversal en la cuerda, ^[2] con soluciones que incluyen los diversos armónicos en un instrumento de cuerda .$${\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}{\bigg [}\tau (x){\frac {\mathrm {d} \rho (x)}{\mathrm {d} x}}{\bigg ]}+v(x)\rho (x)=\omega ^{2}\sigma (x)\rho (x)}$$${\estilo de visualización v(x)}$${\displaystyle \sigma(x)}$${\displaystyle \tau(x)}$${\displaystyle \omega ^{2}}$${\displaystyle \rho(x)}$

La tensión también se utiliza para describir la fuerza ejercida por los extremos de un material tridimensional y continuo, como una varilla o un miembro de armadura . En este contexto, la tensión es análoga a la presión negativa . Una varilla bajo tensión se alarga . La cantidad de alargamiento y la carga que provocará la falla dependen de la fuerza por área de sección transversal en lugar de la fuerza sola, por lo que la tensión = fuerza axial / área de sección transversal es más útil para fines de ingeniería que la tensión. La tensión es una matriz de 3x3 llamada tensor , y el elemento del tensor de tensión es la fuerza de tracción por área, o fuerza de compresión por área, denotada como un número negativo para este elemento, si la varilla se comprime en lugar de alargarse.$estilo de visualización {\displaystyle \sigma _{11}}$

De esta manera, se puede obtener un escalar análogo a la tensión tomando la traza del tensor de tensión. ^[3]

Un sistema está en equilibrio cuando la suma de todas las fuerzas es cero. ^[1]$${\displaystyle \sum {\vec {F}}=0}$$

Por ejemplo, considere un sistema que consiste en un objeto que se baja verticalmente mediante una cuerda con tensión, T , a una velocidad constante . El sistema tiene una velocidad constante y, por lo tanto, está en equilibrio porque la tensión en la cuerda, que tira hacia arriba del objeto, es igual a la fuerza del peso , mg ("m" es la masa, "g" es la aceleración causada por la gravedad de la Tierra ), que tira del objeto hacia abajo. ^[1]$${\displaystyle \sum {\vec {F}}={\vec {T}}+m{\vec {g}}=0}$$

Un sistema tiene una fuerza neta cuando se ejerce sobre él una fuerza desequilibrada, es decir, la suma de todas las fuerzas no es cero. La aceleración y la fuerza neta siempre existen juntas. ^[1]$${\displaystyle \sum {\vec {F}}\neq 0}$$

Por ejemplo, considere el mismo sistema que el anterior pero suponga que el objeto ahora se baja con una velocidad creciente hacia abajo (aceleración positiva), por lo tanto, existe una fuerza neta en algún lugar del sistema. En este caso, la aceleración negativa indicaría que . ^[1]${\displaystyle |mg|>|T|}$$${\displaystyle \sum {\vec {F}}={\vec {T}}-m{\vec {g}}\neq 0}$$

En otro ejemplo, supongamos que dos cuerpos A y B que tienen masas y , respectivamente, están conectados entre sí por una cuerda inextensible sobre una polea sin fricción. Hay dos fuerzas que actúan sobre el cuerpo A: su peso ( ) tirando hacia abajo, y la tensión en la cuerda tirando hacia arriba. Por lo tanto, la fuerza neta sobre el cuerpo A es , por lo que . En una cuerda extensible, se aplica la ley de Hooke .$Estilo de visualización m_{1}$$Estilo de visualización m_{2}$${\displaystyle w_{1}=m_{1}g}$${\estilo de visualización T}$$Estilo de visualización F_{1}$$estilo de visualización w_{1}-T$${\displaystyle m_{1}a=m_{1}gT}$

Los objetos similares a cuerdas en las teorías relativistas , como las cuerdas utilizadas en algunos modelos de interacciones entre quarks o las utilizadas en la teoría de cuerdas moderna , también poseen tensión. Estas cuerdas se analizan en términos de su hoja de universo y, por lo tanto, la energía suele ser proporcional a la longitud de la cuerda. Como resultado, la tensión en dichas cuerdas es independiente de la cantidad de estiramiento.

Wikimedia Commons tiene medios relacionados con Tensión .

Wikiquote tiene citas relacionadas con Tensión .

• Mecánica de medios continuos
• Factor de caída
• Tensión superficial
• Resistencia a la tracción
• Tracción (mecánica)
• Presión hidrostática