Fusión nuclear
| Física nuclear |
|---|
 |
La fusión nuclear es una reacción en la que dos o más núcleos atómicos , generalmente deuterio y tritio ( isótopos de hidrógeno ), se combinan para formar uno o más núcleos atómicos diferentes y partículas subatómicas ( neutrones o protones ). La diferencia de masa entre los reactivos y los productos se manifiesta como liberación o absorción de energía . Esta diferencia de masa surge debido a la diferencia en la energía de enlace nuclear entre los núcleos atómicos antes y después de la reacción. La fusión nuclear es el proceso que alimenta a las estrellas activas o de secuencia principal y otras estrellas de gran magnitud , donde se liberan grandes cantidades de energía .
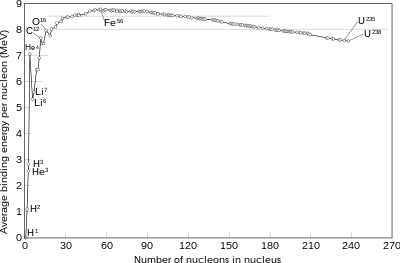
Un proceso de fusión nuclear que produce núcleos atómicos más ligeros que el hierro-56 o el níquel-62 generalmente liberará energía. Estos elementos tienen una masa relativamente pequeña y una energía de enlace relativamente grande por nucleón . La fusión de núcleos más ligeros que estos libera energía (un proceso exotérmico ), mientras que la fusión de núcleos más pesados da como resultado energía retenida por los nucleones del producto, y la reacción resultante es endotérmica . Lo opuesto es cierto para el proceso inverso, llamado fisión nuclear . La fusión nuclear utiliza elementos más ligeros, como el hidrógeno y el helio , que en general son más fusibles; mientras que los elementos más pesados, como el uranio , el torio y el plutonio , son más fisionables. El evento astrofísico extremo de una supernova puede producir suficiente energía para fusionar núcleos en elementos más pesados que el hierro.
Historia
El químico estadounidense William Draper Harkins fue el primero en proponer el concepto de fusión nuclear en 1915. [2] Luego, en 1921, Arthur Eddington sugirió que la fusión de hidrógeno y helio podría ser la fuente principal de energía estelar. [3] El efecto túnel cuántico fue descubierto por Friedrich Hund en 1927, [4] [5] y poco después Robert Atkinson y Fritz Houtermans utilizaron las masas medidas de elementos ligeros para demostrar que se podían liberar grandes cantidades de energía fusionando núcleos pequeños. [6] Basándose en los primeros experimentos de transmutación nuclear artificial de Patrick Blackett , Mark Oliphant logró la fusión de isótopos de hidrógeno en laboratorio en 1932. [7] En el resto de esa década, Hans Bethe elaboró la teoría del ciclo principal de fusión nuclear en las estrellas . La investigación sobre la fusión con fines militares comenzó a principios de la década de 1940 como parte del Proyecto Manhattan . La primera fusión nuclear exitosa se llevó a cabo el 1 de noviembre de 1952, en la prueba de la bomba de hidrógeno (termonuclear) Ivy Mike .
Si bien la fusión se logró con la bomba de hidrógeno (bomba H), la reacción debe ser controlada y sostenida para que sea una fuente de energía útil. La investigación para desarrollar la fusión controlada dentro de los reactores de fusión se ha llevado a cabo desde la década de 1930, pero la tecnología aún se encuentra en su fase de desarrollo. [8]
La Instalación Nacional de Ignición de Estados Unidos, que utiliza fusión por confinamiento inercial impulsada por láser , fue diseñada con el objetivo de lograr una fusión de equilibrio ; los primeros experimentos con objetivos láser a gran escala se realizaron en junio de 2009 y los experimentos de ignición comenzaron a principios de 2011. [9] [10] El 13 de diciembre de 2022, el Departamento de Energía de los Estados Unidos anunció que el 5 de diciembre de 2022 habían logrado con éxito la fusión de equilibrio, "entregando 2,05 megajulios (MJ) de energía al objetivo, lo que resultó en una salida de energía de fusión de 3,15 MJ". [11]
Antes de este gran avance, las reacciones de fusión controlada no habían sido capaces de producir una fusión controlada que alcanzara el punto de equilibrio (autosostenible). [12] Los dos enfoques más avanzados para ello son el confinamiento magnético (diseños toroidales) y el confinamiento inercial (diseños láser). Se están desarrollando diseños viables para un reactor toroidal que teóricamente proporcionará diez veces más energía de fusión que la cantidad necesaria para calentar el plasma a las temperaturas requeridas (véase ITER ). Se espera que la instalación ITER finalice su fase de construcción en 2025. Comenzará la puesta en servicio del reactor ese mismo año e iniciará los experimentos de plasma en 2025, pero no se espera que comience la fusión completa deuterio-tritio hasta 2035. [13]
Solo en 2021, las empresas privadas que buscan comercializar la fusión nuclear recibieron 2.600 millones de dólares en financiación privada, que se destinó a muchas empresas emergentes notables, entre ellas, Commonwealth Fusion Systems , Helion Energy Inc. , General Fusion , TAE Technologies Inc. y Zap Energy Inc. [14].
Uno de los avances más recientes hasta la fecha en el mantenimiento de una reacción de fusión sostenida se produjo en el reactor de fusión WEST de Francia, que mantuvo un plasma a 90 millones de grados durante un tiempo récord de seis minutos. Se trata de un reactor de tipo tokamak, el mismo estilo que el futuro reactor ITER. [15]
Proceso
La liberación de energía con la fusión de elementos ligeros se debe a la interacción de dos fuerzas opuestas: la fuerza nuclear , una manifestación de la interacción fuerte , que mantiene a los protones y neutrones fuertemente unidos en el núcleo atómico ; y la fuerza de Coulomb , que hace que los protones con carga positiva en el núcleo se repelan entre sí. [17] Los núcleos más ligeros (núcleos más pequeños que el hierro y el níquel) son suficientemente pequeños y pobres en protones para permitir que la fuerza nuclear supere la fuerza de Coulomb. Esto se debe a que el núcleo es suficientemente pequeño como para que todos los nucleones sientan la fuerza de atracción de corto alcance al menos tan fuertemente como sienten la repulsión de Coulomb de alcance infinito. La construcción de núcleos a partir de núcleos más ligeros por fusión libera la energía adicional de la atracción neta de partículas. Sin embargo, para núcleos más grandes , no se libera energía, porque la fuerza nuclear es de corto alcance y no puede actuar a través de núcleos más grandes.
La fusión alimenta a las estrellas y produce prácticamente todos los elementos en un proceso llamado nucleosíntesis . El Sol es una estrella de secuencia principal y, como tal, genera su energía mediante la fusión nuclear de núcleos de hidrógeno en helio. En su núcleo, el Sol fusiona 620 millones de toneladas métricas de hidrógeno y produce 616 millones de toneladas métricas de helio cada segundo. La fusión de elementos más ligeros en las estrellas libera energía y la masa que siempre la acompaña. Por ejemplo, en la fusión de dos núcleos de hidrógeno para formar helio, el 0,645% de la masa se elimina en forma de energía cinética de una partícula alfa u otras formas de energía, como la radiación electromagnética. [18]
Se necesita una energía considerable para obligar a los núcleos a fusionarse, incluso los del elemento más ligero, el hidrógeno . Cuando se aceleran a velocidades suficientemente altas, los núcleos pueden superar esta repulsión electrostática y acercarse lo suficiente como para que la fuerza nuclear atractiva sea mayor que la fuerza de repulsión de Coulomb. La fuerza fuerte crece rápidamente una vez que los núcleos están lo suficientemente cerca, y los nucleones que se fusionan pueden esencialmente "caer" unos sobre otros y el resultado es la fusión; este es un proceso exotérmico . [19]
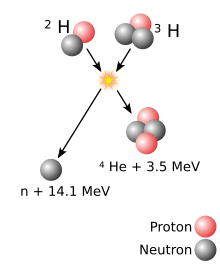
La energía liberada en la mayoría de las reacciones nucleares es mucho mayor que en las reacciones químicas , porque la energía de enlace que mantiene unido un núcleo es mayor que la energía que mantiene unidos a los electrones . Por ejemplo, la energía de ionización que se obtiene al agregar un electrón a un núcleo de hidrógeno es13,6 eV —menos de una millonésima parte de la17,6 MeV liberados en la reacción deuterio - tritio (D–T) que se muestra en el diagrama adyacente. Las reacciones de fusión tienen una densidad de energía muchas veces mayor que la fisión nuclear ; las reacciones producen mucha más energía por unidad de masa, aunque las reacciones de fisión individuales son generalmente mucho más energéticas que las reacciones de fusión individuales , que son a su vez millones de veces más energéticas que las reacciones químicas. Solo la conversión directa de masa en energía , como la causada por la colisión aniquiladora de materia y antimateria , es más energética por unidad de masa que la fusión nuclear. (La conversión completa de un gramo de materia liberaría9 × 10 13 julios de energía.)
En las estrellas
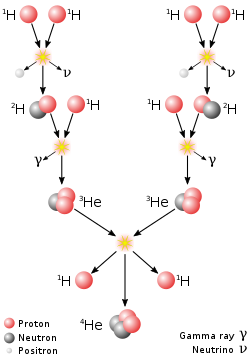
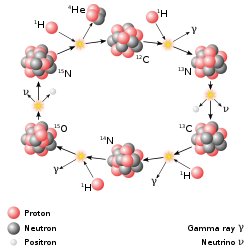
Un importante proceso de fusión es la nucleosíntesis estelar que alimenta a las estrellas , incluido el Sol. En el siglo XX, se reconoció que la energía liberada por las reacciones de fusión nuclear explica la longevidad del calor y la luz estelares. La fusión de núcleos en una estrella, a partir de su abundancia inicial de hidrógeno y helio, proporciona esa energía y sintetiza nuevos núcleos. Intervienen diferentes cadenas de reacciones, dependiendo de la masa de la estrella (y, por tanto, de la presión y la temperatura en su núcleo).
Alrededor de 1920, Arthur Eddington anticipó el descubrimiento y el mecanismo de los procesos de fusión nuclear en las estrellas, en su artículo La constitución interna de las estrellas . [20] [21] En ese momento, la fuente de energía estelar era desconocida; Eddington especuló correctamente que la fuente era la fusión de hidrógeno en helio, liberando una enorme energía de acuerdo con la ecuación de Einstein E = mc 2 . Este fue un desarrollo particularmente notable ya que en ese momento aún no se había descubierto la fusión y la energía termonuclear, ni siquiera que las estrellas están compuestas en gran parte de hidrógeno (ver metalicidad ). El artículo de Eddington razonó que:
- La teoría principal de la energía estelar, la hipótesis de la contracción, debería hacer que la rotación de una estrella se acelere visiblemente debido a la conservación del momento angular . Pero las observaciones de las estrellas variables cefeidas demostraron que esto no estaba sucediendo.
- La única otra fuente plausible de energía conocida era la conversión de materia en energía; Einstein había demostrado algunos años antes que una pequeña cantidad de materia equivalía a una gran cantidad de energía.
- Francis Aston también había demostrado recientemente que la masa de un átomo de helio era aproximadamente un 0,8% menor que la masa de los cuatro átomos de hidrógeno que, combinados, formarían un átomo de helio (según la teoría de la estructura atómica que prevalecía entonces, que sostenía que el peso atómico era la propiedad distintiva entre los elementos; el trabajo de Henry Moseley y Antonius van den Broek demostraría más tarde que la carga nucleica era la propiedad distintiva y que, por lo tanto, un núcleo de helio consistía en dos núcleos de hidrógeno más masa adicional). Esto sugería que si tal combinación pudiera ocurrir, liberaría una energía considerable como subproducto.
- Si una estrella contuviera sólo un 5% de hidrógeno fundible, sería suficiente para explicar cómo las estrellas obtienen su energía. (Hoy en día se sabe que la mayoría de las estrellas "ordinarias" suelen estar compuestas por entre un 70% y un 75% de hidrógeno)
- También podrían fusionarse más elementos, y otros científicos habían especulado que las estrellas eran el "crisol" en el que los elementos ligeros se combinaban para crear elementos pesados, pero sin mediciones más precisas de sus masas atómicas no se podía decir nada más en ese momento.
Todas estas especulaciones resultaron ser correctas en las décadas siguientes.
La fuente principal de energía solar, y la de estrellas de tamaño similar, es la fusión de hidrógeno para formar helio ( reacción en cadena protón-protón ), que ocurre a una temperatura del núcleo solar de 14 millones de kelvin. El resultado neto es la fusión de cuatro protones en una partícula alfa , con la liberación de dos positrones y dos neutrinos (que transforman dos de los protones en neutrones), y energía. En las estrellas más pesadas, el ciclo CNO y otros procesos son más importantes. A medida que una estrella utiliza una fracción sustancial de su hidrógeno, comienza a sintetizar elementos más pesados. Los elementos más pesados se sintetizan por fusión que ocurre cuando una estrella más masiva experimenta una violenta supernova al final de su vida, un proceso conocido como nucleosíntesis de supernova .
Requisitos
This article needs additional citations for verification. (October 2024) |
Para que se produzca la fusión es necesario superar una importante barrera energética de fuerzas electrostáticas. A grandes distancias, dos núcleos desnudos se repelen entre sí debido a la fuerza electrostática repulsiva entre sus protones con carga positiva . Sin embargo, si se logra acercar lo suficiente a dos núcleos, la repulsión electrostática se puede superar mediante el efecto cuántico, en el que los núcleos pueden hacer efecto túnel a través de las fuerzas de Coulomb.
Cuando se añade un nucleón, como un protón o un neutrón , a un núcleo, la fuerza nuclear lo atrae hacia todos los demás nucleones del núcleo (si el átomo es lo suficientemente pequeño), pero principalmente hacia sus vecinos inmediatos debido al corto alcance de la fuerza. Los nucleones en el interior de un núcleo tienen más nucleones vecinos que los de la superficie. Dado que los núcleos más pequeños tienen una mayor relación superficie-volumen, la energía de enlace por nucleón debido a la fuerza nuclear generalmente aumenta con el tamaño del núcleo, pero se acerca a un valor límite correspondiente al de un núcleo con un diámetro de aproximadamente cuatro nucleones. Es importante tener en cuenta que los nucleones son objetos cuánticos . Entonces, por ejemplo, dado que dos neutrones en un núcleo son idénticos entre sí, el objetivo de distinguir uno del otro, como cuál está en el interior y cuál está en la superficie, de hecho no tiene sentido, y, por lo tanto, la inclusión de la mecánica cuántica es necesaria para realizar cálculos adecuados.
La fuerza electrostática, por otra parte, es una fuerza inversamente proporcional al cuadrado , por lo que un protón añadido a un núcleo sentirá una repulsión electrostática de todos los demás protones del núcleo. La energía electrostática por nucleón debida a la fuerza electrostática aumenta sin límite a medida que aumenta el número atómico del núcleo.
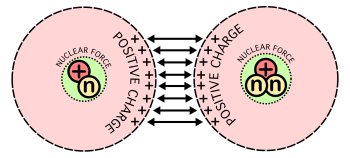
El resultado neto de las fuerzas electrostáticas y nucleares fuertes opuestas es que la energía de enlace por nucleón generalmente aumenta con el aumento del tamaño, hasta los elementos hierro y níquel , y luego disminuye para los núcleos más pesados. Finalmente, la energía de enlace se vuelve negativa y los núcleos muy pesados (todos con más de 208 nucleones, correspondientes a un diámetro de aproximadamente 6 nucleones) no son estables. Los cuatro núcleos más fuertemente unidos, en orden decreciente de energía de enlace por nucleón, son62
Ni
,58
Fé
,56
Fé
, y60
Ni
. [22] Aunque el isótopo de níquel ,62
Ni
, es más estable, el isótopo de hierro 56
Fé
es un orden de magnitud más común. Esto se debe al hecho de que no existe una manera fácil para que las estrellas creen62
Ni
a través del proceso alfa .
Una excepción a esta tendencia general es el núcleo de helio-4 , cuya energía de enlace es mayor que la del litio , el siguiente elemento más pesado. Esto se debe a que los protones y los neutrones son fermiones , que según el principio de exclusión de Pauli no pueden existir en el mismo núcleo en exactamente el mismo estado. El estado de energía de cada protón o neutrón en un núcleo puede acomodar tanto una partícula de espín hacia arriba como una partícula de espín hacia abajo. El helio-4 tiene una energía de enlace anómalamente grande porque su núcleo consta de dos protones y dos neutrones (es un núcleo doblemente mágico ), por lo que sus cuatro nucleones pueden estar en el estado fundamental. Cualquier nucleón adicional tendría que pasar a estados de energía más altos. De hecho, el núcleo de helio-4 está tan fuertemente ligado que comúnmente se lo trata como una sola partícula mecánica cuántica en física nuclear, a saber, la partícula alfa .
La situación es similar si se juntan dos núcleos. A medida que se aproximan, todos los protones de un núcleo repelen a todos los protones del otro. No hasta que los dos núcleos se acercan lo suficiente durante el tiempo suficiente para que la fuerte fuerza de atracción nuclear pueda prevalecer y superar la fuerza electrostática repulsiva. Esto también puede describirse como que los núcleos superan la llamada barrera de Coulomb . La energía cinética para lograr esto puede ser menor que la propia barrera debido al efecto túnel cuántico.
La barrera de Coulomb es la más pequeña para los isótopos del hidrógeno, ya que sus núcleos contienen una sola carga positiva. Un diprotón no es estable, por lo que también deben participar neutrones, idealmente de tal manera que un núcleo de helio, con su enlace extremadamente fuerte, sea uno de los productos.
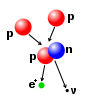
Si se utiliza combustible de deuterio-tritio , la barrera energética resultante es de aproximadamente 0,1 MeV. En comparación, la energía necesaria para extraer un electrón del hidrógeno es de 13,6 eV. El resultado (intermedio) de la fusión es un núcleo inestable de 5 He, que expulsa inmediatamente un neutrón de 14,1 MeV. La energía de retroceso del núcleo de 4 He restante es de 3,5 MeV, por lo que la energía total liberada es de 17,6 MeV. Esto es mucho más de lo que se necesitaba para superar la barrera energética.
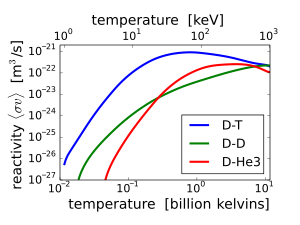
La sección eficaz de reacción (σ) es una medida de la probabilidad de una reacción de fusión en función de la velocidad relativa de los dos núcleos reactivos. Si los reactivos tienen una distribución de velocidades, por ejemplo, una distribución térmica, entonces es útil realizar un promedio sobre las distribuciones del producto de la sección eficaz y la velocidad. Este promedio se denomina "reactividad", denotada ⟨ σv ⟩ . La velocidad de reacción (fusiones por volumen por tiempo) es ⟨ σv ⟩ multiplicada por el producto de las densidades numéricas de los reactivos:
Si una especie de núcleos está reaccionando con un núcleo como él mismo, como en la reacción DD, entonces el producto debe reemplazarse por .
La temperatura ambiente aumenta desde valores prácticamente nulos hasta valores significativos a temperaturas de entre 10 y 100 keV. A estas temperaturas, muy por encima de las energías de ionización típicas (13,6 eV en el caso del hidrógeno), los reactivos de fusión se encuentran en estado de plasma .
La importancia de la función de la temperatura en un dispositivo con un tiempo de confinamiento de energía particular se determina considerando el criterio de Lawson . Esta es una barrera extremadamente difícil de superar en la Tierra, lo que explica por qué la investigación sobre la fusión ha tardado muchos años en alcanzar el estado técnico avanzado actual. [23]
Fusión artificial
Fusión termonuclear
La fusión termonuclear es el proceso de combinación o "fusión" de núcleos atómicos mediante altas temperaturas para acercarlos lo suficiente como para que esto sea posible. Dichas temperaturas hacen que la materia se convierta en un plasma y, si se encuentra confinada, pueden producirse reacciones de fusión debido a colisiones con energías cinéticas térmicas extremas de las partículas. Existen dos formas de fusión termonuclear: la no controlada , en la que la energía resultante se libera de manera descontrolada, como ocurre en las armas termonucleares ("bombas de hidrógeno") y en la mayoría de las estrellas ; y la controlada , en la que las reacciones de fusión tienen lugar en un entorno que permite aprovechar parte o toda la energía liberada con fines constructivos.
La temperatura es una medida de la energía cinética media de las partículas, por lo que al calentar el material ganará energía. Después de alcanzar la temperatura suficiente, dada por el criterio de Lawson , la energía de las colisiones accidentales dentro del plasma es lo suficientemente alta como para superar la barrera de Coulomb y las partículas pueden fusionarse.
En una reacción de fusión de deuterio-tritio , por ejemplo, la energía necesaria para superar la barrera de Coulomb es de 0,1 MeV . Al convertir entre energía y temperatura, se observa que la barrera de 0,1 MeV se superaría a una temperatura superior a 1200 millones de kelvin .
Hay dos efectos que son necesarios para reducir la temperatura real. Uno es el hecho de que la temperatura es la energía cinética promedio , lo que implica que algunos núcleos a esta temperatura en realidad tendrían una energía mucho mayor que 0,1 MeV, mientras que otros serían mucho más bajos. Son los núcleos en la cola de alta energía de la distribución de velocidad los que explican la mayoría de las reacciones de fusión. El otro efecto es el efecto túnel cuántico . Los núcleos en realidad no tienen que tener suficiente energía para superar la barrera de Coulomb por completo. Si tienen energía casi suficiente, pueden atravesar la barrera restante mediante un efecto túnel. Por estas razones, el combustible a temperaturas más bajas seguirá experimentando eventos de fusión, a un ritmo menor.
La fusión termonuclear es uno de los métodos que se están investigando para intentar producir energía de fusión . Si se logra que su uso sea favorable, reduciría significativamente la huella de carbono mundial .
Fusión haz-haz o haz-objetivo
La fusión de iones de luz basada en aceleradores es una técnica que utiliza aceleradores de partículas para lograr energías cinéticas de partículas suficientes para inducir reacciones de fusión de iones de luz. [24]
Acelerar iones ligeros es relativamente fácil y se puede hacer de manera eficiente, requiriendo solo un tubo de vacío, un par de electrodos y un transformador de alto voltaje; la fusión se puede observar con tan solo 10 kV entre los electrodos. [ cita requerida ] El sistema se puede organizar para acelerar iones en un objetivo estático infundido con combustible, conocido como fusión haz-objetivo , o acelerando dos corrientes de iones una hacia la otra, fusión haz-haz . [ cita requerida ] El problema clave con la fusión basada en aceleradores (y con los objetivos fríos en general) es que las secciones transversales de fusión son muchos órdenes de magnitud menores que las secciones transversales de interacción de Coulomb. Por lo tanto, la gran mayoría de iones gastan su energía emitiendo radiación de frenado y la ionización de átomos del objetivo. Los dispositivos conocidos como generadores de neutrones de tubo sellado son particularmente relevantes para esta discusión. Estos pequeños dispositivos son aceleradores de partículas en miniatura llenos de gas deuterio y tritio en una disposición que permite acelerar los iones de esos núcleos contra objetivos de hidruro, que también contienen deuterio y tritio, donde se produce la fusión, lo que libera un flujo de neutrones. Cada año se producen cientos de generadores de neutrones para su uso en la industria petrolera, donde se utilizan en equipos de medición para localizar y cartografiar reservas de petróleo. [ cita requerida ]
A lo largo de los años se han realizado varios intentos de recircular los iones que "no logran" colisionar. Uno de los intentos más conocidos en la década de 1970 fue Migma , que utilizó un anillo de almacenamiento de partículas único para capturar iones en órbitas circulares y devolverlos al área de reacción. Los cálculos teóricos realizados durante las revisiones de financiación señalaron que el sistema tendría dificultades significativas para ampliarse para contener suficiente combustible de fusión para ser relevante como fuente de energía. En la década de 1990, Norman Rostoker propuso una nueva disposición que utiliza una configuración de campo invertido (FRC) como sistema de almacenamiento y TAE Technologies continúa estudiándola en 2021. Un enfoque estrechamente relacionado es fusionar dos FRC que giran en direcciones opuestas, [25] que está siendo estudiado activamente por Helion Energy . Debido a que todos estos enfoques tienen energías de iones mucho más allá de la barrera de Coulomb , a menudo sugieren el uso de ciclos de combustible alternativos como p- 11 B que son demasiado difíciles de intentar utilizando enfoques convencionales. [26][update]
Fusión catalizada por muones
La fusión catalizada por muones es un proceso de fusión que ocurre a temperaturas normales. Fue estudiada en detalle por Steven Jones a principios de los años 1980. La producción de energía neta a partir de esta reacción no ha sido exitosa debido a la alta energía requerida para crear muones , su corta vida media de 2,2 μs y la alta probabilidad de que un muón se una a la nueva partícula alfa y, por lo tanto, deje de catalizar la fusión. [27]
Otros principios

Se han investigado otros principios de confinamiento.
- La fusión con antimateria inicializada utiliza pequeñas cantidades de antimateria para desencadenar una pequeña explosión de fusión. Esto se ha estudiado principalmente en el contexto de hacer viable la propulsión nuclear por pulsos y las bombas de fusión pura . Esto no está ni cerca de convertirse en una fuente de energía práctica, debido al costo de fabricación de antimateria únicamente.
- En abril de 2005, un equipo de la UCLA informó sobre la fusión piroeléctrica . Los científicos utilizaron un cristal piroeléctrico calentado de −34 a 7 °C (−29 a 45 °F), combinado con una aguja de tungsteno para producir un campo eléctrico de unos 25 gigavoltios por metro para ionizar y acelerar los núcleos de deuterio en un objetivo de deuteruro de erbio . En los niveles de energía estimados, [28] puede ocurrir la reacción de fusión D–D, produciendo helio-3 y un neutrón de 2,45 MeV . Aunque es un generador de neutrones útil, el aparato no está destinado a la generación de energía, ya que requiere mucha más energía de la que produce. [29] [30] [31] [32] Se han observado reacciones de fusión D–T con un objetivo de erbio tritiado. [33]
- La fusión nuclear híbrida con fisión (energía nuclear híbrida) es un método propuesto para generar energía mediante el uso de una combinación de procesos de fusión y fisión nuclear . El concepto data de la década de 1950 y fue defendido brevemente por Hans Bethe durante la década de 1970, pero permaneció en gran parte sin explorar hasta que resurgió el interés en 2009, debido a las demoras en la realización de la fusión pura. [34]
- El proyecto PACER , llevado a cabo en el Laboratorio Nacional de Los Álamos (LANL) a mediados de los años 70, exploró la posibilidad de un sistema de energía de fusión que implicaría la explosión de pequeñas bombas de hidrógeno (bombas de fusión) dentro de una cavidad subterránea. Como fuente de energía, el sistema es el único sistema de energía de fusión cuyo funcionamiento podría demostrarse utilizando la tecnología existente. Sin embargo, también requeriría un suministro continuo y de gran tamaño de bombas nucleares, lo que hace que la economía de un sistema de este tipo sea bastante cuestionable.
- La fusión de burbujas, también llamada sonofusión , fue un mecanismo propuesto para lograr la fusión a través de cavitación sónica que ganó prominencia a principios de la década de 2000. Los intentos posteriores de replicación fracasaron y el investigador principal, Rusi Taleyarkhan , fue declarado culpable de mala conducta en la investigación en 2008. [35]
Confinamiento en la fusión termonuclear
El problema clave para lograr la fusión termonuclear es cómo confinar el plasma caliente. Debido a la alta temperatura, el plasma no puede estar en contacto directo con ningún material sólido, por lo que tiene que estar ubicado en el vacío . Además, las altas temperaturas implican altas presiones. El plasma tiende a expandirse inmediatamente y es necesaria cierta fuerza para actuar contra él. Esta fuerza puede tomar una de tres formas: gravitación en las estrellas, fuerzas magnéticas en los reactores de fusión por confinamiento magnético o inercial , ya que la reacción de fusión puede ocurrir antes de que el plasma comience a expandirse, por lo que la inercia del plasma mantiene unido el material.
Confinamiento gravitacional
Una fuerza capaz de confinar el combustible lo suficientemente bien como para satisfacer el criterio de Lawson es la gravedad . Sin embargo, la masa necesaria es tan grande que el confinamiento gravitacional solo se encuentra en las estrellas : las estrellas menos masivas capaces de una fusión sostenida son las enanas rojas , mientras que las enanas marrones pueden fusionar deuterio y litio si tienen suficiente masa. En las estrellas lo suficientemente pesadas , después de que se agote el suministro de hidrógeno en sus núcleos, sus núcleos (o una capa alrededor del núcleo) comienzan a fusionar helio en carbono . En las estrellas más masivas (al menos 8-11 masas solares ), el proceso continúa hasta que parte de su energía se produce fusionando elementos más ligeros con hierro . Como el hierro tiene una de las energías de enlace más altas , las reacciones que producen elementos más pesados son generalmente endotérmicas . Por lo tanto, cantidades significativas de elementos más pesados no se forman durante los períodos estables de evolución de estrellas masivas, sino que se forman en explosiones de supernovas . Algunas estrellas más ligeras también forman estos elementos en las partes externas de las estrellas durante largos períodos de tiempo, absorbiendo energía de la fusión en el interior de la estrella, al absorber los neutrones que se emiten durante el proceso de fusión.
En teoría, todos los elementos más pesados que el hierro tienen algún potencial de liberación de energía. En el extremo extremadamente pesado de la producción de elementos, estos elementos más pesados pueden producir energía en el proceso de división nuevamente hasta alcanzar el tamaño del hierro, en el proceso de fisión nuclear . La fisión nuclear libera así energía que ha estado almacenada, a veces miles de millones de años antes, durante la nucleosíntesis estelar .
Confinamiento magnético
Las partículas cargadas eléctricamente (como los iones de combustible) seguirán las líneas del campo magnético (véase Centro guía ). Por lo tanto, el combustible de fusión puede quedar atrapado utilizando un campo magnético fuerte. Existe una variedad de configuraciones magnéticas, incluidas las geometrías toroidales de los tokamaks y los stellarators y los sistemas de confinamiento de espejos de extremos abiertos.
Confinamiento inercial
Un tercer principio de confinamiento es aplicar un pulso rápido de energía a una gran parte de la superficie de una pastilla de combustible de fusión, haciendo que simultáneamente "implosione" y se caliente a una presión y temperatura muy altas. Si el combustible es lo suficientemente denso y lo suficientemente caliente, la velocidad de reacción de fusión será lo suficientemente alta como para quemar una fracción significativa del combustible antes de que se haya disipado. Para lograr estas condiciones extremas, el combustible inicialmente frío debe comprimirse explosivamente. El confinamiento inercial se utiliza en la bomba de hidrógeno , donde el impulsor son los rayos X creados por una bomba de fisión. El confinamiento inercial también se intenta en la fusión nuclear "controlada", donde el impulsor es un láser , un haz de iones o de electrones , o un Z-pinch . Otro método es utilizar material altamente explosivo convencional para comprimir un combustible a condiciones de fusión. [36] [37] La instalación de implosión impulsada por explosivos UTIAS se utilizó para producir implosiones hemisféricas estables, centradas y enfocadas [38] para generar neutrones a partir de reacciones DD. El método más simple y directo resultó ser el de una mezcla estequiométrica predetonada de deuterio y oxígeno . El otro método exitoso fue el que utilizó un compresor Voitenko en miniatura , [39] donde un diafragma plano era impulsado por la onda de implosión hacia una pequeña cavidad esférica secundaria que contenía gas deuterio puro a una atmósfera. [40]
Confinamiento electrostático
También existen dispositivos de fusión por confinamiento electrostático . Estos dispositivos confinan los iones mediante campos electrostáticos. El más conocido es el fusor . Este dispositivo tiene un cátodo dentro de una jaula de alambre de ánodo. Los iones positivos vuelan hacia la jaula interior negativa y se calientan por el campo eléctrico en el proceso. Si no alcanzan la jaula interior, pueden colisionar y fusionarse. Sin embargo, los iones normalmente golpean el cátodo, lo que crea pérdidas de conducción prohibitivas . Además, las tasas de fusión en los fusores son muy bajas debido a los efectos físicos competitivos, como la pérdida de energía en forma de radiación luminosa. [41] Se han propuesto diseños para evitar los problemas asociados con la jaula, generando el campo utilizando una nube no neutra. Estos incluyen un dispositivo oscilante de plasma, [42] una trampa de Penning y el polywell . [43] Sin embargo, la tecnología es relativamente inmadura y quedan muchas preguntas científicas y de ingeniería.
El método de confinamiento electrostático inercial más conocido es el fusor . A partir de 1999, varios aficionados han podido realizar fusiones amateurs utilizando estos dispositivos caseros. [44] [45] [46] [47] Otros dispositivos IEC incluyen: Polywell , MIX POPS [48] y Marble. [49]
Reacciones importantes
Cadenas de reacción estelares
A las temperaturas y densidades de los núcleos estelares, las tasas de reacciones de fusión son notoriamente lentas. Por ejemplo, a la temperatura del núcleo solar ( T ≈ 15 MK) y densidad (160 g/cm 3 ), la tasa de liberación de energía es de solo 276 μW/cm 3 —aproximadamente una cuarta parte de la tasa volumétrica a la que un cuerpo humano en reposo genera calor. [50] Por lo tanto, la reproducción de las condiciones del núcleo estelar en un laboratorio para la producción de energía de fusión nuclear es completamente impráctica. Debido a que las tasas de reacción nuclear dependen de la densidad así como de la temperatura y la mayoría de los esquemas de fusión operan a densidades relativamente bajas, esos métodos dependen fuertemente de temperaturas más altas. La tasa de fusión en función de la temperatura (exp(− E / kT )), conduce a la necesidad de alcanzar temperaturas en reactores terrestres 10-100 veces más altas que en el interior estelar: T ≈(0,1–1,0) × 10 9 K .
Criterios y candidatos para reacciones terrestres
En la fusión artificial, el combustible primario no está limitado a protones y se pueden utilizar temperaturas más altas, por lo que se eligen reacciones con secciones transversales más grandes. Otra preocupación es la producción de neutrones, que activan radiológicamente la estructura del reactor, pero también tienen la ventaja de permitir la extracción volumétrica de la energía de fusión y la reproducción de tritio . Las reacciones que no liberan neutrones se denominan aneutrónicas .
Para que una reacción de fusión sea una fuente de energía útil, debe cumplir varios criterios. Debe:
- Ser exotérmico
- Esto limita los reactivos al lado Z bajo (número de protones) de la curva de energía de enlace . También hace que el helio4
Él
El producto más común debido a su unión extraordinariamente fuerte, aunque3
Él
y3
yo
También aparecen. - Involucra núcleos de bajo número atómico ( Z )
- Esto se debe a que la repulsión electrostática que debe superarse antes de que los núcleos estén lo suficientemente cerca para fusionarse ( barrera de Coulomb ) está directamente relacionada con el número de protones que contiene: su número atómico.
- Tiene dos reactivos
- En condiciones de densidades inferiores a las estelares, las colisiones entre tres cuerpos son demasiado improbables. En el confinamiento inercial, se superan tanto las densidades estelares como las temperaturas para compensar las deficiencias del tercer parámetro del criterio de Lawson, el brevísimo tiempo de confinamiento del ICF.
- Tener dos o más productos
- Esto permite la conservación simultánea de energía y momento sin depender de la fuerza electromagnética.
- Conservar tanto protones como neutrones
- Las secciones transversales para la interacción débil son demasiado pequeñas.
Pocas reacciones cumplen estos criterios. Las siguientes son las que tienen las secciones transversales más grandes: [51] [52]
(1) 2
1D
+ 3
1yo
→ 4
2Él
( 3,52 MeV ) + número 0 ( 14,06 MeV ) (2i) 2
1D
+ 2
1D
→ 3
1yo
( 1,01 MeV ) + pág + ( 3,02 MeV ) 50% (2ii) → 3
2Él
( 0,82 MeV ) + número 0 ( 2,45 MeV ) 50% (3) 2
1D
+ 3
2Él
→ 4
2Él
( 3,6 MeV ) + pág + ( 14,7 MeV ) (4) 3
1yo
+ 3
1yo
→ 4
2Él
+ 2 en 0 + 11,3 MeV (5) 3
2Él
+ 3
2Él
→ 4
2Él
+ 2 p + + 12,9 MeV (6i) 3
2Él
+ 3
1yo
→ 4
2Él
+ pág + + número 0 + 12,1 MeV 57% (6ii) → 4
2Él
( 4,8 MeV ) + 2
1D
( 9,5 MeV ) 43% (7i) 2
1D
+ 6
3Li
→ 2 4
2Él
+ 22,4 MeV (7ii) → 3
2Él
+ 4
2Él
+ número 0 + 2,56 MeV (7iii) → 7
3Li
+ pág + + 5,0 MeV (7iv) → 7
4Ser
+ número 0 + 3,4 MeV (8) pág + + 6
3Li
→ 4
2Él
( 1,7 MeV ) + 3
2Él
( 2,3 MeV ) (9) 3
2Él
+ 6
3Li
→ 2 4
2Él
+ pág + + 16,9 MeV (10) pág + + 11
5B
→ 3 4
2Él
+ 8,7 MeV
| Nucleosynthesis |
|---|
 |
| Related topics |
|
En las reacciones con dos productos, la energía se divide entre ellos en proporción inversa a sus masas, como se muestra. En la mayoría de las reacciones con tres productos, la distribución de la energía varía. En el caso de las reacciones que pueden dar lugar a más de un conjunto de productos, se indican las proporciones de ramificación.
Algunos candidatos a la reacción pueden eliminarse de inmediato. La reacción D– 6 Li no tiene ninguna ventaja en comparación con p + –11
5B
porque es aproximadamente igual de difícil de quemar pero produce sustancialmente más neutrones a través de2
1D
–2
1D
reacciones secundarias. También hay una p + –7
3Li
reacción, pero la sección eficaz es demasiado baja, excepto posiblemente cuando T i > 1 MeV, pero a temperaturas tan altas una reacción endotérmica, productora directa de neutrones, también se vuelve muy significativa. Finalmente, también hay un p + –9
4Ser
reacción, que no sólo es difícil de quemar, sino9
4Ser
Puede inducirse fácilmente a dividirse en dos partículas alfa y un neutrón.
Además de las reacciones de fusión, las siguientes reacciones con neutrones son importantes para "reproducir" tritio en bombas de fusión "secas" y algunos reactores de fusión propuestos:
La última de las dos ecuaciones era desconocida cuando Estados Unidos realizó la prueba de la bomba de fusión Castle Bravo en 1954. Al ser la segunda bomba de fusión jamás probada (y la primera en utilizar litio), los diseñadores del Castle Bravo "Shrimp" habían comprendido la utilidad del 6 Li en la producción de tritio, pero no se habían dado cuenta de que la fisión del 7 Li aumentaría enormemente el rendimiento de la bomba. Si bien el 7 Li tiene una sección transversal de neutrones pequeña para energías de neutrones bajas, tiene una sección transversal más alta por encima de los 5 MeV. [53] El rendimiento de 15 Mt fue un 150% mayor que el 6 Mt previsto y causó una exposición inesperada a la lluvia radiactiva.
Para evaluar la utilidad de estas reacciones, además de los reactivos, los productos y la energía liberada, es necesario saber algo sobre la sección eficaz nuclear . Cualquier dispositivo de fusión dado tiene una presión de plasma máxima que puede soportar, y un dispositivo económico siempre operaría cerca de este máximo. Dada esta presión, la mayor salida de fusión se obtiene cuando la temperatura se elige de modo que ⟨ σv ⟩ / T 2 sea un máximo. Esta es también la temperatura a la que el valor del producto triple nTτ requerido para la ignición es un mínimo, ya que ese valor requerido es inversamente proporcional a ⟨ σv ⟩ / T 2 (ver criterio de Lawson ). (Un plasma se "enciende" si las reacciones de fusión producen suficiente energía para mantener la temperatura sin calentamiento externo). Esta temperatura óptima y el valor de ⟨ σv ⟩ / T 2 a esa temperatura se dan para algunas de estas reacciones en la siguiente tabla.
| combustible | T [keV] | ⟨σv ⟩ / T 2 [m 3 /s/ keV 2 ] |
|---|---|---|
| 2 1D –3 1yo | 13.6 | 1,24 × 10 −24 |
| 2 1D –2 1D | 15 | 1,28 × 10 −26 |
| 2 1D –3 2Él | 58 | 2,24 × 10 −26 |
| pág + –6 3Li | 66 | 1,46 × 10 −27 |
| pág + –11 5B | 123 | 3,01 × 10 −27 |
Tenga en cuenta que muchas de las reacciones forman cadenas. Por ejemplo, un reactor alimentado con3
1yo
y3
2Él
crea algunos2
1D
, que luego se puede utilizar en el2
1D
–3
2Él
reacción si las energías son "correctas". Una idea elegante es combinar las reacciones (8) y (9).3
2Él
de la reacción (8) puede reaccionar con6
3Li
en la reacción (9) antes de termalizarse completamente. Esto produce un protón energético, que a su vez experimenta la reacción (8) antes de termalizarse. Un análisis detallado muestra que esta idea no funcionaría bien, [ cita requerida ] pero es un buen ejemplo de un caso en el que la suposición habitual de un plasma maxwelliano no es apropiada.
Abundancia de combustibles de fusión nuclear
| Isótopo del combustible de fusión nuclear | Vida media | Abundancia |
|---|---|---|
| 1 1yo [54] [55] [56] [57] [58] [59] [60] [61] | Estable | 99,98% |
| 2 1D [62] [63] [64] [65] | Estable | 0,02% |
| 3 1yo [62] [63] | 12.32(2) años | rastro |
| 3 2Él [62] [63] [64] | estable | 0,0002% |
| 4 2Él [65] | estable | 99,9998% |
| 6 3Li [62] [63] [64] | estable | 7,59% |
| 7 3Li [62] [64] | estable | 92,41% |
| 11 5B [62] [63] [64] [66] | estable | 80% |
| 12 6do [55] [59] | estable | 98,9% |
| 13 6do [55] | estable | 1,1% |
| 13 7norte [55] [59] | 9.965(4) minutos | Sin |
| 14 7norte [55] [56] [59] | estable | 99,6% |
| 15 7norte [55] [56] [57] [59] [60] [64] | estable | 0,4% |
| 14 8Oh [59] | 70.621(11) s | Sin |
| 15 8Oh [55] [56] [59] [60] | 122.266(43) s | Sin |
| 16 8Oh [56] [57] [58] [60] [61] | estable | 99,76% |
| 17 8Oh [56] [57] [58] | estable | 0,04% |
| 18 8Oh [57] [58] | estable | 0,20% |
| 17 9F [56] [57] [58] [60] [61] | 64.370(27) s | Sin |
| 18 9F [57] [58] [60] [61] | 109.734(8) minutos | rastro |
| 19 9F [58] [61] | estable | 100% |
| 18 10Nordeste [60] [61] | 1664,20(47)ms | rastro |
| 19 10Nordeste [61] | 17.2569(19) s | rastro |
Neutronicidad, requisito de confinamiento y densidad de potencia
En principio, cualquiera de las reacciones anteriores puede ser la base de la producción de energía de fusión . Además de la temperatura y la sección eficaz analizadas anteriormente, debemos considerar la energía total de los productos de fusión E fus , la energía de los productos de fusión cargados E ch y el número atómico Z del reactivo no hidrogénico.
Especificación de la2
1D
–2
1D
Sin embargo, la reacción entraña algunas dificultades. Para empezar, hay que hacer un promedio de las dos ramas (2i) y (2ii). Más difícil es decidir cómo tratar la reacción.3
1yo
y3
2Él
productos.3
1yo
arde tan bien en un plasma de deuterio que es casi imposible extraerlo del plasma.2
1D
–3
2Él
La reacción se optimiza a una temperatura mucho más alta, por lo que la combustión en el punto óptimo2
1D
–2
1D
La temperatura puede ser baja, por lo que parece razonable suponer que3
1yo
pero no el3
2Él
se quema y agrega su energía a la reacción neta, lo que significa que la reacción total sería la suma de (2i), (2ii) y (1):
- 52
1D
→4
2Él
+ 2 y 0 +3
2Él
+ p + , E fus = 4,03 + 17,6 + 3,27 = 24,9 MeV, E ch = 4,03 + 3,5 + 0,82 = 8,35 MeV.
Para calcular la potencia de un reactor (en el que la velocidad de reacción está determinada por el paso D–D), contamos2
1D
–2
1D
energía de fusión por reacción D–D como E fus = (4,03 MeV + 17,6 MeV) × 50% + (3,27 MeV) × 50% = 12,5 MeV y la energía en partículas cargadas como E ch = (4,03 MeV + 3,5 MeV) × 50% + (0,82 MeV) × 50% = 4,2 MeV. (Nota: si el ion tritio reacciona con un deuterón mientras todavía tiene una gran energía cinética, entonces la energía cinética del helio-4 producido puede ser bastante diferente de 3,5 MeV, [67] por lo que este cálculo de energía en partículas cargadas es solo una aproximación del promedio.) La cantidad de energía por deuterón consumido es 2/5 de esto, o 5,0 MeV (una energía específica de aproximadamente 225 millones de MJ por kilogramo de deuterio).
Otro aspecto único de la2
1D
–2
1D
La reacción es que solo hay un reactivo, lo cual debe tenerse en cuenta al calcular la velocidad de reacción.
Con esta elección, tabulamos los parámetros para cuatro de las reacciones más importantes.
| combustible | O | Fusible E [MeV] | E- ch [MeV] | neutronicidad |
|---|---|---|---|---|
| 2 1D –3 1yo | 1 | 17.6 | 3.5 | 0,80 |
| 2 1D –2 1D | 1 | 12.5 | 4.2 | 0,66 |
| 2 1D –3 2Él | 2 | 18.3 | 18.3 | ≈0,05 |
| pág + –11 5B | 5 | 8.7 | 8.7 | ≈0,001 |
La última columna es la neutronicidad de la reacción, la fracción de la energía de fusión liberada en forma de neutrones. Este es un indicador importante de la magnitud de los problemas asociados con los neutrones, como el daño por radiación, el blindaje biológico, la manipulación remota y la seguridad. Para las dos primeras reacciones se calcula como ( E fus − E ch )/ E fus . Para las dos últimas reacciones, donde este cálculo daría cero, los valores citados son estimaciones aproximadas basadas en reacciones secundarias que producen neutrones en un plasma en equilibrio térmico.
Por supuesto, los reactivos también deben mezclarse en las proporciones óptimas. Este es el caso cuando cada ion reactivo más sus electrones asociados representan la mitad de la presión. Suponiendo que la presión total es fija, esto significa que la densidad de partículas del ion no hidrogénico es menor que la del ion hidrogénico por un factor de 2/( Z + 1) . Por lo tanto, la velocidad de estas reacciones se reduce por el mismo factor, además de cualquier diferencia en los valores de ⟨ σv ⟩ / T 2 . Por otro lado, debido a que la2
1D
–2
1D
La reacción tiene un solo reactivo y su velocidad es el doble que cuando el combustible se divide entre dos especies hidrogénicas diferentes, creando así una reacción más eficiente.
Por lo tanto, existe una "penalización" de 2/( Z + 1) para los combustibles no hidrogénicos que surge del hecho de que requieren más electrones, que absorben presión sin participar en la reacción de fusión. (Por lo general, es una buena suposición que la temperatura de los electrones será casi igual a la temperatura de los iones. Sin embargo, algunos autores discuten la posibilidad de que los electrones se puedan mantener sustancialmente más fríos que los iones. En tal caso, conocido como "modo de iones calientes", la "penalización" no se aplicaría). Al mismo tiempo, existe una "bonificación" de un factor 2 para2
1D
–2
1D
porque cada ion puede reaccionar con cualquiera de los otros iones, no sólo con una fracción de ellos.
Ahora podemos comparar estas reacciones en la siguiente tabla.
| combustible | ⟨σv⟩ / T2 | penalización/bonificación | reactividad inversa | Criterio de Lawson | densidad de potencia [W/m 3 /kPa 2 ] | relación inversa de la densidad de potencia |
|---|---|---|---|---|---|---|
| 2 1D –3 1yo | 1,24 × 10 −24 | 1 | 1 | 1 | 34 | 1 |
| 2 1D –2 1D | 1,28 × 10 −26 | 2 | 48 | 30 | 0,5 | 68 |
| 2 1D –3 2Él | 2,24 × 10 −26 | 2/3 | 83 | 16 | 0,43 | 80 |
| pág + –6 3Li | 1,46 × 10 −27 | 1/2 | 1700 | 0,005 | 6800 | |
| pág + –11 5B | 3,01 × 10 −27 | 1/3 | 1240 | 500 | 0,014 | 2500 |
El valor máximo de ⟨ σv ⟩ / T 2 se toma de una tabla anterior. El factor de "penalización/bonificación" es el relacionado con un reactivo no hidrogénico o una reacción de una sola especie. Los valores en la columna "reactividad inversa" se obtienen dividiendo1,24 × 10 −24 por el producto de la segunda y tercera columnas. Indica el factor por el cual las otras reacciones ocurren más lentamente que la2
1D
–3
1yo
reacción en condiciones comparables. La columna " criterio de Lawson " pondera estos resultados con E ch y da una indicación de cuánto más difícil es lograr la ignición con estas reacciones, en relación con la dificultad para la2
1D
–3
1yo
reacción. La penúltima columna se denomina "densidad de potencia" y pondera la reactividad práctica mediante E fus . La última columna indica cuánto menor es la densidad de potencia de fusión de las otras reacciones en comparación con la2
1D
–3
1yo
reacción y puede considerarse una medida del potencial económico.
Pérdidas por Bremsstrahlung en plasmas isotrópicos cuasineutrales
Los iones que se fusionan en muchos sistemas nunca se producen solos, sino que se mezclan con electrones que, en conjunto, neutralizan la carga eléctrica de los iones y forman un plasma . Los electrones generalmente tienen una temperatura comparable o superior a la de los iones, por lo que colisionan con ellos y emiten una radiación de rayos X de entre 10 y 30 keV de energía, un proceso conocido como Bremsstrahlung .
El enorme tamaño del Sol y de las estrellas significa que los rayos X producidos en este proceso no escaparán y depositarán su energía nuevamente en el plasma. Se dice que son opacos a los rayos X. Pero cualquier reactor de fusión terrestre será ópticamente delgado para los rayos X de este rango de energía. Los rayos X son difíciles de reflejar, pero se absorben de manera efectiva (y se convierten en calor) en acero inoxidable de menos de mm de espesor (que forma parte del escudo de un reactor). Esto significa que el proceso de bremsstrahlung está sacando energía del plasma, enfriándolo.
La relación entre la potencia de fusión producida y la radiación de rayos X que se pierde en las paredes es un factor de mérito importante. Esta relación se maximiza generalmente a una temperatura mucho más alta que la que maximiza la densidad de potencia (véase la subsección anterior). La siguiente tabla muestra estimaciones de la temperatura óptima y la relación de potencia a esa temperatura para varias reacciones:
| combustible | Ti [ keV ] | Fusión P / Radiación de frenado P |
|---|---|---|
| 2 1D –3 1yo | 50 | 140 |
| 2 1D –2 1D | 500 | 2.9 |
| 2 1D –3 2Él | 100 | 5.3 |
| 3 2Él –3 2Él | 1000 | 0,72 |
| pág + –6 3Li | 800 | 0,21 |
| pág + –11 5B | 300 | 0,57 |
Las proporciones reales de la energía de fusión a la de radiación de frenado probablemente serán significativamente menores por varias razones. En primer lugar, el cálculo supone que la energía de los productos de fusión se transmite completamente a los iones de combustible, que luego pierden energía a los electrones por colisiones, que a su vez pierden energía por radiación de frenado. Sin embargo, como los productos de fusión se mueven mucho más rápido que los iones de combustible, cederán una fracción significativa de su energía directamente a los electrones. En segundo lugar, se supone que los iones en el plasma son puramente iones de combustible. En la práctica, habrá una proporción significativa de iones de impurezas, lo que reducirá la proporción. En particular, los propios productos de fusión deben permanecer en el plasma hasta que hayan cedido su energía, y permanecerán durante algún tiempo después de eso en cualquier esquema de confinamiento propuesto. Finalmente, se han descuidado todos los canales de pérdida de energía que no sean la radiación de frenado. Los dos últimos factores están relacionados. Desde el punto de vista teórico y experimental, el confinamiento de partículas y de energía parecen estar estrechamente relacionados. En un sistema de confinamiento que retenga bien la energía, los productos de fusión se acumularán. Si los productos de fusión se expulsan de manera eficiente, el confinamiento de la energía también será deficiente.
Las temperaturas que maximizan la potencia de fusión en comparación con la radiación de frenado son en todos los casos más altas que la temperatura que maximiza la densidad de potencia y minimiza el valor requerido del producto triple de fusión . Esto no cambiará el punto de operación óptimo para2
1D
–3
1yo
en gran medida porque la fracción de Bremsstrahlung es baja, pero empujará a los otros combustibles a regímenes donde la densidad de potencia relativa2
1D
–3
1yo
es aún más bajo y el confinamiento requerido aún más difícil de lograr.2
1D
–2
1D
y2
1D
–3
2Él
Las pérdidas por radiación de frenado serán un problema grave, posiblemente prohibitivo.3
2Él
–3
2Él
, p + –6
3Li
y p + –11
5B
Las pérdidas por Bremsstrahlung parecen hacer imposible un reactor de fusión que utilice estos combustibles con un plasma isotrópico casi neutro. Se han considerado algunas salidas a este dilema, pero se han rechazado. [68] [69] Esta limitación no se aplica a los plasmas no neutros y anisotrópicos ; sin embargo, estos tienen sus propios desafíos que afrontar.
Descripción matemática de la sección transversal
La fusión según la física clásica
En una imagen clásica, los núcleos pueden entenderse como esferas duras que se repelen entre sí mediante la fuerza de Coulomb, pero que se fusionan una vez que las dos esferas se acercan lo suficiente para entrar en contacto. Si se estima que el radio de un núcleo atómico es de aproximadamente un femtómetro, la energía necesaria para la fusión de dos hidrógenos es:
Esto implicaría que para el núcleo del Sol, que tiene una distribución de Boltzmann con una temperatura de alrededor de 1,4 keV, la probabilidad de que el hidrógeno alcance el umbral es , es decir, la fusión nunca ocurriría. Sin embargo, la fusión en el Sol sí ocurre debido a la mecánica cuántica.
Parametrización de la sección transversal
La probabilidad de que se produzca la fusión aumenta considerablemente en comparación con la imagen clásica, gracias a la difuminación del radio efectivo como la longitud de onda de De Broglie , así como al efecto túnel cuántico a través de la barrera de potencial. Para determinar la velocidad de las reacciones de fusión, el valor de mayor interés es la sección transversal , que describe la probabilidad de que las partículas se fusionen dando un área característica de interacción. Una estimación del área de la sección transversal de fusión a menudo se divide en tres partes:
donde es la sección transversal geométrica, T es la transparencia de la barrera y R son las características de reacción de la reacción.
es del orden del cuadrado de la longitud de onda de De Broglie, donde es la masa reducida del sistema y es la energía del centro de masa del sistema.
T se puede aproximar mediante la transparencia de Gamow, que tiene la forma: donde es el factor de Gamow y proviene de la estimación de la probabilidad de tunelización cuántica a través de la barrera de potencial.
R contiene toda la física nuclear de la reacción específica y toma valores muy diferentes según la naturaleza de la interacción. Sin embargo, para la mayoría de las reacciones, la variación de es pequeña en comparación con la variación del factor de Gamow y, por lo tanto, se aproxima mediante una función llamada factor S astrofísico , , que varía débilmente en energía. Al unir estas dependencias, una aproximación para la sección eficaz de fusión como función de la energía toma la forma:
Se pueden derivar formas más detalladas de la sección transversal a través de modelos basados en la física nuclear y la teoría de la matriz R.
Fórmulas de secciones transversales de fusión
El formulario de física de plasma del Laboratorio de Investigación Naval [70] proporciona la sección transversal total en barns como función de la energía (en keV) de la partícula incidente hacia un ion objetivo en reposo ajustado por la fórmula:
- con los siguientes valores de coeficiente:
| DT(1) | DD(2i) | DD(2ii) | DHe 3 (3) | TT(4) | Los 3 (6) | |
|---|---|---|---|---|---|---|
| A1 | 45,95 | 46.097 | 47,88 | 89,27 | 38.39 | 123.1 |
| A2 | 50200 | 372 | 482 | 25900 | 448 | 11250 |
| A3 | 1,368 × 10 −2 | 4,36 × 10 −4 | 3,08 × 10 −4 | 3,98 × 10 −3 | 1,02 × 10 −3 | 0 |
| A4 | 1.076 | 1.22 | 1.177 | 1.297 | 2.09 | 0 |
| A5 | 409 | 0 | 0 | 647 | 0 | 0 |
Bosch-Hale [71] también informa sobre secciones transversales calculadas con una matriz R que ajusta los datos de observación con coeficientes de aproximación racionales de Padé . Con la energía en unidades de keV y las secciones transversales en unidades de milibarn, el factor tiene la forma:
- , con los valores de los coeficientes:
| DT(1) | DD(2ii) | DHe 3 (3) | El 4 | |
|---|---|---|---|---|
| 31.3970 | 68.7508 | 31.3970 | 34.3827 | |
| A1 | 5,5576 × 10 4 | 5,7501 × 10 6 | 5.3701 × 10 4 | 6,927 × 10 4 |
| A2 | 2.1054 × 10 2 | 2,5226 × 10 3 | 3.3027 × 10 2 | 7,454 × 10 8 |
| A3 | −3,2638 × 10 −2 | 4.5566 × 10 1 | −1,2706 × 10 −1 | 2.050 × 10 6 |
| A4 | 1,4987 × 10 −6 | 0 | 2,9327 × 10 −5 | 5.2002 × 10 4 |
| A5 | 1,8181 × 10 −10 | 0 | −2,5151 × 10 −9 | 0 |
| B1 | 0 | −3,1995 × 10 −3 | 0 | 6,38 × 10 1 |
| B2 | 0 | −8,5530 × 10 −6 | 0 | −9,95 × 10 −1 |
| B3 | 0 | 5,9014 × 10 −8 | 0 | 6,981 × 10 −5 |
| B4 | 0 | 0 | 0 | 1,728 × 10 −4 |
| Rango de energía aplicable [keV] | 0,5–5000 | 0,3–900 | 0,5–4900 | 0,5–550 |
| 2.0 | 2.2 | 2.5 | 1.9 |
dónde
Secciones eficaces nucleares promediadas por Maxwell
En los sistemas de fusión que están en equilibrio térmico, las partículas se encuentran en una distribución de Maxwell-Boltzmann , lo que significa que las partículas tienen un rango de energías centrado alrededor de la temperatura del plasma. El sol, los plasmas confinados magnéticamente y los sistemas de fusión por confinamiento inercial están bien modelados para estar en equilibrio térmico. En estos casos, el valor de interés es la sección transversal de fusión promediada a lo largo de la distribución de Maxwell-Boltzmann. El formulario de física del plasma del Laboratorio de Investigación Naval tabula las reactividades de las secciones transversales de fusión promediadas por Maxwell en .
| Temperatura [keV] | DT(1) | DD(2ii) | DHe 3 (3) | TT(4) | Los 3 (6) |
|---|---|---|---|---|---|
| 1 | 5,5 × 10 −21 | 1,5 × 10 −22 | 1,0 × 10 −26 | 3,3 × 10 −22 | 1,0 × 10 −28 |
| 2 | 2,6 × 10 −19 | 5,4 × 10 −21 | 1,4 × 10 −23 | 7,1 × 10 −21 | 1,0 × 10 −25 |
| 5 | 1,3 × 10 −17 | 1,8 × 10 −19 | 6,7 × 10 −21 | 1,4 × 10 −19 | 2,1 × 10 −22 |
| 10 | 1,1 × 10 −16 | 1,2 × 10 −18 | 2,3 × 10 −19 | 7,2 × 10 −19 | 1,2 × 10 −20 |
| 20 | 4,2 × 10 −16 | 5,2 × 10 −18 | 3,8 × 10 −18 | 2,5 × 10 −18 | 2,6 × 10 −19 |
| 50 | 8,7 × 10 −16 | 2,1 × 10 −17 | 5,4 × 10 −17 | 8,7 × 10 −18 | 5,3 × 10 −18 |
| 100 | 8,5 × 10 −16 | 4,5 × 10 −17 | 1,6 × 10 −16 | 1,9 × 10 −17 | 2,7 × 10 −17 |
| 200 | 6,3 × 10 −16 | 8,8 × 10 −17 | 2,4 × 10 −16 | 4,2 × 10 −17 | 9,2 × 10 −17 |
| 500 | 3,7 × 10 −16 | 1,8 × 10 −16 | 2,3 × 10 −16 | 8,4 × 10 −17 | 2,9 × 10 −16 |
| 1000 | 2,7 × 10 −16 | 2,2 × 10 −16 | 1,8 × 10 −16 | 8,0 × 10 −17 | 5,2 × 10 −16 |
Para las energías los datos se pueden representar mediante:
con T en unidades de keV.
Véase también
- Reactor de prueba de ingeniería de fusión de China
- Fusión fría
- Fusión de enfoque
- Fusenet
- Cohete de fusión
- Generador de impulsos
- Torus europeo conjunto
- Lista de experimentos de fusión
- Lista de ejemplos de Fusor
- Fuente de neutrones
- Energía nuclear
- Física nuclear
- Reactor nuclear
- Tabla periódica
- Potencia pulsada
- Arma de fusión pura
- Diseño de Teller-Ulam
- Cronología de la fusión nuclear
- Proceso triple alfa
Referencias
- ^ "Ask Us: Sun". Cosmicopia . NASA. 2012. Archivado desde el original el 3 de septiembre de 2018 . Consultado el 13 de julio de 2017 .
- ^ Robert S. Mulliken (1975). «William Draper Harkins 1873 - 1951» (PDF) . Memorias biográficas . 46. Academia Nacional de Ciencias: 47–80. Archivado (PDF) desde el original el 10 de mayo de 2017. Consultado el 23 de agosto de 2023 .
- ^ Eddington, AS (2 de septiembre de 1920). «La constitución interna de las estrellas». Nature . 106 (2653): 14–20. Código Bibliográfico :1920Natur.106...14E. doi : 10.1038/106014a0 . S2CID 36422819. Archivado desde el original el 17 de julio de 2022 . Consultado el 25 de marzo de 2020 .
- Reimpreso en: Eddington, AS (octubre de 1920). «La constitución interna de las estrellas». The Scientific Monthly . 11 (4): 297–303. Código Bibliográfico :1920SciMo..11..297E. Archivado desde el original el 17 de agosto de 2022 . Consultado el 17 de agosto de 2022 .
- Reimpreso en: Eddington, AS (octubre de 1920). "La constitución interna de las estrellas". El Observatorio . 43 (557): 341–358. Código Bibliográfico :1920Obs....43..341E. Archivado desde el original el 17 de agosto de 2022 . Consultado el 17 de agosto de 2022 .
- ^ Hund, F. (octubre de 1927). "Zur Deutung der Molekelspektren. I." [Sobre la explicación de los espectros moleculares I.]. Zeitschrift für Physik (en alemán). 40 (10): 742–764. Código bibliográfico : 1927ZPhy...40..742H. doi :10.1007/BF01400234. S2CID 186239503.
- ^ La formación de túneles fue observada independientemente por los científicos soviéticos Grigory Samuilovich Landsberg y Leonid Isaakovich Mandelstam . Véase:
- Landsberg, G.С.; Мандельштам, Л.И. (1928). "Новое явление в рассеянии света (предварительный отчет)" [Un nuevo fenómeno en la dispersión de la luz (informe preliminar)]. Журнал Русского физико-химического общества, Раздел физики [Revista de la Sociedad Rusa Físico-Química, Sección de Física] (en ruso). 60 : 335.
- Landsberg, G.; Mandelstam, L. (1928). "Eine neue Erscheinung bei der Lichtzerstreuung in Krystallen" [Un nuevo fenómeno en el caso de la dispersión de la luz en los cristales]. Die Naturwissenschaften (en alemán). 16 (28): 557–558. Código bibliográfico : 1928NW.....16..557.. doi : 10.1007/BF01506807. S2CID 22492141.
- Landsberg, GS; Mandelstam, LI (1928). "Über die Lichtzerstreuung in Kristallen" [Sobre la dispersión de la luz en los cristales]. Zeitschrift für Physik (en alemán). 50 (11–12): 769–780. Código bibliográfico : 1928ZPhy...50..769L. doi :10.1007/BF01339412. S2CID 119357805.
- ^ Atkinson, R. d'E.; Houtermans, FG (1929). "Zur Frage der Aufbaumöglichkeit der Elemente in Sternen" [Sobre la cuestión de la posibilidad de formar elementos en las estrellas]. Zeitschrift für Physik (en alemán). 54 (9–10): 656–665. Código bibliográfico : 1929ZPhy...54..656A. doi :10.1007/BF01341595. S2CID 123658609.
- ^ Oliphant, MLE; Harteck, P.; Rutherford, E. (1934). "Descargas de 100 kilovoltios en plasmas de deuterio". Actas de la Royal Society A. 144 : 692–714.
- ^ Videmšek, Boštjan (30 de mayo de 2022). «La fusión nuclear podría proporcionar al mundo una fuente ilimitada de energía limpia. Estamos más cerca que nunca de ello». CNN. Archivado desde el original el 13 de diciembre de 2022. Consultado el 13 de diciembre de 2022 .
- ^ Moses, EI (2009). «The National Ignition Facility: Ushering in a new age for high energy dense science» (La instalación nacional de ignición: el inicio de una nueva era para la ciencia de la alta densidad energética). Physics of Plasmas (Physics of Plasmas ). 16 (4): 041006. Bibcode :2009PhPl...16d1006M. doi :10.1063/1.3116505. Archivado desde el original el 12 de agosto de 2020. Consultado el 25 de marzo de 2020 .
- ^ Kramer, David (marzo de 2011). "DOE analiza nuevamente la fusión inercial como fuente potencial de energía limpia". Physics Today . 64 (3): 26–28. Bibcode :2011PhT....64c..26K. doi :10.1063/1.3563814.
- ^ "El Laboratorio Nacional del DOE hace historia al lograr la ignición por fusión". Archivado desde el original el 19 de febrero de 2023. Consultado el 13 de diciembre de 2022 .
- ^ "Progreso en la fusión". ITER . Archivado desde el original el 1 de junio de 2010 . Consultado el 15 de febrero de 2010 .
- ^ "ITER – el camino hacia la nueva energía". ITER . 2014. Archivado desde el original el 22 de septiembre de 2012.
- ^ "El avance de la fusión nuclear hará que miles de millones de dólares fluyan a las nuevas empresas atómicas". Bloomberg.com . 14 de diciembre de 2022. Archivado desde el original el 31 de enero de 2023 . Consultado el 10 de enero de 2023 .
- ^ Insider, Jenny McGrath, Business; Insider, Business (7 de mayo de 2024). "Avance en la fusión: 6 minutos de plasma establecen un nuevo récord en un reactor". ScienceAlert . Consultado el 27 de septiembre de 2024 .
{{cite web}}:|first=tiene nombre genérico ( ayuda )CS1 maint: multiple names: authors list (link) - ^ Shultis, JK y Faw, RE (2002). Fundamentos de la ciencia y la ingeniería nuclear. CRC Press . pág. 151. ISBN 978-0-8247-0834-4.
- ^ Physics Flexbook Archivado el 28 de diciembre de 2011 en Wayback Machine . Ck12.org. Consultado el 19 de diciembre de 2012.
- ^ Bethe, Hans A. (abril de 1950). «La bomba de hidrógeno». Boletín de los científicos atómicos . 6 (4): 99–104, 125–. Código Bibliográfico :1950BuAtS...6d..99B. doi :10.1080/00963402.1950.11461231. Archivado desde el original el 14 de enero de 2023. Consultado el 14 de septiembre de 2018 .
- ^ Smith, Peter F. (2009). Construir para un clima cambiante: el desafío de la construcción, la planificación y la energía. Earthscan. pág. 129. ISBN 978-1-84977-439-0Archivado desde el original el 5 de noviembre de 2023 . Consultado el 20 de junio de 2023 .
- ^ Eddington, AS (octubre de 1920). «La constitución interna de las estrellas». The Scientific Monthly . 11 (4): 297–303. Bibcode :1920Sci....52..233E. doi :10.1126/science.52.1341.233. JSTOR 6491. PMID 17747682. Archivado desde el original el 17 de julio de 2022 . Consultado el 25 de marzo de 2020 .
- ^ Eddington, AS (1916). "Sobre el equilibrio radiativo de las estrellas". Monthly Notices of the Royal Astronomical Society . 77 : 16–35. Bibcode :1916MNRAS..77...16E. doi : 10.1093/mnras/77.1.16 .
- ^ Los núcleos más estrechamente unidos Archivado el 14 de mayo de 2011 en Wayback Machine . Hyperphysics.phy-astr.gsu.edu. Consultado el 17 de agosto de 2011.
- ^ Informe, Science World (23 de marzo de 2013). «¿Qué son los criterios de Lawson o cómo hacer viable la energía de fusión?». Informe de Science World . Archivado desde el original el 3 de agosto de 2021. Consultado el 14 de marzo de 2021 .
- ^ Möller, Sören (2020). Tecnología de aceleradores. Aceleración y detección de partículas. doi :10.1007/978-3-030-62308-1. ISBN 978-3-030-62307-4. S2CID 229610872. Archivado desde el original el 23 de septiembre de 2022 . Consultado el 20 de septiembre de 2022 .
- ^ J. Slough, G. Votroubek y C. Pihl, "Creación de un plasma de alta temperatura mediante la fusión y compresión de plasmoides de configuración invertida de campo supersónico" Nucl. Fusion 51,053008 (2011).
- ^ A. Asle Zaeem et al. "Fusión aneutrónica en colisión de plasmoides dirigidos de manera opuesta" Plasma Physics Reports, vol. 44, n.º 3, págs. 378-386 (2018).
- ^ Jones, SE (1986). "Revisitando la fusión catalizada por muones". Nature . 321 (6066): 127–133. Código Bibliográfico :1986Natur.321..127J. doi :10.1038/321127a0. S2CID 39819102.
- ^ Métodos complementarios para «Observación de la fusión nuclear impulsada por un cristal piroeléctrico» Archivado el 4 de febrero de 2017 en Wayback Machine . Artículo principal Naranjo, B.; Gimzewski, JK; Putterman, S. (2005). «Observación de la fusión nuclear impulsada por un cristal piroeléctrico». Nature . 434 (7037): 1115–1117. Bibcode :2005Natur.434.1115N. doi :10.1038/nature03575. PMID 15858570. S2CID 4407334.
- ^ Fusión de cristales de la UCLA. Rodan.physics.ucla.edu. Consultado el 17 de agosto de 2011. Archivado el 8 de junio de 2015 en Wayback Machine.
- ^ Schewe, Phil y Stein, Ben (2005). "Pirofusión: un dispositivo de fusión nuclear a temperatura ambiente y del tamaño de la palma de la mano". Actualización de noticias de física . 729 (1). Archivado desde el original el 12 de noviembre de 2013 . Consultado el 3 de mayo de 2006 .
- ^ Saliendo del abismo: la fusión nuclear, de verdad Archivado el 22 de enero de 2012 en Wayback Machine . The Christian Science Monitor . (6 de junio de 2005). Consultado el 17 de agosto de 2011.
- ^ Fusión nuclear en el escritorio... ¡de verdad! Archivado el 4 de septiembre de 2016 en Wayback Machine . MSNBC (27 de abril de 2005). Consultado el 17 de agosto de 2011.
- ^ Naranjo, B.; Putterman, S.; Venhaus, T. (2011). "Fusión piroeléctrica utilizando un blanco tritiado". Instrumentos y métodos nucleares en la investigación en física Sección A: Aceleradores, espectrómetros, detectores y equipos asociados . 632 (1): 43–46. Bibcode :2011NIMPA.632...43N. doi :10.1016/j.nima.2010.08.003.
- ^ Gerstner, E. (2009). "Energía nuclear: el regreso de la energía híbrida". Nature . 460 (7251): 25–28. doi : 10.1038/460025a . PMID 19571861.
- ^ Maugh II, Thomas. «Un físico es declarado culpable de mala conducta». Los Angeles Times . Archivado desde el original el 17 de abril de 2019. Consultado el 17 de abril de 2019 .
- ^ F. Winterberg "Superexplosivos metaestables conjeturados formados bajo alta presión para ignición termonuclear Archivado el 3 de marzo de 2023 en Wayback Machine "
- ^ Zhang, Fan; Murray, Stephen Burke; Higgins, Andrew (2005) "Método de detonación súper comprimido y dispositivo para efectuar dicha detonación [ enlace roto ] "
- ^ II Glass y JC Poinssot "TUBO DE CHOQUE IMPULSADO POR IMPLOSIÓN Archivado el 2 de abril de 2023 en Wayback Machine ". NASA
- ^ D. Sagie y II Glass (1982) "Implosiones hemisféricas impulsadas por explosivos para generar plasmas de fusión"
- ^ T. Saito, AK Kudian y II Glass "Medidas de temperatura de un foco de implosión Archivado el 20 de julio de 2012 en Wayback Machine "
- ^ Flujo de iones y reactividad de fusión, caracterización de un foco iónico esféricamente convergente. Tesis doctoral, Dr. Timothy A Thorson, Wisconsin-Madison 1996.
- ^ "Oscilaciones de plasma esféricas, de gran amplitud, estables y de equilibrio térmico en dispositivos de confinamiento electrostático", DC Barnes y Rick Nebel, FÍSICA DE PLASMAS VOLUMEN 5, NÚMERO 7 JULIO DE 1998
- ^ Carr, M.; Khachan, J. (2013). "Un análisis de sonda sesgada de la formación de pozos de potencial en un campo magnético Polywell de beta baja y solo electrones". Physics of Plasmas 20 (5): 052504. Bibcode :2013PhPl...20e2504C. doi :10.1063/1.4804279
- ^ "Foros de Fusor • Página de índice". Fusor.net. Archivado desde el original el 8 de agosto de 2014. Consultado el 24 de agosto de 2014 .
- ^ "¿Construir un reactor de fusión nuclear? No hay problema". Clhsonline.net. 23 de marzo de 2012. Archivado desde el original el 30 de octubre de 2014. Consultado el 24 de agosto de 2014 .
- ^ Danzico, Matthew (23 de junio de 2010). «Bricolaje extremo: construcción de un reactor nuclear casero en Nueva York». Archivado desde el original el 16 de mayo de 2018. Consultado el 30 de octubre de 2014 .
- ^ Schechner, Sam (18 de agosto de 2008). «Ambiciones nucleares: los científicos aficionados obtienen una reacción de la fusión». The Wall Street Journal . Archivado desde el original el 3 de marzo de 2014. Consultado el 24 de agosto de 2014 .
- ^ Park J, Nebel RA, Stange S, Murali SK (2005). "Observación experimental de una esfera de plasma que oscila periódicamente en un dispositivo de confinamiento electrostático inercial enrejado". Phys Rev Lett . 95 (1): 015003. Bibcode :2005PhRvL..95a5003P. doi :10.1103/PhysRevLett.95.015003. PMID 16090625. Archivado desde el original el 23 de octubre de 2020 . Consultado el 25 de agosto de 2020 .
- ^ "Experimento de líneas de haz recirculantes ambipolares múltiples" Presentación del póster, conferencia IEC EE. UU.-Japón 2011, Dr. Alex Klein
- ^ FusEdWeb | Fusion Education. Fusedweb.pppl.gov (9 de noviembre de 1998). Consultado el 17 de agosto de 2011. Archivado el 24 de octubre de 2007 en Wayback Machine.
- ^ M. Kikuchi, K. Lackner y MQ Tran (2012). Física de la fusión. Organismo Internacional de Energía Atómica . p. 22. ISBN 9789201304100Archivado desde el original el 8 de diciembre de 2015 . Consultado el 8 de diciembre de 2015 .
- ^ K. Miyamoto (2005). Física del plasma y fusión nuclear controlada . Springer-Verlag . ISBN. 3-540-24217-1.
- ^ Subsección 4.7.4c Archivado el 16 de agosto de 2018 en Wayback Machine . Kayelaby.npl.co.uk. Consultado el 19 de diciembre de 2012.
- ^ Ciclo CNO#
- ^ abcdefg Ciclo CNO#CNO-I
- ^ abcdefg Ciclo CNO#CNO-II
- ^ abcdefg Ciclo CNO#CNO-III
- ^ abcdefg Ciclo CNO#CNO-IV
- ^ abcdefg Ciclo CNO#HCNO-I
- ^ abcdefg Ciclo CNO#HCNO-II
- ^ abcdefg Ciclo CNO#HCNO-III
- ^ abcdef Fusión nuclear#Criterios y candidatos para reacciones terrestres
- ^ abcde Fusión aneutrónica#Barrera de Coulomb
- ^ abcdef Fusión aneutrónica#Reacciones candidatas
- ^ ab Fusión fría#Falta de productos de reacción esperados
- ^ Fusión aneutrónica#Radiación residual
- ^ Un balance de momento y energía muestra que si el tritio tiene una energía de E T (y usando masas relativas de 1, 3 y 4 para el neutrón, el tritio y el helio), entonces la energía del helio puede ser cualquier cosa desde [(12E T ) 1/2 −(5×17,6MeV+2×E T ) 1/2 ] 2 /25 hasta [(12E T ) 1/2 +(5×17,6MeV+2×E T ) 1/2 ] 2 /25. Para E T = 1,01 MeV, esto da un rango de 1,44 MeV a 6,73 MeV.
- ^ Rider, Todd Harrison (1995). "Limitaciones fundamentales de los sistemas de fusión de plasma que no se encuentran en equilibrio termodinámico". Dissertation Abstracts International . 56–07 (Sección B): 3820. Bibcode :1995PhDT........45R.
- ^ Rostoker, Norman; Binderbauer, Michl y Qerushi, Artan. Limitaciones fundamentales de los sistemas de fusión de plasma que no se encuentran en equilibrio termodinámico. fusion.ps.uci.edu
- ^ Huba, J. (2003). "NRL PLASMA FORMULARY" (PDF) . Catálogo del MIT . Archivado (PDF) del original el 17 de abril de 2018. Consultado el 11 de noviembre de 2018 .
- ^ Bosch, H. S (1993). "Fórmulas mejoradas para secciones transversales de fusión y reactividades térmicas". Fusión nuclear . 32 (4): 611–631. doi :10.1088/0029-5515/32/4/I07. S2CID 55303621.
Lectura adicional
- "¿Qué es la fusión nuclear?". NuclearFiles.org. Archivado desde el original el 28 de septiembre de 2006. Consultado el 12 de enero de 2006 .
- S. Atzeni; J. Meyer-ter-Vehn (2004). "Reacciones de fusión nuclear" (PDF) . La física de la fusión inercial . University of Oxford Press . ISBN 978-0-19-856264-1. Archivado desde el original (PDF) el 24 de enero de 2005.
- G. Brumfiel (22 de mayo de 2006). "El caos podría mantener la fusión bajo control". Nature . doi :10.1038/news060522-2. S2CID 62598131.
- RW Bussard (9 de noviembre de 2006). "¿Debería Google dedicarse a la energía nuclear? Energía nuclear limpia y barata". Google TechTalks . Archivado desde el original el 26 de abril de 2007. Consultado el 18 de abril de 2007 .
- A. Wenisch; R. Kromp; D. Reinberger (noviembre de 2007). "Ciencia o ficción: ¿hay futuro para la energía nuclear?" (PDF) . Instituto Austriaco de Ecología. Archivado (PDF) del original el 26 de enero de 2021. Consultado el 8 de octubre de 2008 .
- M. Kikuchi, K. Lackner y MQ Tran (2012). Física de la fusión. Organismo Internacional de Energía Atómica . p. 22. ISBN 9789201304100Archivado desde el original el 8 de diciembre de 2015 . Consultado el 8 de diciembre de 2015 .
- RK Janev, ed. (1995). Procesos atómicos y moleculares en plasmas de borde de fusión. Springer US . doi :10.1007/978-1-4757-9319-2. ISBN 978-1-4757-9319-2Archivado desde el original el 16 de enero de 2023 . Consultado el 16 de enero de 2023 .
Enlaces externos
- NuclearFiles.org – Un repositorio de documentos relacionados con la energía nuclear.
- Bibliografía comentada sobre fusión nuclear de la Biblioteca Digital Alsos para Asuntos Nucleares
- Formulario de fusión de la NRL Archivado el 26 de octubre de 2020 en Wayback Machine
- "FusiónWiki".







![{\displaystyle E_{\ce {umbral}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {Z_{1}Z_{2}}{r}}{\ce {->[{\text{2 protones}}]}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {e^{2}}{1\ {\ce { fm}}}}\aproximadamente 1,4\ {\ce {MeV}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca1291445cce7787dc6d8b4cdf069e51ab63d0dd)























