Espuma

Forma de la materia
Parte superior de una bebida espumosa
Burbujas de espuma de jabón
Esponja de limpieza

Las espumas son sistemas materiales de dos fases en los que un gas se distribuye en un segundo material no gaseoso, en concreto, en los que las celdas de gas están encerradas por un material líquido o sólido distinto. [1] : 6  [2] : 4  [3] La espuma "puede contener más o menos líquido [o sólido] según las circunstancias", [1] : 6  aunque en el caso de las espumas gas-líquido, el gas ocupa la mayor parte del volumen. [2] : 4  La palabra deriva del alemán medieval y por lo demás obsoleto veim , en referencia a la "espuma que se forma en el vaso una vez que la cerveza ha sido recién servida" (cf. ausgefeimt ). [1] : 1 

Las teorías sobre la formación, estructura y propiedades de la espuma (en física y química física) difieren un poco entre las espumas líquidas y sólidas en que las primeras son dinámicas (por ejemplo, en que se "deforman continuamente"), como resultado de la difusión de gases entre celdas, el drenaje de líquido de la espuma hacia un líquido a granel, etc. [1] : 1–2  Las teorías sobre las espumas líquidas tienen como análogos directos las teorías sobre las emulsiones , [1] : 3  sistemas materiales de dos fases en los que un líquido está encerrado por otro. [4]

En la mayoría de las espumas, el volumen de gas es grande, con finas películas de líquido o sólido que separan las regiones de gas. [ cita requerida ] Una esponja de baño y la cabeza de un vaso de cerveza son ejemplos de espumas; las espumas de jabón también se conocen como jabones . [ no verificado en el cuerpo ]

Las espumas sólidas pueden ser de celdas cerradas o de celdas abiertas . [ cita requerida ] En la espuma de celdas cerradas, el gas forma bolsas discretas, cada una completamente rodeada por el material sólido. En la espuma de celdas abiertas, las bolsas de gas se conectan entre sí. Una esponja de baño es un ejemplo de una espuma de celdas abiertas: [ no verificado en el cuerpo ] el agua fluye fácilmente a través de toda la estructura, desplazando el aire. Una colchoneta para dormir es un ejemplo de un producto compuesto de espuma de celdas cerradas. [ no verificado en el cuerpo ]

Las espumas son ejemplos de medios dispersos . [ no verificado en el cuerpo ] En general, hay gas presente, por lo que se divide en burbujas de gas de diferentes tamaños (es decir, el material es polidisperso [ no verificado en el cuerpo ] ), separadas por regiones líquidas que pueden formar películas, cada vez más delgadas cuando la fase líquida se drena fuera del sistema . [5] [ página necesaria ] Cuando la escala principal es pequeña, es decir, para una espuma muy fina, este medio disperso puede considerarse un tipo de coloide . [ no verificado en el cuerpo ]

La espuma también puede referirse a algo que es análogo a la espuma, como la espuma cuántica . [ no verificado en el cuerpo ]

Estructura

Una espuma es, en muchos casos, un sistema multiescala. [ cita requerida ]

Orden y desorden de las burbujas en una espuma superficial

Una escala es la burbuja: las espumas materiales suelen estar desordenadas y tienen una variedad de tamaños de burbujas. [ cita requerida ] En tamaños mayores, el estudio de espumas idealizadas está estrechamente vinculado a los problemas matemáticos de superficies mínimas y teselaciones tridimensionales , también llamadas panales . [ cita requerida ] La estructura de Weaire-Phelan se informa en una fuente filosófica primaria como la mejor celda unitaria posible (óptima) de una espuma perfectamente ordenada, [6] [ mejor fuente necesaria ] mientras que las leyes de Plateau describen cómo las películas de jabón forman estructuras en espumas. [ cita requerida ]

A una escala menor que la burbuja se encuentra el espesor de la película de espumas metaestables , que puede considerarse una red de películas interconectadas llamadas láminas . [ cita requerida ] Idealmente, las láminas se conectan en tríadas e irradian 120° hacia afuera desde los puntos de conexión, [ según quién? ] conocidos como bordes de meseta . [ cita requerida ]

Una escala aún más baja es la interfaz líquido-aire en la superficie de la película. [ cita requerida ] La mayoría de las veces, esta interfaz está estabilizada por una capa de estructura anfifílica , a menudo hecha de surfactantes , partículas ( emulsión de Pickering ) o asociaciones más complejas. [ cita requerida ]

Formación

Para que se produzca espuma se necesitan varias condiciones: trabajo mecánico, componentes activos superficiales (surfactantes) que reducen la tensión superficial y la formación de espuma es más rápida que su descomposición. Para crear espuma se necesita trabajo (W) para aumentar el área superficial (ΔA):

W = γ Δ A {\displaystyle W=\gamma \Delta A\,\!}

donde γ es la tensión superficial.

Una de las formas de crear espuma es mediante dispersión, donde se mezcla una gran cantidad de gas con un líquido. Un método de dispersión más específico implica inyectar un gas a través de un orificio en un sólido dentro de un líquido. Si este proceso se completa muy lentamente, se puede emitir una burbuja a la vez desde el orificio, como se muestra en la siguiente imagen.

A continuación se muestra una de las teorías para determinar el tiempo de separación; sin embargo, si bien esta teoría produce datos teóricos que coinciden con los datos experimentales, el desprendimiento debido a la capilaridad se acepta como una mejor explicación.

Burbuja ascendente desde el orificio

La fuerza de flotabilidad actúa para elevar la burbuja, que es

F b = V g ( ρ 2 − ρ 1 ) {\displaystyle F_{b}=Vg(\rho _{2}-\rho _{1})\!}

donde es el volumen de la burbuja, es la aceleración debida a la gravedad, y ρ 1 es la densidad del gas ρ 2 es la densidad del líquido. La fuerza que trabaja en contra de la fuerza de flotabilidad es la fuerza de tensión superficial , que es V {\displaystyle V} g {\displaystyle g}

F s = 2 r π γ {\displaystyle F_{s}=2r\pi \gamma \!} ,

donde γ es la tensión superficial y es el radio del orificio. A medida que se introduce más aire en la burbuja, la fuerza de flotabilidad crece más rápido que la fuerza de tensión superficial. Por lo tanto, el desprendimiento se produce cuando la fuerza de flotabilidad es lo suficientemente grande como para superar la fuerza de tensión superficial. r {\displaystyle r}

V g ( ρ 2 − ρ 1 ) > 2 r π γ {\displaystyle Vg(\rho _{2}-\rho _{1})>2r\pi \gamma \!}

Además, si se trata la burbuja como una esfera con un radio de y se sustituye el volumen en la ecuación anterior, la separación se produce en el momento en que R {\displaystyle R} V {\displaystyle V}

R 3 = 3 r γ 2 g ( ρ 2 − ρ 1 ) {\displaystyle R^{3}={\frac {3r\gamma }{2g(\rho _{2}-\rho _{1})}}\!}

Si examinamos este fenómeno desde el punto de vista de la capilaridad en el caso de una burbuja que se forma muy lentamente, podemos suponer que la presión en el interior es constante en todas partes. La presión hidrostática en el líquido se designa mediante . El cambio de presión en la interfaz entre el gas y el líquido es igual a la presión capilar; por lo tanto, p {\displaystyle p} p 0 {\displaystyle p_{0}}

p − p 0 = γ ( 1 R 1 + 1 R 2 ) {\displaystyle p-p_{0}=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)\!}

donde R 1 y R 2 son los radios de curvatura y se establecen como positivos. En el vástago de la burbuja, R 3 y R 4 son los radios de curvatura que también se consideran positivos. Aquí, la presión hidrostática en el líquido debe tener en cuenta z, la distancia desde la parte superior hasta el vástago de la burbuja. La nueva presión hidrostática en el vástago de la burbuja es p 0 ( ρ 1  −  ρ 2 ) z . La presión hidrostática equilibra la presión capilar, que se muestra a continuación:

p − p 0 − ( ρ 2 − ρ 1 ) g z = γ ( 1 R 3 + 1 R 4 ) {\displaystyle p-p_{0}-(\rho _{2}-\rho _{1})gz=\gamma \left({\frac {1}{R_{3}}}+{\frac {1}{R_{4}}}\right)\!}

Finalmente, la diferencia entre la presión superior e inferior es igual al cambio en la presión hidrostática:

( ρ 2 − ρ 1 ) g z = γ ( 1 R 1 + 1 R 2 − 1 R 3 − 1 R 4 ) {\displaystyle (\rho _{2}-\rho _{1})gz=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}-{\frac {1}{R_{3}}}-{\frac {1}{R_{4}}}\right)\!}

En el tallo de la burbuja, la forma de la misma es casi cilíndrica; en consecuencia, R 3 o R 4 es grande mientras que el otro radio de curvatura es pequeño. A medida que el tallo de la burbuja crece en longitud, se vuelve más inestable ya que uno de los radios crece y el otro se encoge. En un punto determinado, la longitud vertical del tallo excede la circunferencia del tallo y debido a las fuerzas de flotabilidad, la burbuja se separa y el proceso se repite. [7]

Estabilidad

Estabilización

La estabilización de una espuma es causada por fuerzas de van der Waals entre las moléculas de la espuma, capas dobles eléctricas creadas por surfactantes dipolares y el efecto Marangoni , que actúa como una fuerza restauradora de las láminas.

El efecto Marangoni depende de que el líquido que forma espuma sea impuro. Generalmente, los surfactantes en la solución disminuyen la tensión superficial. Los surfactantes también se aglutinan en la superficie y forman una capa como se muestra a continuación.

Para que se produzca el efecto Marangoni, la espuma debe quedar hundida como se muestra en la primera imagen. Esta hundimiento aumenta la superficie local. Los surfactantes tienen un tiempo de difusión mayor que la masa de la solución, por lo que están menos concentrados en el hundimiento.

Además, el estiramiento de la superficie hace que la tensión superficial del punto marcado sea mayor que la del área circundante. En consecuencia, dado que el tiempo de difusión de los surfactantes es grande, el efecto Marangoni tiene tiempo para tener lugar. La diferencia en la tensión superficial crea un gradiente, que provoca el flujo de fluido desde áreas de menor tensión superficial a áreas de mayor tensión superficial. La segunda imagen muestra la película en equilibrio después de que se haya producido el efecto Marangoni. [8]

El curado de una espuma la solidifica, volviéndola indefinidamente estable a temperaturas normales. [9]

Desestabilización

Witold Rybczynski y Jacques Hadamard desarrollaron una ecuación para calcular la velocidad de las burbujas que se elevan en la espuma con el supuesto de que las burbujas son esféricas con un radio . r {\displaystyle r}

u = 2 g r 2 9 η 2 ( ρ 2 − ρ 1 ) ( 3 η 1 + 3 η 2 3 η 1 + 2 η 2 ) {\displaystyle u={\frac {2gr^{2}}{9\eta _{2}}}(\rho _{2}-\rho _{1})\left({\frac {3\eta _{1}+3\eta _{2}}{3\eta _{1}+2\eta _{2}}}\right)\!}

con velocidad en unidades de centímetros por segundo. ρ 1 y ρ 2 es la densidad de un gas y un líquido respectivamente en unidades de g/cm 3 y ῃ 1 y ῃ 2 es la viscosidad dinámica del gas y el líquido respectivamente en unidades de g/cm·s y g es la aceleración de la gravedad en unidades de cm/s 2 .

Sin embargo, dado que la densidad y la viscosidad de un líquido son mucho mayores que las del gas, se pueden descuidar la densidad y la viscosidad del gas, lo que produce la nueva ecuación para la velocidad de ascenso de las burbujas como:

u = g r 2 3 η 2 ( ρ 2 ) {\displaystyle u={\frac {gr^{2}}{3\eta _{2}}}(\rho _{2})\!}

Sin embargo, mediante experimentos se ha demostrado que un modelo más preciso para el ascenso de las burbujas es:

u = 2 g r 2 9 η 2 ( ρ 2 − ρ 1 ) {\displaystyle u={\frac {2gr^{2}}{9\eta _{2}}}(\rho _{2}-\rho _{1})\!}

Las desviaciones se deben al efecto Marangoni y a la presión capilar, que afectan la suposición de que las burbujas son esféricas. Para la presión de Laplace de una interfaz curvada entre gas y líquido, los dos radios de curvatura principales en un punto son R 1 y R 2 . [10] Con una interfaz curva, la presión en una fase es mayor que la presión en otra fase. La presión capilar P c se da mediante la ecuación de:

P c = γ ( 1 R 1 + 1 R 2 ) {\displaystyle P_{c}=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)\!} ,

donde es la tensión superficial. La burbuja que se muestra a continuación es un gas (fase 1) en un líquido (fase 2) y el punto A designa la parte superior de la burbuja mientras que el punto B designa la parte inferior de la burbuja. γ {\displaystyle \gamma }

Burbuja para presión hidrostática

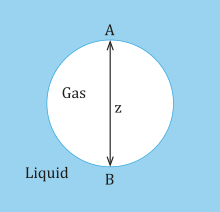
En la parte superior de la burbuja en el punto A, se supone que la presión en el líquido es p 0, al igual que en el gas. En la parte inferior de la burbuja en el punto B, la presión hidrostática es:

P B , 1 = p 0 + g ρ 1 z {\displaystyle P_{B},1=p_{0}+g\rho _{1}z\!}
P B , 2 = p 0 + g ρ 2 z {\displaystyle P_{B},2=p_{0}+g\rho _{2}z\!}

donde ρ 1 y ρ 2 son la densidad de un gas y un líquido respectivamente. La diferencia de presión hidrostática en la parte superior de la burbuja es 0, mientras que la diferencia de presión hidrostática en la parte inferior de la burbuja a través de la interfaz es gz ( ρ 2  −  ρ 1 ). Suponiendo que los radios de curvatura en el punto A son iguales y se denotan por R A y que los radios de curvatura en el punto B son iguales y se denotan por R B , entonces la diferencia de presión capilar entre el punto A y el punto B es:

P c = 2 γ ( 1 R A − 1 R B ) {\displaystyle P_{c}=2\gamma \left({\frac {1}{R_{A}}}-{\frac {1}{R_{B}}}\right)\!}

En el equilibrio, la diferencia de presión capilar debe compensarse con la diferencia de presión hidrostática. Por lo tanto,

g z ( ρ 2 − ρ 1 ) = 2 γ ( 1 R A − 1 R B ) {\displaystyle gz(\rho _{2}-\rho _{1})=2\gamma \left({\frac {1}{R_{A}}}-{\frac {1}{R_{B}}}\right)\!}

Como la densidad del gas es menor que la densidad del líquido, el lado izquierdo de la ecuación siempre es positivo. Por lo tanto, la inversa de R A debe ser mayor que R B. Esto significa que desde la parte superior de la burbuja hasta la parte inferior de la misma el radio de curvatura aumenta. Por lo tanto, sin descuidar la gravedad, las burbujas no pueden ser esféricas. Además, a medida que z aumenta, esto también provoca la diferencia en R A y R B , lo que significa que la burbuja se desvía más de su forma cuanto más grande se hace. [7]

La desestabilización de la espuma se produce por varias razones. En primer lugar, la gravedad provoca el drenaje del líquido hacia la base de la espuma, que Rybczynski y Hadamar incluyen en su teoría; sin embargo, la espuma también se desestabiliza debido a la presión osmótica que provoca el drenaje desde las láminas hasta los bordes de la meseta debido a las diferencias de concentración interna en la espuma, y ​​la presión de Laplace provoca la difusión del gas desde las burbujas pequeñas a las grandes debido a la diferencia de presión. Además, las películas pueden romperse bajo presión de separación . Estos efectos pueden provocar una reorganización de la estructura de la espuma a escalas mayores que las burbujas, que puede ser individual ( proceso T1 ) o colectiva (incluso del tipo "avalancha").

Propiedades mecánicas

Espumas liquidas

Espumas sólidas

Las espumas sólidas, tanto de celdas abiertas como cerradas, se consideran una subclase de estructuras celulares. A menudo tienen una conectividad nodal menor [ jerga ] en comparación con otras estructuras celulares como los panales de abeja y las celosías de celosía y, por lo tanto, su mecanismo de falla está dominado por la flexión de los miembros. La baja conectividad nodal y el mecanismo de falla resultante conducen en última instancia a su menor resistencia mecánica y rigidez en comparación con los panales de abeja y las celosías de celosía. [11] [12]

La resistencia de las espumas puede verse afectada por la densidad, el material utilizado y la disposición de la estructura celular (abierta vs. cerrada e isotropía de poros). [ cita requerida ] Para caracterizar las propiedades mecánicas de las espumas, se utilizan curvas de esfuerzo-deformación de compresión para medir su resistencia y capacidad de absorber energía, ya que este es un factor importante en las tecnologías basadas en espumas. [ cita requerida ]

Espuma elastomérica

En el caso de los sólidos celulares elastoméricos , a medida que la espuma se comprime, primero se comporta elásticamente a medida que las paredes celulares se doblan, luego, a medida que las paredes celulares se pandean, se produce fluencia y ruptura del material hasta que finalmente las paredes celulares se aplastan entre sí y el material se rompe. [13] Esto se ve en una curva de tensión-deformación como un régimen elástico lineal empinado, un régimen lineal con una pendiente suave después de la fluencia (tensión de meseta) y un régimen de aumento exponencial. La rigidez del material se puede calcular a partir del régimen elástico lineal [14] donde el módulo para espumas de celdas abiertas se puede definir mediante la ecuación:

Curva esquemática de tensión-deformación de una espuma elastomérica, que muestra las tres regiones que son elástica lineal, pandeo de la pared celular y fractura de la pared celular, donde el área bajo la curva especificada representa la energía por unidad de volumen que la espuma puede absorber. [ cita requerida ]

( E ∗ E s ) f = C f ( ρ ∗ ρ s ) 2 {\displaystyle \left({\frac {E^{*}}{E_{s}}}\right)_{f}=C_{f}\left({\frac {\rho ^{*}}{\rho _{s}}}\right)^{2}}

donde es el módulo del componente sólido, es el módulo de la estructura de panal, es una constante que tiene un valor cercano a uno, es la densidad de la estructura de panal y es la densidad del sólido. El módulo elástico para espumas de celdas cerradas se puede describir de manera similar mediante: E s {\displaystyle E_{s}} E ∗ {\displaystyle E^{*}} C f {\displaystyle C_{f}} ρ ∗ {\displaystyle \rho ^{*}} ρ s {\displaystyle \rho _{s}}

( E ∗ E s ) f = C f ( ρ ∗ ρ s ) 3 {\displaystyle \left({\frac {E^{*}}{E_{s}}}\right)_{f}=C_{f}\left({\frac {\rho ^{*}}{\rho _{s}}}\right)^{3}}

donde la única diferencia es el exponente en la dependencia de la densidad. Sin embargo, en materiales reales, una espuma de celda cerrada tiene más material en los bordes de la celda, lo que hace que siga más de cerca la ecuación para espumas de celda abierta. [15] La relación de la densidad de la estructura de panal en comparación con la estructura sólida tiene un gran impacto en el módulo del material. En general, la resistencia de la espuma aumenta con la densidad de la celda y la rigidez del material de la matriz.

Energía de deformación

Otra propiedad importante que se puede deducir de la curva de tensión-deformación es la energía que la espuma es capaz de absorber. El área bajo la curva (especificada como antes de la densificación rápida en el pico de tensión) representa la energía en la espuma en unidades de energía por unidad de volumen. La energía máxima almacenada por la espuma antes de la ruptura se describe mediante la ecuación: [13]

W m a x E s = 0.05 ( ρ ∗ ρ s ) 2 [ 0.975 − 1.4 ( ρ ∗ ρ s ) ] {\displaystyle {\frac {W_{max}}{E_{s}}}=0.05\left({\frac {\rho ^{*}}{\rho _{s}}}\right)^{2}\left[0.975-1.4\left({\frac {\rho ^{*}}{\rho _{s}}}\right)\right]}

Esta ecuación se deriva de la hipótesis de una espuma idealizada con aproximaciones de ingeniería a partir de resultados experimentales. La mayor parte de la absorción de energía se produce en la región de tensión de meseta después del régimen elástico lineal pronunciado. [ cita requerida ]

Dependencia direccional

La isotropía de la estructura celular y la absorción de fluidos también pueden tener un impacto en las propiedades mecánicas de una espuma. Si hay anisotropía, la respuesta de los materiales a la tensión dependerá de la dirección y, por lo tanto, la curva de tensión-deformación, el módulo y la absorción de energía variarán según la dirección de la fuerza aplicada. [16] Además, las estructuras de celdas abiertas que tienen poros conectados pueden permitir que el agua u otros líquidos fluyan a través de la estructura, lo que también puede afectar la rigidez y las capacidades de absorción de energía. [17]

Aplicaciones

Espumas liquidas

Las espumas líquidas se pueden utilizar en espumas retardantes de fuego , como las que se utilizan para extinguir incendios, especialmente incendios de petróleo . [ cita requerida ]

La masa del pan leudado se ha entendido tradicionalmente como una espuma de celdas cerradas ( la levadura hace que el pan suba a través de pequeñas burbujas de gas que se convierten en los poros del pan ), donde las celdas no se conectan entre sí. Al cortar la masa se libera el gas de las burbujas que se cortan, pero el gas del resto de la masa no puede escapar. [ cita requerida ] Cuando se permite que la masa suba demasiado, se convierte en una espuma de celdas abiertas, en la que las bolsas de gas están conectadas; cortar la superficie de la masa en ese punto haría que se escape un gran volumen de gas y la masa colapse. [ cita requerida ] [18] Investigaciones recientes han indicado que la estructura de poros del pan está interconectada en un 99% en una gran vacuola, por lo que la espuma de celdas cerradas de la masa húmeda se transforma en una espuma sólida de celdas abiertas en el pan. [ 19 ] [ fuente no primaria necesaria ]

La propiedad única de las espumas gas-líquido de tener una superficie específica muy alta se aprovecha en los procesos químicos de flotación y fraccionamiento de espuma . [ cita requerida ]

Despoblación

La despoblación con espuma o aplicación de espuma es un medio de matar en masa a animales de granja rociando espuma sobre un área extensa para obstruir la respiración y, en última instancia, causar asfixia. [20] [21] Generalmente se utiliza para intentar detener la propagación de enfermedades. [22]

Espumas sólidas

Las espumas sólidas son una clase de materiales de ingeniería celular livianos. Estas espumas se clasifican típicamente en dos tipos según su estructura de poros: espumas con estructura de celdas abiertas (también conocidas como espumas reticuladas ) y espumas de celdas cerradas. Con resoluciones de celdas suficientemente altas, cualquier tipo puede tratarse como material continuo o "continuo" y se denominan sólidos celulares [23] , con propiedades mecánicas predecibles.

Una espuma metálica de celda abierta

Las espumas de celdas abiertas se pueden utilizar para filtrar el aire. Por ejemplo, se ha demostrado que una espuma con catalizador incorporado convierte catalíticamente el formaldehído en sustancias inocuas cuando el aire contaminado con formaldehído pasa a través de la estructura de celdas abiertas. [24]

Las espumas de estructura de celdas abiertas contienen poros que están conectados entre sí y forman una red interconectada que es relativamente blanda. Las espumas de celdas abiertas se llenan con cualquier gas que las rodee. Si se llenan con aire, resultan relativamente buenos aislantes, pero si las celdas abiertas se llenan con agua, las propiedades aislantes se reducirían. Estudios recientes se han centrado en estudiar las propiedades de las espumas de celdas abiertas como material aislante. Se han producido bioespumas de gluten de trigo/TEOS , que muestran propiedades aislantes similares a las de las espumas obtenidas a partir de recursos derivados del petróleo. [25] La gomaespuma es un tipo de espuma de celdas abiertas.

Una espuma metálica de celda cerrada

Las espumas de celdas cerradas no tienen poros interconectados. Las espumas de celdas cerradas normalmente tienen una mayor resistencia a la compresión debido a sus estructuras. Sin embargo, las espumas de celdas cerradas también son, en general, más densas, requieren más material y, como consecuencia, son más caras de producir. Las celdas cerradas se pueden rellenar con un gas especializado para proporcionar un mejor aislamiento. Las espumas de estructura de celdas cerradas tienen una mayor estabilidad dimensional, coeficientes de absorción de humedad bajos y mayor resistencia en comparación con las espumas de estructura de celdas abiertas. Todos los tipos de espuma se utilizan ampliamente como material de núcleo en materiales compuestos con estructura tipo sándwich .

El primer uso conocido de los sólidos celulares en ingeniería es la madera, que en su forma seca es una espuma de celdas cerradas compuesta de lignina, celulosa y aire. A principios del siglo XX, se empezaron a utilizar varios tipos de espumas sólidas fabricadas especialmente. La baja densidad de estas espumas las convierte en excelentes aislantes térmicos y dispositivos de flotación, y su ligereza y compresibilidad las convierten en materiales ideales para embalajes y rellenos.

Un ejemplo del uso de azodicarbonamida [26] como agente de expansión se encuentra en la fabricación de espumas de vinilo (PVC) y EVA-PE , donde desempeña un papel en la formación de burbujas de aire al descomponerse en gas a alta temperatura. [27] [28] [29]

La geometría aleatoria o "estocástica" de estas espumas también las hace buenas para la absorción de energía. A fines del siglo XX y principios del siglo XXI, las nuevas técnicas de fabricación permitieron lograr una geometría que da como resultado una excelente resistencia y rigidez en relación con el peso. Estos nuevos materiales se conocen generalmente como sólidos celulares diseñados. [23]

Espuma sintáctica

Espuma integral para la piel

La espuma de piel integral , también conocida como espuma de piel propia , es un tipo de espuma con una piel de alta densidad y un núcleo de baja densidad. Se puede formar en un proceso de molde abierto o un proceso de molde cerrado . En el proceso de molde abierto, se mezclan dos componentes reactivos y se vierten en un molde abierto. Luego, el molde se cierra y se deja que la mezcla se expanda y se cure. Los ejemplos de artículos producidos utilizando este proceso incluyen reposabrazos , asientos para bebés , suelas de zapatos y colchones . El proceso de molde cerrado, más comúnmente conocido como moldeo por inyección de reacción (RIM), inyecta los componentes mezclados en un molde cerrado a altas presiones. [30]

Escalas y propiedades de la espuma

Véase también

Referencias

  1. ^ abcde Weaire, D y Hutzler, S (1999). La física de las espumas. Oxford, Inglaterra: Oxford University Press. ISBN 0198510977. Consultado el 30 de agosto de 2024 .{{cite book}}: CS1 maint: multiple names: authors list (link) Tenga en cuenta que esta fuente se centra únicamente en espumas líquidas.
  2. ^ ab Cantat, yo ; Cohen-Addad, S; Elías, F; Graner, F; Höhler, R; Pitois, O; Rouyer, F y Saint-Jalmes, A (2013). Espumas: Estructura y Dinámica. Oxford, Inglaterra: Oxford University Press. ISBN 978-0199662890. Consultado el 30 de agosto de 2024 .{{cite book}}: CS1 maint: multiple names: authors list (link) Tenga en cuenta que esta fuente también se centra en las espumas líquidas.
  3. ^ El uso general del término, que incluye tanto formas nominales como verbales, es a la vez más limitado y más amplio que el de la ciencia de los materiales descrito aquí. En el uso general, es más limitado, ya que se refiere con mayor frecuencia a espumas líquidas; es más amplio porque incluye todas las formas de las mismas y las acciones para producirlas, por lo tanto, según Merriam-Webster , el término se refiere a "una masa ligera y espumosa de burbujas finas formadas en o sobre la superficie de un líquido o a partir de un líquido", dando los ejemplos de las producidas por "salivación o sudoración", las producidas de manera estable para combatir incendios, las que son el producto de burbujas de gas introducidas durante la fabricación y luego los ejemplos más amplios de espuma de mar, y luego cualquier cosa que se parezca a lo anterior. Finalmente, la definición general incluye acciones para producir todo lo anterior. Ver "Espuma". Merriam-Webster . Archivado desde el original el 9 de diciembre de 2014.
  4. ^ IUPAC (1997). "Emulsión". Compendio de terminología química (El "Libro de oro") . Oxford: Blackwell Scientific Publications . doi :10.1351/goldbook.E02065. ISBN. 978-0-9678550-9-7. Archivado desde el original el 10 de marzo de 2012.{{cite book}}: CS1 maint: bot: original URL status unknown (link)
  5. ^ Lucassen, J. (1981). Lucassen-Reijnders, EH (ed.). Tensioactivos aniónicos: química física de la acción tensioactiva . Nueva York, Estados Unidos: Marcel Dekker.[ página necesaria ]
  6. ^ Morgan, F. (2008). "Existencia de particiones de perímetro mínimo". Philosophical Magazine Letters . 88 (9–10): 647–650. arXiv : 0711.4228 . Código Bibliográfico :2008PMagL..88..647M. doi :10.1080/09500830801992849.
  7. ^ ab Bikerman, JJ "Formación y estructura" en Foams New York, Springer-Verlag, 1973. cap. 2. sec. 24-25
  8. ^ "La espuma" (PDF) . IHC News . Enero de 2009. Archivado desde el original (PDF) el 12 de diciembre de 2013. Consultado el 9 de diciembre de 2013 .
  9. ^ Stevenson, Paul (3 de enero de 2012). Ingeniería de espuma: fundamentos y aplicaciones. John Wiley & Sons. ISBN 9781119961093.
  10. ^ Wilson, AJ, "Principios de formación y estabilidad de la espuma". Espumas: física, química y estructura . Nueva York, Springer-Verlag, 1989, cap. 1
  11. ^ Queheillalt, Douglas T.; Wadley, Haydn NG (enero de 2005). “Celosías metálicas celulares con cerchas huecas”. Acta Materialia . 53 (2): 303–313. Código Bib : 2005AcMat..53..303Q. doi :10.1016/j.actamat.2004.09.024.
  12. ^ Kooistra, Gregory W.; Deshpande, Vikram S.; Wadley, Haydn NG (agosto de 2004). "Comportamiento a la compresión de estructuras de celosía tetraédrica endurecibles por envejecimiento fabricadas en aluminio". Acta Materialia . 52 (14): 4229–4237. Código Bib : 2004AcMat..52.4229K. doi :10.1016/j.actamat.2004.05.039. S2CID  13958881.
  13. ^ ab Courtney, Thomas H. (2005). Comportamiento mecánico de los materiales . Waveland Press, Inc., págs. 686-713. ISBN 1-57766-425-6.
  14. ^ M. Liu et al. Modelado multiescala de propiedades elásticas efectivas de materiales porosos llenos de fluidos International Journal of Solids and Structures (2019) 162, 36-44
  15. ^ Ashby, MF (1983). "Las propiedades mecánicas de los sólidos celulares". Metallurgical Transactions . 14A (9): 1755–1769. Bibcode :1983MTA....14.1755A. doi :10.1007/bf02645546. S2CID  135765088.
  16. ^ Li, Pei; Guo, YB; Shim, VPW (2020). "Un modelo constitutivo sensible a la velocidad para materiales celulares anisotrópicos: aplicación a una espuma de poliuretano transversalmente isotrópica". Revista internacional de sólidos y estructuras . 206 : 43–58. doi :10.1016/j.ijsolstr.2020.08.007. S2CID  225310568 – vía Elsevier.
  17. ^ Yu, YJ; Hearon, K.; Wilson, TS; Maitland, DJ (2011). "El efecto de la absorción de humedad en las propiedades físicas de las espumas de polímeros de poliuretano con memoria de forma". Materiales y estructuras inteligentes . 20 (8). Código Bibliográfico :2011SMaS...20h5010Y. doi :10.1088/0964-1726/20/8/085010. PMC 3176498 . PMID  21949469. 
  18. ^ La estructura abierta de una masa que ha leudado demasiado es fácil de observar: en lugar de consistir en burbujas de gas discretas, la masa consiste en un espacio de gas lleno de hilos de la pasta de harina y agua. [ investigación original? ] [ cita requerida ]
  19. ^ Wang, Shuo; Austin, Pedro; Chakrabati-Bell, Sumana (2011). "Es un laberinto: la estructura de los poros del pan rallado". Revista de ciencia de los cereales . 54 (2): 203–210. doi :10.1016/j.jcs.2011.05.004.
  20. ^ "Nueva arma en la guerra contra la gripe aviar: pequeñas burbujas". NBC News . 10 de junio de 2007 . Consultado el 21 de enero de 2024 .
  21. ^ Benson, ER; Alphin, RL; Dawson, MD; Malone, GW (mayo de 2009). "Uso de espuma a base de agua para despoblar patos y otras especies". Ciencia avícola . 88 (5): 904–910. doi :10.3382/ps.2008-00268. PMID  19359675.
  22. ^ Bolotnikova, Marina (8 de marzo de 2022). «'Los están cocinando vivos': llamamientos a prohibir los métodos de matanza 'crueles' en las granjas estadounidenses». The Guardian . ISSN  0261-3077 . Consultado el 21 de enero de 2024 .
  23. ^ ab Gibson, Ashby (1999). Sólidos celulares: estructura y propiedades . Cambridge, Reino Unido: Cambridge University Press. ISBN 9781316025420.
  24. ^ Carroll, Gregory T.; Kirschman, David L. (23 de enero de 2023). "La unidad de filtración catalítica de humo quirúrgico reduce los niveles de formaldehído en un entorno de quirófano simulado". ACS Chemical Health & Safety . 30 (1): 21–28. doi :10.1021/acs.chas.2c00071. ISSN  1871-5532. S2CID  255047115.
  25. ^ Wu, Qiong; Andersson, Richard L.; Holgate, Tim; Johansson, Eva; Gedde, Ulf W.; Olsson, Richard T.; Hedenqvist, Mikael S. (2014). "Bioespumas ignífugas altamente porosas y sostenibles basadas en gluten de trigo y sílice polimerizada in situ". Journal of Materials Chemistry A . 2 (48). 20996–21009. doi : 10.1039/C4TA04787G .
  26. ^ Reyes-Labarta, JA; Marcilla, A. (2008). "Estudio cinético de las descomposiciones implicadas en la degradación térmica de la azodicarbonamida comercial". Journal of Applied Polymer Science . 107 (1): 339–346. doi :10.1002/app.26922. hdl : 10045/24682 .
  27. ^ Reyes-Labarta, JA; Marcilla, A. (2012). "Tratamiento térmico y degradación de espumas reticuladas de etileno acetato de vinilo-polietileno-azodicarbonamida-ZnO. Modelado y análisis cinético completo". Investigación en química industrial e ingeniería . 51 (28): 9515–9530. doi :10.1021/ie3006935.
  28. ^ Reyes-Labarta, JA; Marcilla, A. (2008). "Análisis de calorimetría diferencial de barrido del tratamiento térmico de mezclas ternarias de etileno acetato de vinilo, polietileno y azodicarbonamida". Journal of Applied Polymer Science . 110 (5): 3217–3224. doi :10.1002/app.28802. hdl : 10045/13312 .
  29. ^ Reyes-Labarta, JA; Olaya, MM; Marcilla, A. (2006). "Estudio DSC de las transiciones involucradas en el tratamiento térmico de mezclas espumables de copolímero PE y EVA con azodicarbonamida". Journal of Applied Polymer Science . 102 (3): 2015–2025. doi :10.1002/app.23969. hdl : 10045/24680 .
  30. ^ Ashida, Kaneyoshi (2006). Poliuretano y espumas relacionadas: química y tecnología. CRC Press. pp. 79–81. ISBN 978-1-58716-159-9. Archivado desde el original el 17 de febrero de 2017.

Lectura adicional

  • Weaire, D y Hutzler, S (1999). La física de las espumas. Oxford, Inglaterra: Oxford University Press. ISBN 0198510977. Consultado el 30 de agosto de 2024 .{{cite book}}: CS1 maint: multiple names: authors list (link)Un tratado moderno centrado casi exclusivamente en las espumas líquidas.
  • Gibson, LJ y Ashby, MF (1997). Sólidos celulares: estructura y propiedades. Cambridge Solid State Science. Cambridge, Inglaterra: Cambridge University Press. ISBN 0521499119. Consultado el 30 de agosto de 2024 .{{cite book}}: CS1 maint: multiple names: authors list (link)Un tratado calificado de clásico por Weaire y Hutzler (1999) sobre espumas sólidas y la razón por la que limitan su enfoque a las espumas líquidas.
  • Cantat, yo ; Cohen-Addad, S; Elías, F; Graner, F; Höhler, R; Pitois, O; Rouyer, F y Saint-Jalmes, A (2013). Espumas: Estructura y Dinámica. Oxford, Inglaterra: Oxford University Press. ISBN 978-0199662890. Consultado el 30 de agosto de 2024 .{{cite book}}: CS1 maint: multiple names: authors list (link) Tenga en cuenta que esta fuente también se centra en las espumas líquidas.
  • Thomas Hipke, Günther Lange, René Poss: Taschenbuch für Aluminiumschäume. Aluminium-Verlag, Düsseldorf 2007, ISBN 978-3-87017-285-5 . 
  • Hannelore Dittmar-Ilgen: Metalle lernen schwimmen. En: Dies.: Wie der Kork-Krümel ans Weinglas kommt. Hirzel, Stuttgart 2006, ISBN 978-3-7776-1440-3 , pág.74. 


Busque espuma en Wikcionario, el diccionario libre.
Wikimedia Commons alberga una categoría multimedia sobre Espuma .
  • Andrew M. Kraynik, Douglas A. Reinelt, Frank van Swol Estructura de espuma monodispersa aleatoria
  • Moriarty, Philip (2010). "Física de la espuma". Sixty Symbols . Brady Haran para la Universidad de Nottingham .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Foam&oldid=1247773599"