Curva de costos
En economía , una curva de costos es un gráfico de los costos de producción en función de la cantidad total producida. En una economía de libre mercado , las empresas productivamente eficientes optimizan su proceso de producción minimizando los costos de manera consistente con cada nivel posible de producción, y el resultado es una curva de costos. Las empresas que maximizan las ganancias usan las curvas de costos para decidir las cantidades de producción. Existen varios tipos de curvas de costos, todas relacionadas entre sí, incluidas las curvas de costos totales y promedio; las curvas de costos marginales ("por cada unidad adicional"), que son iguales al diferencial de las curvas de costos totales; y las curvas de costos variables. Algunas son aplicables al corto plazo , otras al largo plazo .
Notación
Existen siglas estándar para cada concepto de costo, expresadas en términos de los siguientes descriptores:
- SR = corto plazo (costos gastados en materiales no reutilizables, por ejemplo, materias primas)
- LR = largo plazo (costo gastado en materiales renovables, por ejemplo, equipos)
- A = promedio (por unidad de producción)
- M = marginal (para una unidad adicional de producción)
- F = fijo (no ajustable)
- V = variable (ajustable)
- T = total (fijo más variable)
- C = costo
Estos se pueden combinar de varias maneras para expresar diferentes conceptos de costo (a menudo se omiten SR y LR cuando el contexto es claro): uno del primer grupo (SR o LR); ninguno o uno del segundo grupo (A, M o ninguno (que significa “nivel”); ninguno o uno del tercer grupo (F, V o T); y el cuarto elemento (C).
De las diversas combinaciones tenemos las siguientes curvas de costos de corto plazo:
- Costo fijo promedio de corto plazo (SRAFC)
- Costo total promedio de corto plazo (SRAC o SRATC)
- Costo variable promedio de corto plazo (CVP o CVPA)
- Costo marginal de corto plazo (CMPR)
- Costo fijo de corto plazo (CF o SRFC)
- Costo total de corto plazo (SRTC)
- Costo variable de corto plazo (VC o SRVC)
y las siguientes curvas de costos de largo plazo :
- Coste total medio de largo plazo (LRAC o LRATC)
- Costo marginal de largo plazo (CMLR)
- Costo total de largo plazo (LRTC)
Curvas de costo total de corto plazo (SRTC) y de costo total de largo plazo (LRTC)

Las curvas de costo total de corto plazo (SRTC) y de costo total de largo plazo (LRTC) aumentan en la cantidad de producción producida porque producir más producción requiere un mayor uso de mano de obra tanto en el corto como en el largo plazo, y porque en el largo plazo producir más producción implica usar más capital físico; y usar más de cualquiera de los dos insumos implica incurrir en mayores costos de insumos.
En el corto plazo, con un único insumo variable (el uso de mano de obra), cada posible cantidad de producción requiere una cantidad específica de uso de mano de obra, y el costo total de corto plazo como función del nivel de producción es esta única cantidad de mano de obra multiplicada por el costo unitario de la mano de obra. Pero en el largo plazo, con las cantidades tanto de mano de obra como de capital físico que se pueden elegir, el costo total de producir un nivel de producción particular es el resultado de un problema de optimización: la suma de los gastos en mano de obra (la tasa salarial multiplicada por el nivel elegido de uso de mano de obra) y los gastos en capital (el costo unitario del capital multiplicado por el nivel elegido de uso de capital físico) se minimiza con respecto al uso de mano de obra y al uso de capital, sujeto a la igualdad de la función de producción que relaciona la producción con ambos usos de insumos; entonces, el nivel (mínimo) de costo total es el costo total de producir la cantidad dada de producción.
Curvas de costos variables y fijos de corto plazo (SRVC y SRFC o VC y FC)
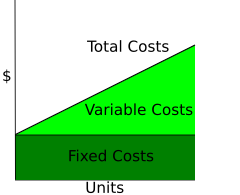
Como el costo fijo de corto plazo (CF/CFPR) no varía con el nivel de producción, su curva es horizontal, como se muestra aquí. Los costos variables de corto plazo (VC/VCPR) aumentan con el nivel de producción, ya que cuanto mayor es la producción, mayor es la cantidad de insumos variables que se deben utilizar y pagar.
Curva de costo variable promedio de corto plazo (CVP o CVRPA)

El costo variable promedio (CVP/CVPA) (que es un concepto de corto plazo) es el costo variable (típicamente el costo laboral) por unidad de producción: CVPA = wL / Q donde w es el salario, L es la cantidad de trabajo utilizada y Q es la cantidad de producción producida. La curva CVPA traza el costo variable promedio de corto plazo en relación con el nivel de producción y generalmente tiene forma de U. Sin embargo, si bien esto es conveniente para la teoría económica, se ha argumentado que tiene poca relación con el mundo real. Algunas estimaciones muestran que, al menos en el sector manufacturero, la proporción de empresas que informan una curva de costos en forma de U está en el rango del 5 al 11 por ciento. [1] [2]
Curva de costo fijo promedio de corto plazo (CFPCP)
Dado que el costo fijo por definición no varía con la producción, el costo fijo promedio de corto plazo (CPPCP) (es decir, el costo fijo de corto plazo por unidad de producción) es menor cuando la producción es mayor, lo que da lugar a la curva de pendiente descendente que se muestra.
Curvas de costo total promedio de corto y largo plazo (SRATC o SRAC y LRATC o LRAC)
La curva de costo total promedio se construye para capturar la relación entre el costo por unidad de producción y el nivel de producción , ceteris paribus . Una empresa perfectamente competitiva y productivamente eficiente organiza sus factores de producción de tal manera que el uso de los factores de producción sea lo más bajo posible, consistente con el nivel dado de producción que se va a producir. En el corto plazo , cuando al menos un factor de producción es fijo, esto ocurre en el nivel de producción en el que ha disfrutado de todas las posibles ganancias de costo promedio derivadas del aumento de la producción. Esto es en el punto mínimo en el diagrama anterior.
El costo total de corto plazo está dado por
- ,
donde P K es el precio unitario de uso del capital físico por unidad de tiempo, P L es el precio unitario de la mano de obra por unidad de tiempo (la tasa salarial), K es la cantidad de capital físico utilizado y L es la cantidad de mano de obra utilizada. De esto obtenemos el costo promedio de corto plazo, denotado como SATC o SRAC, como STC / Q:
- ,
donde es el producto medio del capital y es el producto medio del trabajo. [3] : 191
Dentro del gráfico anterior, la curva de Costo Fijo Promedio y la curva de Costo Variable Promedio no pueden comenzar con cero, ya que en cantidad cero estos valores no están definidos ya que implicaría dividir por cero.
El costo promedio de corto plazo (SRATC/SRAC) es igual a los costos fijos promedio más los costos variables promedio. El costo fijo promedio cae continuamente a medida que aumenta la producción en el corto plazo, porque K es fijo en el corto plazo. La forma de la curva de costo variable promedio está determinada directamente por los rendimientos marginales crecientes y luego decrecientes del insumo variable (tradicionalmente, el trabajo). [4] : 210
La curva de costo promedio de largo plazo (LRATC/LRAC) es similar a la curva de corto plazo, pero permite que el uso del capital físico varíe.
Curva de costo marginal de corto plazo (CRPM)

Una curva de costo marginal de corto plazo (SRMC) representa gráficamente la relación entre el costo marginal (es decir, incremental) incurrido por una empresa en la producción de corto plazo de un bien o servicio y la cantidad de producción producida. Esta curva se construye para capturar la relación entre el costo marginal y el nivel de producción, manteniendo constantes otras variables, como la tecnología y los precios de los recursos. La curva de costo marginal generalmente tiene forma de U. El costo marginal es relativamente alto en pequeñas cantidades de producción; luego, a medida que aumenta la producción, el costo marginal disminuye, alcanza un valor mínimo y luego aumenta. El costo marginal se muestra en relación con el ingreso marginal (IM), la cantidad incremental de ingresos por ventas que una unidad adicional del producto o servicio traerá a la empresa. Esta forma de la curva de costo marginal es directamente atribuible a rendimientos marginales crecientes y luego decrecientes (y la ley de rendimientos marginales decrecientes ). El costo marginal es igual a w/MP L . [3] : 191 Para la mayoría de los procesos de producción, el producto marginal del trabajo inicialmente aumenta, alcanza un valor máximo y luego cae continuamente a medida que aumenta la producción. Así, el coste marginal cae inicialmente, alcanza un valor mínimo y luego aumenta. [4] : 209 La curva de coste marginal intersecta tanto la curva de coste variable medio como la curva de coste total medio (de corto plazo) en sus puntos mínimos. Cuando la curva de coste marginal está por encima de una curva de coste medio, la curva media está subiendo. Cuando la curva de costes marginales está por debajo de una curva media, la curva media está bajando. Esta relación se mantiene independientemente de si la curva marginal está subiendo o bajando. [5] : 226
Curva de costo marginal de largo plazo (CMLR)
La curva de costo marginal de largo plazo (LRMC) muestra para cada unidad de producción el costo total agregado incurrido en el largo plazo , es decir, el período conceptual en el que todos los factores de producción son variables. Dicho de otro modo, LRMC es el aumento mínimo en el costo total asociado con un aumento de una unidad de producción cuando todos los insumos son variables. [6]
La curva de costo marginal de largo plazo está determinada por los rendimientos a escala , un concepto de largo plazo, en lugar de la ley de rendimientos marginales decrecientes , que es un concepto de corto plazo. La curva de costo marginal de largo plazo tiende a ser más plana que su contraparte de corto plazo debido a una mayor flexibilidad de insumos. La curva de costo marginal de largo plazo interseca la curva de costo promedio de largo plazo en el punto mínimo de esta última. [3] : 208 Cuando el costo marginal de largo plazo está por debajo del costo promedio de largo plazo, el costo promedio de largo plazo está cayendo (ya que se consideran unidades adicionales de producción). [3] : 207 Cuando el costo marginal de largo plazo está por encima del costo promedio de largo plazo, el costo promedio está aumentando. El costo marginal de largo plazo es igual al costo marginal de corto plazo en el nivel de producción de menor costo promedio de largo plazo. LRMC es la pendiente de la función de costo total LR.
Graficar curvas de costos junto con curvas de ingresos
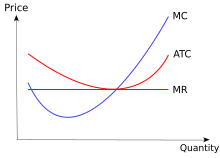
Las curvas de costos se pueden combinar para brindar información sobre las empresas. En este diagrama, por ejemplo, se supone que las empresas se encuentran en un mercado perfectamente competitivo . En un mercado perfectamente competitivo, el precio que las empresas enfrentan en el largo plazo sería el precio al cual la curva de costo marginal corta la curva de costo promedio, ya que cualquier precio por encima o por debajo de ese resultaría en la entrada o salida de la industria, llevando el precio determinado por el mercado al nivel que da un beneficio económico cero .
Curvas de costos y funciones de producción
Suponiendo que los precios de los factores son constantes, la función de producción determina todas las funciones de costos. [4] La curva de costo variable es el precio constante del insumo variable multiplicado por la función de producción de corto plazo invertida o la curva de producto total, y su comportamiento y propiedades están determinados por la función de producción. [3] : 209 [nb 1] Debido a que la función de producción determina la función de costo variable, necesariamente determina la forma y las propiedades de la curva de costo marginal y las curvas de costo promedio. [4]
Si la empresa es un competidor perfecto en todos los mercados de insumos y, por lo tanto, los precios unitarios de todos sus insumos no se ven afectados por la cantidad de insumos que compra la empresa, entonces se puede demostrar que en un nivel particular de producción, la empresa tiene economías de escala (es decir, está operando en una región de pendiente descendente de la curva de costo promedio de largo plazo) si y solo si tiene rendimientos crecientes a escala . [7] [8] [9] Del mismo modo, tiene deseconomías de escala (está operando en una región de pendiente ascendente de la curva de costo promedio de largo plazo) si y solo si tiene rendimientos decrecientes a escala, y no tiene ni economías ni deseconomías de escala si tiene rendimientos constantes a escala. En este caso, con competencia perfecta en el mercado de producción, el equilibrio del mercado de largo plazo involucrará a todas las empresas operando en el punto mínimo de sus curvas de costo promedio de largo plazo (es decir, en el límite entre economías y deseconomías de escala).
Sin embargo, si la empresa no es un competidor perfecto en los mercados de insumos, las conclusiones anteriores se modifican. Por ejemplo, si hay rendimientos crecientes a escala en un rango de niveles de producción, pero la empresa es tan grande en uno o más mercados de insumos que aumentar sus compras de un insumo eleva el costo unitario del insumo, entonces la empresa podría tener deseconomías de escala en ese rango de niveles de producción. Por otro lado, si la empresa puede obtener descuentos por volumen de un insumo, entonces podría tener economías de escala en un rango de niveles de producción incluso si tiene rendimientos decrecientes en la producción en ese rango de producción.
Relación entre diferentes curvas
- Costo total = Costos fijos (CF) + Costos variables (CV) = Costo total promedio (CTP) x Cantidad (C)
- Coste marginal (CM) = dC/dQ; CM es igual a la pendiente de la función de coste total y de la función de coste variable
- Costo total promedio (CTP) = Costo total/Q
- Coste fijo medio (CFP) = CF/Q
- Coste Variable Promedio (CVP) = VC/Q.
- CTA = CFA + CVA
- En un nivel de Q en el que la curva de CM está por encima de la curva de costo total promedio o de la curva de costo variable promedio, esta última curva está aumentando. [10] : 212
- Si el CM está por debajo del coste total promedio o del coste variable promedio, entonces la última curva está cayendo.
- Si CM es igual al coste total promedio, entonces el coste total promedio está en su valor mínimo.
- Si CM es igual al costo variable promedio, entonces el costo variable promedio está en su valor mínimo.
Relación entre las curvas de costos de corto y largo plazo
Para cada cantidad de producción existe un nivel de capital que minimiza los costos y una única curva de costo promedio de corto plazo asociada con la producción de la cantidad dada. [11] Las siguientes afirmaciones suponen que la empresa está utilizando el nivel óptimo de capital para la cantidad producida. De no ser así, la curva SRAC se encontraría "totalmente por encima" de la LRAC y no sería tangente en ningún punto.
- Cada curva STC puede ser tangente a la curva LRTC en un solo punto. La curva STC no puede cruzar (intersecar) la curva LRTC. [4] : 230 [10] : 228–229 La curva STC puede estar completamente “por encima” de la curva LRTC sin ningún punto de tangencia. [12] : 256
- Una curva STC es tangente a LRTC en el nivel de producción que minimiza los costos a largo plazo. En el punto de tangencia LRTC = STC. En todos los demás niveles de producción, STC superará a LRTC. [13] : 292–299
- Las funciones de costo promedio son la función de costo total dividida por el nivel de producción. Por lo tanto, la curva SATC también es tangente a la curva LRATC en el nivel de producción que minimiza el costo. En el punto de tangencia LRATC = SATC. En todos los demás niveles de producción SATC > LRATC [13] : 292–299 A la izquierda del punto de tangencia, la empresa está utilizando demasiado capital y los costos fijos son demasiado altos. A la derecha del punto de tangencia, la empresa está utilizando muy poco capital y los rendimientos decrecientes de la mano de obra están haciendo que los costos aumenten. [14]
- La pendiente de las curvas de costo total es igual al costo marginal. Por lo tanto, cuando el costo total de la producción es tangente al costo marginal de la producción, el costo total de la producción es igual al costo marginal de la producción.
- En el nivel de producción que minimiza los costos a largo plazo, LRTC = STC; LRATC = SATC y LRMC = SMC. [13] : 292–299
- El nivel de producción que minimiza los costos a largo plazo puede ser diferente del SATC mínimo. [10] : 229 [15] : 186
- Con costos unitarios fijos de los insumos, si la función de producción tiene rendimientos constantes a escala, entonces en el nivel mínimo de la curva SATC tenemos SATC = LRATC = SMC = LRMC. [13] : 292–299
- Con costos unitarios fijos de los insumos, si la función de producción tiene rendimientos crecientes a escala, el mínimo de la curva SATC está a la derecha del punto de tangencia entre las curvas LRAC y SATC. [13] : 292–299 Donde LRTC = STC, LRATC = SATC y LRMC = SMC.
- Con costos unitarios fijos de insumos y rendimientos decrecientes, el mínimo de la curva SATC está a la izquierda del punto de tangencia entre LRAC y SATC, [13] : 292–299 donde LRTC = STC, LRATC = SATC y LRMC = SMC.
- Con costos unitarios de insumos fijos, una empresa que experimenta rendimientos crecientes (decrecientes) a escala y está produciendo a su SAC mínimo siempre puede reducir el costo promedio en el largo plazo al expandir (reducir) el uso del insumo fijo. [13] : 292–99 [15] : 186
- LRATC siempre será igual o menor que SATC. [3] : 211
- Si el proceso de producción exhibe rendimientos constantes a escala, entonces el SRAC mínimo es igual al costo promedio de largo plazo mínimo. El LRAC y el SRAC se intersecan en sus valores mínimos comunes. Por lo tanto, con rendimientos constantes a escala, SRMC = LRMC = LRAC = SRAC.
- Si el proceso de producción experimenta un aumento o una disminución, el costo promedio mínimo de corto plazo no es igual al costo promedio mínimo de largo plazo. Si existen rendimientos crecientes a escala, el mínimo de largo plazo se producirá a un nivel de producción inferior al de los rendimientos de escala de escala. Esto se debe a que existen economías de escala que no se han explotado, por lo que, a largo plazo, una empresa siempre podría producir una cantidad a un precio inferior al costo promedio mínimo de corto plazo simplemente utilizando una planta más grande. [16]
- Con rendimientos decrecientes, el SRAC mínimo ocurre en un nivel de producción más bajo que el LRAC mínimo porque una empresa podría reducir los costos promedio simplemente disminuyendo el tamaño de sus operaciones.
- El mínimo de una SRAC ocurre cuando la pendiente es cero. [17] Por lo tanto, los puntos de tangencia entre la curva LRAC en forma de U y el mínimo de la curva SRAC coincidirían solo con la porción de la curva LRAC que exhibe economías de escala constantes. Para que los rendimientos crecientes sean de escala, el punto de tangencia entre la LRAC y la SRAC tendría que ocurrir en un nivel de producción por debajo del nivel asociado con el mínimo de la curva SRAC.
Curvas en forma de U
Tanto la curva SRAC como la LRAC se expresan típicamente en forma de U. [10] : 211, 226 [15] : 182, 187–188 Sin embargo, las formas de las curvas no se deben a los mismos factores. Para la curva de corto plazo, la pendiente descendente inicial se debe en gran medida a la disminución de los costos fijos promedio. [4] : 227 Los rendimientos crecientes del insumo variable a niveles bajos de producción también juegan un papel, [18] mientras que la pendiente ascendente se debe a los rendimientos marginales decrecientes del insumo variable. [4] : 227 Con la curva de largo plazo, la forma, por definición, refleja economías y deseconomías de escala. [15] : 186 En niveles bajos de producción, las funciones de producción de largo plazo generalmente exhiben rendimientos crecientes a escala, lo que, para las empresas que son competidoras perfectas en los mercados de insumos, significa que el costo promedio de largo plazo está cayendo; [4] : 227 la pendiente ascendente de la función de costo promedio de largo plazo en niveles más altos de producción se debe a rendimientos decrecientes a escala en esos niveles de producción. [4] : 227
Forma empírica de las curvas de costo promedio
Hay algunas evidencias que demuestran que las curvas de costo promedio no suelen tener forma de U. En una encuesta realizada por Wilford J. Eiteman y Glenn E. Guthrie en 1952, se mostró a los gerentes de 334 empresas varias curvas de costos diferentes y se les pidió que especificaran cuál representaba mejor la curva de costos de la empresa. El 95% de los gerentes que respondieron a la encuesta informaron curvas de costos con costos constantes o decrecientes. [1]
Alan Blinder , ex vicepresidente de la Asociación Estadounidense de Economía , realizó el mismo tipo de encuesta en 1998, en la que participaron 200 empresas estadounidenses en una muestra que debería ser representativa de la economía estadounidense en general. Encontró que aproximadamente el 40% de las empresas informaron de una caída de los costos variables o marginales, y el 48,4% informaron de costos marginales/variables constantes. [19]
Véase también
Notas
- ^ La pendiente de la función de producción de corto plazo es igual al producto marginal del insumo variable, convencionalmente el trabajo. La pendiente de la función de costo variable es el costo marginal. La relación entre el CM y el producto marginal del trabajo MP L es CM = w/MP L . Debido a que se supone que la tasa salarial w es constante, la forma de la curva de costo variable depende completamente del producto marginal del trabajo. La curva de costo total de corto plazo es simplemente la curva de costo variable más los costos fijos.
Referencias
- ^ ab Eiteman, Wilford J.; Guthrie, Glenn E. (1952). "La forma de la curva de costo promedio". American Economic Review . 42 (5): 832–838. JSTOR 1812530.
- ^ Blinder AS, Canetti E, Lebow D y Rudd J (1998) Preguntar sobre precios: un nuevo enfoque para entender la rigidez de los precios, Nueva York: Russell Sage Foundation.
- ^ abcdef Perloff, J. Microeconomía , 5.ª ed. Pearson, 2009.
- ^ abcdefghi Perloff, J., 2008, Microeconomía: teoría y aplicaciones con cálculo , Pearson. ISBN 978-0-321-27794-7
- ^ Lipsey, Richard G. (1975). Introducción a la economía positiva (cuarta edición). Weidenfeld & Nicolson. Págs. 57-8. ISBN 978-0-297-76899-9.
- ^ Sexton, Robert L.; Graves, Philip E.; Lee, Dwight R. (1993). "La curva de costo marginal de corto y largo plazo: una nota pedagógica" (PDF) . Revista de Educación Económica . 24 (1): 34–37. doi :10.1080/00220485.1993.10844777.
- ^ Gelles, Gregory M.; Mitchell, Douglas W. (1996). "Retornos a escala y economías de escala: observaciones adicionales". Revista de educación económica . 27 (3): 259–261. doi :10.1080/00220485.1996.10844915.
- ^ Frisch, R., Teoría de la producción , Drodrecht: D. Reidel, 1965.
- ^ Ferguson, CE, La teoría neoclásica de la producción y la distribución , Londres: Cambridge Univ. Press, 1969.
- ^ abcd Pindyck, R., y Rubinfeld, D., Microeconomía , 5.ª ed., Prentice-Hall, 2001.
- ^ Nicholson: Teoría microeconómica 9.ª ed. Página 238 Thomson 2005
- ^ Kreps, D., Un curso de teoría microeconómica , Princeton Univ. Press, 1990.
- ^ abcdefg Binger, B., y Hoffman, E., Microeconomía con cálculo , 2.ª ed., Addison-Wesley, 1998.
- ^ Frank, R., Microeconomía y comportamiento 7.ª ed. (Mc-Graw-Hill) ISBN 978-0-07-126349-8 en 321.
- ^ abcd Melvin y Boyes, Microeconomía , 5.ª ed., Houghton Mifflin, 2002
- ^ Perloff, J. Teoría y aplicación de la microeconomía con cálculo Pearson (2008) pág. 231.
- ^ Nicholson: Teoría microeconómica 9.ª ed. Página Thomson 2005
- ^ Boyes, W., La nueva economía gerencial , Houghton Mifflin, 2004.
- ^ Alan Stuart Blinder, Preguntar por los precios: un nuevo enfoque para entender la rigidez de los precios , Russell Sage Foundation, Nueva York, 1998





