Vibración de cuerdas

La vibración de una cuerda es una onda . La resonancia hace que una cuerda vibrante produzca un sonido con una frecuencia constante , es decir, un tono constante . Si la longitud o la tensión de la cuerda se ajustan correctamente, el sonido producido es un tono musical . Las cuerdas vibrantes son la base de los instrumentos de cuerda, como las guitarras , los violonchelos y los pianos .

La velocidad de propagación de una onda en una cuerda ( ) es proporcional a la raíz cuadrada de la fuerza de tensión de la cuerda ( ) e inversamente proporcional a la raíz cuadrada de la densidad lineal ( ) de la cuerda:${\estilo de visualización v}$${\estilo de visualización T}$${\estilo de visualización \mu}$

${\displaystyle v={\sqrt {T \sobre \mu }}.}$

Esta relación fue descubierta por Vincenzo Galilei a finales del siglo XVI. ^{[ cita requerida ]}

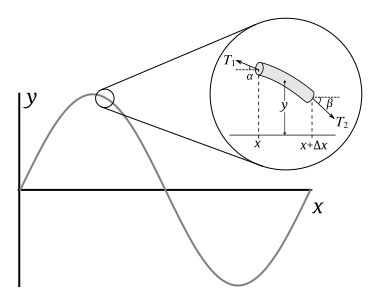
Fuente: ^[1]

Sea la longitud de un trozo de cuerda, su masa y su densidad lineal . Si los ángulos y son pequeños, entonces las componentes horizontales de la tensión en cada lado pueden aproximarse mediante una constante , para la cual la fuerza horizontal neta es cero. En consecuencia, utilizando la aproximación de ángulos pequeños, las tensiones horizontales que actúan en ambos lados del segmento de cuerda están dadas por${\displaystyle \Delta x}$${\estilo de visualización m}$${\estilo de visualización \mu}$${\estilo de visualización \alpha}$${\estilo de visualización \beta}$${\estilo de visualización T}$

${\displaystyle T_{1x}=T_{1}\cos(\alpha )\approx T.}$

${\displaystyle T_{2x}=T_{2}\cos(\beta )\approx T.}$

De la segunda ley de Newton para el componente vertical, la masa (que es el producto de su densidad lineal y su longitud) de esta pieza por su aceleración, , será igual a la fuerza neta sobre la pieza:${\estilo de visualización a}$

${\displaystyle \Sigma F_{y}=T_{1y}-T_{2y}=-T_{2}\sin(\beta )+T_{1}\sin(\alpha )=\Delta ma\approx \mu \Delta x{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Dividiendo esta expresión por y sustituyendo la primera y segunda ecuación se obtiene (podemos elegir la primera o la segunda ecuación para , por lo que elegimos convenientemente cada una con el ángulo correspondiente y )${\estilo de visualización T}$${\estilo de visualización T}$${\estilo de visualización \beta}$${\estilo de visualización \alpha}$

${\displaystyle -{\frac {T_{2}\sin(\beta )}{T_{2}\cos(\beta )}}+{\frac {T_{1}\sin(\alpha )}{T_{1}\cos(\alpha )}}=-\tan(\beta )+\tan(\alpha )={\frac {\mu \Delta x}{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Según la aproximación de ángulos pequeños, las tangentes de los ángulos en los extremos del trozo de cuerda son iguales a las pendientes en los extremos, con un signo menos adicional debido a la definición de y . Usando este hecho y reordenando se obtiene${\estilo de visualización \alpha}$${\estilo de visualización \beta}$

${\displaystyle {\frac {1}{\Delta x}}\left(\left.{\frac {\parcial y}{\parcial x}}\right|^{x+\Delta x}-\left.{\frac {\parcial y}{\parcial x}}\right|^{x}\right)={\frac {\mu }{T}}{\frac {\parcial ^{2}y}{\parcial t^{2}}}.}$

En el límite que tiende a cero, el lado izquierdo es la definición de la segunda derivada de :${\displaystyle \Delta x}$${\estilo de visualización y}$

${\displaystyle {\frac {\parcial ^{2}y}{\parcial x^{2}}}={\frac {\mu }{T}}{\frac {\parcial ^{2}y}{\parcial t^{2}}}.}$

Esta es la ecuación de onda para , y el coeficiente del segundo término derivado del tiempo es igual a ; por lo tanto${\displaystyle y(x,t)}$${\displaystyle {\frac {1}{v^{2}}}}$

${\displaystyle v={\sqrt {T \sobre \mu }},}$

Donde es la velocidad de propagación de la onda en la cuerda (ver el artículo sobre la ecuación de onda para más información sobre esto). Sin embargo, esta derivación solo es válida para vibraciones de pequeña amplitud; para las de gran amplitud, no es una buena aproximación para la longitud del trozo de cuerda, el componente horizontal de la tensión no es necesariamente constante. Las tensiones horizontales no se aproximan bien mediante .${\estilo de visualización v}$${\displaystyle \Delta x}$${\estilo de visualización T}$

Una vez conocida la velocidad de propagación, se puede calcular la frecuencia del sonido producido por la cuerda. La velocidad de propagación de una onda es igual a la longitud de onda dividida por el período o multiplicada por la frecuencia :${\estilo de visualización \lambda}$ ${\estilo de visualización \tau}$ ${\estilo de visualización f}$

${\displaystyle v={\frac {\lambda }{\tau }}=\lambda f.}$

Si la longitud de la cuerda es , el armónico fundamental es el producido por la vibración cuyos nodos son los dos extremos de la cuerda, por lo que es la mitad de la longitud de onda del armónico fundamental. De aquí se obtienen las leyes de Mersenne :${\estilo de visualización L}$${\estilo de visualización L}$

${\displaystyle f={\frac {v}{2L}}={1 \sobre 2L}{\sqrt {T \sobre \mu }}}$

donde es la tensión (en Newtons), es la densidad lineal (es decir, la masa por unidad de longitud), y es la longitud de la parte vibrante de la cuerda. Por lo tanto:${\estilo de visualización T}$${\estilo de visualización \mu}$${\estilo de visualización L}$

• Cuanto más corta sea la cuerda, más alta será la frecuencia de la fundamental.
• Cuanto mayor sea la tensión, mayor será la frecuencia de la fundamental.
• Cuanto más ligera sea la cuerda, más alta será la frecuencia fundamental.

Además, si tomamos el n-ésimo armónico como si tuviera una longitud de onda dada por , entonces obtenemos fácilmente una expresión para la frecuencia del n-ésimo armónico:${\displaystyle \lambda _{n}=2L/n}$

${\displaystyle f_{n}={\frac {nv}{2L}}}$

Y para una cuerda bajo una tensión T con densidad lineal , entonces${\estilo de visualización \mu}$

${\displaystyle f_{n}={\frac {n}{2L}}{\sqrt {\frac {T}{\mu }}}}$

Se pueden ver las formas de onda en una cuerda vibrante si la frecuencia es lo suficientemente baja y la cuerda vibrante se mantiene frente a una pantalla CRT como la de un televisor o una computadora ( no la de un osciloscopio analógico). Este efecto se llama efecto estroboscópico , y la velocidad a la que la cuerda parece vibrar es la diferencia entre la frecuencia de la cuerda y la frecuencia de actualización de la pantalla. Lo mismo puede suceder con una lámpara fluorescente , a una velocidad que es la diferencia entre la frecuencia de la cuerda y la frecuencia de la corriente alterna . (Si la frecuencia de actualización de la pantalla es igual a la frecuencia de la cuerda o un múltiplo entero de la misma, la cuerda aparecerá quieta pero deformada). A la luz del día y otras fuentes de luz no oscilantes, este efecto no ocurre y la cuerda aparece quieta pero más gruesa, y más clara o borrosa, debido a la persistencia de la visión .

Un efecto similar pero más controlable se puede obtener utilizando un estroboscopio . Este dispositivo permite hacer coincidir la frecuencia de la lámpara de destello de xenón con la frecuencia de vibración de la cuerda. En una habitación oscura, esto muestra claramente la forma de onda. De lo contrario, se puede utilizar la flexión o, quizás más fácilmente, ajustando las clavijas de la máquina, para obtener la misma, o un múltiplo, de la frecuencia de CA para lograr el mismo efecto. Por ejemplo, en el caso de una guitarra, la sexta cuerda (la más grave) presionada hasta el tercer traste da un sol a 97,999 Hz. Un ligero ajuste puede alterarlo a 100 Hz, exactamente una octava por encima de la frecuencia de corriente alterna en Europa y la mayoría de los países de África y Asia, 50 Hz. En la mayoría de los países de América, donde la frecuencia de CA es de 60 Hz, alterar la A# en la quinta cuerda, primer traste de 116,54 Hz a 120 Hz produce un efecto similar.

• Instrumentos con trastes
• Acústica musical
• Vibraciones de un tambor circular
• El experimento de Melde
• 3er puente (resonancia armónica basada en divisiones de cuerdas iguales)
• Resonancia de cuerdas
• Cambio de fase de reflexión

• Molteno, TCA; NB Tufillaro (septiembre de 2004). "Una investigación experimental sobre la dinámica de una cuerda". American Journal of Physics . 72 (9): 1157–1169. Bibcode :2004AmJPh..72.1157M. doi :10.1119/1.1764557.
• Tufillaro, NB (1989). "Vibraciones de cuerdas no lineales y caóticas". American Journal of Physics . 57 (5): 408. Bibcode :1989AmJPh..57..408T. doi :10.1119/1.16011.

Específico

• "La cuerda vibrante" de Alain Goriely y Mark Robertson-Tessi, The Wolfram Demonstrations Project .